[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 30, No. 2, pp.149-160

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Apr 2020

Received 31 Jan 2020 Revised 27 Feb 2020 Accepted 24 Mar 2020

DOI: https://doi.org/10.5050/KSNVE.2020.30.2.149

디지털 트윈을 사용한 구조 진동 가상 센서 시스템

오승인^* ; 박다은^* ; 백현우^* ; 김승훈^** ; 이재경^*** ; 김진균^*^{, †}

Virtual Sensing System of Structural Vibration using Digital Twin

Seungin Oh^* ; Daeun Park^* ; Hyunwoo Baek^* ; Seunghun Kim^** ; Jai-Kyung Lee^*** ; Jin-Gyun Kim^*^{, †}

*Member, Department of mechanical engineering, Kyung Hee University, Student
**Department of Astronomy & Space Science, Kyung Hee University, Student
***Korea Institute of Machinery & Materials, Principal Researcher

Correspondence to: ^†Member, Department of mechanical engineering, Kyung Hee University, Professor E-mail : jingyun.kim@khu.ac.kr # A part of this paper was presented at the KSNVE 2019 Annual Autumn Conference

‡ Recommended by Editor Jae Eun Kim

Abstract

Virtual sensing complements limited real-sensing information using a numerical (or analytical) model that is created with measured data. In this work, we propose a virtual-sensing system for structural vibration. Finite element model updating is employed to calibrate the numerical model to the real model and output modal information, including damping coefficients. A reduced-order modeling technique and a modified time integrator are also used to reduce the computational burden in the online sensing process and synchronize the numerical model to the real model, thereby creating a model-based digital twin. The proposed virtual sensing is tested by implementing it to solve a cantilever beam problem.

Keywords:

Structural Dynamics, Finite Element Model updating, Digital Twin, Virtual Sensing, Reduced-order Modeling

키워드:

구조동역학, 유한요소 모델 업데이팅, 디지털 트윈, 가상 센서, 축소모델링

1. 서 론

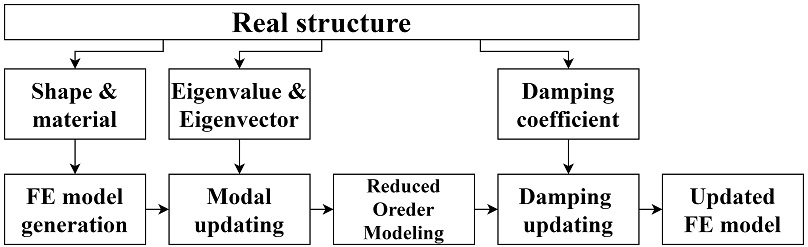
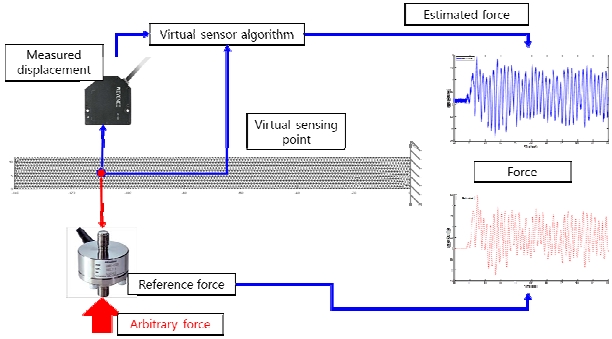
최근 정보통신 기술의 급격한 발전과 사물인터넷(internet on things, IOT)기술의 보편화에 따라, 기계시스템의 복잡도 또한 급증하고 있다. 특히, 기계시스템의 건전성을 실시간으로 추정하고 나아가 구조물의 수명을 사전에 예측해 선제적으로 대응하기 위한 고장예지 및 건전성 관리(prognostics and health monitoring, PHM) 기술에 대한 요구가 점차 심화되고 있다^(1,2). 한편, 반도체 기술의 급격한 성장은 컴퓨터의 소형화 및 연산속도의 고도화를 이루어 내었다. 이에 따라, 매우 저렴한 비용만으로 고성능의 소형 연산 시스템을 구성할 수 있는 시대가 되었다. 이러한 기술적 배경은 4차 산업혁명의 중요 기반기술의 하나인 디지털트윈(digital twin)기술의 원동력이 되고 있다^(3,4). Fig. 1은 디지털 트윈의 예를 보여준다. 디지털 트윈 시스템을 성공적으로 구성하기 위해서는, 실제 구조물의 상태를 물리 모델로 전달하기 위한 정밀 센서 기술이 반드시 요구된다. 그러나, 고정밀 데이터를 얻기 위한 다양한 센서의 활용은 비용의 증가를 가져올 수 있으며, 특히 구조진동 시스템에서의 센서 부착은 질량 및 강성에 직접적인 변화를 일으켜 측정 데이터의 신뢰성 감소를 유발하기도 한다. 또한 데이터의 유형 및 측정 위치에 따라 접근 및 측정이 불가능 해질 우려가 있다는 점도 기존 센싱 기술의 한계점으로 지목된다.

Fig. 1

Example of digital twin

이 연구에서는 이러한 한계를 극복하고자, 구조 진동 구조물의 응답 특성을 정확히 표현할 수 있는 모델 기반의 디지털 트윈을 활용하여 가상 센서 시스템(virtual sensor system)을 구성하였다. 이를 위해 먼저 구조진동 특성을 정확하게 표현할 수 있도록 유한요소모델 업데이팅(finite element model updating) 기술을 적용하였으며^(5~9,11), 연산시간 최소화 및 실제모델과 디지털 모델간의 실시간 연동을 위해 축소모델링(reduced-order modeling, ROM) 기술을 활용하였다^(10,14,15). 마지막으로 본 연구의 목적에 맞게 보정된 시간적분 알고리즘을 활용하여 직접 계측되지 않은 지점의 응답을 실시간으로 추정할 수 있는 가상 센서 시스템을 제안하였으며, 이를 단순 외팔보(cantilever) 문제에 적용하여 그 성능을 검증하였다.

2. 유한요소 모델링 및 보정

이 연구에서는 실제 구조물의 구조진동 특성을 모사하기 위하여 유한요소 모델을 사용하였다. 따라서 제시된 구조진동 가상 센서 시스템의 정확도를 높이기 위해서는 구축된 유한요소 모델의 신뢰도를 우선적으로 확보할 필요가 있다. 이를 위해 이 연구에서는 기본적인 물성정보와 기하학적 정보를 바탕으로 유한요소 모델을 구축하고, 실제 구조물의 실험 결과를 기반으로 하여 이를 업데이트하였다.

일반적인 구조진동 계의 유한요소 모델은 식 (1)과 같은 수식으로 표현된다.

M u ¨ + C u ˙ + K u = f

(1)

이때 M, C, K 는 각각 질량, 감쇠, 강성 행렬을 나타내며 u 와 f 는 변위와 외력을 나타낸다. 일반적 Fig. 1인 방법으로 구축된 유한요소 모델은 구조물 설계 시 사용된 목표 물성 및 형상을 기반으로 한다. 따라서, 이는 제조 공차, 사용 재료의 불확실성 등으로 인해 실제 모델과 다소간의 차이를 보일 수 있으며, 수치모델의 신뢰성 확보를 위해 이의 보정기술이 요구된다.

이 연구에서는 유한요소 모델의 보정을 위해 정량화된 기준에 의해 특성 오차를 검증하였으며, 복합적인 모델 업데이트 기법을 적용하여 오차를 최소화하였다. 모델 업데이트 과정은 Fig. 2에 표기된 절차에 따라 수행되었다. 업데이트 기법 및 절차는 효율성 및 신뢰성 향상을 목적으로 계획되었다. 특히 수치모델과 실제모델간의 동기화 및 빠른 계산속도 구현을 위해 모델 차수 축소 기법이 활용되었다. 형상 및 밀도 등 직접 측정이 가능한 물리량은 이 절에 소개된 업데이트 기법의 적용 전 보정을 완료하였다.

Fig. 2

FEM model updating process

2.1 모달 정보 업데이트

고유진동수(natural frequency) 및 모드형상(mode shape)은 수학적으로 고유값(eigenvalue), 고유벡터(eigenvector)로 정의될 수 있으며, 이는 구조진동 특성의 정량화를 위해 널리 사용된다. 이 연구에서는 유한요소 모델의 고유진동수 및 고유벡터 간의 오차 최소화를 일차적으로 수행하였다. 이때 식 (1)의 운동방정식은 식 (2)와 같이 무감쇠 시스템으로 단순화하여 질량 및 강성행렬을 보정하였으며, 추후 업데이트 과정에 의해 감쇠행렬을 추가하였다.

M u ¨ + K u = f

(2)

무감쇠 진동계에서 임의 차수 i 의 고유진동수 및 고유벡터는 식 (3)과 같은 고유치 문제를 통해 정의된다.

K φ i = λ i M φ i

(3)

여기에서 λ_i 와 φ_i 는 고유진동수와 고유벡터를 나타내며, 하첨자 i는 모드의 차수를 의미한다. 이때 실험 계측된 고유진동수와 유한요소 모델에서 계산된 고유진동수간의 오차는 식 (4)와 같이 나타낼 수 있다⁽⁵⁾.

λ i t = λ i a + λ i ε

(4)

이때 상첨자 t와 a는 각각 실험계측치, 유한요소 모델 연산치를 의미하며, ε는 두 값의 오차를 나타낸다.

고유진동수 오차를 임의의 변수와 변수 변화에 대한 테일러 1차 다항식으로 표현하면 식 (5)와 같이 표현할 수 있다.

λ i t = λ i a + ∂ λ i a ∂ θ ⋅ ∆ θ

(5)

이때 θ는 업데이트 하려는 임의의 변수를 의미한다. 따라서, 고유진동수의 임의 변수 2에 대한 1차 미분항 연산이 가능하다면 실제 구조물과 유한요소 모델의 고유진동수 차이를 최소화할 수 있는 방향으로 특정 변수를 변화시킬 수 있다. 식 (3)을 임의 변수에 대해 편미분한 후 고유진동수에 대해 정리하면 다음과 같은 관계식이 얻어진다^(6~8).

∂ λ i ∂ θ = φ i T ∂ K ∂ θ - λ i ∂ M ∂ θ φ i

(6)

식 (6)을 식 (5)에 대입하여 정리하면 고유진동수 오차를 최소화 하기 위한 특정 변수 변화량은 식 (7)과 같이 얻어질 수 있다.

∆ θ = λ i t - λ i a φ i T ∂ K ∂ θ - λ i ∂ M ∂ θ φ i

(7)

이를 식 (2)에 활용하면 특정 변수의 변화량을 고려한 보정된 운동 방정식은 식 (8)과 같이 표현할 수 있다.

M ¯ u ¨ + K ¯ u = f

(8a)

M ¯ = M + ∂ M ∂ θ ∆ θ

(8b)

K ¯ = K + ∂ K ∂ θ ∆ θ

(8c)

실험 계측된 고유벡터와 유한요소 모델에서 계산된 고유벡터간의 오차를 정량화하기 위하여 MAC(modal assurance criterion) 값을 도입하였다⁽⁹⁾.

M A C = φ i t ⋅ φ ¯ j a φ i t φ ¯ j a

(9)

2.2 유한요소 모델 축소법

위 과정을 통해 보정된 유한요소 모델은 실제 모델과 비교해 우수한 진동 정합성을 가질 수 있다. 그러나 이를 가상 센서 시스템에 활용하기 위해서는 상당한 연산량이 필요하다는 문제점이 있다. 이는 고려대상 구조진동 모델의 규모 및 요구되는 신뢰도 증가에 따라 고성능 연산장치를 요구하는 문제점을 발생시킨다.

이 연구에서는 실시간성을 극대화하기 위하여 적은 비용으로 비교적 높은 신뢰성을 갖는 모델을 구성하고자 축소모델링 기법을 적용하였다. 이를 위해 다양한 축소모델링 기법 중 널리 활용되고 있는 Craig-Bampton(CB) 기법⁽¹⁰⁾의 수식을 일부 변형하여 활용하였다. CB 기법은 제한된 수의 고유모드를 활용하여 효과적으로 모델의 축소가 가능하여 구조동역학 분야에서 널리 활용되고 있다. 특히, CB기법을 활용할 경우 모델의 축소 후에도 일부 물리자유도(degrees of freedom, DOFs)가 보존되므로, 실제 계측된 변형 데이터와의 직접 비교가 가능하다는 이점이 있다.

이 연구에서는 이러한 CB 기법의 특징을 활용하여 실제 센서의 위치를 물리량이 보존되는 자유도에 포함하였으며, 이를 통해 수치모델과 실제모델 간의 동기화를 가능하게 하였다. 그러나 부분구조합성법(component mode synthesis, CMS)의 대표적인 형태인 CB 기법은 내부자유도를 다수의 부분구조(substructure)로 분할하여 계산시간 최소화와 모델링 효율성 극대화를 추구한다. 따라서, 이 연구에서 활용한 정식은 부구조법을 적용하지 않았다는 점에서 CB 기법과 정확하게 일치하지 않으며, 오히려 자유도 기반축소모델링 기법인 Guyan 기법⁽¹⁴⁾과 CB 기법의 모드기반 축소모델링을 부구조법 없이 혼용한 형태로 보는 것이 타당하다⁽¹⁵⁾.

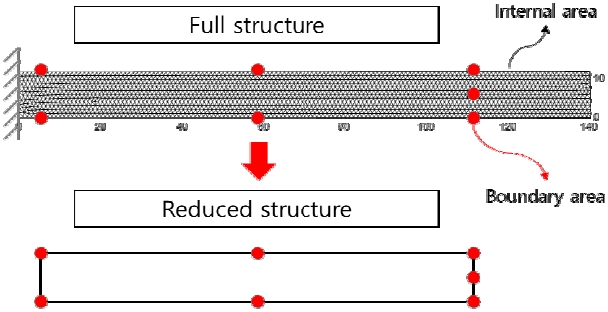
축소모델링에서 전체 자유도 중 물리량이 보존되는 자유도를 경계자유도(boundary DOFs), 그 이외의 자유도를 내부자유도(internal DOFs)로 정의할 수 있다. 이를 고려하면 식 (8)은 식 (10)과 같이 표현된다.

M s M c M c M b u ¨ s u ¨ b + K s K c K c K b u s u b = 0 f b

(10)

하첨자 s, b는 내부자유도와 경계자유도, 하첨자 c는 coupling 자유도를 의미한다. 유한요소모델의 전체 자유도 수를 N 으로 정의할 때 경계자유도의 수는 N_b, 내부자유도 수는 N_s로 정의할 수 있다.

전통적인 축소모델링에서는 내부자유도를 고유치 계산을 통해 얻은 주요한 모드(dominant mode)만을 활용해 근사하는 기법을 활용하는 것이 일반적이다. 내부자유도의 고유치 문제 행렬식은 식 (11)과 같이 정의한다.

K s Ψ i = λ i M s Ψ i

(11)

CB 기법에서는 식 (11)에서 계산한 매우 적은 수의 주요 모드에 추가적으로 정적거동을 가정하여 계산된 구속모드(consraint modes)를 활용하여 식 (12)와 같이 변위벡터를 근사한다.

u s u b = T^u^, u^= q d u b, T^= Ψ d - K s - 1 K c 0 I

(12)

이때 $T^$ 은 변환행렬(Transformation matrix), Ψ_d 는 주요모드로 구성된 행렬, q_d 는 이의 모달좌표계 벡터를 의미한다.

식 (12)를 식 (10)의 운동방정식에 적용하면 식 (13)과 같이 축소된 운동방정식을 얻을 수 있다.

M^u^¨ + K^u^= f^

(13a)

M^= T^T M ¯ T^

(13b)

K^= T^T K ¯ T^

(13c)

f^= T^T f

(13d)

식 (13)에서 활용한 주요 고유모드의 수를 N_d 로 가정하면 축소된 운동방정식의 자유도는 N_d + N_b로 정의할 수 있다. 일반적인 축소모델의 자유도는 전체 자유도의 5 % 내외이며, 특히 이 연구에서 경계자유도를 센서 측정 지점을 중심으로 정의하여 축소모델의 자유도를 전체자유도 대비 1 % 내외로 선정할 수 있게 하였다.

2.3 감쇠 특성 업데이트

외력에 의해 가진된 구조진동 구조물의 응답을 정확하게 모사하기 위해서는 감쇠계수에 대한 명확한 고려가 필수적이다. 그러나, 실제 실험에서 취득할 수 있는 감쇠계수는 매우 한정적이다. 따라서, 이 연구에서는 차수 축소 후의 운동방정식을 기반으로 감쇠계수 업데이트를 적용하였다. 이때 실험을 통해 측정된 감쇠계수를 사용하여 모달 영역의 감쇠계수를 업데이트 하였으며, 측정 불가능한 고차 영역에서의 감쇠계수는 1 % 감쇠 계수를 사용하여 업데이트 하였다. 이 연구에서는 아래의 주파수응답함수(frequency response function, FRF)를 사용하여 감쇠계수 업데이트 후 응답특성 변화를 검증하였다.

α k l ω = u k ω F l ω ≅ ∑ i = 1 N e i g φ i k φ i l λ i 2 - ω 2 + 2 j ω λ i ξ i

(14)

여기에서 α 는 주파수응답함수, ω는 구조물에 가해진 가진 하중 주파수를 의미하며, ξ는 감쇠계수를 의미한다. 하첨자 l, k 는 각각 모달실험에서 하중 작용지점과 응답 측정 지점을 의미한다. 실제 구조물의 감쇠 특성 및 고유진동수, 고유벡터는 충격해머 실험을 통해 계측 가능하다. 실험을 통해 얻어진 고유진동수, 고유벡터 및 감쇠계수를 사용하여 주파수 응답함수 계산이 가능하며, 유한요소 모델에서 얻어진 값과 비교하여 유사성을 정량화 할 수 있다. 이를 통해 보정된 유한요소 모델과 실제 구조물의 주파수 응답특성은 FRAC(frequency response assurance criterion)⁽¹¹⁾ 값을 사용하여 검증하였다.

F R A C = α k l t ⋅ α k l a α k l t α k l a

(15)

이 연구에서 활용한 유한요소 모델 업데이팅 검증기준(고유값 상대오차, MAC, FRF, FRAC 등)은 NASA(National Aeronautics and Space Administration), ECSS(European Cooperation for Space Standardization) 등에서 요구하는 수준에 부합하며, 이를 통해 가상 센서 시스템의 정밀도를 확보하였다⁽⁸⁾.

이 연구에서는 시간적분 과정에 물리영역의 운동방정식을 사용하고 있으므로, 구성된 모달 영역(주파수 영역(frequency domain)에서의 감쇠 행렬을 물리영역으로 전환해야 한다. 이를 위해 식 (16)과 같이 고유벡터의 질량에 대한 정규직교(orthonormal)성을 활용하였다⁽⁵⁾.

Φ^Φ^T = M^- 1

(16a)

M^Φ^Φ^T = Φ^Φ^T M^= I

(16b)

구조물의 모드영역 감쇠 행렬(C_modal)과 식 (13)에 추가되어야 할 감쇠 행렬( $C^$ )의 관계는 다음과 같이 표현할 수 있다⁽¹²⁾.

Φ^T C^Φ^= C m o d a l

(17)

식 (16)과 식 (17)을 사용하면 $C^$ 을 아래와 같이 계산 할 수 있다.

C^= M^Φ^C m o d a l Φ^T M^

(18)

축소모델링 과정을 거친 운동방정식 식 (13)과 업데이트된 감쇠계수 행렬을 포함한 전체 운동방정식은 다음과 같이 표현된다.

M^u^¨ + C^u^˙ + K^u^= f^

(19)

3. 하중 및 응답 추정

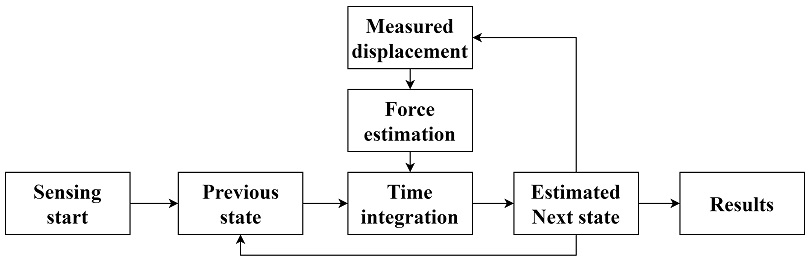
이 연구의 목적인 미측정 지점의 실시간 과도응답(transient analysis) 추정을 위해서는 시간에 따른 구조물의 응답을 빠르게 추정할 수 있는 알고리즘의 도입이 요구된다. 이를 위해 업데이트 과정을 통해 신뢰성이 향상된 유한요소 모델과 시간적분 알고리즘을 활용하여 구조물의 응답을 추정할 수 있도록 구성하였다. Fig. 3에 실시간 연산부의 구성을 도시하였다. 이 연구에서는 대표적인 Implicit 시간적분 기법의 하나인 Newmark-β 시간적분 기법⁽¹³⁾을 적용하였다. 일반적인 Newmark-β 시간적분 과정은 Table 1에 정리 된 바와 같다.

Fig. 3

Real-time estimation process

Table 1

Newmark-β time integration procedure

이 연구에서는 측정 센서를 최소화하기 위하여 레이저센서 1개소에서 측정된 변위 데이터만을 입력으로 활용한다. Newmark-β 기법은 작용하중을 입력으로 하여 변위, 속도, 가속도를 연산하도록 구성되어 있다. 따라서, 측정된 변위 데이터를 활용하여 작용하중을 예측해 수치 적분시 작용하중 항으로 활용하였다. 이를 통해 제한된 측정 데이터를 기반으로 구조물 전체의 변위, 속도, 가속도, 작용 하중을 실시간으로 추정하였다. 이 연구에서는 변위 데이터만을 고려하여 알고리즘을 제안하였으나, 속도 및 가속도 또는 하중을 측정하였을 경우에도 유사한 방식의 가상 센서 시스템 구성이 가능하다.

작용 하중 추정치의 연산을 위해 Newmark-β 적분 기법의 일부 식을 차용하여 활용하였다. 가장 먼저 현재 구조물 변위 ^tu 에서 외력이 작용하지 않았다고 가정하였을 때 관성력에 의해 변화된 다음 상태를 ^{t +Δt}u^I 라고 정의하였으며, 외력이 작용해 변형된 실제 작용 하중 추정치의 연산을 위해 Newmark-β 적분 기법의 일부 식을 차용하여 활용하였다. 가장 먼저 현재 구조물 변위 ^tu 에서 외력이 작용하지 않았다고 가정하였을 때 관성력에 의해 변화된 다음 상태를 ^{t +Δt}u^I 라고 정의하였으며, 외력이 작용해 변형된 실제 구조물에서 측정된 변위를^{t +Δt}u^F 라고 정의하였다. 상첨자 ^I , ^F 는 각각 관성력 및 외력을 의미한다.

실제 구조물에서 변위를 측정하는 동시에, 유한요소 모델에 관성력 만을 적용하여 동일 시점의 변위를 계산하였다. 이때 실제 구조물과 유한요소 모델의 변위의 차는 구조물에 가해진 외력에 의해 발생했다고 가정할 수 있다. 이때 관성력과 실제 구조물에 가해진 유효하중은 Table 1의 Step 2.1을 참고하여 식 (20)과 같이 표현할 수 있다.

r ~ i = t + ∆ t r t + ∆ t + F i, i ∈ I, F

(20a)

r t + ∆ t = 0 w h e n i ∈ I

(20b)

F = M a 0 t u + a 2 t u ˙ + a 3 t u ¨ + C a 1 t u + a 4 t u ˙ + a 5 t u ¨

(20c)

시간적분 알고리듬 연산 과정에 따라, Step 2.2에서 각 시스템의 다음 순간 변위는 식 (21)과 같이 계산된다.

u i t + ∆ t = K ~ - 1 r ~ i t + ∆ t, i ∈ I, F

(21)

이때 외력에 대한 변위와 관성에 의한 변위 차를 수식으로 나타내면 식 (22)와 같다.

∆ u = t + ∆ t K ~ - 1 ∆ r ~ t + ∆ t

(22a)

∆ u = t + ∆ t u F t + ∆ t - u I t + ∆ t

(22b)

∆ r ~ = t + ∆ t r ~ F t + ∆ t - r ~ I t + ∆ t

(22c)

여기에서, 외력에 의한 변위(^{t +Δt}u^F ) 는 실제 센서를 통해 측정되며, 관성에 의한 변위(^{t +Δt}u^I ) 및 하중( $r ~ I t + ∆ t$ )은 유한요소 모델을 통해 계산할 수 있다. 따라서 식 (22)에서의 변수는 외력( $r ~ F t + ∆ t$ ) 하나만 남게 된다. 만약 유한요소 모델이 충분히 보정되어 실제 구조물의 특성을 높은 정밀도로 표현하고 있다고 가정하면 유효하중의 관성과 감쇄항을 식 (23)과 같이 기술할 수 있다.

F I ≈ F F

(23)

식 (23)을 식 (22)에 대입하여 동일항을 소거하면, 식 (24)와 같이 정리할 수 있다.

∆ u t + ∆ t ≈ K ~ - 1 r t + ∆ t

(24)

식 (24)를 이용하면 구조물에 실제로 작용하는 외력^{t +Δt} r을 계산할 수 있다.

그러나, 실제 구조물 변위 정보는 일부 지점에서만 측정되었으므로, 식 (24)의 직접 연산은 불가능하다. 하중 작용 지점과 동일한 지점에 측정된 변위의 차를 ^{t +Δt} Δu^m 라고 하고, 식 (24)를 측정 지점과 미측정 지점으로 분할하면 식 (25)와 같이 다시 표기할 수 있다.

K ~ m K ~ c K ~ c T K ~ u ∆ u m t + ∆ t ∆ u u t + ∆ t ≅ r m t + ∆ t r u t + ∆ t

(25)

예제 구조물과 같이 측정 지점과 하중 작용 지점이 동일하다면, 미측정 지점에서의 작용 하중은 0이라고 가정할 수 있다.

K ~ m K ~ c K ~ c T K ~ u ∆ u m t + ∆ t ∆ u u t + ∆ t ≅ r m t + ∆ t 0

(26)

식 (26)의 행렬식을 이용해 미측정 지점을 측정 지점의 정보로 표현하면 식 (27)과 같이 정리된다.

K ~ m - K ~ c K ~ u - 1 K ~ c T ∆ u m t + ∆ t ≅ r m t + ∆ t

(27)

이를 활용하면 최종적으로 측정지점의 변위 정보를 활용하여 작용 하중의 추정이 가능하다. 이를 이용해 Step 2.1의 유효하중을 계산 후 Table 1의 절차를 반복하여 미계측 지점의 응답(변위, 속도, 가속도)를 계산할 수 있다.

4. 시스템 구성

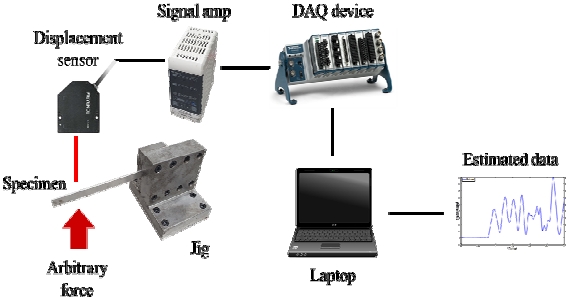
이 단원에서는 앞서 정리한 유한요소 모델 업데이트 과정과 실시간 가상센싱 알고리즘을 포함한 전체 가상 센서 시스템의 구성을 설명한다. Fig. 4는 제작된 가상 센서 시스템의 하드웨어 구성을 나타낸다. 레이저 센서를 활용하여 1개 지점에서의 변위 응답을 직접 측정하였다. 측정된 변위 신호는 신호 앰프(signal amp) 및 데이터 수집 장비(data acquisition device) 등 신호처리 장치를 거쳐 연산장치로 입력되었다. 입력된 변위 신호는 연산장치 내의 실시간 응답추정 알고리듬에 의해 미측정지점 응답 추정에 활용되며, 추정된 응답은 연산장치 내에 저장된다. Fig. 5는 가상 센서 시스템의 실제 구현 및 설치된 장비 구성이다.

Fig. 4

Hardware schematic diagram of virtual sensing

Fig. 5

Test device setup

이 연구에서는 외팔보 형태의 사각형 판(plate) 형태의 구조물 표면에 임의의 하중이 부여된 상황을 가정하였으며, Fig. 4에 표기된 위치에 임의의 하중을 부여하였다. 하중 부여지점과 동일한 지점에 레이저 변위계를 장치하여 하중에 의한 응답 변위를 측정하였다. 구조물은 알루미늄 6061 재종을 사용하여 제작 되었으며, 폭 170 mm, 너비 12 mm, 두께 2 mm의 치수로 제작되었다. 구조물의 끝단 30 mm는 고정구에 삽입되어 고정되었다.

이의 유한요소 모델은 Mindlin–Reissner 평판 요소로 구성되었다. 총 3377개 요소, 5523개 자유도를 사용하였다. 이때 일부 자유도는 구속조건 적용에 의해 제외되었으며, 이에 따라 전체 5487개 자유도가 실제 모델링에 활용되었다. 유한요소 모델의 탄성계수는 69 Gpa, 밀도는 2800 kg/m³, 푸아송비는 0.3으로 가정하였다. 이때 밀도 및 형상은 직접 측정을 통해 사전 업데이트 되었다.

5. 모델 업데이팅 결과

초기 구성된 유한요소 모델의 탄성계수 및 감쇠계수는 2장에서 제시된 업데이트 과정을 통해 갱신되었다. 이 절에서는 실제 구조물 업데이트 과정에서의 계수변화 및 업데이트에 의한 신뢰성 향상 효과를 서술한다.

5.1 고유진동수 업데이트

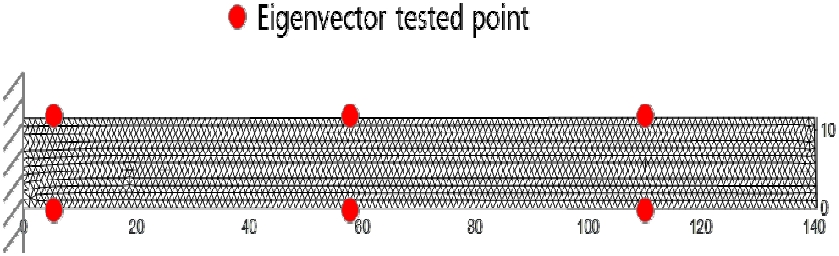
유한요소 모델의 업데이트를 위해 하위 3개 모드의 고유진동수와 고유벡터를 측정하여 사용하였다. 고유진동수 및 고유벡터는 Fig. 6에서 붉은색 점으로 표시된 총 6개 지점에서 충격해머 실험과 레이저 센서로 측정되었다.

Fig. 6

Eigenvector test point

이를 기반으로 유한요소 모델의 민감도 기반 업데이트를 적용하였으며, 탄성계수를 변수로 활용하였다. 그 결과 탄성계수는 업데이트 전 69 Gpa에서 업데이트 후 71.06 Gpa로 소폭 증가하였다. Table 2는 업데이트 전과 후, 그리고 실험에서 계측된 고유진동수를 정리한 것이며, Table 3은 이의 상대오차를 나타낸다. 이를 통해 유한요소 모델의 고유진동수는 업데이트 후 1~3차 모드 전체에서 실험값과 근사하게 개선이 이루어졌음을 확인할 수 있다. 고유벡터의 경우 보정 전 유한요소 모델과 실제 모델의 MAC 수치가 0.9이상의 높은 정확도를 보여 이 연구에서는 추가적인 보정을 진행하지 않았다.

Table 2

Eigenvalue change after update

Table 3

Eigenvalue relative error change after update

5.2 모델 차수 축소

업데이트 된 유한요소 모델의 축소모델링을 위해 저차의 30개 모드, 경계영역에 해당하는 21개 자유도를 활용하였다. 그 결과 차수 축소 전 5487개 자유도에서 축소 후 51개 자유도로 1 % 미만의 자유도를 갖는 축소모델을 개발하였다. Table 4는 원본 모델과 축소 모델의 자유도 구성을 나타낸다. 경계영역 자유도로 사용된 지점은 Fig. 7에 붉은색 점으로 표기된 지점과 같다.

Table 4

DOF change after order reduction

Fig. 7

Reduced-order modeling

5.3 감쇠계수 업데이트

모델 업데이트의 마지막 절차로 감쇠계수에 대한 검증 및 업데이트를 진행하였다. 모든 차수의 감쇠계수를 1 %로 일정하게 부여한 원본 시스템과, 실험에서 얻어진 감쇠계수를 활용해 업데이트된 모델 간의 차이를 비교하였다. Table 5는 업데이트 과정에 사용된 모드별 감쇠계수를 나타낸다.

Table 5

Eigenvalue change after update

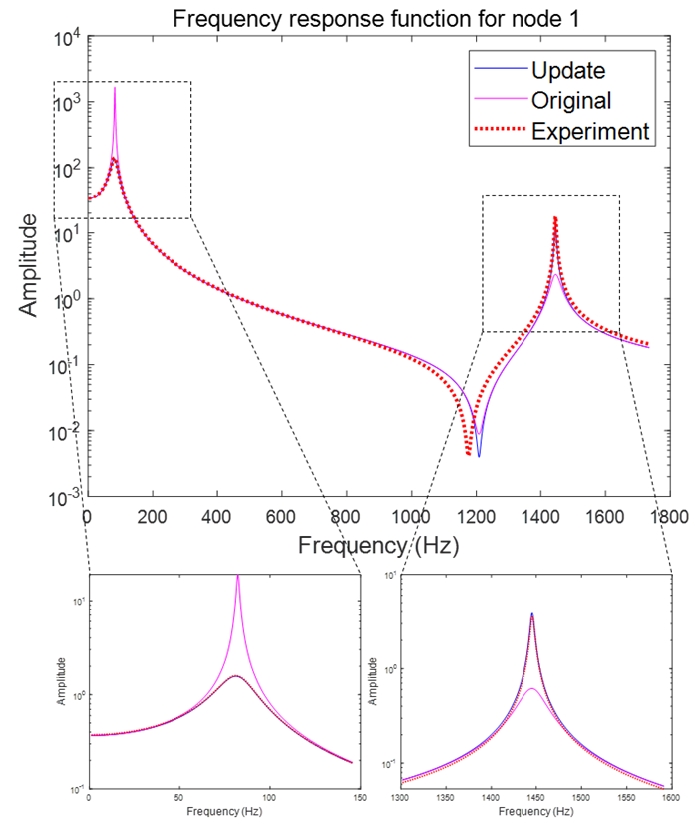
주파수 응답 함수를 기준으로 한 레이저센서 측정 지점에서의 FRAC 값은 업데이트 전 1차 ~ 3차에서 각각 0.53, 0.83, 0.69에서 업데이트 후 모두 0.99 이상으로 높은 주파수 응답 유사성을 띠도록 향상되었다. Table 6은 업데이트 전/후의 각 모드 FRAC 값을 나타낸다.

Table 6

FRAC value change after update

Fig. 8은 동일 지점에서의 주파수 응답 곡선을 비교한 것이다. 업데이트가 완료된 시스템의 곡선은 실험 데이터로 구성된 곡선과 높은 유사성을 보였으며, 업데이트 전 초기 모델에 비해 높은 유사성을 띄는 것으로 확인되었다.

Fig. 8

Comparison of frequency response functions

6. 가상 센싱 성능 검토

이 장에서는 개발된 가상 센서 시스템의 성능을 검증하기 위해 임의의 지점에서 예측된 변위 및 하중의 정확도를 추가적으로 계측된 값과 비교 검증하였다.

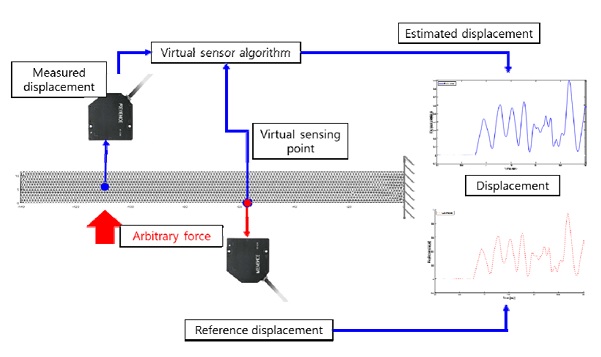
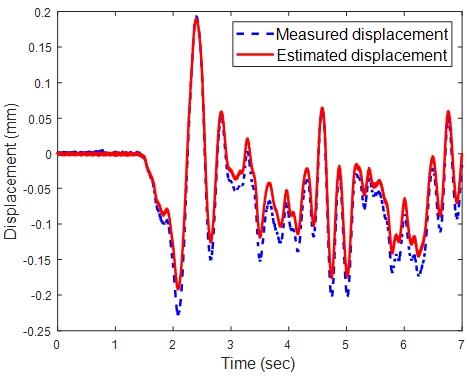
먼저 변위 예측 정확도 검증을 위해 Fig. 9와 같이 구조물 자유단 부근 파란색 점으로 표시된 지점의 변위를 레이저 센서를 이용하여 측정하였으며, 동일한 지점에 임의의 하중을 부여하였다. 개발된 가상 센서시스템을 이용해 구조물 중앙부의 빨간색 점으로 표시된 지점의 변위응답을 추정하였으며, 이를 검증하기 위해 동일지점에서 변위를 레이저센서로 추가 측정하였다. Fig. 10은 이의 비교를 정리한 것으로, 실제 계측치와 가상 센서 추정치가 높은 정확도를 갖는 것을 확인할 수 있다.

Fig. 9

Displacement validation test description

Fig. 10

Comparison of estimated displacement

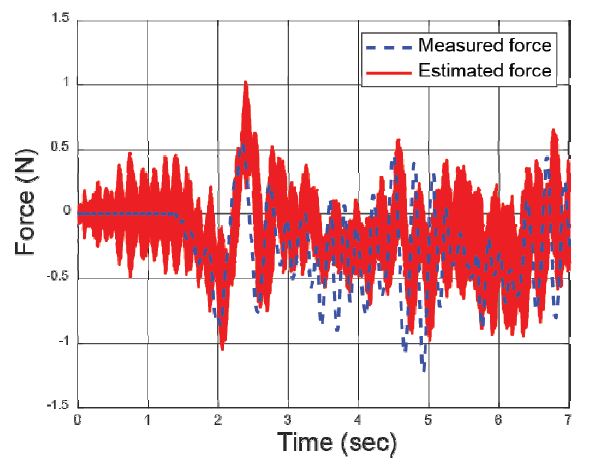
추가적으로 가상 센서의 하중 예측 정확도를 검증하기 위하여, Fig. 11과 같이 임의의 변위를 가력한 위치의 실제하중을 로드셀을 통해 측정하여 비교하였다. 해당 지점의 변위정보만을 활용하여 가상 센서 시스템 내에서 추정된 하중은 Fig. 12와 같이 실제 로드셸을 통해 계측된 하중과 근사한 것으로 확인할 수 있다. 다만, 앞서 Fig. 10의 변위 추정값에 비해 정확도 면에서 불규칙한 진동 성분이 확인되었으며, 추후 연구를 통해 노이즈를 개선작업이 수행될 필요가 있다. 개발된 가상센서 시스템은 PC의 MATLAB 환경에서 개발 및 테스트되었으며, 사양 및 버젼은 Table 7과 같다.

Fig. 11

Force validation test description

Fig. 12

Comparison of estimated applied force

Table 7

Specifications of PC & Software

구성된 가상센서 시스템을 활용하여 실제 구조물에서 10초(10 000개 데이터) 간 측정된 실험 데이터를 처리하는데 약 0.4573초가 소모되었다. Table 8은 전체 측정 시간, 얻어진 실험 데이터를 처리하는데 소모된 연산시간, 1개 시간스텝 연산에 소모된 평균 연산시간을 정리한 것으로 고속연산을 통한 실시간 센싱이 가능함을 보여준다. 그러나 개발된 기술의 실구조물 적용 시 실제 연산 성능은 계측장비, 적용대상구조물, 경계조건 등에 따라 상이할 수 있어, 관련한 연구개발이 요구된다.

Table 8

Elapsed time result of virtual sensing

아울러 이 연구에서는 가상 센서 시스템의 성능을 변위와 하중에 대해서만 검토하였으나, 향후 다양한 후처리(post-processing) 연산기의 개발을 통해 연구자의 필요에 따른 시스템 개발이 가능할 것으로 판단된다. Fig. 13은 이상적인 가상 센서 시스템의 예를 보여주는 것으로 개발된 기술을 확장하여 모델 전체의 변위, 변형량, 응력 등의 실시간 연산 및 AR/VR기반 시각화에 활용할 수 있을 것으로 판단된다.

Fig. 13

An example of virtual sensor system

7. 결 론

이 연구에서는 최소한의 계측 정보를 기반으로 미계측 지점 또는 미계측 진동 정보의 실시간 추정을 위한 가상 센서 시스템을 제안하였다. 이를 위해 일차적으로 유한요소법 및 이의 업데이팅 기법을 통해 실제 구조물과 동일한 구조진동 특성을 갖는 물리모델을 생성하였으며, 계산속도 향상 및 실모델-유한요소모델의 동기화를 위해 전통적인 축소 모델링 기법을 보정하여 활용하였다. 추가적으로 적분기 및 응답추정 알고리즘 역시 제안된 가상 센서 시스템에 맞게 수정하였다. 개발된 시스템의 성능은 외팔보 시편을 대상으로 실제로 구축하여 검증하였다.

향후 이 연구에서 제안한 가상 센서 시스템의 실제적인 적용을 위해 복잡한 구조진동 구조물에 대해 성능검증을 진행하고자 한다. 이 경우 최신의 축소모델링 기법⁽¹⁶⁾, 시간적분 알고리즘의 탐색 및 적용 등을 통한 시스템의 정밀도와 계산효율 향상이 요구될 수 있다. 아울러 제안된 시스템은 발전설비 배관 및 각종 기계설비의 실시간 상태 감시/건전성관리 등을 위해 다양한 디지털 트윈 시스템으로 확장될 수 있을 것으로 기대된다. 이를 위해서는 유체-구조 상호 작용(Fluid-Structure Interaction, FSI)^(17,18), 유연 다물체 동역학(Flexible Multibody Dynamics, FMBD)^(19,20) 등의 고성능 수치모델링 및 축소모델링 기법이 요구된다.

기 호 설 명


M :	질량 행렬
C :	감쇠 행렬
K :	강성 행렬
u :	변위 벡터
q :	모달좌표계 벡터
f :	힘 벡터
φ :	고유벡터
λ :	고유진동수
I :	단위 행렬
T :	변환행렬
ω :	가진주파수
ξ :	감쇠계수
α :	주파수 응답 함수
r :	시간적분 유효 하중
c :	축소모델 커플링 자유도
d :	축소모델 주요 모드
l :	모달실험 하중 작용점
k :	모달실험 실험 측정지점

Acknowledgments

This research was supported by the Basic Science Research Programs through the National Research Foundation of Korea funded by the Ministry of Science, ICT, and Future Planning (NRF-2018R1A1A1A05078730)

References

Choi, J. H., Yun, Y. and Kim, S., 2017, A Study for Aircraft Actuator Health Management based on Extended Kalman Filters, Proceedings of the KSNVE Annual Autumn Conference, p. 215.
Lee, S. H. and Yun, B. D., 2015, Directions of Industry 4.0 and Prognostics and Health Management (PHM), Journal of KSNVE, Vol. 25, No. 1, pp. 22~28.
Cho, S. H., 2019, FE Model Updating of Tall Buildings Using Output-only Modal Data, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 131~140. [https://doi.org/10.5050/KSNVE.2019.29.1.131]
Risaliti, E., Tamarozzi, T., Vermaut, M., Cornelis, B. and Desmet, W., 2019, Multibody Model Based Estimation of Multiple Loads and Strain Field on A Vehicle Suspension System, Mechanical Systems and Signal Processing, Vol. 123, pp. 1~25. [https://doi.org/10.1016/j.ymssp.2018.12.024]
Friswell, M. I. and Mottershead, J. E., 1995, Finite Element Model Updating in Structural Dynamics, Springer Science & Business Media, Netherlands, pp. 7~35. [https://doi.org/10.1007/978-94-015-8508-8_2]
Fox. R. L. and Kapoor. M. P., 1968, Rates of Changes of Eigenvalues and Eigenvectors, AIAA Journal, Vol. 6, No. 12, pp. 2426~2429. [https://doi.org/10.2514/3.5008]
Alvin, K. F., 1997, Efficient Computation of Eigenvector Sensitivities for Structural Dynamics, AIAA Journal, Vol. 35, No. 11, pp. 1760~1766. [https://doi.org/10.2514/2.24]
Lim, J. H., Hwang, D. S., Sohn, D.W. and Kim, J. G., 2016, Improving the Reliability of the Frequency Response Function Through Semi-direct Finite Element Model Updating, Aerospace Science and Technology, Vol. 54, pp. 59~71. [https://doi.org/10.1016/j.ast.2016.04.003]
Allemang, R. J. and Brown, D. L., 1982, A Correlation Coefficient for Modal Vector Analysis, Proceedings of the 1st International Modal Analysis Conference, pp. 110~116,.
Craig, R. R. and Bampton, M. C. C., 1968, Coupling of Substructures for Dynamic Analyses, AIAA journal, Vol. 6, No. 7, pp. 1313~1319. [https://doi.org/10.2514/3.4741]
Pascual, R., Golinval, J. C. and Razeto, M., 1997, A Frequency Domain Correlation Technique for Model Correlation and Updating, Proceedings of the International Modal Analysis Conference IMAC, pp. 587~592.
Maia, N. M. M. and Silva, J. M. M., 1998, Theoretical and Experimental Modal Analysis, Research Studies Press, Hertfordshire.
Bathe, K. J., 2006, Finite Element Procedures, 2nd Edition, Prentice Hall, Pearson Education, USA.
Kim, J. G., Park, Y. J., Lee, G. H. and Kim, D. N., 2017, A General Model Reduction with Primal Assembly in Structural Dynamics, Computer Methods in Applied Mechanics and Engineering, Vol. 324, pp. 1~28. [https://doi.org/10.1016/j.cma.2017.06.007]
Guyan, R. J., 1965, Reduction of Stiffness and Mass Matrices. AIAA Journal, Vol. 3, No. 2, p. 380. [https://doi.org/10.2514/3.2874]
Kim, J. G. and Lee, P. S, 2015, An Enhanced Craig–bampton Method, International Journal for Numerical Methods in Engineering, Vol. 103, No. 2, pp. 79~93. [https://doi.org/10.1002/nme.4880]
Kim, S. M., Kim, J. G., Chae, S. W. and Park, K. C., 2019, A Strongly Coupled Model Reduction of Vibro-acoustic Interaction, Computer Methods in Applied Mechanics and Engineering, Vol. 347, pp. 495~516. [https://doi.org/10.1016/j.cma.2018.12.029]
Kim, S. M., Chae, S-W., Park, K. C. and Kim, J. G., 2019, Performance of Multiphysics Model Reduction of Vibro-acoustic Coupled Problem, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 500~510. [https://doi.org/10.5050/KSNVE.2019.29.4.500]
Kim, J. G., Han, J. B., Lee, H. and Kim, S. S, 2018, Flexible Multibody Dynamics Using Coordinate Reduction Improved by Dynamic Correction, Multibody System Dynamics, Vol. 42, No. 4, pp. 411~429. [https://doi.org/10.1007/s11044-017-9607-2]
Han, J. B., Kim, J. G. and Kim, S. S., 2019, An Efficient Formulation for Flexible Multibody Dynamics Using a Condensation of Deformation Coordinates, Multibody System Dynamics, Vol. 47, No. 3, pp. 293~316. [https://doi.org/10.1007/s11044-019-09690-4]

Seungin Oh received his B.S. degree in Department of Mechanical Engineering from Kyung Hee University in 2019. He is currently a M.S. candidate in mechanical engineering department at Kyung Hee University. His research interests include finite element model updating, virtual sensing and cyber physical system.

Jai-Kyung Lee received his B.S. and M.E. degrees in Computer Engineering from Ajou University in 1995 and 1997, respectively, and his Ph.D. in Computer Engineering from Chungnam National University in 2008. He is currently a Principal Researcher of Korea Institute of Machinery and Materials. His research interests include intelligent systems, monitoring and big data analytics of smart machines.

Jin-Gyun Kim received his B.S. and M.E. degrees in Civil Engineering from Korea University in 2008 and 2010, respectively, and his Ph.D. in ocean systems engineering from Korea Advanced Institute of Science and Technology (KAIST) in 2014. He worked as a senior researcher in Korea Institute of Machinery and Materials (KIMM) from 2014 to 2017. He is currently an Assistant Professor of Kyung Hee University of Mechanical Engineering.

	Original	Update	Experiment
Mode1 (Hz)	81.023	82.221	82.280
Mode2 (Hz)	509.001	516.525	516.060
Mode3 (Hz)	1424.373	1445.427	1445.685

	Original	Update
Mode1	1.551	0.072
Mode2	1.387	0.090
Mode3	1.496	0.018

CPU	RAM	OS version	MATLAB version
3.7Ghz 6 Cores 12 Threads (Intel i7-8700K)	32 GB	Windows 10	R2019b

Step 1. Initial calculation
Step 1.1 Setup initial value $u 0, u ˙ 0, u ¨ 0$ Step 1.2 Calculate coefficients. $a 0 = 1 α Δ t 2, a 1 = δ α Δ t, a 2 = 1 α Δ t, a 3 = 1 2 a - 1, a 4 = δ α - 1, a 5 = Δ t 2 δ α - 2, a 6 = Δ t 1 - δ, a 7 = δ Δ t$ Step 1.3 Calculate effective stiffness $K ~ = K + a 0 M + a 1 C$
Step 2. Iterative calculation
Step 2.1 Calculate effective load differences $r ~ = t + Δ t r + M a 0 u t + a 2 u ˙ t + a 3 u ¨ t t + Δ t + C a 1 u t + a 4 u ˙ t + a 5 u ¨ t$ Step 2.2 Calculate displacement for next step $u t + Δ t = K ~ - 1 r ~ t + Δ t$ Step 2.3 Calculate accelerations and velocities for next step $u ¨ t + Δ t = a 0 u t + Δ t - u t - a 2 u ˙ t - a 3 u ¨ t u ˙ t + Δ t = u ˙ t - a 6 u ¨ t - a 7 u ¨ t + Δ t$