유한요소해석을 이용한 중량충격원 종류 및 평가지표 별 바닥충격음 예측 정확도 검증

1. 서 론

공동주택은 세대 간 경계벽, 바닥구조 등 많은 부분을 이웃 세대와 공유하고 있기 때문에 소음 피해에 취약한 구조적 특성을 갖고 있다. 특히 상부 세대 충격에 의해 발생하는 바닥충격음은 층간소음 민원 중 가장 많은 비중을 차지하고 있으며, 최우선적으로 해결해야 할 사회적 과제이다⁽¹⁾.

바닥충격음 저감을 위해 제도 개선⁽²⁾, 기술 개발 등 많은 연구가 진행 중에 있으나⁽³⁾, 다양한 설계·시공변수 별 바닥충격음 저감 효과를 실험을 통해 검증하기에는 시간적, 경제적 측면에서 많은 한계점이 존재한다. 따라서 컴퓨터 시뮬레이션을 이용한 바닥충격음 예측 연구가 대두되고 있으며, 충격원 종류에 따른 다양한 해석 기법이 적용 중이다^(4,5). 일반적으로 바닥충격음을 예측하기 위해 유한요소법(finite element method, FEM), 통계적 에너지 해석법(statistical energy analysis, SEA), 경계요소법(boundary element method, BEM)이 이용되고 있으며, 중량충격음의 경우 유한요소법이, 경량충격음의 경우 통계적 에너지 해석법이 유용한 것으로 알려져 있다^(6,7).

바닥충격음 예측 시 해석 모델을 외란(noise)가 없는 선형 시스템(linear system)으로 가정하면 바닥충격음 발생 메커니즘을 입력신호(충격원), 주파수응답함수(해석모델), 출력신호(바닥충격음)로 정의할 수 있다. 주파수응답함수(frequency response function)란 입력신호에 대한 출력신호의 비로 정의되며, 주파수응답함수를 이용하는 경우 입력 변화에 따른 출력을 손쉽게 예측할 수 있는 장점이 존재한다. 선행연구에서는 실험적으로 바닥충격음 발생 과정의 주파수 응답함수를 정의하여 충격원에 따른 바닥충격음을 예측하였으며, 신뢰성 있는 바닥충격음 예측 결과를 도출하였다⁽⁸⁾.

현재, 중량충격음에 대한 KS 평가방법은 뱅머신 또는 고무공 충격원을 이용하여 바닥충격음 레벨(L_i,Fmax)을 측정 후, 바닥충격음 차단성능 단일수치(L_i,Fmax,AW)로 평가하게 된다. 현재 국내 고시 상에서는 뱅머신을 이용한 결과에 대하여 등급화를 반영하고 있으나, 과도한 충격력 특성으로 인해 실제 거주자 행위 충격력에 의한 바닥충격음 차단성능과의 차이가 발생한다는 문제점이 지속적으로 제기되고 있다. 이에 대한 대안으로, ISO에서는 고무공을 표준충격원으로 채택하여 중량충격음에 대한 차단성능 실험을 수행하고 있으나, 각 충격원 별 충격력 및 스펙트럼 차이로 인해 동일 바닥구조에 대한 차단성능 실험결과에서도 차이가 발생하는 것으로 보고되고 있다. 또한, 평가지표 변화에 따라 주관적 반응 차이를 보이고 있어, 설계단계에서 충격원 별 다양한 중량충격음 평가지표에 대한 예측을 통한 구조체 차음 대책수립이 필수적이다.

이에, 이 연구에서는 바닥충격음 발생 메커니즘을 선형시스템의 주파수응답함수로 정의하여 유한요소 해석법을 활용한 바닥충격음 해석 결과의 신뢰성을 검증하였다. 벽식구조의 실증주택을 대상으로 연구를 진행하였으며, 바닥충격음 신뢰성 분석에 앞서 개별적인 구조모델과 음향모델을 구성하여 진동, 음향 특성의 예측 정확도를 실험결과와 비교 분석하였다. 바닥충격음은 중량충격원인 뱅머신과 임팩트볼에 대해 측정 시험과 병행하여 예측을 수행하였으며, 중량충격음 평가지표에 따른 바닥충격음 예측 신뢰성을 검증하였다.

2. 배경 이론

2.1 에너지평형식을 이용한 바닥충격음 예측

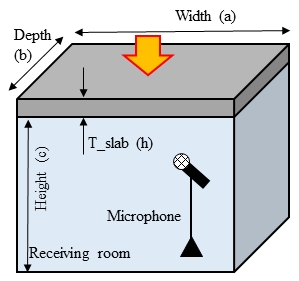
Fig. 1과 같이 바닥 슬래브와 음향 공간으로 구성된 시스템에서 바닥 슬래브를 충격 가진시키면 하부 공간으로 소음이 발생하며, 여기서 에너지는 가진원(충격원) 에너지, 진동 에너지, 음향 에너지 순으로 변환된다. 에너지 변환 시 에너지 손실이 없다고 가정하면 에너지평형식(energy balance equation)을 적용하여 식 (1)과 같이 바닥충격음을 예측할 수 있다⁽⁹⁾.

$\[ L_n\left(\omega \right)=10\log \left(\frac{1.73{\left({\rho }_0{c}_0\right)}^2{\sigma }_{\mathrm{r}\mathrm{a}\mathrm{d}}}{p_{ref}^2{\rho }^2{c}_l\omega \eta A}{\tilde{F}}^2\right) \]$

(1)

Fig. 1

Schematic diagram showing dimensional properties affecting floor impact sound

여기서, ρ₀는 공기의 밀도 (kg/m³), c₀는 공기의 음속(m/s), σ_rad는 바닥 슬래브의 방사효율, ω는 진동수(ω=2πf)(rad/s), c_l은 바닥 슬래브의 종파 속도 (m/s), η는 바닥 슬래브의 손실계수, A는 바닥 슬래브의 너비(m²), F는 가진력(N)을 나타낸다.

일반적으로 바닥 슬래브로 전달되는 에너지를 저감시키기 위해 완충재를 이용한 절연기 형태의 방진 시스템을 적용하고 있으며^(10,11), 표준바닥구조⁽²⁾와 같이 완충재와 상부층(경량기포 콘크리트, 모르타르)를 적층하는 경우 소음 저감 효과는 식 (2)와 같이 정의 할 수 있다.

$\[ ∆L_n\left(\omega \right)=10\log \left[2.3c_{l,s}{\eta }_s{h}_s{n}^{\text{'}}\left({\omega }^3∕{\omega }_s^4\right)\right] \]$

(2)

여기서, n′은 단위 면적 당 마운트의 개수, ω_s은 완충재의 고유 진동수(rad/s), c_l,s은 상부층의 종파속도(m/s), h_s은 완충재 상부층의 두께(m)를 의미한다. 결과적으로 완충재 적용에 따른 바닥충격음 저감 효과는 식(3)을 통해 이론적으로 계산할 수 있다.

$\[ \mathrm{F}\mathrm{l}\mathrm{o}\mathrm{o}\mathrm{r}\mathrm{ }\mathrm{I}\mathrm{m}\mathrm{p}\mathrm{a}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{N}\mathrm{o}\mathrm{i}\mathrm{s}\mathrm{e}=L-∆L \]$

(3)

2.2 유한한 시스템의 모드

유한(finite)한 크기의 시스템에서 동일한 크기의 진폭과 파장의 입사파와 반사파가 구조적 결합되는 경우 정재파(standing wave)가 생성되며 이를 모드(mode)라 한다. 여기서 정재파의 모양은 모드 형상(mode shape)이라 한다⁽¹²⁾.

일반적으로 구조물의 경우 진동 모드가 발생하는 주파수를 고유진동수(natural frequency)라 하며 균일한 재료로 구성된 유한한 직사각형 구조의 경우 이론적으로 식 (4)를 이용하여 진동 모드를 계산 할 수 있다⁽¹³⁾.

$\[ {\omega }^2=\frac{{\pi }^{4}D}{a^4\rho }\left\{G_x^4+G_y^4{\left(\frac{a}{b}\right)}^4+2{\left(\frac{a}{b}\right)}^2\left[v{H}_x{H}_y+\left(1-v\right)J_x{J}_y\right]\right\} \]$

(4)

$\[ D=\frac{E{h}^3}{12\left(1-v^2\right)} \]$

(5)

여기서 D는 굽힘 강성(bending stiffness)(N/m), a는 장축의 길이(m), b는 단축의 길이(m)를 나타내며, G, H, J는 모드 차수 m에 대한 상수로 끝단이 완전구속(clamped)인 경계조건인 경우 Table 1에 정의된다. 음향 공간의 경우 음향 모드 또는 룸모드라 하며, 강체벽으로 둘러쌓인 닫힌 공간의 경우 식 (6)을 이용하여 음향 모드를 계산할 수 있다. 여기서 k²_lmn은 파수(wave number)를 나타내며, l, m, n은 각 길이방향의 모드차수를 나타낸다⁽¹⁴⁾.

$\[ {\mathrm{f}}_{lmn}=k_{lmn}\frac{c}{2\pi } \]$

(6)

$\[ k_{lmn}^2={\left(\frac{l\pi }{a}\right)}^2+{\left(\frac{m\pi }{b}\right)}^2+{\left(\frac{n\pi }{c}\right)}^2 \]$

(7)

Table 1

Frequency coefficients in Eq. (4)

2.3 주파수응답함수

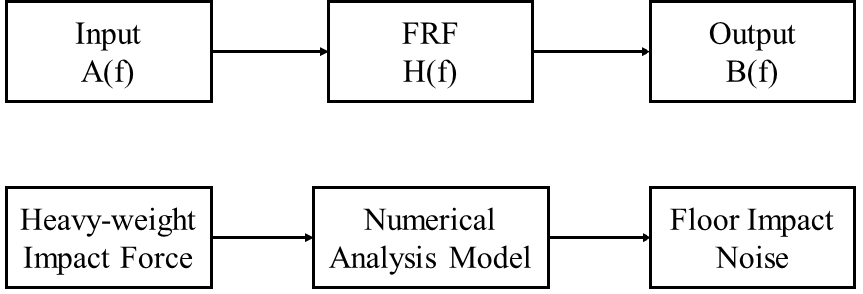
Fig. 2와 같이 외란이 없는 선형시스템의 경우 주파수응답함수(frequency response function) H(f)를 이용하여 입력신호 A(f)에 대한 출력신호 B(f)를 예측 할 수 있다. 일반적으로 주파수응답함수는 시스템의 안정성 등을 평가하는데 이용되며, 적용 목적에 따라 전달함수(transfer function)로도 알려져 있다⁽¹⁵⁾.

Fig. 2

Frequency response function: H(f)

바닥충격음의 경우 충격원을 입력신호, 충격음을 출력신호로 정의하면, 바닥충격음 발생의 모든 메커니즘이 주파수응답함수가 된다. 이러한 주파수응답함수의 특징을 이용하여 충격원에 따른 경량/중량 충격음을 신뢰성 있게 예측할 수 있으며⁽⁸⁾, 주파수응답함수를 세분화 하여 정의한다면 시스템 변화에 따른 효과를 분석할 수 있는 장점이 존재한다. 예를 들어, 바닥충격음 해석 시 해석 시간을 단축하기 위해 바닥적층 구조 모델만을 이용하여 충격원 에너지 저감 효과를 분석 후 맨슬라브 모델에 적용하여도 동일한 바닥충격음 해석이 가능함을 의미한다⁽¹⁶⁾. 따라서 이러한 시스템의 선형성을 이용하여 바닥충격음 해석 모델을 분리 및 결합 적용 할 수 있다.

3. 구조 해석 모델의 신뢰성 검증

3.1 바닥 슬래브의 진동 특성 측정

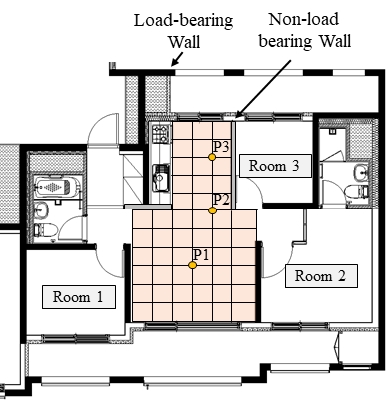
구조 해석 모델의 신뢰성을 검증하기 위해 대표적인 공동주택 평면인 전용면적 59 m²의 실증주택을 대상으로 연구를 수행하였다. 대상세대는 국토부 고시⁽²⁾에 의거하여 거실면적은 13.4 m²이며, 하부층 수음실 부피는 35.5 m³이다. 대상 세대의 바닥 슬래브 두께는 150 mm 로 구성되어 있으며, 완충재를 포함한 뜬바닥 구조가 설치되지 않은 맨슬래브 조건이다. 또한 하부층의 천정구조가 설치되지 않기 때문에 콘크리트 골조 구조만의 진동 특성을 분석 할 수 있도록 실험 조건을 구성하였다. 바닥 슬래브의 모드테스트는 Fig. 3과 같이 거실 공간을 대상으로 수행하였다.

Fig. 3

Experimental set-up to measure vibration characteristic of floor structure

바닥 슬래브의 진동 특성 분석은 임팩트 해머를 이용한 모드 테스트를 수행하였으며, 사용된 측정 장비는 Table 2에 정리하였다. 모드 테스트 측정 시 3개의 가속도계를 고정하고 임팩트 해머의 가진 위치를 이동하며 가속도 응답을 측정하였으며, 주파수 분석기의 분석 주파수는 1024 Hz까지 1 Hz 간격으로 주파수 분석을 할 수 있도록 설정하였다⁽¹⁷⁾.

Table 2

Test equipment for modal test

Fig. 3과 같이 모드 테스트를 수행하기 위해 격자를 구성하였으며, 거실 공간 단축 방향의 3차 모드까지 분석할 수 있도록 격자의 크기를 약 50 cm로, 총 69개의 격자를 구성하였다.

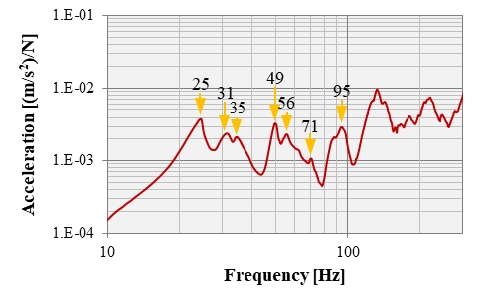
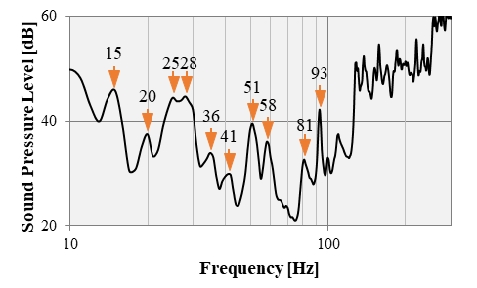
임팩트 해머의 팁은 고무팁을 이용하였으며, 본 실험의 경우 고무팁을 사용하면 재현성(coherence)이 약300 Hz까지 0.9 이상으로 분석되었다⁽¹⁷⁾. 따라서 바닥슬래브의 진동 특성 분석은 300 Hz까지 수행하였으며, Fig. 4는 모드 테스트를 이용하여 측정된 바닥 슬래브의 공간 평균 주파수응답함수를 나타낸다. 주파수 응답함수에서 피크(peak) 주파수와 위상(phase)을 이용하여 고유 진동수를 분석할 수 있으며, 100 Hz 이하 대역에서 분석된 바닥 슬래브 고유진동수를 Fig. 4와 같이 표시하였다. 이 연구 대상의 59 m²의 실증주택의 경우 1차 굽힘 모드는 25 Hz로 분석되었다.

Fig. 4

Frequency response function of floor structure on the living room

3.2 구조 해석모델 구성

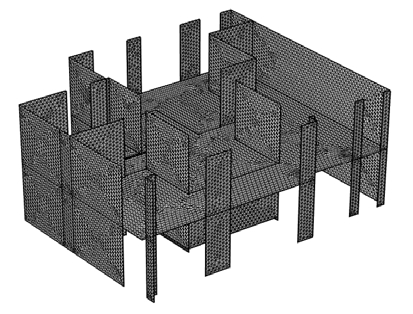
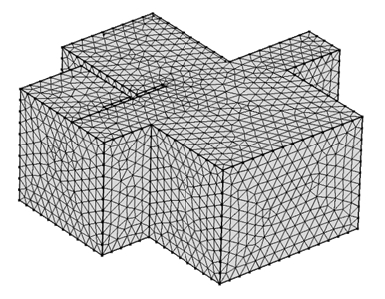
바닥충격음 예측은 음향진동 해석 상용 소프트웨어인 COMSOL Multiphysics 5.3a을 이용하였으며, Fig. 5는 메쉬 상태의 구조 해석모델을 나타낸다. 본 연구에서는 완충재가 설치되어 있지 않은 골조 상태를 대상으로 하기 때문에 효율적인 해석을 위해 슬래브와 벽을 판으로 가정하여 2D element의 triangular elements를 사용하여 모델을 구성하였다. 모드 테스트의 300 Hz 이하 주파수 대역의 측정 결과를 비교 분석 할 수 있기 때문에 구조 모델의 해석 주파수를 300 Hz까지 분석할 수 있도록 설정하였으며, 울타리효과(fence effect)⁽¹⁵⁾에 의한 해석 오차를 방지하기 위해 최대 주파수 파장에 5개의 노드(node)가 구성되도록 하여 총 6041개의 element로 구성하였다.

Fig. 5

Structural analysis model on COMSOL

해석 모델의 경계조건은 벽체 끝단에 고정조건을 입력하였으며, Table 3과 같이 철근 콘크리트 재료의 물성을 입력하였다.

Table 3

Material property of structural model

3.3 구조 해석모델 검증

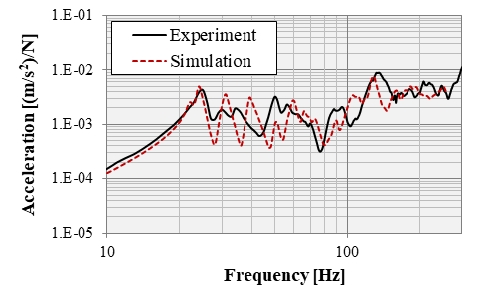
구조 해석 모델에 대한 검증은 Fig. 3의 거실 중앙지점(P1)에 단위 하중 가진 조건에서 구조 해석을 수행하였다. Fig. 6은 가진 지점에서의 가속도 측정 결과와 해석 결과를 나타낸다.

Fig. 6

Comparison of experimental and numerical results: narrow band

측정 결과 대비 해석 결과의 응답의 크기는 유사하나, 피크 주파수에서 일치하지 않는 진동 모드들이 존재하였다. 이는 해석모델 구성 시 속도 의존성이 높은 비선형 재료의 콘크리트 물성을 선형 재료로 가정하였기 때문에⁽¹⁸⁾ 굽힘 강성 변화에 의한 고유 진동수 차이가 발생된 것으로 판단된다. 따라서 콘크리트 재료의 주파수 대역 별 재료 물성을 입력한다면 보다 정확한 해석이 가능할 것으로 판단된다.

콘크리트 재료를 선형시스템으로 가정하는 경우 고유 진동수 차이를 분석하기 위해 추가적으로 고유치 해석을 통해 진동 모드를 분석하였다. 고유 진동수는 구조 해석모델은 고유치 해석(normal mode analysis)을 수행하였으며 바닥 슬래브의 고유 진동수를 분석하였다.

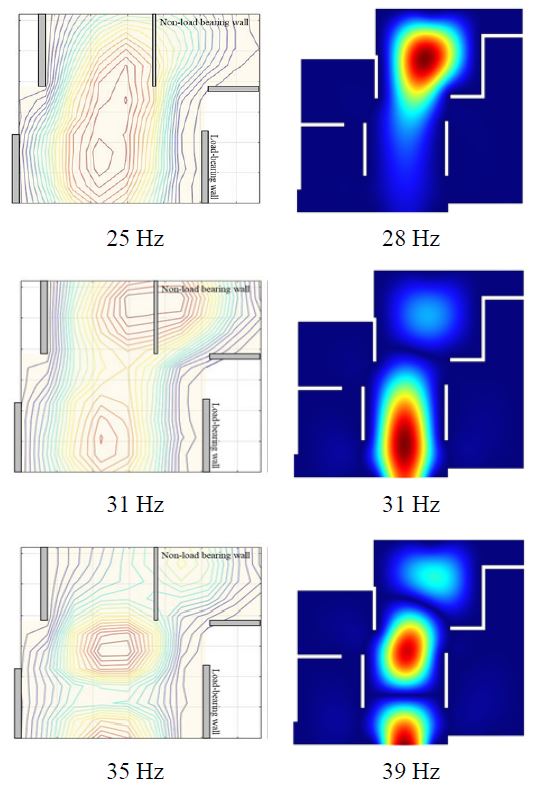
Fig. 7은 3차 모드까지의 모드 테스트와 고유치 해석의 모드 형상을 나타낸다. 그림과 같이 슬래브 진동은 내력벽에 의해 진동 특성이 결정되고 있으며, 비내력벽은 바닥 진동에 대해서는 영향도가 미비한 것을 확인할 수 있다. 유사한 주파수 대역에 진동 주파수가 존재하였으며, 모드 형상 또한 유사하게 분석 되었다. 따라서 전산해석을 이용한 구조 진동 특성 분석 시 실제 구조물의 진동 거동과 유사한 결과를 도출할 수 있을 것으로 판단된다.

Fig. 7

Mode shape of floor structure(left: experimental results, right: numerical results)

4. 음향 해석 모델의 신뢰성 검증

4.1 음향 특성 분석

음향 특성 중 수음실의 구조 형상 및 표면 재료 특성에 의해 결정되는 음향 모드는 바닥충격음 발생 시 수음실의 음장 분포를 결정하며, 이는 수음 위치 별 소음도 차이를 의미한다^(18,19). 바닥충격음 측정 시 공간 내 평균 음압을 측정하기 위해 벽체에서 이격거리 750 mm 지점의 모서리 4지점과 공간 중앙 지점에 마이크로폰을 설치하고 있으며, 최소 750 mm 이격 지점에서 공간 내 평균 소음과 유사한 소음도를 측정할 수 있는 것으로 선행 연구의 결과가 존재한다⁽²⁰⁾.

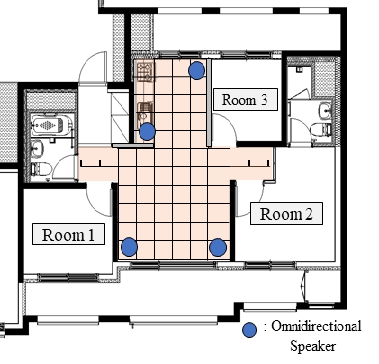
하지만 Fig. 8과 같이 거실 공간이 주방과 통합된 형태의 거실에서 중량충격음을 측정하는 경우 음향모드의 기여도가 높아지기 때문에 수음점 위치 별 소음도 차이가 발생한다. 따라서 경량충격음(1/1 옥타브밴드, 125 Hz ~ 2000 Hz)에 비해 모드 밀도가 낮은 중량충격음(1/1 옥타브 밴드, 63 Hz ~ 500 Hz) 분석 시 음향 특성을 고려 할 필요가 있다. 이에, 수음실의 음향모드를 기준으로 해석모델의 신뢰성을 분석하였으며, 음향모드 측정은 ISO 3741를 이용하여 정상상태의 수음실 내 음장 분포를 측정하였다⁽²¹⁾.

Fig. 8

Experimental set-up to measure acoustic characteristic of receiving room

Fig. 8과 같이 모드 테스트 격자와 동일하게 하부층에도 격자를 구성하였으며, 7개의 마이크로폰(GRAS, 146AE)을 이동하며 평균 소음을 측정하였다. 소음원위치는 특정 모드의 영향을 최소화 하기 위해 그림과 같이 4개의 모서리 위치를 선정하여 실험을 수행하였으며, 무지향스피커(NTEC, OMNI 4)를 이용하여 수음실이 최대한 정상상태 조건을 만족하도록 구성하였다. 음원 위치 별 총 4가지 조건에서 실험을 수행하였으며, Fig. 9는 각 조건에 대한 산술 평균한 소음도 측정 결과를 나타낸다. Fig. 9에서 피크 주파수는 음향모드를 의미하며⁽¹⁸⁾, 100 Hz 이하의 음향 모드를 그림과 같이 표시하였다. 반면 100 Hz 이후 대역에서는 음향모드가 급격하게 증가하는 것을 확인 할 수 있다.

Fig. 9

Experimental result of acoustic characteristic in the living room

4.2 음향모델 구축 및 모델 검증

수음실의 음향모델은 실제 음장을 최대한 구현할 수 있도록 Fig. 10과 같이 벽체를 기준으로 연결된 공간을 모두 모델링 하였으며, 벽체는 마감이 되어 있지 않기 때문에 콘크리트의 음향 임피던스를 입력하여 실제 수음실 음장 조건과 유사하게 구성하였다. 음향 공간은 공기로 설정하였으며, 입력된 물성은 Table 4에 정리하였다.

Fig. 10

Acoustic analysis model on COMSOL

Table 4

Material property of acoustic model

해석모델의 격자는 구조 해석모델과 동일하게 300 Hz까지 분석할 수 있도록 격자의 크기를 구성하여, 총 18041개의 tetrahedral elements를 사용하였다.

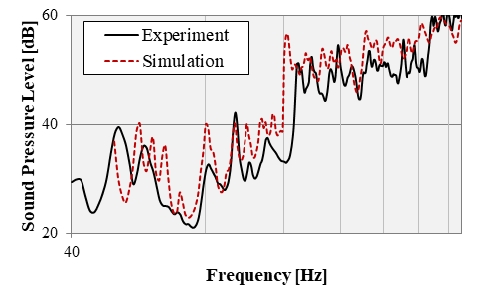
음원은 Fig. 8과 같이 위치시켜 4개의 모델을 구성하였으며, 스피커와 근접한 위치에서 측정된 음압을 스피커 출력으로 가정하여 해석 모델의 점음원으로 구성하였다. 해석 주파수는 중량충격음 평가 대역인 45 Hz부터 1 Hz 간격으로 해석을 수행하였다. Fig. 11은 점음원 발생 시 공간 평균의 소음도 해석 결과를 나타내며, 수음실 측정 결과와 함께 도시화 하였다. 그림과 같이 100 Hz 이하 대역에서 개별적인 모드 비교가 가능하며, 측정 결과 대비 유사한 해석 결과를 확인 할 수 있다. 반면, 100 Hz 이후 주파수 대역에서는 모드 밀도가 높아지는 것을 확인 할 수 있으며, 에너지 측면에서 측정 결과와 유사한 것을 확인 할 수 있다.

Fig. 11

Comparison of experimental and numerical results: narrow band

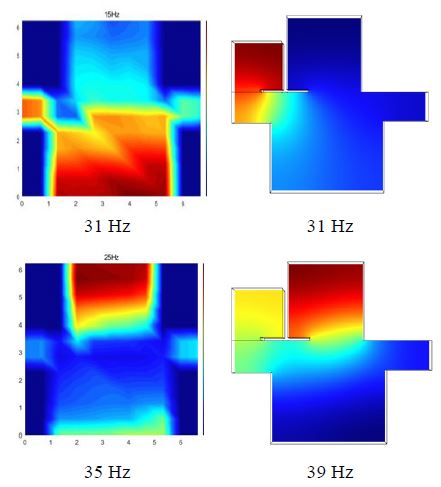
음향 모드를 비교하기 위해 수음실 공간에 대해 고유치 해석을 수행하였으며, Fig. 12와 같이 음향 모드측정 결과 대비 유사한 모드 형상 해석 결과를 확인 할 수 있다. 거실 공간의 1차 음향 모드는 15 Hz, 2차 모드는 25 Hz로 분석되었으며, 거실 공간의 음장 분포를 결정하는 것은 거실 장축 방향의 axial mode인 2차 모드로 분석되었다⁽²²⁾. 결과적으로 전산해석을 이용하여 음향 해석 시 측정 결과 대비 유사한 해석 결과 도출이 가능할 것으로 판단된다.

Fig. 12

Mode shape of acoustic cavity (left: experimental results, right: numerical results)

5. 바닥충격음 예측 신뢰성 분석

5.1 바닥충격음 해석 모델 구성 및 예측

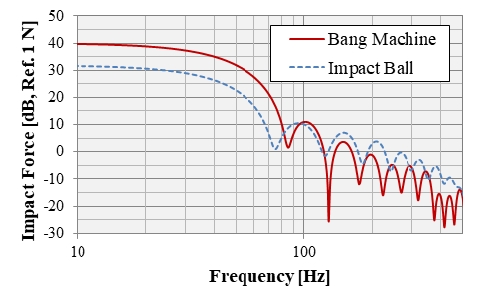
구조와 음향 모델을 개별적으로 구성하여 진동 및 음향 특성 분석을 수행하였으며, 측정 결과 대비 유사한 해석 결과를 도출 할 수 있는 것으로 분석되었다. 따라서 검증된 두 모델을 결합하여 바닥충격음 예측 모델을 구성하였으며, 해석 모델 구축 시 구조물과 음향 공간의 공유 면에 에너지 교환이 발생할 수 있도록 COMSOL의 “Acoustic-Structure Interaction” 모듈을 이용 하여 바닥충격음 해석 모델을 구성하였다. 바닥충격음 예측 시 하중 조건은 Fig. 13의 뱅머신과 고무공의 가진력 스펙트럼을 이용하였으며, 1 Hz 간격의 narrow band로 710 Hz까지 해석을 수행하였다.

Fig. 13

Force spectrum of bang machine and rubber ball

하중 조건은 바닥충격음 KSF 2810-1의 바닥충격음 측정 조건과 동일하게 5 지점에 하중 조건을 입력하였으며, 수음실 5 지점의 바닥충격음을 해석 결과를 산술평균하였다⁽²⁾. 해석 결과는 KSF 2863에 의거하여 1/3 옥타브 밴드로 변환하여 바닥충격음 측정 결과와 비교할 수 있도록 하였다.

5.2 바닥충격음 측정 및 신뢰성 분석

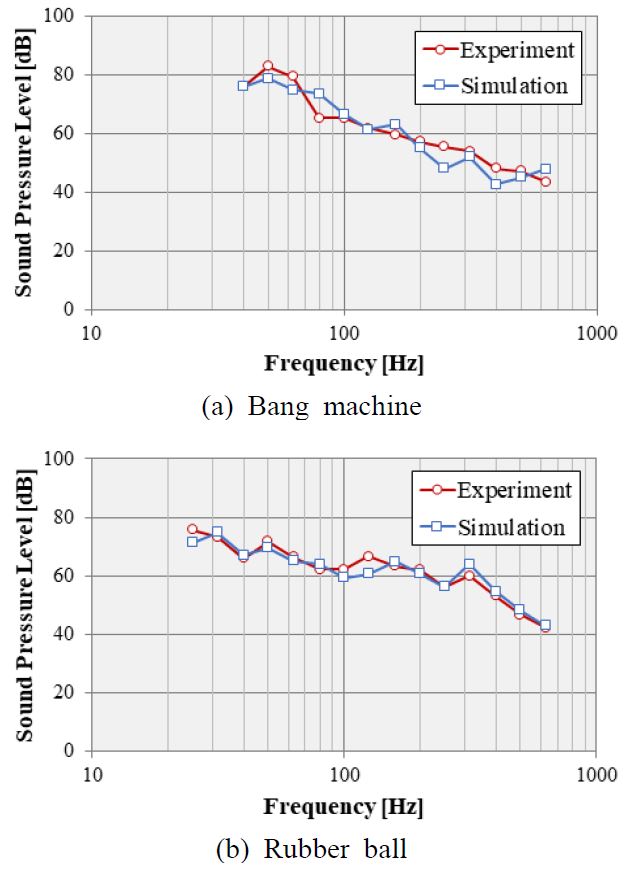
바닥충격음 해석 모델에 대한 신뢰성을 검증하기 위해 바닥충격음 해석 모델을 구성하였으며, 대상 실증주택의 거실공간에서 중량충격원에 대한 바닥충격음을 측정하였다. 바닥충격음 측정은 KSF 2810-1에 의거하여 측정하였다. KSF 2810-1에서는 중량충격음 측정 시 각 주파수 별 최대 소음도를 측정하도록 규정하고 있으나, 이 연구에서는 충격원에 의한 오차를 최소화 하기 위해 충격원 30회 가진 시 평균 응답을 측정하여 해석 결과와 비교 분석하였다. Fig. 14는 바닥충격음 측정을 위해 설치된 측정 장비를 나타낸다. Fig. 15는 바닥충격음 해석 및 측정 결과를 함께 도시화 하였다.

Fig. 14

View of test set-up

Fig. 15

Comparison of experimental and numerical results: 1/3 octave band

Fig. 15과 같이 유한요소법을 이용한 바닥충격음 해석 결과가 측정 결과와 비교하여 옥타브 별 소음도에서 뱅머신이 5 dB, 고무공이 4 dB 편차 범위 내에서 유사하게 분석되었으며, 충격원 변화에 따른 바닥충격음 변화 경향성 확인이 가능한 것을 알 수 있다.

Table 5는 중량충격음 해석 및 측정 결과에 대한 단일수치를 나타낸다. 현재, 국내 고시 상 중량충격음에 대한 단일수치 평가는 역A특성 가중 최대 음압레벨 (L_i,Fmax,AW)로 평가하고 있으며⁽²³⁾, ISO에서는 평가 주파수 대역은 동일하나 측정결과에 A가중치(A-weighting)를 적용한 후 전체 소음도(total sound pressure level)로 평가하는 A특성 최대 음압레벨 단일수치(L_iA,Fmax)로 평가하는 A특성 최대 음압레벨 단일수치(L_iA,Fmax) 평가방법을 도입을 검토 중에 있다⁽²⁴⁾. 표에서 확인할 수 있듯이 바닥충격음 예측 결과가 전체 소음도(L_iA,Fmax)에서 뱅머신이 2.1 dB, 임팩트볼이 0.5 dB 편차 범위로 분석되어 실제 측정 결과와 유사하게 분석되었다. 현재 바닥충격음 평가를 위해 사용되고 있는 단일수치량(L_i,Fmax,AW)에서는 뱅머신이 1 dB 편차범위, 고무공이 동일한 수치로 바닥충격음 차단성능 관련 고시에서 제시하는 바닥충격음 측정오차 수준으로 측정 결과와 유사하게 분석되었다. 결과적으로 전산해석을 이용한 바닥충격음 예측 시 콘크리트 재료의 비선형 특성으로 인해 피크 주파수에서 다소 차이가 발생할 수는 있지만, 전체 에너지 측면에서 유사한 해석 결과를 도출할 수 있는 것으로 분석되었다.

Table 5

Material property of acoustic model

6. 결 론

이 연구에서는 맨슬래브 조건의 벽식구조 실증주택을 대상으로 유한요소해석을 이용한 예측 모델링 정확도 검증 후, 중량충격원 종류 및 평가지표 변화에 따른 바닥충격음을 예측하였다.

바닥충격음 예측은 구조모델과 음향모델로 구성하였으며, 슬래브 진동 및 수음실 음향 특성을 측정하여 개별 해석 모델에 대한 검증을 수행하였다. 구조모델은 거실 공간을 대상으로 바닥 슬래브 모드 테스트를 수행하였으며, 진동 모드와 가속도 응답을 비교 분석하였다. 콘크리트 물성을 선형으로 가정하였기 때문에 진동 모드(피크 주파수)에서는 차이가 발생하였으나, 전체적인 에너지 측면에서는 유사하게 분석되었다. 음향 모델의 경우 거실 공간에 무지향 스피커로 음원을 발생시켜 음향 모드를 측정하였으며, 음향 모드의 경우 구조 모델에 비해 상대적으로 음향모드 주파수와 음압 크기에서 매우 유사하게 분석되었다. 결과적으로 개별적으로 구축된 구조모델과 음향모델을 이용하여 10 % 이내의 편차 수준에서 실제 진동 특성 및 응답 분석이 가능하였다.

검증된 해석 모델을 결합하여 바닥충격음 해석 모델을 구성하였으며, 중량충격원에 대한 바닥충격음을 분석하였다. 바닥충격음 해석 모델의 경우 평가대역 내 옥타브 별 최대 4 dB 편차가 발생하여 비교적 유사한 바닥충격음 분석이 가능하였으며, A특성 최대 음압레벨 단일수치(L_iA,Fmax)에 대해 뱅머신이 2.1 dB, 고무공이 0.5 dB 편차 범위로 매우 유사한 해석 결과를 도출하였다. 바닥충격음을 평가하기 위한 역A특성 가중 최대 음압레벨 (L_i,Fmax,AW)단일수치에 대해 뱅머신이 1 dB 편차범위, 고무공이 동일한 수치로 분석되어 전산해석을 이용한 바닥충격음 분석의 신뢰성을 검증하였다.

독립적인 구조 및 음향 모델에 대해 진동 및 음향 특성에 대한 오차를 저감하는 경우 보다 정밀한 바닥충격음 분석이 가능할 것으로 판단되며, 향후 전산해석을 이용하여 중량충격원 종류 및 평가방식 별 바닥충격음 저감을 위한 최적 구조 개발 등의 연구가 필요할 것으로 판단된다.

Acknowledgments

이 연구는 토지주택연구원에서 수행한 “공동주택 바닥충격음 저감 설계·시공 제어 요인 분석 연구(R201810001)" 결과의 일부임.

References

• Korea Environment Corporation, 2018, The Operating Report of Center for Floor Impact Noise Complaint Issues in Residential Buildings.
• Ministry of Land, Infrastructure and Transport, Acceptance and Management Standards for Floor Impact Sound Insulation Structures in Apartment Buildings, No. 2015-997.
• Jeong, J. H., 2019, Review and Perspective on the Researches of Floor Impact Sound, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 4, pp. 477~487. [https://doi.org/10.5050/KSNVE.2019.29.4.477]
• Kim, T. M., Kim, J. T. and Kim, J. S., 2018, Effect of Structural Vibration and Room Acoustic Modes on Low Frequency Impact Noise in Apartment House with Floating Floor, Applied Acoustics, Vol. 142, pp. 59~69. [https://doi.org/10.1016/j.apacoust.2018.07.034]
• Lee, B. K. and Koo, B. S., 2017, Prediction of Floor Impact Noise in Apartment by Finite Element Method. Proceedings of the KSNVE Annual Spring Conference, p. 34.
• Kim, M. J., Son, J. Y. and Kim, H. S., 1998, A Study on the Applicability of Statistical Energy Analysis (SEA) to Estimate the Light-weight Floor Impact Sound in Concrete Structures, Jounal of the Architectural Institute of Korea: Planning & Design, Vol. 14, No. 11, pp. 313~322.
• Mun, D. H., Lee, S. H., Hwang, J. S., Baek, G. O. and Park, H. G., 2015, Prediction of Heavy-weight Floor Impact Soundin Multi-unit House Using Finite Element Analysis, Journal of the Computational Structural Engineering Institute of Korea, Vol. 28, No. 6, pp. 645~ 658. [https://doi.org/10.7734/COSEIK.2015.28.6.645]
• Mun, D. H., Park, H. G. and Hwang, J. S., 2014, Prediction of Concrete Slab Acceleration and Floor Impact Noise Using Frequency Response Function, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 24, No. 6, pp. 483~492. [https://doi.org/10.5050/KSNVE.2014.24.6.483]
• István, L. V., 1971, Impact Noise Isolation of Composite Floors, The Journal of the Acoustical Society of America, Vol. 50, No. 4, pp. 1043~1050. [https://doi.org/10.1121/1.1912726]
• Hwang, J. S., Moon, D. H., Park, H. G., Hong, S. G. and Hong, G. H., 2010, The Effect of Dynamic Property of Absorbing Sheet on the Amplification of Heavy Weight Floor Impact Noise, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 7, pp. 651~ 657. [https://doi.org/10.5050/KSNVE.2010.20.7.651]
• Schiavi, A., Prato, A. and Belli, A. P., 2015, The “Dust Spring Effect” on the Impact Sound Reduction Measurement Accuracy of Floor Coverings in Laboratory, Applied Acoustics, Vol. 97, pp. 115~120. [https://doi.org/10.1016/j.apacoust.2015.04.011]
• István, L. V. and Beranek, L. L., 1992, Noise and Vibration Control Engineering: Principles and Applications, 1st Edition, Wiley-interscience, Hoboken, New Jersey.
• Chakraverty, S., 2009, Vibration of Plate, CRC Press, Boca Raton.
• Kim, Y. H., 2010, Sound Propagation: An Impedance Based Approach, John Wiley & Sons (Asia), Singapore. [https://doi.org/10.1002/9780470825853]
• Randall, R. B. and Tech, B. A., 1987, Frequency Analysis, Bruel & kjaer, Denmark.
• Kim, T. M., Kim, J. T. and Kim, J. S., 2018, SEA-FEM Hybrid Analysis for Predicting Inter-floor Impact Noise, Applied Acoustics, Vol. 129, pp. 397~407. [https://doi.org/10.1016/j.apacoust.2017.08.025]
• Ewins, D. J., 1984, Modal Testing: Theory and Practice, New York, Brisbane: Research Studies Press LTD, Research Stuclies Press LTD, Brisbane, New York.
• Malvar, L. J. and Ross, C. A., 1998, Review of Strain Rate Effects for Concrete in Tension, ACI Materials Journal, Vol. 95, pp. 735~739. [https://doi.org/10.14359/418]
• Ju, M. K., Han, M. H. and Oh, Y. K., 2009, Deviation of Sound Pressure Level Receiving Room According to the Heavy-weight Floor Impact Sources and It's Positions, Journal of Korea Institute of Ecological Architecture and Environment, Vol. 9, No. 4, pp. 23~28.
• Jung, J. Y., Lee, S. H., Jeong, G. C., Oh, Y. G. and Ju, M. G., 2005, A Study on the Effect by Receiving Points as Measuring Floor Impact Sound, Proceedings of the KSNVE Annual Spring Conference, pp. 283~286.
• International Organization for Standardization, 2010, Acoustics - Determination of Sound Power Levels and Sound Energy Levels of Noise Sources using Sound Pressure - Precision Methods for Reverberation Test Rooms, ISO 3741:2010.
• Lyon, R. H., 1987, Machinery Noise and Diagnostics, Butterworths, London. [https://doi.org/10.1016/B978-0-409-90101-6.50004-8]
• Korean Agency for Technology and Standards, Rating of Floor Impact Sound Insulation for Impact Source in Buildings and Building Elements - Part 1: Floor Impact Sound Insulation against Standard Heavy Impact Source, KS 2863-2:2017.
• Jeong, J. H., Park, S. H. and Lee, P. J., 2019, Single-number Quantities of Heavyweight Impact Sound Insulation, Acta Acustica United with Acustica, Vol. 105, No. 1, pp. 5~8. [https://doi.org/10.3813/AAA.919280]