이중 선형 감쇠특성을 갖는 새로운 형태의 MR 댐퍼 설계 및 해석

1. 서 론

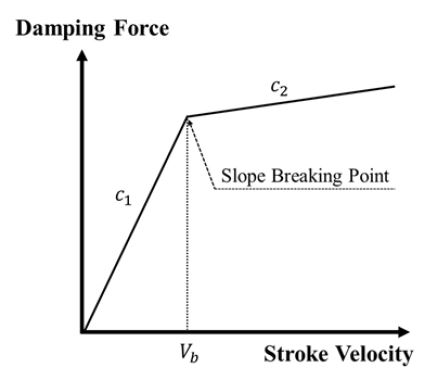
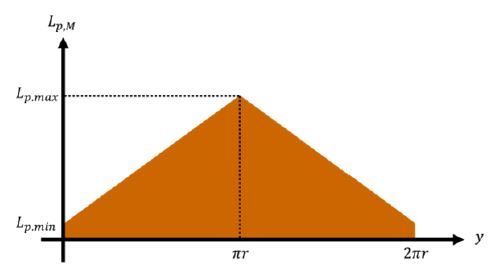
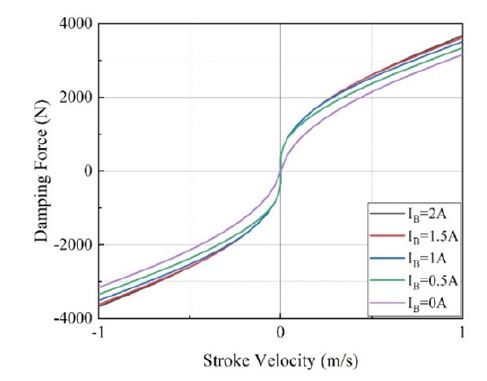
자동차 서스펜션 시스템의 주 역할은 차량의 무게지지뿐만 아니라, 도로 주행 시 바닥으로부터 전달되는 진동을 흡수하여 주행 성능을 향상시키는 것이다. 일반적으로 서스펜션 시스템은 탄성 요소인 스프링과 감쇠 요소인 댐퍼로 이루어진다. 이 때, 댐퍼는 차량의 주행 성능인 승차감과 조종 안정성에 결정적인 역할을 한다. 댐퍼의 종류로는 수동형 타입, 반능동형 타입, 그리고 능동형 타입이 있다. 수동형 댐퍼의 경우, 유체의 점성에 의해 발생하는 감쇠력을 이용하여 차체의 진동을 흡수한다. 주행 성능을 위하여 시행착오를 통해 수동형 댐퍼의 감쇠특성을 최적화하며, 시험적으로 얻은 최적의 감쇠 특성은 이중 선형 감쇠 특성을 가진다⁽¹⁾. 이 때, Fig. 1에 나타나 있듯이 이중 선형 감쇠 특성은 낮은 스트록(stroke) 속도에서 높은 감쇠계수, 높은 스트록 속도에서 낮은 감쇠계수를 갖는 감쇠 특성을 뜻한다. 그러나 수동형 댐퍼는 주행 환경에 따라 성능이 급격하게 감소하며, 잘 알려진 승차감과 조종 안정성 간의 트레이드 오프(trade-off) 관계를 충족시키는데 한계가 있다. 이러한 문제를 해결하기 위해 능동형 댐퍼와 반능동형 댐퍼가 연구되었다. 하지만 능동력 댐퍼의 경우 추가적인 하드웨어 및 복잡한 제어 로직이 요구되어 보편화에 어려움이 있다. 이러한 이유로 스마트 재료 중에 하나인 ER(electrorheological) 또는 MR(magnetorheological) 유체를 이용한 반 능동형 댐퍼가 많이 연구되었다^(2~6). 하지만, 일반적인 MR 댐퍼의 경우 불연속적이고 비선형적인 감쇠 특성을 가지며 스카이훅 제어, 퍼지 신경망 제어 등 피드백 기반의 제어 로직이 요구되는 한계가 있었다.

Fig. 1

Bilinear damping characteristic

이 연구에서는 오직 개루프 제어만을 통해 최적의 감쇠 특성 구현이 가능한 이중 선형 감쇠 특성을 갖는 극 형상 함수 기반의 새로운 형태의 MR 댐퍼를 제안한다. 제안된 MR 댐퍼는 이중 선형 감쇠 특성을 가짐으로써, 감쇠 특성의 불연속성과 비선형성을 보완한다. 또한, 구조적 특이성(극 형상)으로 인해 오직 개루프 제어만으로 이중 선형 감쇠 특성을 구현할 수 있다. 이어, 제안된 MR 댐퍼의 특징인 극 형상 함수를 고려하여 주 오리피스와 바이패스(bypass) 오리피스에 의해 발생하는 감쇠력을 수학적으로 모델링하였다. 최종적으로 감쇠력 해석을 통하여 제안된 댐퍼의 자기장 세기에 따른 이중 선형감쇠 특성을 분석하였다.

2. MR 댐퍼 구조 및 작동원리

2.1 댐퍼 형상

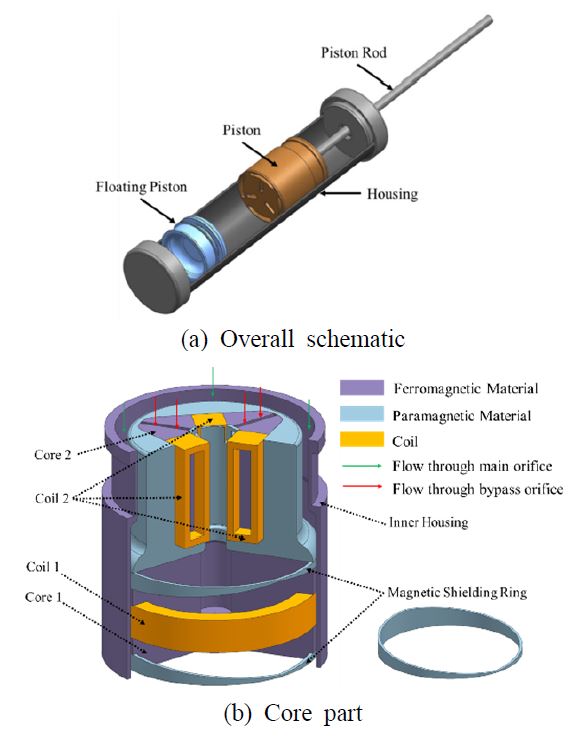
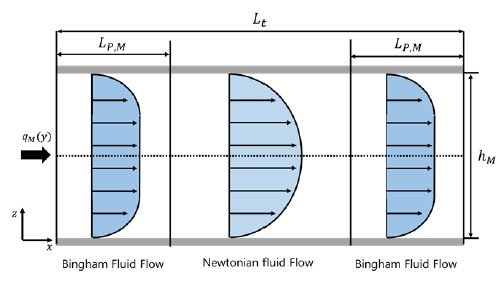
Fig. 2는 제안된 MR 댐퍼의 전체적인 개략도와 코어 부분의 형상을 나타낸다. MR 댐퍼는 피스톤 로드, 피스톤, 하우징 그리고 플로팅(floating) 피스톤으로 구성된다. 이는 일반적인 단일 튜브 타입 댐퍼로써 상부 챔버, 하부 챔버 그리고 공기 챔버로 이루어진다. 코어 부분은 감쇠계수 변화를 위한 환 형상의 주 오리피스와 기울기 변곡점 변화를 위한 직사각형의 세 개의 바이패스 오리피스를 가진다. MR 유체의 유동은 크게 주 오리피스 부분과 바이패스 부분으로 나누고, 각각은 제어를 위한 독립적인 코일을 가진다. 기존의 MR 댐퍼와 달리, 주 오리피스의 경우는 MR 효과가 발생하는 극 부분의 형상을 자기장 형성이 용이한 강자성체와 자기장 형성을 억제하는 상자성체를 혼합하여 설계하였다. 이로 인해, 유효 극은 원주 방향을 따라 다른 길이를 가지게 된다. 바이패스 오리피스의 경우는 일반적인 정사각형 형태의 MR 밸브 형상이며, 세 개의 바이패스 오리피스는 형상이 같다. 주 오리피스 부분과 바이패스 오리피스 부분의 독립적인 제어를 위해 상자성체를 이용하였으며, 두 제어부의 자기장 경로가 분리되도록 자기 회로를 설계하였다.

Fig. 2

Configuration of MR damper

2.2 작동 원리

MR 댐퍼의 감쇠력은 상부 챔버와 하부 챔버 사이의 압력 차에 의해 생성된다. 댐퍼 스트록으로 인해 좁은 유로를 통해 MR 유체가 흐르게 되며, 유체 점성과 자기장 인가에 따른 유체 항복 응력에 의한 압력 강하가 발생한다. 일반적인 MR 댐퍼의 경우에 자기장 인가 시 블락업(block-up)현상이 발생된다. 이 현상은 자기장에 의해 형성된 MR 유체의 철 입자 사슬이 유체의 유동을 막아 일어나는 현상으로, 피스톤의 왕복 운동 시 불연속적인 감쇠 특성을 유발하고 이는 댐퍼가 사용되는 시스템에 부정적인 영향을 끼치게 된다. 제안된 댐퍼의 경우 독립으로 제어되는 주 오리피스와 바이패스 오리피스를 가지므로, 두 오리피스에서 블락업 현상이 각각 일어날 수 있다. 하지만, 이중선형 감쇠특성을 가지게 되어, 피스톤 왕복 운동 시 연속적인 감쇠특성을 띄게 된다. 이중선형 감쇠특성의 경우 낮은 스트록 속도에서의 높은 감쇠계수와 특정 스트록 속도에서의 급격한 감쇠계수 변화를 특징으로 한다.

(1) 감쇠계수 변화

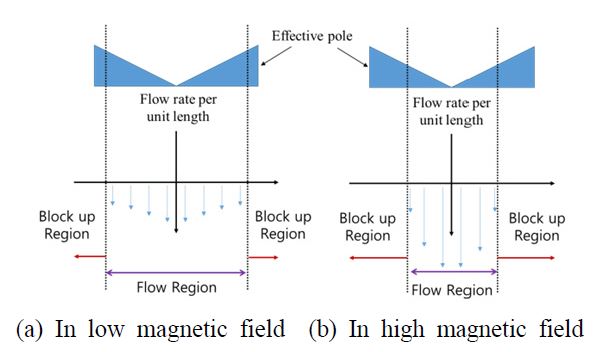
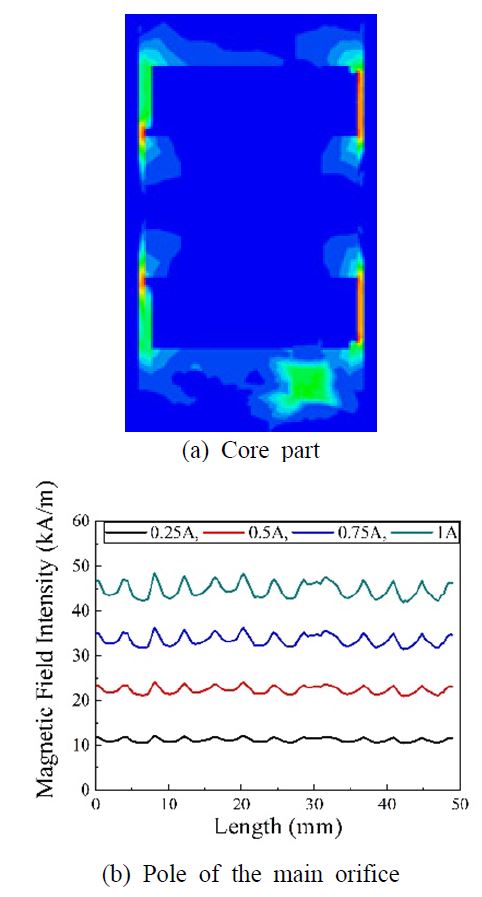
낮은 스트록 속도 구간에서의 감쇠계수 변화는 주 오리피스의 제어를 통해 구현된다. 주 오리피스의 특정 극 형상으로 인해, 자기장 인가에 따라 주 오리피스의 부분적인 블락업이 발생한다. 이를 통해, 주 오리피스의 유효 면적을 조절할 수 있고 결과적으로 감쇠계수 변화를 구현할 수 있다. Fig. 3은 자기장 세기에 따른 주 오리피스의 유량 분포를 나타낸다. 자기장 세기가 증가함에 따라 극 길이가 긴 부분에서부터 블락업 현상이 일어나며 부분적으로 유체가 흐름을 확인할 수 있다.

Fig. 3

Flow rate per unit length along the circumferential direction

(2) 기울기 변곡점 변화

특정 스트록 속도에서의 급격하게 감쇠계수가 변화하는 지점(기울기 변곡점)의 변화는 바이패스 오리피스의 개·폐 제어를 통해 구현된다. 즉, 바이패스 오리피스가 열리는 시점을 기울기 변곡점으로 정의한다. 저속 구간에서는 바이패스 오리피스 부분에 자기장을 인가하여 블락업 현상을 일으켜 주 오리피스만을 통해 유체가 흐르게 한다. 기울기 변곡점 이후에서는 주 오리피스 뿐만 아니라 바이패스 오리피스로도 유체가 흐르게 되며 전체적인 오리피스 유효면적이 넓어져 감쇠계수가 급격히 낮아지게 된다.

3. 수학적 모델링

스트록 속도와 감쇠력 사이의 관계를 도출하기 위해, 각 오리피스에 흐르는 MR 유체의 거동을 분석하였다. 일반적으로 MR 유체는 빙햄(Bingham) 유체로 모델링 된다⁽⁷⁾. 이 연구에서는 평판 유동 모델을 이용하여 유체 흐름 방향의 압력 강하만을 고려한 1차원 해석을 하였다^(8~11).

3.1 주 오리피스에서의 유체흐름

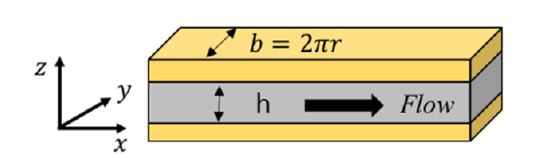
Fig. 4는 평판 유동 모델의 개략도와 좌표계를 나타낸다. 유체의 유동을 완전 발달 및 층류 유동으로 가정하였으며, 오리피스 내의 유동을 자기장의 영향이 없는 뉴토니안 유체 유동 구간과 자기장의 영향이 있는 빙햄 유체 유동 구간으로 나누어 해석하였다. Fig. 5는 제안된 댐퍼의 극 형상을 나타낸다. 극 형상을 수학적 방정식으로 나타낸 것을 극 형상 함수라 정의하고, 이 연구에서의 극 형상 함수는 식 (1)과 같다.

(1)

Fig. 4

Schematic configuration of parallel plate model and a coordinate system

Fig. 5

Pole shape function

여기서 L_p.max는 유효 극의 최대 길이, L_p.min은 유효 극의 최소 길이, r은 오리피스의 평균 반경이다. 이 때, 단위 단면에 대한 유효 극의 길이는 제안된 댐퍼의 특징인 극 형상에 따라 결정된다. Fig. 6은 주 오리피스의 단위 단면에서의 MR 유체의 거동을 나타내며, 주 오리피스에서의 압력강하 ∆P_t.M은 식 (2)와 같다.

$\[ ∆P_{t,M}={p^{\text{'}}}_{N,M}\left(L_{t,M}-2L_{P,M}\right)+2{p^{\text{'}}}_{y,M}{L}_{P,M} \]$

(2)

Fig. 6

Behaviors of MR fluid in main orifice

여기서 p^′_N.M은 뉴토니안 유체 유동에 의한 압력 강하 구배, p^′_y.M는 빙햄 유체 유동에 의한 압력 강하 구배, L_t.M는 오리피스의 총 길이, L_p.M는 유효 극의 길이이다. 이 때, 문제를 간단히 하고 파라미터화 하기 위하여, 식 (3)과 같은 무차원수를 사용하였다.

$\[ \begin{array}{c}\begin{array}{ccc}{{\rm N}}_M\triangleq \frac{{p^{\text{'}}}_{N,M}}{{p^{\text{'}}}_{C,M}},& {p^{\text{'}}}_{N,M}=\frac{12\eta }{h_M^3}q,& {p^{\text{'}}}_{C,M}=\frac{2{\tau }_{y.M}}{h_M}, \end{array}\\ \begin{array}{cc}{L}_M=\frac{L_{P,M}}{L_{t,M}},& P_{t,M}=\frac{∆P_{t,M}}{L_{t,M} {p^{\text{'}}}_{C,M}}\end{array}\end{array} \]$

(3)

여기서 η는 MR 유체의 점성 계수, q는 단위 길이에 따른 유량, h_M는 주 오리피스의 간극 크기, τ_y.M는 주 오리피스에서의 자기장에 따른 MR 유체의 항복응력, p^′_C.M는 빙햄 유체의 플러그(plug) 구간에서 발생하는 압력강하 구배, L_M은 유효 극의 길이에 대한 무차원수, P_t.M은 주 오리피스에서의 압력 강하 구배에 대한 무차원수이다. 이 때, 빙햄 유체 유동에 의한 압력강하 구배 p^′_y.M는 수치적 근사해를 사용하였다⁽¹²⁾. 식 (2)를 무차원수를 이용하여 나타내면 식 (4)와 같다.

$\[ P_{t,M}={{\rm N}}_M\left(1-2L_M\right)+2\left({{\rm N}}_M+1.035+\frac{{{\rm N}}_M}{2{{\rm N}}_M+0.4}\right)L_M \]$

(4)

위 식의 해는 다음과 같다.

$\[ \begin{array}{l}{{\rm N}}_M=\frac{-\left(0.4-2P_{t,M}+6.14L_M\right)}{4}\\ \frac{\pm \sqrt{{\left(0.4-2P_{t,M}+6.14L_M\right)}^2+3.2\left(P_{t,M}-2.07\right)L_M}}{4}\end{array} \]$

(5)

주 오리피스를 통한 전체 유량 Q_M은 유체가 흐르는 구간에 대하여 단위 길이에 대한 유량을 적분하여 얻을 수 있다. 블락업이 시작되는 지점 (y_b)은 전체 압력 강하가 빙햄유체 유동 구간에서의 압력강하와 같아 지는 지점이며, 따라서 블락업을 고려하였을 때의 전체 유량은 식 (6)과 같이 구할 수 있다.

(6)

여기서 L_b는 블락업이 발생하는 단면에서의 유효 극의 길이이다.

3.3 두 오리피스를 통한 전체 유체흐름

지금까지 각 오리피스를 통한 유체의 거동을 독립적으로 분석하였다. 하지만, 주 오리피스와 바이패스 오리피스에 인가되는 자기장의 세기에 따라 여러 형태의 유동 모드가 발생한다. 유동 모드는 세 개의 임계 압력 강하 값에 따라 결정된다. 임계 압력 강하는 오리피스의 개폐를 판단하는 기준이 되며, 식 (4)와 식 (7)에서 유량이 0인 경우로써 오직 MR 유체의 항복응력에 의해 발생하는 압력 강하를 의미한다.

$\[ ∆P_{c,M1}=2.07\bullet \frac{2{\tau }_{y,M}{x}_m}{h_M} \]$

(8)

$\[ ∆P_{c,M2}=2.07\bullet \frac{2{\tau }_{y,M}{L}_{p,\mathrm{m}\mathrm{a}\mathrm{x}}}{h_M} \]$

(9)

$\[ ∆P_{c,B}=2.07\bullet \frac{{\tau }_{y,B}{L}_{P,B}}{h_B} \]$

(10)

여기서 ∆P_c,M1는 주 오리피스가 부분적으로 열리게 되는 압력 강하, ∆P_c,M2는 주 오리피스가 완전히 열리게 되는 압력 강하, ∆P_c,B는 바이패스 오리피스가 열리게 되는 압력강하이다. Table 1은 임계 압력 강하 값에 따른 유동 모드들을 나타낸다. 유체의 질량 보존에 의거한 연속방정식을 토대로 총 유량 Q_total과 총 압력강하 ∆P_total 사이의 구성방정식은 식 (11)과 식 (12)와 같다.

$\[ Q_{total}=Q_M+Q_B \]$

(11)

$\[ ∆P_{total}=∆P_M=∆P_B \]$

(12)

Table 1

Several types of flow mode

4. 감쇠력 해석

MR 댐퍼의 감쇠력은 상·하부 챔버의 압력 차이로 생성된다. 댐퍼가 준 정적 거동을 하고 기계적 마찰력을 무시한다고 가정할 때, MR 댐퍼가 받는 힘 F_total은 식 (13)과 식 (14)와 같다.

여기서 P₁은 상부 챔버의 압력, P₂는 하부 챔버의 압력, A_p는 피스톤 면적, A_r은 피스톤 로드의 면적, P_a는 공기 챔버의 압력이다. MR 댐퍼가 받는 힘 F_total은 감쇠력 F_d과 공기 스프링력 F_air으로 이루어 진다.

해석에 사용된 설계 파라미터는 Table 2와 같다. Fig. 7은 코어부의 자기장 해석 결과를 나타낸다. 자기장 해석에 따르면, 두 제어부를 독립적으로 제어할 수 있으며, 주 오리피스 제어부에 전류 인가 시 주 오리피스의 극 길이에 상관없이 유효 극에는 일정한 자기장이 형성됨을 알 수 있다.

Table 2

Design parameters of MR damper

Fig. 7

Magnetic field analysis

4.1 감쇠계수 제어

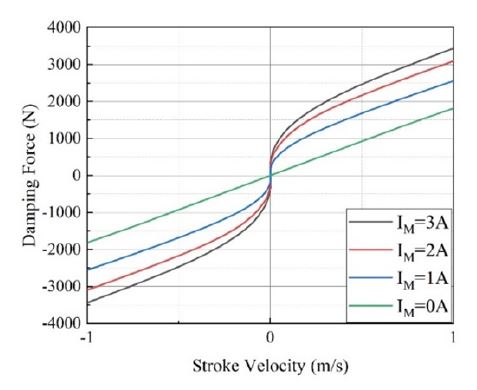
감쇠계수 변화는 주 오리피스 제어부에 전류를 인가하여 유효 면적을 조절함으로써 구현할 수 있다. Fig. 8은 주 오리피스의 제어부에 인가 전류 I_M을 1 A 간격으로 증가 시켰을 때의 감쇠특성을 나타내며, 이 때, 바이패스 제어부에 인가된 전류 I_B는 일정하다. I_M이 증가할수록 기울기 변곡점 이전의 기울기가 상승하는 것을 확인할 수 있다. 또한, 감쇠특성은 디그레시브(degressive) 감쇠 형태를 보임을 알 수 있다. 이때, 선형 감쇠 특성을 평가하기 위하여, 등가 감쇠계수를 기울기 변곡점까지의 선형 기울기라고 정의하였다. 기울기 변곡점 이전 구간에서의 등가 감쇠계수는 I_B가 0.75 A로 일정하고 I_M가 0 A, 1 A, 2 A, 그리고 3 A일 때, 각각 1600 N·s/m, 4232 N·s/m, 8701 N·s/m, 12 846 N·s/m이다. 넓은 범위의 감쇠계수 구현이 가능하지만, 높은 감쇠계수를 구현할수록 구현 가능한 스트록 속도범위가 감소하는 것을 알 수 있다.

Fig. 8

Damping coefficient control

4.2 기울기 변곡점 제어

기울기 변곡점 변화는 바이패스 오리피스 제어부에 전류를 제어하여 유로 개·폐를 조절함으로써 구현할 수 있다. Fig. 9은 바이패스 오리피스의 제어부에 인가 전류 I_B를 0.5 A 간격으로 증가시켰을 때의 감쇠특성을 나타내며, 이 때의 I_M은 3 A로 일정하다. I_B가 0.5 A, 1 A, 1.5 A, 그리고 2 A일 때, 각각의 기울기 변곡점에서의 감쇠력 크기는 863 N, 1722 N, 2486 N, 3100 N이다. 전류가 증가함에 따라 기울기 변곡점이 상승함을 알 수 있고, 이를 통해 감쇠계수 제어를 통해 결정된 저속에서의 높은 감쇠계수의 구현 스트록 구간을 조절할 수 있음을 알 수 있다.

Fig. 9

Slope breaking point control

4.3 요구 감쇠 특성 제어

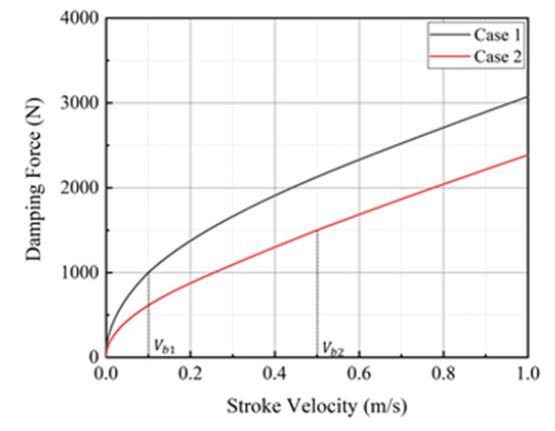
앞에서의 감쇠계수 제어와 기울기 변곡점 제어를 기반으로 제안된 MR 댐퍼는 제어 영역 내의 어떠한 요구 이중 선형 감쇠 특성도 개루프 제어만을 통해 구현 가능하다. Fig. 1의 이중 선형 감쇠 특성에서 c₁은 기울기 변곡점 이전의 높은 감쇠계수, c₂는 기울기 변곡점 이후의 낮은 감쇠계수, 그리고 V_b는 기울기 변곡점에서의 스트록 속도를 나타낸다. 이 연구에서는 임의의 요구 감쇠특성을 정하여 주 오리피스와 바이패스 오리피스 제어부의 개루프 제어만을 통해 요구하는 댐핑력을 구현하였다. Table 3은 두 경우의 요구 감쇠 특성 파라미터 값 c₁, V_b과 요구 인가 전류 I_M, I_B를 나타낸다. Case 1의 경우, c₁과 V_b1가 각각 10 000 N·s/m, 0.1 s/m이며, 요구 인가 전류 I_M과 I_B가 각각 2.42 A, 0.58 A이다. Case 2의 경우, c₁과 V_b2가 각각 3000 N·s/m, 0.5 s/m이며, 요구 인가 전류 I_M과 I_B가 각각 0.78 A, 0.87 A이다. 제안된 MR 댐퍼를 이용하여 요구 감쇠 특성을 구현한 결과는 Fig. 10과 같다. 이를 통해, 제안된 MR 댐퍼는 오직 개루프 제어만으로 요구 이중 감쇠특성을 구현함을 알 수 있다.

Table 3

Required input current IM and IB for implementing some desired c1 and Vb

Fig. 10

Desired damping characteristic

5. 결 론

이 연구는 이중 선형 감쇠 특성을 갖는 극 형상함수 기반의 새로운 형태의 MR 댐퍼를 제안한다. 제안된 댐퍼의 특징인 극 형상 함수를 고려하여, 수학적 모델링을 수행하였다. 이어 감쇠력 해석이 진행되었다. 해석 결과에 따르면, 이중 선형 감쇠 특성을 결정 짓는 감쇠계수와 기울기 변곡점을 오직 개루프 제어를 통해 구현 가능함을 확인하였다. 감쇠계수의 경우 주 오리피스 제어부의 인가 전류를 증가함에 따라 등가 감쇠계수가 1600 N·s/m에서 12 846 N·s/m까지 변화하였다. 또, 기울기 변곡점 제어의 경우 바이패스 오리피스 제어부의 인가 전류를 증가함에 따라 기울기 변곡점에서의 감쇠력 크기가 863 N에서 3100 N까지 증가하였다. 제안된 MR 댐퍼는 구조적 특이성(극 형상)으로 인해 이중 선형 감쇠 특성을 가짐으로써 기존의 MR 댐퍼의 불연속적인 감쇠력을 보완하였다. 또, 주 오리피스와 바이패스 오리피스를 각각 독립적으로 제어하여 감쇠계수 및 기울기 변곡점을 조절함으로써 제어 영역 내의 어떠한 이중 선형 감쇠 특성도 구현 가능함을 확인하였다.

References

• Fukushima, N., Hidaka, K. and Iwata, K., 1983, Optimum Characteristics of Automotive Shock Absorbers under Various Driving Conditions and Road Surfaces, International Journal of Vehicle Design, Vol. 4, No. 5, pp. 463~472.
• Kim, W. H., Hwang, Y. H., Park, J. H., Shin, C. S. and Choi, S. B., 2017, Performance Evaluation of a Quarter Car Suspension System Installed with MR Damper Featuring Bypass Flow Holes in Piston, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 1, pp. 65~71. [https://doi.org/10.5050/KSNVE.2017.27.1.065]
• Yao, G. Z., Yap, F. F., Chen, G., Li, W. and Yeo, S. H., 2002, MR Damper and Its Application for Semi-active Control of Vehicle Suspension System, Mechatronics, Vol. 12, No. 7, pp. 963~973. [https://doi.org/10.1016/S0957-4158(01)00032-0]
• Nguyen, Q. H. and Choi, S. B., 2009, Optimal Design of MR Shock Absorber and Application to Vehicle Suspension, Smart Materials and Structures, Vol. 18, No. 3, p. 035012. [https://doi.org/10.1088/0964-1726/18/3/035012]
• Lu, S. B., Li, Y. N., Choi, S. B., Zheng, L. and Seong, M. S., 2011, Integrated Control on MR Vehicle Suspension System Associated with Braking and Steering Control, Vehicle System Dynamics, Vol. 49, No. 1-2, pp. 361~380. [https://doi.org/10.1080/00423110903401889]
• Yu, M., Choi, S. B., Dong, X. M. and Liao, C. R., 2009, Fuzzy Neural Network Control for Vehicle Stability Utilizing Magnetorheological Suspension System, Journal of Intelligent Material Systems and Structures, Vol. 20, No. 4, pp. 457~466. [https://doi.org/10.1177/1045389X08091972]
• Carlson, J. D. and Jolly, M. R., 2000, MR Fluid, Foam and Elastomer Devices, Mechatronics, Vol. 10, No. 4-5, pp. 555~569. [https://doi.org/10.1016/S0957-4158(99)00064-1]
• Phillips, R. W., 1969, Engineering Applications of Fluids with a Variable Yield Stress, Doctoral Dissertation, University of California, Berkeley.
• Gavin, H. P., Hanson, R. D. and Filisko, F. E., 1996, Electrorheological Dampers, Part I: Analysis and Design, Journal of Applied Mechanics, Vol. 63, No. 3, pp. 669~675. [https://doi.org/10.1115/1.2823348]
• Stanway, R., Sproston, J. L. and El-Wahed, A. K., 1996, Applications of Electro-rheological Fluids in Vibration Control: A Survey, Smart Materials and Structures, Vol. 5, No. 4, p. 464. [https://doi.org/10.1088/0964-1726/5/4/011]
• Wereley, N. M. and Pang, L., 1998, Nondimensional Analysis of Semi-active Electrorheological and Magnetorheological Dampers Using Approximate Parallel Plate Models, Smart Materials and Structures, Vol. 7, No. 5, p. 732. [https://doi.org/10.1088/0964-1726/7/5/015]
• Yang, G., Spencer Jr, B. F., Carlson, J. D. and Sain, M. K., 2002, Large-scale MR Fluid Dampers: Modeling and Dynamic Performance Considerations, Engineering Structures, Vol. 24, No. 3, pp. 309~323. [https://doi.org/10.1016/S0141-0296(01)00097-9]