유체-구조 연성을 고려한 기저막 운동에서 와우공 크기의 영향

1. 서 론

사람의 귀는 크게 외이, 중이와 내이로 나뉘어지는데 와우는 그 중 내이에 해당하는 청각기관이다. 와우는 유체로 채워진 3개의 통로 전정계(scala vestibuli, SV), 고실계(scala tympani, ST)와 중간계(scala media, SM)로 구성되어 있다. 중앙에 위치하는 중간계는 라이스너막(reissner membrane, RM)에 의해 전정계와 분리되고 기저막(basilar membrane, BM)에 의해 고실계와 분리된다. 기저막은 길이 방향에 따라 폭과 넓이가 변하고 다르게 진동함으로써 소리 신호를 구별한다. 진동에 의해 막 위의 청세포가 움직여 중이로부터의 기계적 운동이 전기적 신호로 변환된다^(1~4). 음의 높낮이는 기저막에 청각세포의 위치에 따라 구분되며 일반적인 사람의 경우 청각세포는 20 Hz ~ 20000 Hz 정도의 소리진동을 느낄 수 있다. 와우공이 존재하는 기저막의 첨단부로 갈수록 저주파 영역의 소리를 인식하게 되는데, 와우의 끝에 위치하는 작은 구멍인 와우공(helicotrema)이 저주파 영역에 영향을 미친다고 알려져 있다. 와우공은 ST와 SV사이에 유체가 자유롭게 오갈 수 있도록 두 개의 와우 관을 연결한다. 정적인 측면에서 ST와 SV의 압력은 와우공으로 인해 서로 동일하다. 또한 와우공은 와우의 동적 응답에 큰 영향을 미친다. 그러나 와우공의 동적 역할은 아직 정량적으로 확인되지 않았다.

과거의 연구들 중 Puria와 Allen⁽⁵⁾은 와우공이 낮은 주파수에서만 와우의 입력 임피던스(input impedance)에 큰 영향을 미친다는 것을 보여주었고, Mountain⁽⁶⁾의 연구는 쥐, 친칠라, 고양이, 쇠돌고래의 와우공 치수와 차단 주파수(cutoff frequency)를 측정하고 정리하였다. 그리고 Li fu Xu et. al⁽⁷⁾은 와우공 크기를 고려한 인간 와우의 유한요소(finite element, FE) 모델을 만들어 BM의 피크(peak) 크기를 비교하였다. 이러한 연구들은 와우공의 크기가 와우의 진동특성에 영향을 미친다는 것을 보여 주었다.

이 연구에서는 앞서 언급한 연구 결과를 충분히 고려하고, 와우의 특징과 이전 연구 결과에 기초하여, 와우공의 크기가 와우에 미치는 영향을 정량적으로 확인한다. 와우의 동특성의 변화는 이전 연구에서 개발한 BM의 횡등방성(transverse isotropic) 특성을 고려한 유체-구조 연성 유한요소 해석 모델⁽⁸⁾을 기반으로 하여 와우공의 크기를 변화시켜 관찰하였다. 이 모델을 사용하여 와우의 동적 응답을 계산하고, 와우공 크기의 영향을 와우의 입력 임피던스 측면에서 살펴본다.

2. 와우의 유한요소 해석 모델

2.1 유한요소 해석 직선 모델

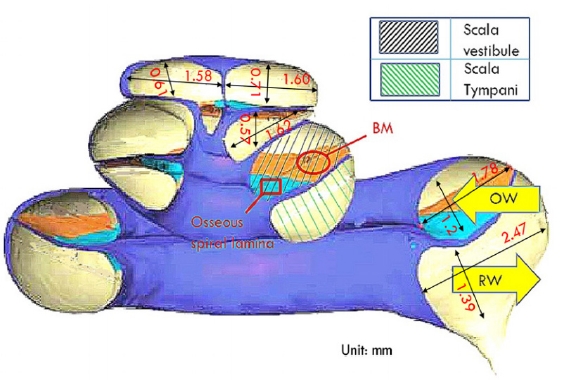
인간의 와우는 Fig. 1과 같이 나선형 형상⁽⁹⁾을 가지고 있다. 와우의 동특성을 해석하기 위하여 이전 연구에서 개발한 직선 모델을 이용하였다. 이 모델은 BM과 유체의 상호작용을 고려하고 BM의 횡등방 물성⁽¹²⁾을 고려한 유한요소모델로 자세한 사항은 이전 연구를 참조한다⁽⁸⁾. Diependaal과 Viergever⁽¹³⁾, Steele과 Zais⁽¹⁴⁾는 적분방정식을 이용한 해석적 모델을 통해 나선형 와우와 직선형 와우의 BM 속도에 의미 있는 차이는 없다고 결론지었지만 또 다른 연구에서는 나선형의 형상이 중요한 영향을 미친다는 사실을 보고하기도 하였다⁽¹⁵⁾. 이 연구에서는 우선 직선형 모델을 사용하여 와우공의 영향을 비교해 보고자 하였다.

Fig. 1

Three-dimensional cochlea of human

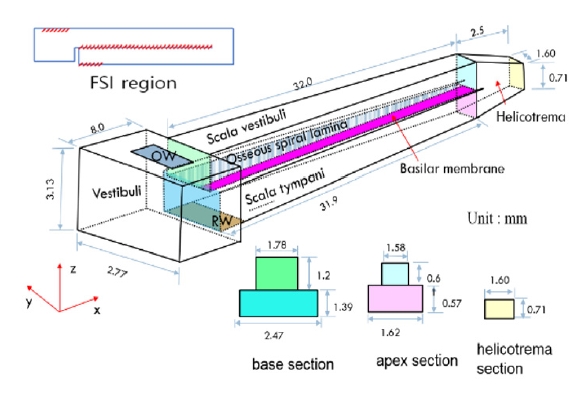
직선 모델은 와우의 동특성에 영향이 적으면서도 모델링이 간단하다는 장점이 있다. Fig. 2는 사용된 와우 FE 모델의 형상을 나타내었다. 이는 μCT⁽⁹⁾를 사용하여 사후의 54세 여성의 측두골을 촬영한 Fig. 1 모델의 통로 길이를 참조하여 와우의 기하 특성을 모델링하였다. FE 모델은 직선 형태의 직사각형 관으로 BM, 골나선판(osseous spiral lamina, OSL), 난원창(oval window, OW), 정원창(round window, RW)과 와우의 유체로 구성되어 있다. SV와 ST라 불리는 관은 내부가 림프액으로 가득 채워져 있는데 이 유체는 와우공을 통해서 연결되며 OSL과 BM으로 분리되어 있다. SV와 연결되어 있는 OW는 중이 등골의 운동을 내이로 전달한다. ST와 연결되어 있는 RW는 중이강과 통하여 내이 유체파동 압력을 이완시키는 상호작용을 담당한다. BM은 길이가 32 mm이며 횡등방성을 갖는다. FE 모델의 물성치는 Tables 1, 2에 따라 입력되었다.

Fig. 2

Dimensions of FE model of the uncoiled cochlea

Table 1

Several types of flow mode

Table 2

Material properties of cochlea fluid

BM, OSL의 양면과 OW와 RW는 와우의 유체와 접촉하여 연성 운동을 한다. 유체-구조 연성해석은 이전 연구⁽⁸⁾에서 얻은 식 (1)을 사용하였다.

$\[ \left[\begin{array}{cc}{M}_s& 0\\ -A^T& M_f\end{array}\right]\left\{\begin{array}{c}{\ddot{u}}_s\\ \ddot{p}\end{array}\right\}+\left[\begin{array}{cc}{B}_s& 0\\ 0& B_f\end{array}\right]\left\{\begin{array}{c}{\dot{u}}_s\\ \dot{p}\end{array}\right\}+\left[\begin{array}{cc}{K}_s& A\\ 0& K_f\end{array}\right]\left\{\begin{array}{c}{u}_s\\ p\end{array}\right\}=\left\{\begin{array}{c}{F}_s\\ F_f\end{array}\right\} \]$

(1)

식 (1)의 [M_s], [B_s], [K_s]는 구조물의 질량, 감쇠 및 강성 행렬을 나타내며 [F_s]는 구조물에 작용하는 외력벡터이다. [M_f], [B_f], [K_f]는 유체의 질량, 감쇠 및 강성 행렬을 나타내며 [A]는 구조와 유체의 연성행렬이다. {p}, {u_s}는 절점에서의 음압과 변위벡터를 나타내고 {F_f}는 유체에 작용하는 외력벡터이다.

와우공의 크기는 그 변동성이 크지만 유한요소 모델에서는 단면적을 1 mm² ~ 2 mm²으로 모델링 하였다^(18~20). 최근 연구에서는 다수의 인체에 대하여 와우공의 크기를 측정한 결과 BM 끝단에서 첨단부까지의 길이가 1.6 ∓ 0.9 mm로 나타났다⁽²¹⁾. 이 연구에서는 Fig. 2와 같이 이 길이는 2.5 mm로 고정하고 BM과 수평인 면을 OSL로 차폐하면서 와우공의 크기를 변화시켰다. 개발된 FE 모델을 이용하여 와우공 크기를 점차 줄여가면서 와우공의 크기가 와우의 동특성에 미치는 영향을 평가하기 위하여 와우의 입력 임피던스를 계산하였다. FE 모델에서 와우의 크기를 줄이기 위해, OSL과 BM의 끝 가장자리를 OSL과 동일한 물성을 사용하여 정점 영역의 끝까지 수평으로 확장하였다. 확장된 영역의 가장자리에 있는 모든 병진 변위들(translational displacements)은 고정하였다. 또한 확장된 영역은 양면이 와우의 유체와 접촉하고 있다.

유한요소 모델의 해석을 위해 상용 소프트웨어인 MSC/NASTRAN⁽¹⁰⁾을 이용하였다.

2.2 와우의 입력 임피던스

포유류에서 청력의 저주파 및 중주파 영역은 중이 전달 기능, 즉, 등자뼈 부근과 고막의 압력의 비에 의해 강한 영향을 받는다. 이 전달 함수의 동작은 중이의 컴플라이언스(compliance)와 와우의 입력 임피던스 사이의 상호작용에 의해 형성된다. 와우 입력 임피던스의 중주파수 영역은 유체의 관성력과 기저막의 컴플라이언스에 의해 지배되고, 저주파수 영역은 와우공에 의해 영향을 받는다^(5,16,17). 따라서 와우의 입력 임피던스는 중이를 통한 와우로의 소리 에너지 전달에 대해 이해하고 와우 모델의 개발과 검증 시 중요한 변수이다.

와우 임피던스는 중이 끝에 가해지는 와우의 전체 하중을 나타내며 식 (2)와 같이 표현된다.

$\[ Z_c=\frac{p_{ow}}{V_{ow}} \]$

(2)

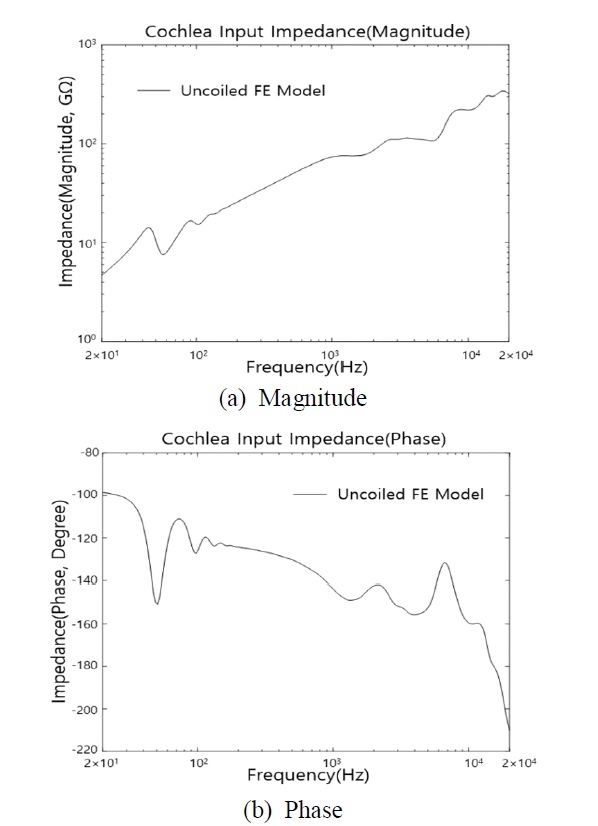
위 식에서 p_ow은 OW의 표면 압력을 나타내고 V_ow는 OW의 체적 속도이다. 와우의 입력 임피던스를 계산하기 위해 OW의 경계 부분에 대하여 3방향 변위를 고정하고 등골근에서 전달되는 입력을 가정하여 OW 전체에 수직방향의 균일한 단위 속도를 조화 가진으로 적용하였다. 유한요소 모델 해석을 통해 OW의 표면 압력을 구하고 창 영역에 대해 평균값을 사용하였다. Fig. 3은 기준 와우공 크기(최대 단면적)일 때의 와우 입력 임피던스를 보여준다. Fig. 3의 입력 임피던스는 해석을 통해 관심 주파수 영역(20 Hz ~ 20 kHz)에서 OW의 표면 압력을 고정된 OW의 체적 속도로 나눈 값을 구한 것이다. Fig. 3에서 볼 수 있듯이 주파수가 증가하면 와우의 입력 임피던스가 증가한다. 그러나 골짜기처럼 공진과 연관된 와우 입력 임피던스의 몇몇 하락하는 구간도 나타난다. 이 골짜기는 아직 생성 원인이 불분명하다.

Fig. 3

Cochlea input impedance with the maximum helicotrema size

3. 해석 결과 및 토의

3.1 와우의 입력 임피던스 변화

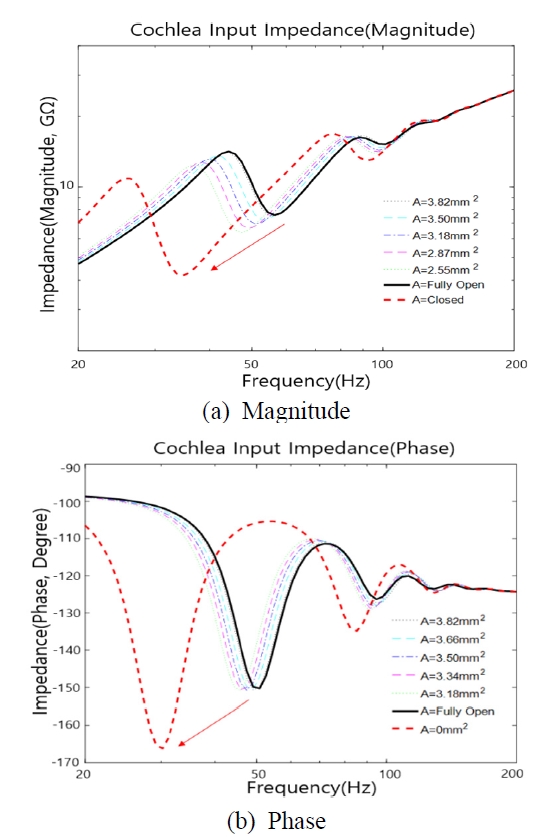
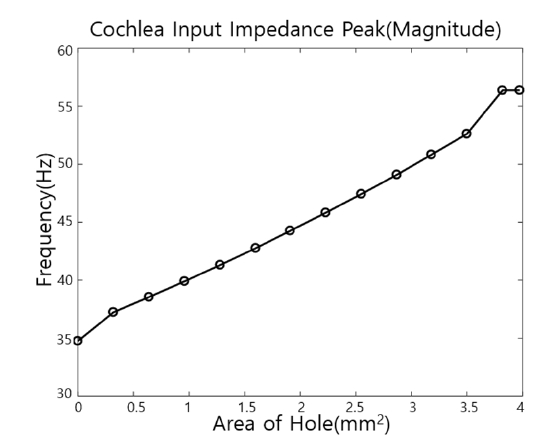
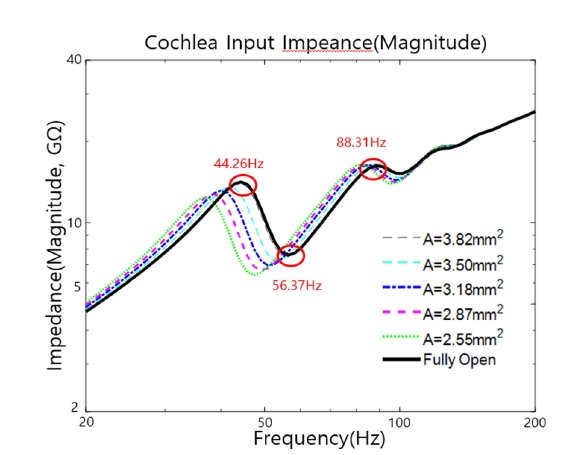
와우 FE 모델을 사용하여 와우의 입력 임피던스에 대해 와우공 크기가 미치는 영향을 살폈다. 와우공의 크기는 와우공의 단면적을 대표값으로 표기하였으며 최대 와우공 크기일 때 단면적은 3.975 mm²이고 완전히 닫혔을 때의 단면적은 0이다. Fig. 4는 와우공의 크기에 따른 와우의 입력 임피던스 변화를 보여준다. 그림에서 와우공의 크기는 와우공의 단면적을 대표값으로 표기하였다. Fig. 4에서 보듯이 와우공 크기의 영향은 200 Hz 미만에서만 나타났으며 그 이상의 주파수 영역에서는 변화가 없었다. Fig. 4(a)에서 보듯이 200 Hz 미만에 위치한 와우의 입력 임피던스의 골은 와우공의 크기가 작아질수록 저주파 방향으로 이동하였다. 이는 와우의 입력 임피던스에서 와우공 크기의 감소에 따라 공진 피크가 낮아지는 것을 보여준다. Fig. 4(b)에서는 위상이 골짜기 부근에서 급격한 변화를 가지고 있음을 확인할 수 있다. Fig. 5에 와우공 크기의 변화에 따른 와우의 입력 임피던스 그래프의 첫 번째 골의 위치를 보였다. Fig. 5를 통해 첫 번째 골의 위치가 와우공 단면적에 거의 비례하는 것을 알 수 있다. 따라서 와우공의 크기를 조절 및 변경하여 골짜기 위치를 조절하는 것이 가능할 수 있다. 단, 저주파 영역에서 음향 전달(sound transmission)의 전체 임피던스는 등자뼈(stapes)의 질량에 크게 의존한다는 사실에 유의해야한다⁽¹¹⁾. 즉, 등자뼈의 질량이 충분히 작으면 저주파 영역의 음향 전달이나 청각 민감도에 있어서 와우의 입력 임피던스의 첫 번째 위치가 중요하게 된다. 저주파 영역에서만 와우의 크기가 와우의 입력 임피던스에 큰 영향을 미치는 계산 결과는 이전의 연구⁽⁵⁾와도 잘 일치한다.

Fig. 4

Changes of the cochlea input impedance according to helicotrema sizes

Fig. 5

First valley locations in the cochlear input impedance according to helicotrema sizes

그러나 이 연구의 FE 모델에서는 와우 유체의 점성으로 인한 와우공에서 손실은 전체적으로 등가 감쇠로 처리되었고 국소적인 경계층 영향은 고려되지 않았다.

3.2 와우의 동적 운동

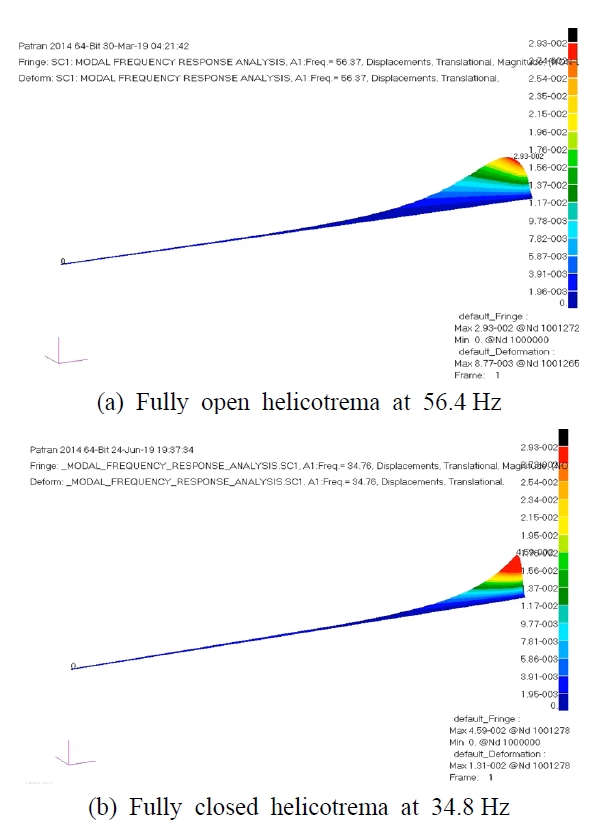
와우공이 와우의 입력 임피던스에 미치는 영향을 이해하기 위해 와우공의 크기를 입력 임피던스에 가장 큰 차이를 보이는 완전 개방과 완전 폐쇄 두 상태에 대해 첫 번째 골짜기 주파수에서 와우의 움직임을 관찰했다. Fig. 6(a)는 와우공 크기를 완전히 개방한 상태에서 골짜기 위치인 56.4 Hz에서 와우의 압력 분포를 보여준다. Fig. 6(b)는 와우공 크기를 완전히 폐쇄한 상태에서 골짜기 위치인 34.8 Hz에서 와우의 압력 분포를 보여준다. Fig. 6에서 완전히 개방한 와우공이 더 큰 압력 크기를 가지고 있지만, 압력 분포에는 근본적인 차이가 없음을 확인했다. Fig. 7은 Fig. 6에서와 동일하게 완전 개방 및 완전 폐쇄 각각의 주파수에서 BM의 해당 움직임을 보여준다. Fig. 7(b)의 완전히 폐쇄한 와우공일 때, BM의 움직임에서 진폭이 더 컸다. 하지만 이 또한 BM의 압력 분포와 운동에는 근본적인 차이가 없었다. 이를 통해 피크 위치가 이동하는 것이 동특성과 관련 있다고 추측하고 있지만 두 주파수가 공진 현상인지는 아직 불분명하다.

Fig. 6

Pressure distributions of cochlea

Fig. 7

Deformations of the basilar membrane

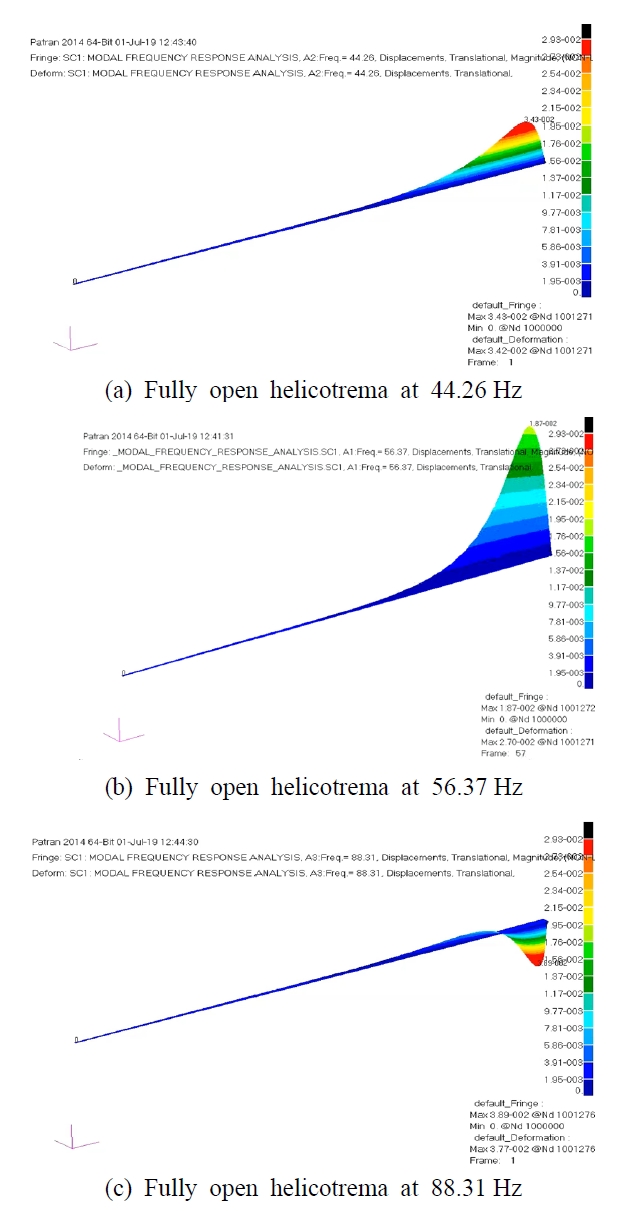
골짜기 형성의 원인을 확인하기 위해 완전 개방한 와우공을 Fig. 8과 같이 44.26 Hz, 56.37 Hz, 88.31 Hz 세 지점에서 와우의 OW 표면 압력 분포를 비교하였다. 하지만 56.37 Hz에서 OW의 최대압력이 다른 두 지점과 비교했을 때 작아지는 특별한 이유는 발견하지 못했다. 대신 Fig. 9와 같이 BM의 변위에 차이가 있음을 확인했다. Fig. 9(a)의 44.26 Hz에서 BM은 위 아래의 움직임만을 가지고 있었고, Fig. 9(b)의 55.37 Hz에서 BM은 더 크게 위 아래로 움직이면서 위상 변화를 가지고, Fig. 9(c)의 88.31 Hz에서 BM은 작은 상하 방향의 움직임을 가지지만 더 확실한 위상변화를 가지는 것을 알 수 있었다. 최대 변위에서 공진을 나타내는 위상 변화를 볼 수 있다. 이는 구조 부분에서뿐만 아니라 유체 부분에서도 관련이 있는 것은 분명하다. 이를 확인하기위해 유체-구조를 고려한 복소 모드 해석(complex modal analysis)을 후속 연구에서 필요할 것으로 보인다.

Fig. 8

Three points in fully open helicotrema

Fig. 9

Deformations of the basilar membrane

4. 결 론

이 연구에서는 유체-구조 연성을 고려한 와우의 직선 FE 모델을 이용하여 와우공 크기가 와우의 동특성에 미치는 영향을 살폈다. 와우의 동특성은 와우의 입력 임피던스 기준으로 평가하였다. 와우공의 크기 변화에 따른 입력 임피던스의 계산 결과는 와우공의 크기가 200 Hz 미만에서 와우의 입력 임피던스에 큰 영향을 미친다는 것을 보여주었다. 와우의 입력 임피던스에서 첫 번째 골짜기는 와우공의 크기가 작아짐에 따라 저주파 방향으로 선형적으로 움직였다. 그리고 골짜기 형성의 원인 파악을 위해 와우공의 완전 개방과 완전 폐쇄의 경우에 대해 동적 응답을 비교하였다. 골짜기 형성 주파수 위치에서 와우의 유체 압력 분포는 길이 방향 움직임으로 나타났고, BM의 변위와 움직임에서 위상 변화가 조금씩 다른 것을 확인했다. 하지만 와우의 입력 임피던스의 피크가 저주파 방향으로 움직이는 정확한 원인은 아직 파악하지 못 하여, 이 움직임들이 와우공의 크기에 따라 와우의 입력 임피던스를 어떻게 변화시키는지에 대해 세부 메커니즘을 추가로 연구해야 할 것으로 판단된다.

향후 연구에서는 유체-구조 연성을 고려한 복합 모드 해석을 이용하여 와우의 입력 임피던스의 특징에 대해 좀 더 세부적으로 연구할 계획이다.

Acknowledgments

이 연구는 한국연구재단의 지원을 받아 수행된 연구이며(NRF-2018R1A2B2005391), 이에 감사드립니다.

References

• Kinsler, L. E., Frey, A. R., Coppens, A. B. and Sanders, J. V., 1999, Fundamentals of Acoustics, 4th Edition, John Wiley & Sons, New York, USA.
• Lee, D. and Ahn, T.-S., 2015, Statistical Calibration of a Finite Element Model for Human Middle Ear, Journal of Mechanical Science and Technology, Vol. 29, No. 7, pp. 2803~2815. [https://doi.org/10.1007/s12206-015-0609-9]
• Ahn, T.-S., Baek, M.-J. and Lee, D., 2013, Experimental Measurement of Tympanic Membrane Response for Finite Element Model Validation of a Human Middle Ear, SpringerPlus, Vol. 2, No. 1, p. 527. [https://doi.org/10.1186/2193-1801-2-527]
• Lee, D. and Ahn, T.-S., 2008, Development of Expenrimental Dummy and Measurements of Head-related Transfer Functions(HRTF) for Averaged Korean Head Shape, Transactions of the Korean Society of Noise and Vibration Engineering, Vol. 18, No. 8, pp. 841~848. [https://doi.org/10.5050/KSNVN.2008.18.8.841]
• Puria, S. and Allen, J. B., 1991, A Parametric Study of Cochlear Input Impedance, Journal of the Acoustical Society of America Vol. 89, p. 287. [https://doi.org/10.1121/1.400675]
• Mountain, D. C., Hubbard, A. E., Ketten, D. R. and Trehey O’Malley, J., 2003, The Helicotrema: Measurments and Models, Biophysics of the Cochlea, pp. 393~399. [https://doi.org/10.1142/9789812704931_0053]
• Xu, L. F., Ta, N., Rao, Z. S. and Tian, J. B., 2014, Finite Element Model of Human Cochlea Considering of the Helicotrema Size, Applied Mechanics and Materials, Vol. 456, pp. 576~581. [https://doi.org/10.4028/www.scientific.net/AMM.456.576]
• Kang, S. J. and Lee, D. H., 2018, Fluid-structure Coupled Analysis of Cochlear Responses with Transverse Isotopic Basilar Membrane, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 1, pp. 14~22. [https://doi.org/10.5050/KSNVE.2018.28.1.014]
• Braun, K., Böhnke, F. and Stark, T., 2012, Three-dimensional Representation of the Human Cochlea Using Micro-computed Tomography Data: Presenting an Anatomical Model for Further Numerical Calculations, Acta Oto-laryngologica, Vol. 132, No. 6, pp. 603~613. [https://doi.org/10.3109/00016489.2011.653670]
• Nastran, M., 2010, Dynamic Analysis User’s Guide, NSC Software.
• Lee, D. and Kang, S.-J., 2020, An Investigation of Spiral Effects in the Dynamic Responses of the Human Cochlea Considering Fluid-structure Interactions, The Jounal of the Acoustical Society of America, Submitted for Publications.
• Emadi, G., Richter, C.-P. and Dallos, P., 2004, Stiffness of the Gerbil Basilar Membrane: Radial and Longitudinal Variations, Journal of Neurophysiology, Vol. 91, No. 1, pp. 474~488. [https://doi.org/10.1152/jn.00446.2003]
• Diependaal, R. J. and Viergever, M. A., 1989, Nonlinear and Active Two-dimensional Cochlear Models: Time-domain Solution, Journal of the Acoustical Society of America, Vol. 85, No. 2, pp. 803~812. [https://doi.org/10.1121/1.397553]
• Steele, C. R. and Zais, J. G., 1985, Effect of Coiling in a Cochlear Model, Journal of the Acoustical Society of America, Vol. 77, No. 5, pp. 1849~1852. [https://doi.org/10.1121/1.391935]
• Cai, H., Manoussaki, D. and Chadwick, R., 2005, Effects of Coiling on the Micromechanics of the Mammalian Cochlea, Journal of the Royal Society Interface, Vol. 2, No. 4, pp. 341~348. [https://doi.org/10.1098/rsif.2005.0049]
• Dallos, P., Popper, A. N. and Fay, R. R., 1996, The Cochlea, Springer, New York, USA. [https://doi.org/10.1007/978-1-4612-0757-3]
• Dallos, P., 1970, Low-frequency Auditory Characteristics: Species Dependence, Journal of the Acoustical Society of America, Vol. 48, pp. 489~499. [https://doi.org/10.1121/1.1912163]
• Gan R. Z., Reeves B. P. and Wang, X., 2007, Modeling of Sound Transmission from Ear Canal to Cochlea, Annals of Biomedical Engineering, Vol. 35, pp. 2180~2195. [https://doi.org/10.1007/s10439-007-9366-y]
• Wang, X., Wang, L., Zhou, J. and Hu, Y., 2014, Finite Element Modeling of Human Auditory Periphery Including a Feed-forward Amplification of the Cochlea, Computer Methods in Biomechanics and Biomedical Engineering, Vol. 17, No. 10, pp. 1096~1107. [https://doi.org/10.1080/10255842.2012.737458]
• Kim, N., Homma, K. and Puria, S., 2011, Inertial Bone Conduction: Symmetric and Anti-symmetric Components, JARO, Vol. 12, pp. 261~279. [https://doi.org/10.1007/s10162-011-0258-3]
• Helpard, L., Li, H., Rask-Andersen, H., Ladak, H. M. and Agrawal, S. K., 2020, Characterization of the Human Helicotrema: Implications for Cochlear Duct Length and Frequency Mapping, Journal of Otolaryngology – Head & Neck Surgery, Vol. 49, Article No. 2. [https://doi.org/10.1186/s40463-019-0398-8]