자동격자생성 알고리듬을 이용한 주름관을 갖는 배관계의 효율적 진동 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, an automatic mesh generation algorithm was developed for efficient finite shell element modeling of piping systems with bellows. For pre-processing of finite element analysis, a pipe geometry should be modeled using meshing software. However, the finite element meshing process requires time-consuming efforts for complicated piping systems such as bellows. Therefore, this study proposed an algorithm that can efficiently generate finite shell elements automatically. To generate the finite shell element model of the pipe, this algorithm only needs the information of the centerline of the pipe and the corresponding radius that is identical to the finite beam element. Additionally, effects of bellows on the dynamic characteristics of a curved pipe were discussed. The variation of the natural frequencies and dynamic stiffness of the piping system with respect to the change of the location, height and width of the bellows were investigated. The suggested automatic mesh algorithm is advantageous for the modeling of pipes having complex shapes such as bellows. Hence, it has the potential to be useful in designing optimal bellows in piping systems that require numerous finite element analysis calculations.
Keywords:
Finite Element Method, Bellows Pipe, Automatic Mesh Generation, Quadrilateral Shell Element, Natural Frequency, Dynamic Stiffness키워드:
유한요소법, 주름관, 자동격자생성, 일반사각형 셸 요소, 고유진동수, 동강성1. 서 론
배관 시스템은 냉장고나 에어컨 등 가전제품의 냉매 압축기나 승용차의 배기계 등 다양한 산업현장에서 적용되고 있다. 일반적으로 산업계에서 배관의 동적 거동을 해석할 때는 유한요소법(FEM)을 주로 사용한다(1~3). 일반적으로 사용되는 직선배관과는 달리, 배관 단면의 반지름이 변하는 경우에는 형상의 복잡성으로 인해 더욱 다양한 동적 거동을 보이게 된다. 이런 현상을 이용한 대표적인 예시가 주름관(bellows)이다. 승용차의 배기계에서 주로 사용되는 주름관은 진동소스(엔진)와 다른 배관 시스템사이의 유연한 연결을 담당하고 있다. 주름관은 엔진의 진동으로부터 배관 시스템의 진동과 소음을 차단해 주는 역할을 한다. Lee et al.(4)은 유한요소 해석과 실차 실험 간의 상관성을 확보하는 방법을 제시하였다. Kim(5)은 FEM을 이용하여 주름관의 형상에 따른 응력변화를 해석하였다.
이러한 주름관을 해석하는 데에는 FEM뿐만 아니라 등가 보를 이용하는 방법도 최근까지 사용이 되고 있다. 주름관 만을 해석하는 경우가 아닌 주름관이 포함된 전체 배관의 형상을 유한요소 해석하는 경우에, 작은 크기의 주름관을 복잡한 형상 그대로 세밀하게 모델링하는 것이 비효율적이기 때문이다. Jakubauskas et al.(6)은 Timoshenko의 보 이론을 바탕으로 주름관 이론모델을 개발하였다. Watanabe et al.(7)은 등가 보 이론을 이용하여 주름관의 이론 안정성 해석과 실험적 연구를 수행하였다. Hong et al.(8)은 등가 보 모델링 방법을 이용하여 주름관의 동특성을 예측하였다. Bae et al.(9)은 복소전단 탄성계수를 갖는 다층 감쇠 보에 대한 등가유한요소 모델을 제안하였다. 그리고 Won et al.(10)은 점탄성 코어를 갖는 3층 샌드위치 감쇠 보의 강제진동 해석을 위한 등가 보 요소 모델링 방법을 제시하였다. Gawande et al.(11)은 등가 보 이론을 바탕으로 한 수학 모델, 유한요소 해석 그리고 실험적 접근법을 이용하여 간단한 형상을 갖는 주름관의 동특성에 대해 연구하였다. 그러나 주름관를 포함한 임의의 배관 시스템의 동적특성을 예측하기 위해서는 등가 보를 이용한 해석 방법보다는 주름관의 형상을 실제로 모델링한 유한요소 해석을 이용하는 것이 적절하다.
이에 이 연구에서는 다양한 형상의 주름관을 갖는 배관계를 효율적으로 유한요소 해석하기 위한 셸(shell) 요소 자동격자생성 알고리듬을 개발하였다. 이 연구에서 제안하는 배관의 자동 격자생성방법은 반지름이 변하는 임의 형상의 배관에 대하여 자동격자 생성이 적용이 가능하다. 배관 단면의 중심 좌표들과 각각의 중심좌표에 대한 반지름정보만 주어지면 유한요소모델을 자동으로 생성할 수 있다. 따라서 제안된 알고리듬은 주름관과 같은 복잡한 형상의 배관을 모델링하고자 할 때 유용하게 사용할 수 있다. 이 논문에서는 제안된 자동격자생성 알고리듬을 주름관을 갖는 배관에 적용하였다. 그리고 제안된 자동격자생성 알고리듬을 이용해 주름관의 설계변수를 바꾸어가며 수 많은 해석을 효율적으로 수행할 수 있었다. 이 해석 결과들을 후처리하여 주름관의 설계변수에 대한 동특성을 관찰하였다.
2. 주름관 요소의 자동 격자생성 이론
주름관 요소는 배관의 축방향에 따라 단면적이 변하는 셸 요소로 이루어져 있다. 이 절에서는 배관의 중심좌표와 반지름정보를 이용하여, 복잡한 모델링작업을 거치지 않고도 배관의 유한요소 격자(FE mesh)를 생성할 수 있는 방법을 제시한다.
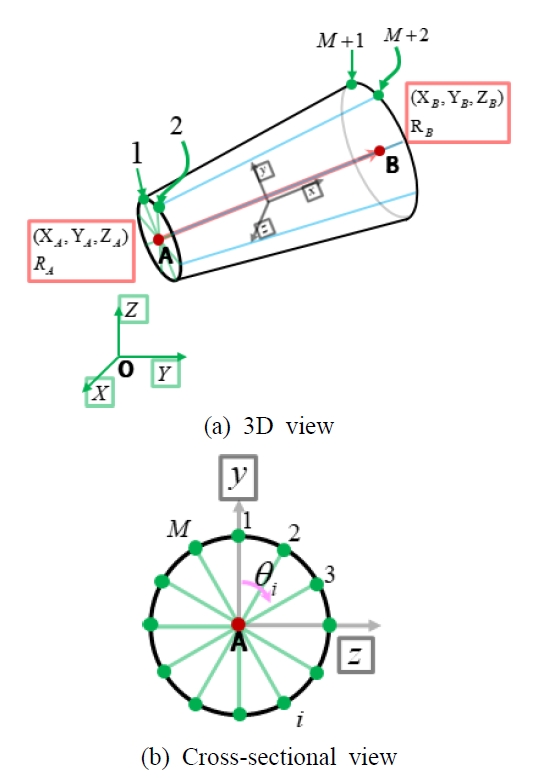
Fig. 1은 단위배관(unit pipe)의 옆면을 M개의 일반사각형 셸 요소(quadrilateral shell element)가 둘러싼 유한요소모델을 표현한 그림이다. 해당 모델은 2개의 중심점과 2M개의 절점과 M개의 요소로 이루어져 있다. 배관의 양 끝의 중심점을 각 A점 와 B점 라고 하자. 양 끝 단면의 중심좌표를 각각 (XA, YA, ZA)와 (XB, YB, ZB)라고 하고, 반지름은 RA와 RB라고 하자.
각 중심점 주위에는 M개의 절점이 존재하는데, 절점의 좌표는 다음과 같은 방법으로 얻을 수 있다. 먼저, Fig. 1의 (b)에서 단면 A 상에 존재하는 점 i번째 절점의 좌표를 (Xi, Yi, Zi)라고 하면, 위치 벡터는 식 (1)과 같이 표현할 수 있다.
| (1) |
다음으로, 배관의 진행방향을 x축으로 하고 중심을 점 A로 하는 국소 좌표계(local coordinate)에서 i번째 절점의 위치 벡터는 식 (2)와 같이 표현할 수 있다.
| (2) |
여기서, M은 배관를 원주방향으로 나누는 절점의 개수이다. 식 (1)과 식 (2)로부터 다음과 같은 관계식을 유도할 수 있다.
| (3) |
식 (3)을 행렬식으로 표현하면 다음과 같다.
| (4) |
여기서, [L3]은 변환 행렬이며, 변환 행렬의 각 요소는 국소 좌표계와 전체 좌표계(global coordinate)의 단위벡터 간의 내적 값이다.
따라서 단면 A 상에 존재하는 i번째 절점의 좌표 값은 식 (5)와 같다.
| (5) |
마찬가지로, 단면 B상에 존재하는 i번째 절점의 좌표 값은 식 (6)과 같다.
| (6) |
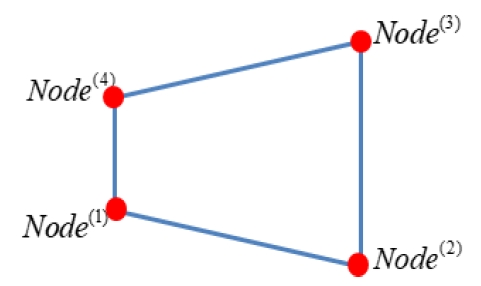
Fig. 1에 나타낸 유한요소모델에는 총 M개의 일반사각형 셸 요소(quadrilateral shell element)가 존재한다. 일반사각형 셸 요소는 Fig. 2와 같이 4개의 절점으로 구성되어있다. Fig. 1에 나타낸 유한요소모델의 각 요소를 구성하는 4개 절점의 번호는 Table 1과 같다.
이제 임의의 형상을 갖는 배관의 셸(shell) 유한요소모델 생성방법에 대하여 논의하고자 한다. 임의의 배관 유한요소모델은 Fig. 1에 나타낸 단위배관(unit pipe)의 유한요소모델이 연속적으로 연결된 것으로 생각할 수 있다.
Fig. 3은 임의의 곡선관(curved pipe)를 N개의 중심점에 대하여 (N-1)개의 단위배관의 연결로 표현한 그림이며, 이 연구에서 제안하는 자동격자 생성법의 입력 정보이다.
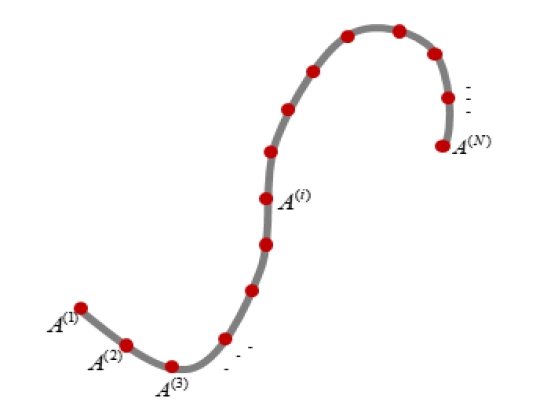
Centerline and center points of arbitrary pipe which is the input data for automatic mesh generation
Fig. 3에 나타낸 중심선 주위로 일반사각형 셸 요소를 둘러싸면, 임의의 배관에 대한 셸(shell) 요소로 이루어진 유한요소모델을 얻을 수 있다. 이 유한요소모델은 (M×N)개의 절점과 (M×(N-1))개의 요소를 갖는다. 각 절점의 좌표는 식 (2)나 식 (6)과 마찬가지로 N개의 중심점의 전체(global) 좌표와 해당 중심점에서의 배관의 반지름을 알면 구할 수 있다.
절점 번호는 중심점 A(i)주위에서 M(i-1)+1에서 Mi까지 차례로 부여된다. 요소 번호는 A(i)과 A(i+1)사이의 i번째 단위배관(unit pipe)의 주위에서 M(i-1)+1에서 Mi까지 차례로 부여된다.
각 요소를 구성하는 4개의 절점 번호는 다음과 같다. 여기서 e는 요소 번호이다.
| (7) |
3. 주름관의 영향
주름관의 설계변수로 4가지(산 폭, 골 폭, 산 높이, 주름관 삽입 위치)를 고려하였다. 그리고 제안한 자동격자 생성방법을 이용하여 자동으로 유한요소모델을 구성하고, 주름관의 설계변수에 대하여 전체 배관의 동특성이 어떻게 변하는지를 알아보고자 한다.
3.1 주름관의 형상에 따른 동특성 경향
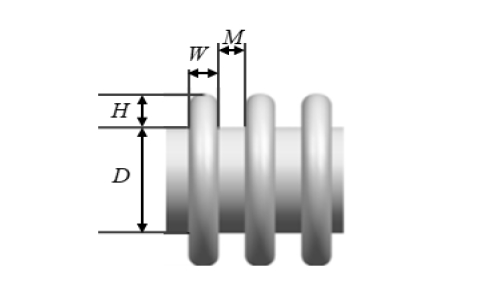
이 절에서는 주름관 설계변수들 중 주름관 자체의 형상에 관련된 설계변수 3가지(산 폭W, 골 폭M, 산 높이H)에 대하여, 주름관의 동특성이 어떻게 변하는지를 알아보고자 한다. Fig. 4는 주름관의 형상이다. 여기서 D는 배관의 직경이다.
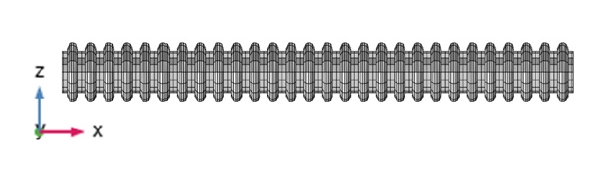
주름관의 형상에 대한 동특성을 알아보기 위한 해석 모델은 Fig. 5와 같다. 해당 배관 해석모델의 치수는 실제 가전제품에 사용되는 배관의 치수를 고려하여 선정하였다. 배관의 전체길이는 200 mm이고, 배관의 직경은 15.88 mm이고, 두께는 6 mm이다. 배관의 물성치는 Table 2에 나타내었다.
이 절에서는 Fig. 5와 같은 200 mm의 주름관에 형상설계변수 3가지(산 폭W, 골 폭M, 산 높이H)를 바꿔가며, 동특성(고유진동수 및 동강성)의 변화를 확인해 보고자한다.
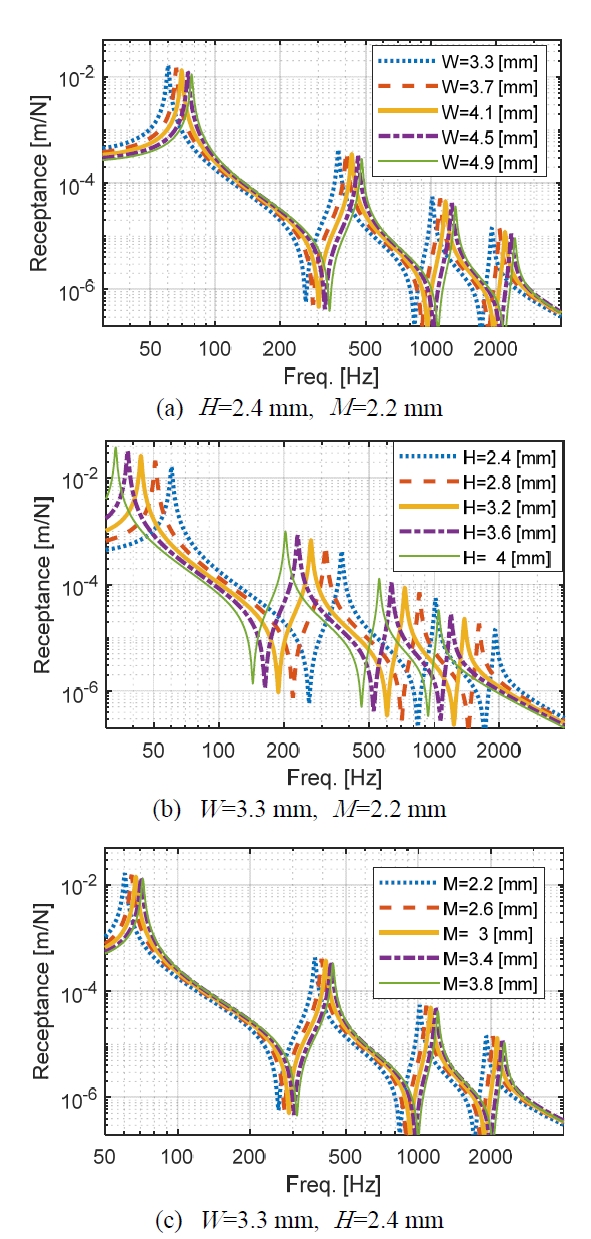
경계조건은 외팔보(clamped-free)이고, 배관의 자유단에 z방향으로 1 N의 조화가진(harmonic force)을 하였다. Fig. 6은 자유단에서의 자기 응답점의 receptance (변위/힘)의 크기를 그린 그래프이다. Fig. 6(a)는 산 폭W을 바꾸어가며 (H=2.4mm, M=2.2mm일 때) 그린 그래프이다.
Fig. 6(b)는 산 높이 H를 바꾸어가며(W=3.3mm, M=2.2mm일 때) 그린 그래프이고, Fig. 6(c)는 골 폭M을 바꾸어가며(W=3.3mm, H= 2.4mm일 때) 그래프이다.
Fig. 6의 그래프에서는 위와 같이 특정 설계변수에 따른 receptance의 변화를 관찰할 수 있다. Fig. 6의 (a), (b), (c)에서 각 설계변수는 점선, 파선, 굵은 실선, 일점쇄선, 얇은 실선 순으로 작아진다.
Fig. 6부터 각 주름관의 형상 설계변수에 대한 동특성의 변화를 관찰 할 수 있다. 동특성에서 중요한 지표들 중 2가지는 고유진동수와 동강성이다.
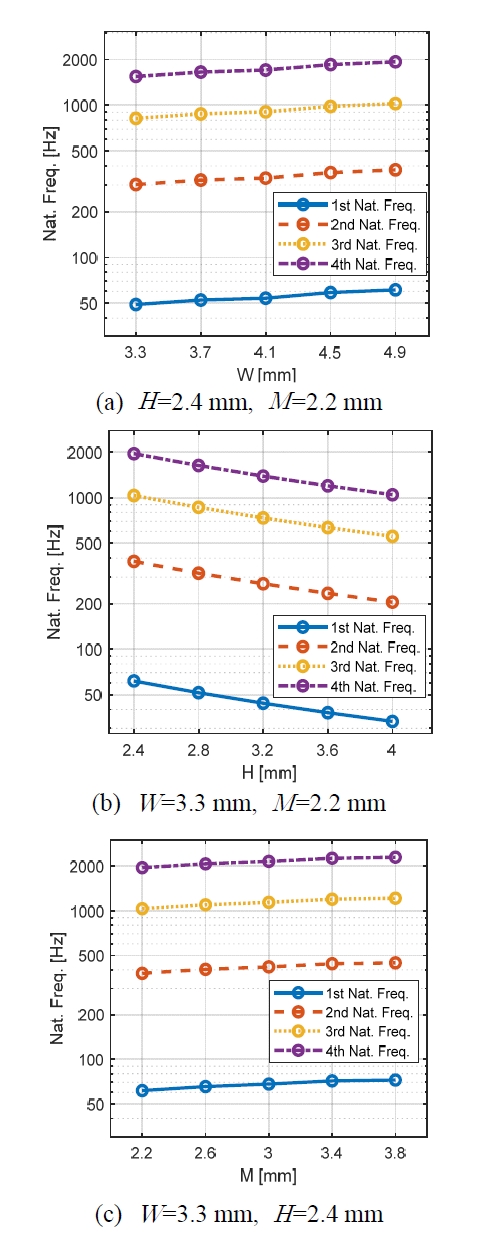
3가지 형상 설계변수에 대한 1차~4차 고유진동수의 변화를 Fig. 7에 나타내었다. Fig. 7에서 실선, 파선, 점선, 일점쇄선 그래프는 각각 1차, 2차, 3차, 4차 고유진동수를 의미한다. Fig. 7의 (a), (b), (c) 그래프에서는 각 각 산 폭W, 산 높이H, 골 폭M에 대한 1차~4차 고유진동수의 변화를 관찰할 수 있다.
Fig. 7을 관찰해보면, 산 폭W과 골 폭M이 증가할수록 1차~4차 고유진동수가 증가하는 것을 알 수 있다. 반대로, 산 높이H가 증가할수록 고유진동수는 감소하였다. 또한, Fig. 7의 세 가지 변수에 대한 그래프 중 산 높이H에 대한 고유진동수의 변화가 가장 민감한 것을 확인할 수 있다.
동강성(dynamic stiffness)은 receptance의 역수로 얻을 수 있고, 정강성(static stiffness)은 0 Hz일 때의 동강성의 값이다.
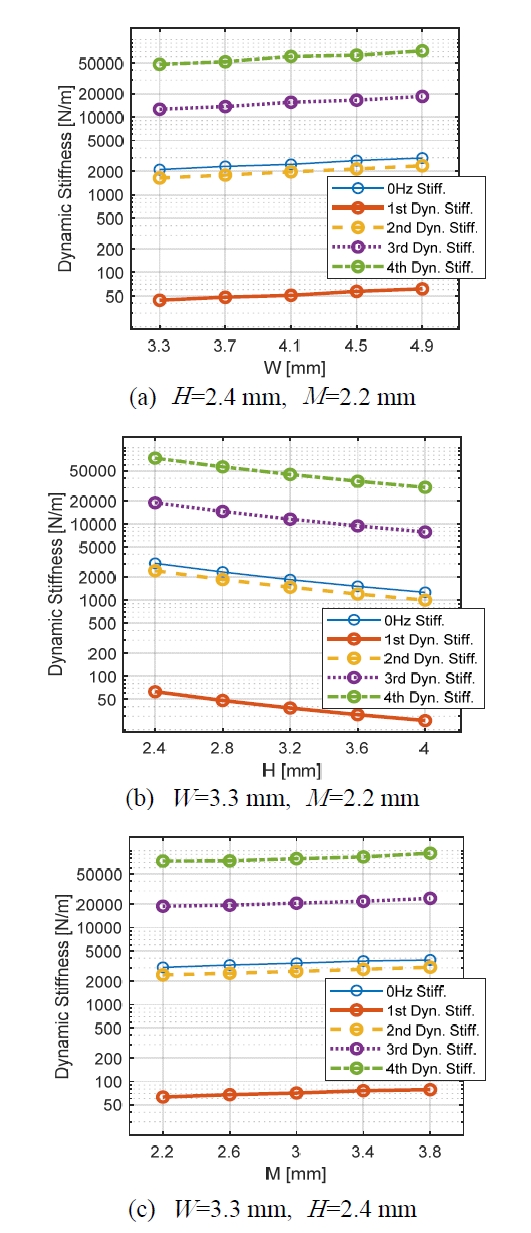
3가지 주름관 형상 설계변수에 대한 1차~4차 동강성과 정강성 (at 0 Hz)의 변화를 Fig. 8에 나타내었다. Fig. 8에서 얇은 실선, 굵은 실선, 파선, 점선, 일점쇄선 그래프는 각각 정강성, 1차, 2차, 3차, 4차 동강성을 의미한다. Fig. 8의 (a), (b), (c) 그래프에서는 각 각 산 폭W, 산 높이H, 골 폭M에 대한 정강성과 동강성의 변화를 관찰할 수 있다.
Fig. 8을 관찰해보면, 산 폭W과 골 폭M이 증가할수록 정강성과 1차~4차 동강성은 증가한다. 반대로, 산 높이H가 증가할수록 정강성과 동강성은 감소하였다. 또한, Fig. 8의 세 가지 변수에 대한 그래프 중 산 높이H에 대한 정강성과 동강성의 변화가 가장 민감한 것을 확인할 수 있다. 즉, 각 설계변수에 대한 동강성과 고유진동수의 경향이 유사한 것을 확인할 수 있었다.
3.2 주름관의 위치에 따른 동특성의 경향
이 절에서는 임의의 배관에서 주름관이 삽입되는 위치에 대하여, 주름관의 동특성이 어떻게 변하는지를 알아보고자 한다.
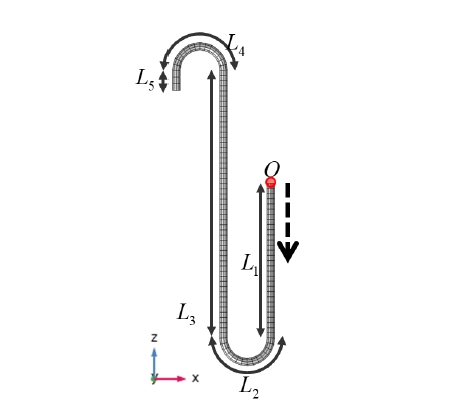
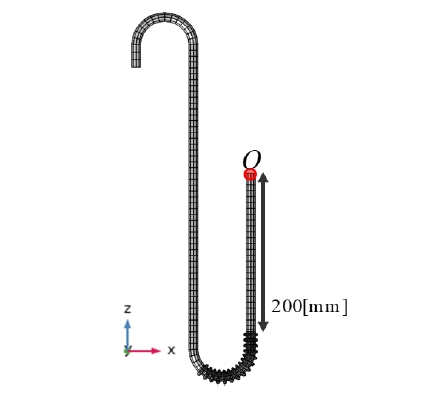
주름관의 삽입위치 Lst에 대한 동특성을 알아보기 위한 해석 모델은 Fig. 9와 같다. 여기서 점 O는 배관 진행방향의 시작지점이다.
해당 배관 해석모델의 치수는 실제 가전제품에 사용되는 배관의 치수를 고려하여 선정하였다. 배관의 전체길이는 863.2 mm이고, 배관의 직경 D는 11.7 mm이고, 두께는 1 mm이다. 배관의 각 파트의 길이는 L1=225.0 mm, L2=π×35 mm=110.0 mm, L3=389.1 mm, L4=π×35 mm=110.0 mm 그리고 L5=29.1 mm이다.
배관의 물성치는 Table 2에 나타내었다. Fig. 9에 삽입 될 주름관의 형상(geometry)은 W=4.1 mm, H=3.2 mm, M=3.0 mm 그리고 LBel=106.5 mm이다. 여기서 LBel은 주름관의 길이이다.
예를 들어 주름관이 점 O에서부터 떨어진 거리, 즉, 주름관의 삽입위치 Lst가 200 mm 일 때 배관의 형상은 Fig. 10과 같다.
이 절에서는 Fig. 9의 곡선관에 주름관의 삽입위치 Lst를 변화시켜가며, 동특성(고유진동수 및 동강성)의 변화를 확인해 보았다. 이를 파악을 위하여 주름관을 점 O에서부터 시작하여 10 mm씩 이동시켜가면서 75번의 유한요소 모델링과 유한요소해석을 수행하였다. 경계조건으로는 점 O을 6자유도 구속하고, 배관의 반대 끝단에 자유(free)경계조건으로 둔다. 배관의 자유단에 y방향으로 1N의 조화가진(harmonic force)을 하였다.
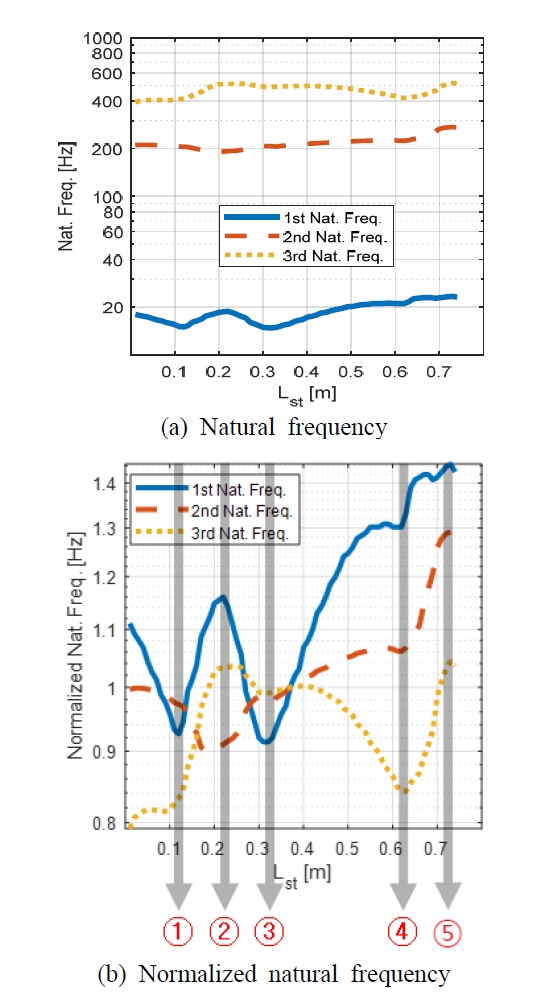
Fig. 11의 (a)는 주름관의 삽입위치 Lst에 따른 고유진동수 그래프이다. Fig. 11(b)는 Lst에 따른 고유진동수의 변화를 자세히 살펴보기 위해, Lst=370 mm 일 때의 1차~3차 고유진동수를 기준으로 정규화한 그래프이다. 각 그래프에서 실선, 파선, 점선 그래프는 각각 1번째, 2번째, 3번째 고유진동수를 의미한다. Fig. 11(b)의 ①은 주름관이 1번째 곡선배관부에 진입하는 지점으로, L1-LBel=118.5 mm이다. ②는 주름관이 완전히 1번째 곡선배관부분에 들어간 지점으로, L1=225.0 mm에서 L1+L2-LBel =228.5 mm사이이다. ③은 주름관이 1번째 곡선배관부에서 완전히 빠져나온 지점으로, L1+L2-LBel=335.0 mm이다. ④는 주름관이 2번째 곡선 배관부를 진입하는 지점으로, L1+L3+L3-LBel =617.6 mm이다. ⑤는 주름관이 완전히 2번째 곡선배관부에 들어간 지점으로, L1+L2+L3=724.1 mm에서L1+L2+L3+L4-LBel=727.6 mm사이의 구간이다.
Fig. 11를 보면 주름관의 삽입위치와 배관 커브구간의 상대적인 위치에 따라 기울기가 급격하게 바뀌는 지점이 발생하는데, 그 지점이 바로 ①~⑤지점이다.
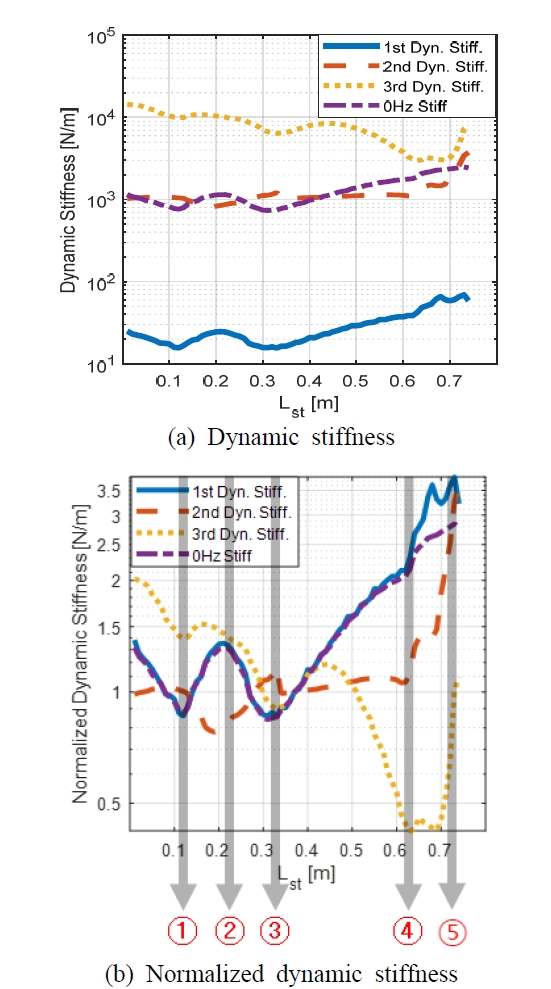
Fig. 12의 (a)는 주름관의 삽입위치 Lst에 따른 동강성과 정강성 (at 0 Hz) 그래프이다. 마찬가지로, Fig. 12의 (b)는 Lst에 따른 동강성의 변화를 자세히 살펴보기 위해, Lst=370 mm일 때의 동강성의 값을 기준으로 정규화한 그래프이다. 각 그래프에서 실선, 파선, 점선, 일점쇄선 그래프는 각각 1번째, 2번째, 3번째 동강성 그리고 정강성를 의미한다. Fig. 12(b)에 나타낸 ①~⑤ 구간의 의미는 Fig. 11(b)에서와 동일하다.
Fig. 12를 보면 ‘주름관의 삽입위치’와 ‘배관의 곡선부분’의 상대적인 위치에 따라, 동강성의 기울기가 급격하게 바뀌는 지점이 발생하는데, 그 지점은 ①~⑤지점이다. 이러한 특징은 고유진동수의 경향과 흡사하다.
Fig. 11과 Fig. 12를 보면, ‘주름관 삽입위치’에 따른 배관의 동특성은 ‘주름관이 전체 배관에서 차지하는 위치’에 따라, ‘주름관의 삽입위치’와 ‘배관의 곡선부분’의 상대적인 위치에 따라, ‘동특성(고유진동수와 동강성)의 차수’에 따라 달라지는 것으로 보인다. 즉, 삽입위치 Lst는 여타의 여타의 형상관련 설계변수(산 폭, 산 높이, 골 폭)와는 달리 임의의 배관의 형상에 따라 동특성이 달라지는 것을 알 수 있다. 따라서 주름관의 삽입위치 Lst에 따른 전체 배관 시스템의 동특성은 배관의 형상이 바뀔 때마다 바뀌기 때문에, 배관의 설계변경이 이루어질 때마다 매번 새로 파악해야 한다는 것을 알 수 있다.
4. 결 론
이 연구에서는 배관의 효율적 유한요소 모델링을 위한 자동격자생성 알고리듬을 개발하였다. 제안된 알고리듬은 보(beam) 유한요소모델과 같이 ‘배관 단면의 중심 좌표들’과 ‘각 중심좌표에 대한 반지름정보’만 알면 자동으로 유한요소모델을 만들어 준다는 특징이 있다. 이런 특징으로 인하여 이 연구에서 제시한 자동격자생성 알고리듬을 사용하면 효율적으로 복잡한 형상을 갖는 배관 시스템의 동특성을 파악하는 것이 가능하였다. 그리고 이 자동격자생성 알고리듬을 이용하여 주름관이 들어간 배관의 동특성을 효율적으로 분석할 수 있었다.
제안된 자동격자생성 알고리듬을 이용해 주름관의 설계변수 4가지(산 폭, 골 폭, 산 높이, 주름관 삽입위치)를 바꾸어가며 수많은 해석을 효율적으로 수행하였다. 이 해석 결과들을 후처리하여 주름관의 4가지 설계변수에 대한 동특성(고유진동수, 동강성)을 관찰하였다.
그 결과, 주름관 자체의 형상에 관련된 설계변수 3가지(산 폭, 골 폭, 산 높이)에 대한 동특성의 변화는 다음과 같았다. 먼저, 산 폭과 골 폭이 증가할수록 주름관의 고유진동수와 동강성이 증가하였다. 반대로, 산 높이는 증가할수록 주름관의 고유진동수와 동강성이 감소하였다. 또한, 산 높이의 변화에 대한 고유진동수와 동강성의 변화가 가장 민감하였다. 주름관의 삽입위치에 따른 배관의 동특성은 배관자체의 형상에 따라 크게 달라졌다. 따라서 주름관의 삽입위치에 따른 배관 시스템의 동특성은 배관의 설계변경이 이루어질 때마다 수많은 해석결과를 통해 새로 파악해야 한다는 것을 알 수 있었다.
Acknowledgments
이 논문은 부산대학교 기본연구지원사업(2년)에 의하여 연구되었음.
References
-
Lee, Y.-G., Jung, B.-K. and Jeong, W.-B., 2016, Optimization of the Shape of Loop-pipe in a Reciprocating Compressor Using Genetic Algorithm, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 4, pp. 398~405.
[https://doi.org/10.5050/KSNVE.2016.26.4.398]

-
Seo, Y.-S., Jeong, S.-H., Lee, S.-H., Hong, C.-S. and Jeong, W.-B., 2006, Vibration Analysis of Pipes Considering Fluid Pulsation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 10, pp. 1050~1056.
[https://doi.org/10.5050/KSNVN.2006.16.10.1050]

-
Lee, S.-H., Jeong, W.-B. and Seo, Y.-S., 2008, Finite Element Vibration Analysis of a Curved Pipe Conveying Fluid with Uniform Velocity, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 18, No. 10, pp. 1049~1056.
[https://doi.org/10.5050/KSNVN.2008.18.10.1049]

- Lee, J. B., Park, J. S., Shin, G. C., Nam, T. W. and Lee, J. O., 2002, Comparison of Stress Evaluation in vehicle of Automobile Exhaust System with Dynamic Stress Analysis, Proceedings of the KSNVE Annual Spring Conference, pp. 1275~1282.
-
Kim, J.-B., 2010, A Study on Structural Analysis for the Bellows of Automotive Exhaust System, Journal of Korea Academia-Industrial Cooperation Society, Vol. 11, No. 4, pp. 1192~1196.
[https://doi.org/10.5762/KAIS.2010.11.4.1192]

-
Jakubauskas, V. F. and Weaver, D. S., 1998, Transverse Vibrations of Bellows Expansion joints. Part II: Beam Model Development and Experimental Verification, Journal of Fluids and Structures, Vol. 12, No. 4, pp. 457~473.
[https://doi.org/10.1006/jfls.1997.0152]

-
Watanabe, M., Kobayashi, N. and Wada, Y., 2004, Dynamic Stability of Flexible Bellows Subjected to Periodic Internal Fluid Pressure Excitation, Journal of Pressure Vessel Technology, Vol. 126, No. 2, pp. 188~193.
[https://doi.org/10.1115/1.1687380]

-
Hong, J. H., Kim, Y. D., Lee, N. Y. and Lee, S. W., 2010, Prediction of Dynamics of Bellows in Exhaust System of Vehicle Using Equivalent Beam Modeling, Transactions of the Korean Society of Mechanical Engineers A, Vol. 39, No. 11, pp. 1105~1111.
[https://doi.org/10.3795/KSME-A.2015.39.11.1105]

-
Bae, S.-H., Won, S.-G., Jeong, W.-B., Cho, J.-R. and Bae, S.-R., 2011, Finite Element Vibration Analysis of Multi-layered Damped Sandwich Beam with Complex Shear Modulus, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 21, No. 1, pp. 9~17.
[https://doi.org/10.5050/KSNVE.2011.21.1.009]

-
Won, S. G., Bae, S. H., Cho, J. R., Bae, S. R. and Jeong, W. B., 2013, Three-layered Damped Beam Element for Forced Vibration Analysis of Symmetric Sandwich Structures with a Viscoelastic Core, Finite Elements in Analysis and Design, Vol. 68, pp. 39~51.
[https://doi.org/10.1016/j.finel.2013.01.004]

-
Gawande, S. H. and Pagar, N. D., 2018, A Combined Numerical and Experimental Investigation on the Effect of Dynamics Characteristics of Metal Expansion Bellows, Journal of Vibration Engineering & Technologies, Vol. 6, pp. 401~416.
[https://doi.org/10.1007/s42417-018-0053-0]


Man-Su Park received B.S. and M.S. from Pusan National University in 1997 and 1999, respectively. His major is rotor vibration. He is currently working at LG Electronics and leader of Air-solution CAE team.

Min-Jung Sim received B.S. and M.S. from Pusan National University in 2016 and 2018, respectively. She is currently a Ph. D candidate at Pusan National University. Her major is noise and vibration. Her research interests are in the area of finite/boundary element analysis of noise and vibration and multi-physics interactions.

Seong-gil Jang received B.S. and M.S. from Pusan National University in 2009 and 2011, respectively. His major is noise and vibration. He is currently working at LG Electronics and is researching the noise and vibration of air-conditioners.

Weui-Bong Jeong received B.S. and M.S. degrees from Seoul National University in 1978 and from KAIST in 1980, respectively. He then received his Ph.D. degree from Tokyo Institute of Technology in 1990. Dr. Jeong is currently a professor at the department of mechanical engineering at Pusan National University in Busan, Korea. His research interests are in the area of the measurement and signal processing, finite/boundary element analysis of noise and vibration, fluid-structure interactions and acoustics-structure interactions.