발전기 고정자 웨지 건전성평가를 위한 신호분석 기법
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper proposes the signal analysis technique for the evaluation of generator stator wedge tightness. To improve the existing qualitative method based on sound inspection, an impact excitation test was performed on the manufactured test bed similar to that of the domestic 500 MW generator. Six features were selected from the frequency and time domain through analysis of the vibration and force signals generated by the impact test. Moreover, a method to visually discriminate the status of wedge tightness based on 3D space is proposed.
Keywords:
Generator Stator Wedge, Wedge Tightness, Statistic Feature, Impact Test키워드:
발전기 고정자 웨지, 웨지 체결 강도, 통계적 특징값, 충격 가진 시험1. 서 론
발전기의 고정자(stator)에는 고정자 권선을 보호하고 지지하기 위해 웨지(wedge)를 활용하여 고정하고 있다. 웨지는 기계적 전자기적 하중이 결합된 영향으로 발생되는 고정자 코일(stator coil) 진동을 기계적으로 예방할 수 있는 유일한 부품으로 웨지가 삽입되어 있는 강도에 따라서 웨지의 조임 상태가 달라지며 이를 웨지 체결 강도(tightness)라 한다.
웨지의 체결강도가 느슨해지거나 결함이 발생되면 고정자 슬롯(stator slot)에 고정자 코일을 단단히 고정하지 못하고 고정밀 절연체의 열화 또는 고장으로 이어져 전자기력(electromagnetic force) 불균형에 따른 높은 수준의 진동을 발생시킨다. 이에 따라 국내 발전소에서는 발전기 고정자의 웨지 체결강도 저하와 열화현상으로 인한 절연파괴 사고 발생을 미연에 방지하기 위해 발전기 고정자 웨지 검사를 주기적으로 수행하고 있다. 발전기 예방점검 시 주요 관심사 중 하나가 고정자 코일의 정상상태 유무이며, 고정자의 무결성을 정량적으로 평가하기 위해 수행되는 검사 중 하나가 고정자 웨지의 체결강도검사이다. 현재 웨지의 체결강도를 검사하는 방법은 전문 검사 인력이 수동으로 웨지를 타격 후 음향을 듣고 체결 강도를 판단하는 타음에 의한 청음 검사 방식이다. 현행과 같이 사람이 직접 웨지를 타격하여 검사하는 진단 방식은 작업자의 숙련도 및 주관적 경험과 같은 정성적인 요인에 따라 진단 결과가 상이해질 수 있으므로 웨지의 체결강도를 정량적으로 판단할 수 없는 문제가 발생할 수 있다.
이 연구에서는 현장에서 수행되고 있는 정성적인 검사방법을 개선하기 위해 임팩트 해머와 가속도 센서를 이용하여 웨지를 타격하는 임팩트 시험을 수행하였으며 타격 시 발생 된 진동가속도(acceleration)와 힘(force)에 대한 신호 특성을 분석해 주파수 영역과 시간 영역에서 웨지의 체결 상태를 잘 반영하는 통계적인 특징(feature)값을 추출하였다. 이를 통해 기존의 타음 검사방법을 벗어나 데이터에 기반을 둔 정량적인 검사방법을 제안하고자 한다.
2. 데이터 측정 및 신호 분석
2.1 데이터 측정
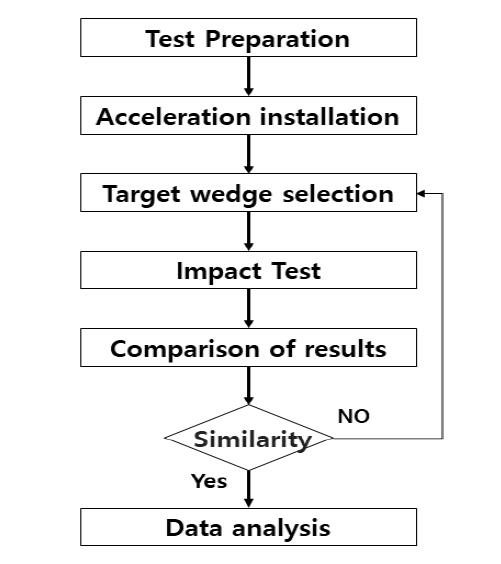
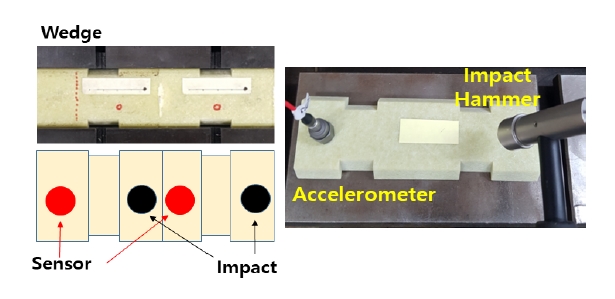
웨지 체결강도를 시험하기 위해 국내 500 MW 발전기와 동일한 사양의 시험 장치를 제작하고 웨지의 상태를 모사하기 위해 이상(느슨한 체결)과 정상(강한 체결)으로 구분하여 제작하였다. Fig. 1의 ①∼②번은 정상웨지이며, ③∼④번은 웨지의 체결강도가 느슨한 이상웨지이다. 시험은 Fig. 2의 절차에 따라 수행하였다.
사용된 계측기는 OROS 8.3 model을 사용하였으며, 진동 가속도계 센서의 감도는 10.2 mV/m/s2, 측정범위 10 kHz인 ICP 타입이고, 임팩트 해머의 감도는 22.5 mV/N, 측정범위는 4448 N이다. Fig. 3과 같이, 웨지의 좌측에 가속도 센서를 설치하고 임펙트 해머 타격 시 저주파수 노이즈로 인해 응답신호에 bias가 발생하지 않도록 타격지점을 조정하여 센서와 타격점의 설치 위치를 최적화하였다.
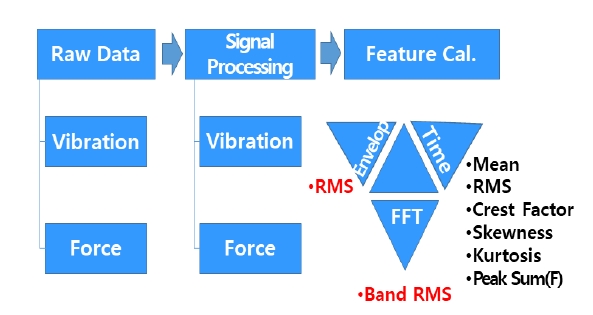
측정되는 대상 웨지의 체결강도에 따라 ○, △, X로 분류하며, 진동 가속도(acceleration) 및 힘(force) 신호를 계측하여 Fig. 4와 같이 특징값을 추출하였다. 특징값은 주파수 및 시간영역에 대한 통계값을 사용하였으며, 이 연구에서는 계측된 웨지 신호로부터 체결 상태를 잘 반영할 수 있는 특징값을 추가적으로 추출하였다.
2.2 신호분석
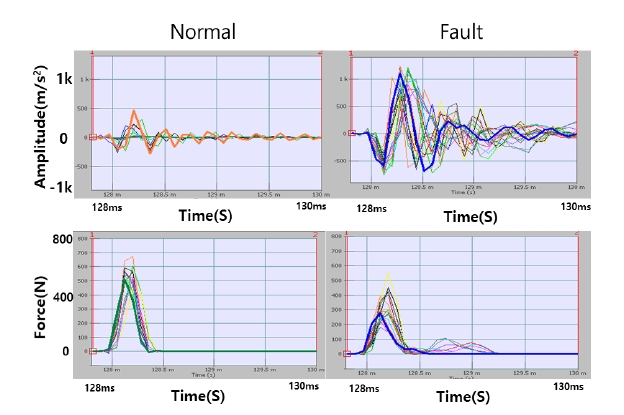
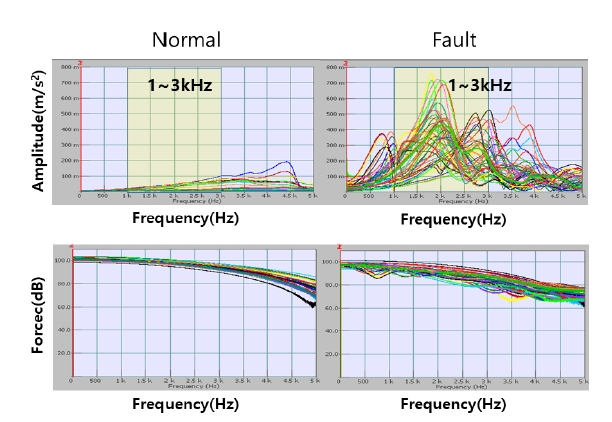
Fig. 5에서 알 수 있듯이, 시간에 따른 진동가속도(acceleration)와 힘(force)의 크기는 체결강도에 따라 반비례하는 것을 알 수 있다. 체결상태가 느슨해질수록 진동 가속도(acceleration)의 경우는 진폭크기가 높아지는 것을 알 수 있고, 힘(force)은 점차 크기가 낮아지는 것을 알 수 있다. 이는 체결강도가 높은 웨지의 경우 임팩트 충격이 가해지더라도 응답신호는 빠르게 감쇠하여 웨지로 전달되는 진동 가속도의 진폭 크기가 작은 것을 알 수 있다. 이에 반해 힘(force)은 체결강도가 높은 웨지에서 신호형태가 뾰족하고 상대적으로 크기가 큰 신호가 계측되고, 체결상태가 느슨해질수록 임펙트 크기는 낮고 점차 왜곡되는 것을 확인할 수 있다. 주파수 영역에 대해서는 Fig. 6과 같이 체결강도가 높은 경우 주파수의 진폭이 낮고 고주파 성분에서도 높지 않은 진폭이 형성된다. 반면 체결상태가 느슨해질수록 1 kHz ~ 3 kHz 영역의 주파수 영역에 점차 진폭이 높아지는 경향을 보이고 있다.
Fig. 5의 힘과 진동 가속도의 관계가 반비례한 것은 체결강도가 강할수록 Fig. 6 그래프 좌측의 높은 주파수 영역까지 가진하게 되므로 Fig. 5 그래프 좌측의 시간영역에서는 힘(force) 신호가 뾰족한 형상으로 나타난다. 체결강도가 느슨하면 Fig. 6의 우측과 같이 높은 주파수 영역까지 가진 하지 못해 Fig. 5의 우측과 같이 뭉툭한 형상이 나타난다. 이에 반해, 진동 가속도는 웨지가 느슨할수록 주변 지지물과 강하게 체결(부착)되어 있지 않아 작은 가진력에도 진폭이 커지는 것을 확인할 수 있다.
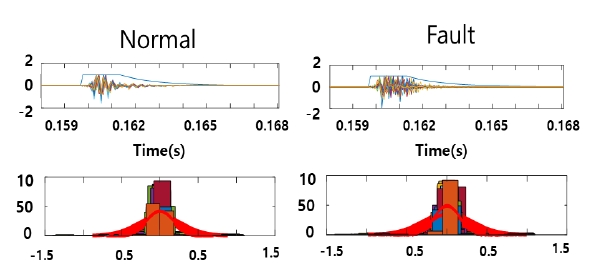
가속도(acceleration) 신호는 Fig. 7 상단의 그래프와 같이 매우 짧은 시간에 감쇠되는 특징이 있으며, FFT 분석 시에는 타격시에 발생되는 저주파수의 영향이 높아 웨지의 상태를 반영하는 고유주파수 추출이 어렵다.
이에 따라, 진동 가속도 진폭의 최대값으로 나누어 정규화(normalization)를 수행한 후 가중치를 부여한 함수를 원신호에 곱하여 센서로 들어오는 저주파의 잡음 및 bias를 제거하고 빠르게 감쇠되지 않는 신호를 제거함으로써 신호특성을 추출하기 위한 전처리를 수행하였다.
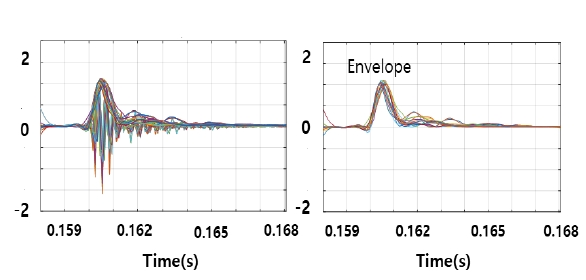
Fig. 8에서 좌측 그래프의 가속도(acceleration) 신호로부터 우측 그래프 같이 포락선(envelope) 성분을 추출하고 추출된 Envelope 신호를 FFT 변환하여 웨지의 특성주파수를 추출한다.
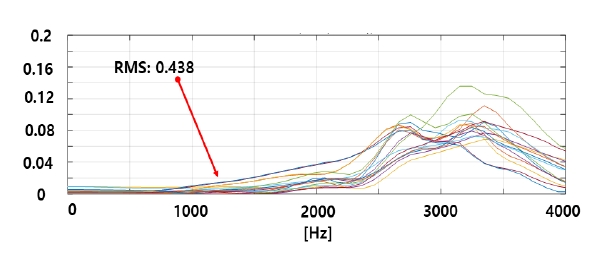
포락선(Envelope) 신호의 FFT 결과로부터 각 주파수의 크기를 제곱하여 Fig. 9와 같이 파워 스펙트럼으로 변환하였으며, 이는 작은 값과 큰 값의 크기차를 더 강화시킴으로써 특정 주파수 대역의 성분값의 특성을 잘 나타나게 한다. 이에 따라, 각 신호 별 파워 스펙트럼의 RMS를 특징값으로 사용하였다.
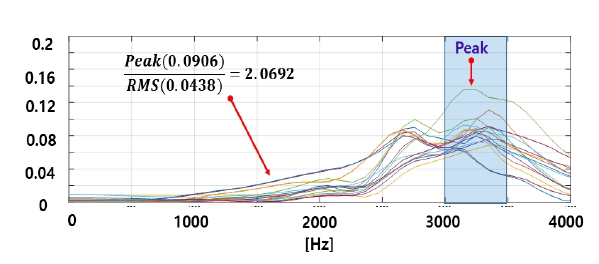
신호처리과정 후에 변환된 파워 스펙트럼을 이용해 Fig. 10과 같이 주파수의 최대 진폭(peak)값을 해당 신호의 실효치(root mean square, RMS)으로 나누어 특징값을 추출하였다. 주파수 영역에서 RMS는 각 진폭을 합산하게 되면 RMS를 구할 수 있다. 최대 진폭(peak)은 0 kHz ~ 4 kHz 범위에서 발생된 가장 큰 진폭값을 사용하였다. 이는 웨지의 상태(강한 결합 또는 느슨한 결합)에 따라 특성 주파수의 위치와 크기가 달라지는 것에 착안하여 해당 신호의 에너지값으로 최대 진폭(peak) 주파수를 나누어줌으로써 특성주파수의 상대적 크기값을 특징으로 사용하였다.
체결강도가 높은 웨지는 대체로 진폭이 Fig. 6 그래프 좌측과 같이 작아 실효치(RMS)도 낮고 최대 진폭(peak)값도 작다. 체결강도가 느슨한 웨지는 진폭이 상대적으로 높고 실효치(RMS)도 크게 나오며 최대 진폭값(peak)도 높게 나타난다. 특성 주파가 넓은 범위(1 kHz ~ 3 kHz)에 걸쳐 나타나는 경향이 있어실효치(RMS) 대비 최대 진폭(Peka)의 비를 특징점으로 사용하였다.
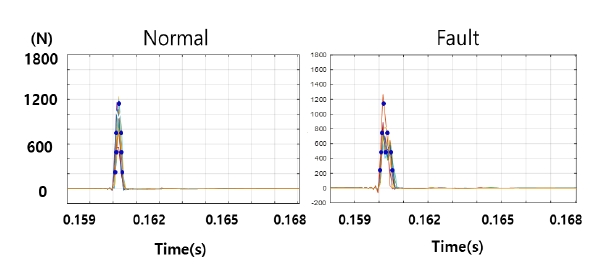
힘(force) 신호는 웨지의 체결 정도(강한체결, 느슨한 체결)에 따라 대상 웨지에 전달되는 힘의 크기가 달라진다. 체결강도가 높은 웨지는 타격된 힘의 크기가 잘 전달되므로 임펙트해머로 계측된 신호는 Fig. 11의 좌측과 같이 뾰족한 형태의 신호특성을 가지지만 체결강도가 느슨한 웨지는 힘전달이 되지 못해 신호가 뭉퉁해지거나 왜곡되는 특성을 가진다.
가진된 힘(force)의 특성을 이용해 힘(force) 신호의 각 충격량 값들을 합산하여 이를 특징값으로 사용하였다. 신호가 왜곡되거나 뭉퉁해 질수록 동일위치에서 충격량 값들이 더 많이 발생되므로 체결강도가 느슨한 이상웨지에서 충격량 값들의 합의 크기가 커진다.
3. 특징값 추출
계산된 특징점에 기반하여 웨지의 체결강도 검출을 시도하였으며, 특징값에 따라 정상과 이상과의 크기값이 차이가 클수록 좋은 특징값이라고 할 수 있다. 사용된 각 특징값과 이에 대한 각 정의는 Table 2에 요약 정리하였다.
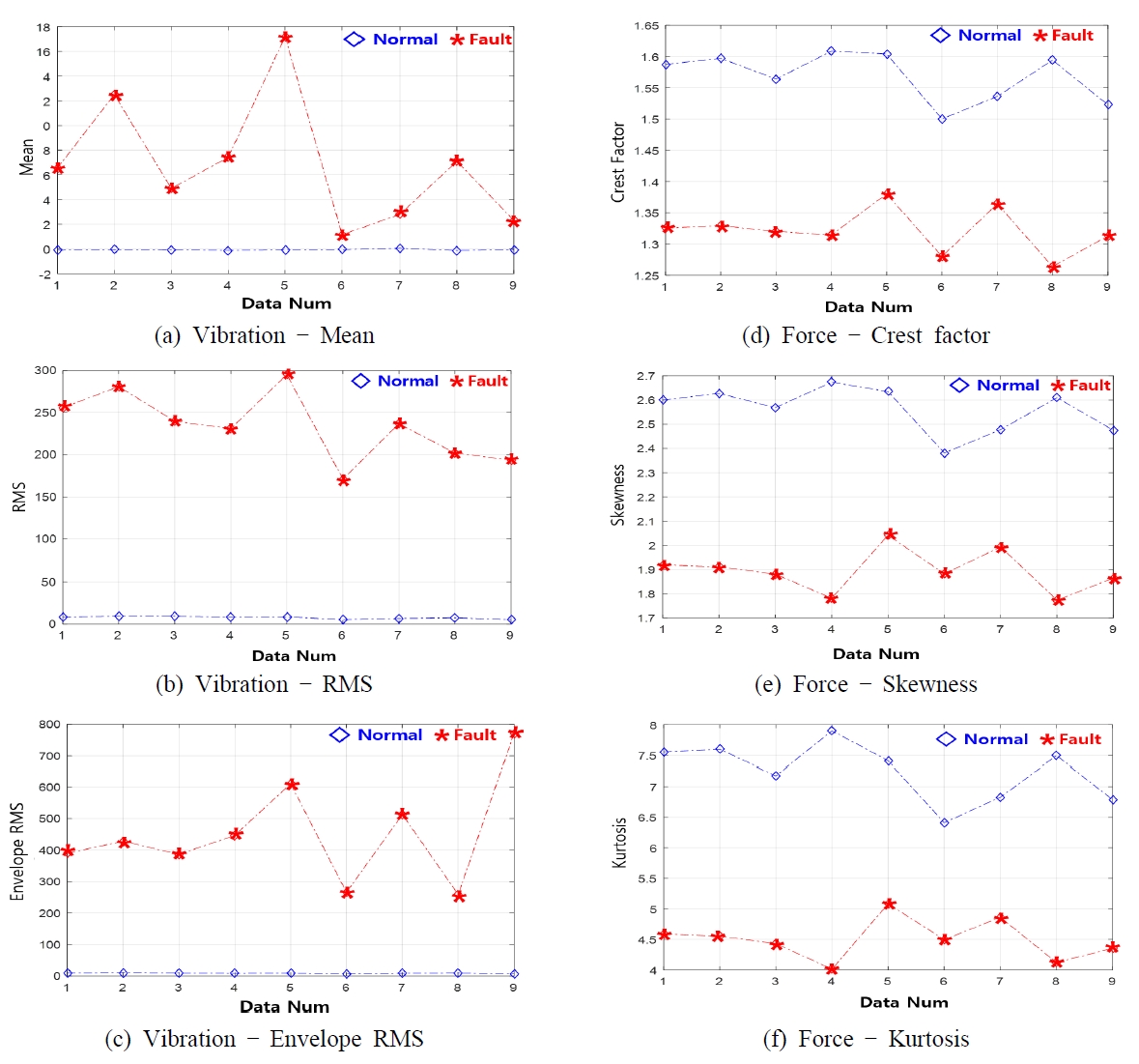
체결강도가 강하게 조여진 웨지와 느슨하게 조여진 웨지에 대해 8개의 특징점을 계산하여 진동 가속도(acceleration)와 힘(force)에 대해 각각 분별력이 높은 특징점을 아래 Fig. 12의 그래프로 나타내었다. 그래프의 결과와 같이 정상과 이상의 간격이 클수록 검출 변별력이 높은 특징값이다.
진동 가속도 신호는 8개의 특징값 중 평균(mean), 실효치(RMS), 포락선 실효치(envelope RMS)의 특징값이 웨지의 체결 상태를 구분하는 것으로 확인되었다. 힘(force) 신호는 파고율(crest factor), 왜도(skewness), 첨도(kurtosis)의 3가지 특징값이 웨지의 체결 상태를 구분하는 것으로 확인되었으며, 이에 대해 Table 3에 결과를 요약하였다.
결과를 살펴보면, 진동 가속도로부터 추출된 특징값은 앞서 설명한 진폭의 크기(magnitude)에 영향을 많이 받는 평균, 실효치가 분별력이 높은 것으로 나타났으며, 힘(force)으로부터 추출된 특징값은 신호의 형상(shape) 즉 뭉퉁하거나 왜곡된 정도를 표현할 수 있는 특징값이 분별력이 높게 나타났다.
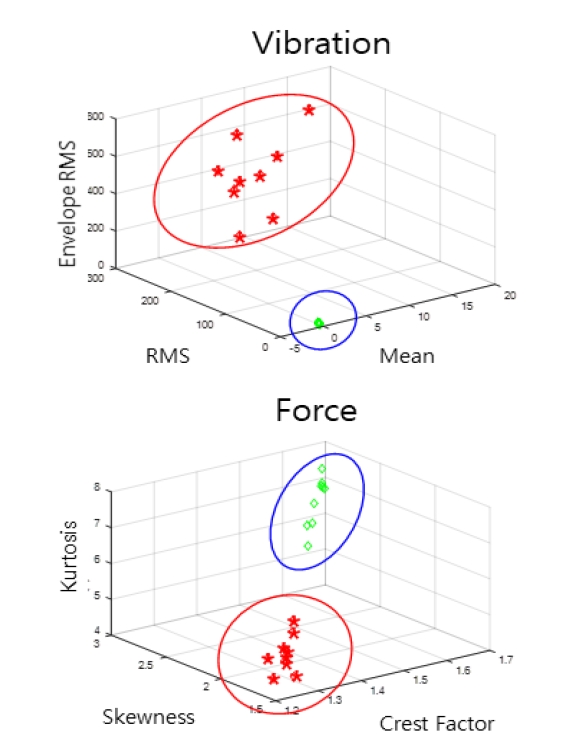
추출된 6개의 특징값을 3차원의 특징공간으로 각각 나타내본 결과 Fig. 13과 같이 정상(강한 체결강도)과 이상(느슨한 체결강도)이 가시적으로 분리가 되는 것을 확인할 수 있으며, 특징값을 이용한 웨지의 체결 상태를 판단하는데 효율적인 시각화 방법임을 확인하였다.
4. 결 론
이 연구는 발전자 고정자 웨지 건전성평가를 위한 신호분석 기법에 관한 것으로 힘, 가속도 신호에 대한 특징점과 그의 결합을 제안하여 웨지의 체결 강도 측정의 정확성을 향상시킨다. 발전기 웨지의 체결강도를 확인하기 위해 진동 가속도 신호와 힘신호의 특징값을 이용하였으며, 진동 가속도는 평균(mean), 실효치(RMS), 포락선 실효치(envelope RMS)가 웨지의 체결 강도에 대한 변별력이 높았으며, 힘은 파고율(crest factor), 왜도(skewness), 첨도(kurtosis)가 변별력이 높은 것을 확인하였다. 추출된 특징점을 3차원 특징공간을 활용함으로써 웨지의 체결 상태를 시각적으로 판단할 수 있었다.
또한 다차원의 데이터를 활용함으로써 기존에 제안된 단차원 데이터에 기반한 방법론에 비해 오검출 가능성의 축소를 기대할 뿐 아니라 향후 자동화를 통해 정량화된 검사를 진행하여 반복성 있는 검사 및 진단 결과를 도출할 수 있으며, 전문가의 수동 진단을 대체하는 것이 가능할 것으로 예상된다. 최근 각광받고 있는 머신러닝 기법을 적용하여 이 연구에서 추출된 특징값을 이용 시 분류기(classifier)를 통해 측정결과의 신뢰도를 한층 더 높일 수 있을 것으로 기대된다.
기 호 설 명
| x : | 데이터의 평균 |
| xi : | 표본집단의 데이터 |
| xp : | 데이터의 최대진폭(peak) |
| xs : | 데이터의 실효치(RMS) |
| σ : | 표준편차 |
Acknowledgments
이 연구는 한국전력공사 전력연구원의 “Intelligent Digital Power Plant 구축(세부 1과제)” 연구과제의 지원으로 수행되었습니다.
References
-
Peng, X., Jia, Z., Gao, S., Guan, Z., Wang, L. and Wang, T., 2008, A New Method for Stator Slot Wedge Testingof Large Generators, IEEE Transactions on Dielectrics and Electrical Insulation, Vol. 15, No. 4, pp. 933~940.
[https://doi.org/10.1109/TDEI.2008.4591213]

-
Peng, X., Jia, Z., Gao, S., Wang, L., Guan, Z., Yang, J. and Wang, T., 2009, Laboratory Studies of a New Stator Slot Wedge Tester for HV Generators, IEEE Transactions on Energy Conversion, Vol. 24, No. 1, pp. 146~152.
[https://doi.org/10.1109/TEC.2008.2008881]

- Ma, X., Lu, W. and Xie, H., 2001, Detecting Loose Stator Wedges in Large Motors, Proceedings of 2001 International Symposium on Electrical Insulating Materials (ISEIM 2001), 2001 Asian Conference on Electrical Insulating Diagnosis (ACEID 2001), 33rd Symposium on Electrical and Ele, pp. 685~688.
-
Poombansao, T., Kongprawechnon, W., Theeraworn, C. and Kittipiyakul, S., 2015, Automatic Wedge Tightness Classifying System by Support Vector Machine, 2015 6th International Conference of Information and Communication Technology for Embedded Systems, pp. 1~5.
[https://doi.org/10.1109/ICTEmSys.2015.7110810]

- Poombansao, T., Kongprawechnon, W., Kittipiyakul, S., Theeraworn, C. and Charoenlarp, M., 2014, Automatic Classifying Method for Wedge Tightness by Support Vector Machine and Artificial Neural Network, The 6th International Conference on Soft Computing and Intelligent Systems, and The 13th International Symposium on Advanced Intelligence Systems.
-
Widodo, A. and Yang, B.-S., 2007, Application of Nonlinear Feature Extraction and Support Vector Machines for Fault Diagnosis of Induction Motors, Expert Systems with Applications, Vol. 33, No. 1, pp. 241~250.
[https://doi.org/10.1016/j.eswa.2006.04.020]

-
Widodo, A., Yang, B.-S. and Han, T., 2007, Combination of Independent Component Analysis and Support Vector Machine for Intelligent Faults Diagnosis of Induction Motors, Expert Systems with Applications, Vol. 32, No. 2, pp. 299~312.
[https://doi.org/10.1016/j.eswa.2005.11.031]

-
Widodo, A., Kim, E. Y., Son, J.-D., Yang, B.-S., Tan, A. C. C., Gu, D.-S., Choi, B.-K. and Mathew, J., 2009, Fault Diagnosis of Low Speed Bearing based on Relevance Vector Machine and Support Vector Machine, Expert Systems with Applications, Vol. 36, No. 3, Part 2, pp. 7252~7261.
[https://doi.org/10.1016/j.eswa.2008.09.033]

-
Hwang, W.-W. and Yang, B.-S., 2004, Fault Diagnosis of Rotating Machinery Using Multi-class Support Vector Machines, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 14, No. 12, pp. 1233~1240.
[https://doi.org/10.5050/KSNVN.2004.14.12.1233]

-
Son, J.-D., Niu, G., Yang, B.-S., Hwang, D.-H. and Kang, D.-S., 2009, Development of Smart Sensors System for Machine Fault Diagnosis, Expert Systems with Applications, Vol. 36, No. 9, pp. 11981~11991.
[https://doi.org/10.1016/j.eswa.2009.03.069]


Yong-Chae Bae received his Ph.D. degrees in Mechanical Engineering from Chonnam National University, Gwangju, Korea in 1995. Since 1986, he has been working for the Korea Electric Power Corporation Research Institute. He is currently a chief researcher with the Power Generation Lab., KEPCO Research Institute, Daejeon. His research interests include vibration analysis, mechanical integrity of generator stator windings, and monitoring and diagnostics of main equipment in power plants.

Joon-Seok Oh received his Master. degrees in Mechanical Engineering from Pukyong National University, Busan, Korea in 2011. Since 2019, he has been working for the Korea Electric Power Corporation Research Institute. He is currently a researcher with the Power Generation Lab., KEPCO Research Institute, Daejeon. His research interests include vibration analysis, signal processing, monitoring and diagnostics of main equipment in power plants.