수중날개 부가탄성을 고려한 고유 응답 예측 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
Analyses of natural behaviors of flexible underwater structures are necessary for designing flexible hydrofoils and propellers. The added mass and stiffness of hydrofoils and propellers have an influence on the natural frequencies of underwater structures. In the previous studies, only added mass was considered for the analysis. This resulted in an increase in the error of estimations of natural frequency at high speed conditions. Therefore, to predict the natural frequency variance of underwater structures, the added stiffness must be taken into account. In this paper, the added stiffness of underwater hydrofoils dependent on the flow speed is derived. The added stiffness is obtained from a change of the hydrodynamic force with structural displacement and is calculated for varying flow speeds. Hybrid FSI analyses of hydrofoils are performed by considering the added stiffness in the structural system of the FSI. The natural frequencies of the hydrofoil are compared with the experimental values. The results show that the flow speed–dependent added stiffness is required to accurately predict natural responses of underwater structures in high speed environment.
Keywords:
Added Stiffness, Hydrofoil, Natural Vibration, FSI키워드:
부가탄성, 수중날개, 고유 응답, 유체-구조연성1. 서 론
탄소강화섬유와 유리강화섬유와 같은 유연재료 제작 기술이 증가하며 강철로 제작하던 선박 및 해양구조물에 유연재료를 적용하는 사례가 증가하고 있다. 현재 소형 레저용 보트 및 어선 선체에 유연재료가 활발히 사용되고 있으며 수중날개와 추진기에 적용하기 위해 수중 구조에 대한 연구개발이 확대되고 있다. 유연체 구조는 주변 유체로부터 하중을 받았을 때 대변형이 일어나는 특징이 있다. 이런 유연체 특성을 이용하여 구조설계를 하면 저진동, 경량, 저소음, 저비용의 구조를 제작할 수 있다.
유연체 수중 구조를 설계하기 위해서 구조가 주변 유체로부터 유체동력학적 힘을 받았을 때 거동을 예측할 수 있어야 한다. 구조의 대변형이 일어나는 상황에서는 구조변위와 유체흐름이 서로 연성되는 현상이 발생한다(1,2). 이를 유체-구조연성이라 하며 해당 효과를 반영한 것이 유체-구조연성(fluid structure interaction, FSI) 해석이다. 유체-구조연성 해석은 공역학과 수력학 분야에 활발히 적용되고 있다. 공역학 분야의 경우 풍력발전기 날개, 공기터빈에 주로 적용되며(1,3~5), 수력학의 경우 수중날개와 추진기가 주요 대상이다(2,5,6). 유체-구조연성이 발생하는 환경에서는 구조가 주변 유체에 의한 부가효과를 받게 된다. 구조에 작용하는 부가효과에는 부가질량(added mass)과 부가탄성(added stiffness)이 있다(7,8). 수중 구조의 경우 공기중 구조보다 부가효과에 의한 영향이 더 크다. 이는 물의 밀도가 공기대비 103오더로 유체밀도와 구조밀도 사이 비율이 물에서 더 높기 때문이다. 따라서 풍력발전기 날개와 공기터빈에 대한 유체-구조연성 해석 시 부가효과를 무시하고 해석을 수행한다(1,3~5). 하지만 수중 구조의 경우 물의 특성에 따라 부가효과가 구조에 미치는 영향이 크다. 수중 구조물에 작용하는 부가효과 중 부가질량에 대한 연구는 활발히 진행되어 왔다. Zarruk et al.(9)은 날개형상에 대하여 임펄스(impulse) 응답 실험을 수행하여 수중과 공기중 고유주파수를 계측하고 부가질량에 의한 차이가 발생함을 보였다. Liang et al.(7)과 Liao et al.(10), Zeng et al.(11)은 음향-구조연성 기법을 이용하여 수중 구조에 작용하는 부가질량을 도출하였다. 실험결과와 해석결과를 비교하였으며, 음향-구조연성 기법을 이용하며 수중구조의 부가질량을 예측할 수 있음을 확인하였다. Chae et al.(12)은 공역학에서 제시된 Theodorsen 이론을 이용하여 수중날개 응답을 2차원으로 단순화 한 후 고유주파수를 도출하였다. 구조응답 해석과 실험을 비교한 결과 수중날개의 고유 응답을 단순화 모델로 예측할 수 있음을 확인하였다. Lee et al.(6)과 Li et al.(13)은 수중 추진기에 대하여 포텐셜 방법을 적용하여 부가질량을 고려하였다.
부가질량 예측 방법에 대한 검증은 모두 구조가 수중에 정지해 있는 상황에서 이루어졌다. 음향-구조연성 방법과 패널 방법, 구조거동 단순화 모델 모두 구조의 움직임이 없는 상황에 대해서 고유주파수를 정확하게 예측할 수 있다. 하지만 유동이 있는 상황에서는 수중 구조의 고유주파수가 변하는 현상이 나타나는 것이 실험을 통해 확인되었다(14~16). 유속이 빨라질수록 정지상태의 고유주파수와 비교했을 때 차이가 커지는 것을 알 수 있다. Seeley et al.(14)은 수중날개에 대해서 유속에 따른 수중 고유주파수를 계측하였다. 유속에 따라 고유주파수가 변하는 현상은 계측오차에 의한 것으로 제시하였다. 수중날개 유속이 증가하며 구조의 고유주파수가 증가하는 현상이 서로 다른 실험에서 공통적으로 나타나는 것을 보았을 때, 유속과 무관한 부가질량만 고려하여 수중 구조의 고유주파수를 예측할 수 없음을 확인할 수 있다. 구조시스템에 영향을 주어 고유주파수 변화를 야기할 수 있는 것은 부가질량과 함께 부가탄성이 있다. Chae et al.(12)과 Zhang et al.(17)은 공역학에서 제시된 Theodorsen 이론을 수중날개에 적용하여 유체-구조연성 해석을 수행하였다. Theodorsen 이론에 부가탄성 항이 존재하나 유속에 따른 고유주파수 변화를 구현하지 못함을 확인할 수 있다. Gauthier et al.(18)은 유속에 따라 변하는 수중날개 고유주파수 실험결과를 이용하여 날개에 작용하는 부가탄성을 역추정하였다. 유속별 고유주파수 데이터에 대하여 피팅(fitting)을 통해 부가탄성을 도출하였다. 하지만 수중날개 고유주파수에 대한 실험값이 존재해야 부가탄성을 도출할 수 있으며, 물리적 배경이 없는 데이터 피팅을 활용했기 때문에 다른 구조물에 대해서는 부가탄성을 예측할 수 없다. 따라서 일반적인 수중 구조물에 대하여 유속에 따른 부가탄성 도출 연구가 필요하다. 부가탄성을 수중 구조해석에 적용하면 유속에 따라 변하는 구조의 고유주파수를 예측할 수 있다.
이 연구에서는 수중날개에 대하여 유속에 따른 부가탄성을 도출하였다. 수중날개에 작용하는 유체동력학적 힘과 구조변위 사이 관계를 이용하여 유속에 따른 부가탄성 값을 계산하였다. 대상 날개에 대한 부가탄성을 도출하여 하이브리드 유체-구조연성 해석에 반영했으며, 연성 해석을 통해 수중날개의 고유주파수를 도출하였다. 해석을 통해 구한 날개의 고유주파수를 실험값과 비교하였으며 부가탄성 고려 유무에 따른 수중 구조 고유주파수 예측 정확도를 분석하였다.
2. 부가탄성 반영 하이브리드 유체-구조연성
2.1 하이브리드 유체-구조연성
유동환경 속 구조물은 주변 유체의 압력과 점성력에 의한 힘을 받는다. 구조는 유체동력학적 힘에 의해 변형이 일어나게 되며 유연체의 경우 변위가 반대로 주변 유동에 영향을 준다. 이와 같은 상호 연관성이 유체-구조연성이다.
유체동력학적 힘은 구조 표면에서의 압력과 점성력을 통해 구조로 전달된다. 반면 구조변위에 따른 영향은 구조물이 주변 유체를 밀어내며 나타난다. 따라서 유체와 구조의 경계면에서는 압력, 점성을 포함한 힘 성분과 속도가 일치한다. 유동의 경우 유속과 압력이 주요 변수이고 구조의 경우 변위가 주요 변수이기 때문에 유체와 구조의 경계면에서 각 변수에 대한 경계조건은 식 (1)과 (2)와 같다(8).
| (1) |
| (2) |
여기서 [σF]와 [σS]는 유체와 구조의 응력텐서를 의미하며, {vF}와 {vS}는 속도벡터를 의미한다. {n}는 유체와 구조 경계면에서의 법선단위벡터이다.
유체의 주요변수인 유속과 압력에 대한 지배방정식은 Navier-Stokes 방정식이며 일반적으로 대상 환경에 적합한 난류 모델링과 함께 CFD(computational fluid dynamics)를 이용하여 유동 예측을 한다. 반면 구조의 경우 FEM(finite element method)을 통해 구조를 이산화하여 거동을 예측한다. 구조의 FEM 지배방정식을 질량과 감쇄, 탄성행렬을 이용하여 표현하면 식 (3)과 같다.
| (3) |
여기서 [MS]와 [CS], [KS]는 각각 구조의 질량과 감쇄 그리고 탄성행렬을 의미한다. {δ}는 구조 노드 변위 벡터이며 윗첨자 점은 시간에 대한 미분을 의미한다. 식 (3)에서 우변은 구조에 작용하는 유체력에 대한 힘벡터로 압력에 의한 힘과 점성에 의함 힘을 모두 포함하고 있다. 경계조건 식 (1), (2)를 기반으로 구조해석과 유동해석을 개별적으로 수행하고 식 (3)을 기반으로 구조의 거동을 예측하는 방법이 분할 유체-구조연성(partitioned FSI) 해석이다(19).
유체동력학적 힘 성분 중 구조시스템에 영향을 주는 성분은 부가질량과 부가탄성이다. 부가질량은 유체동력학적 힘 성분 중 구조의 가속도와 위상이 같은 성분으로 구조의 질량이 증가하는 효과를 발생시킨다. 부가탄성의 경우 유체동력학적 힘 성분 중 구조변위와 위상이 같은 성분에 해당한다. 부가탄성은 구조의 탄성이 변화하는 효과를 일으킨다.
부가질량과 부가탄성은 구조의 형상과 주변 유체의 특성, 유동 환경에 의해서 결정된다. 대상 수중 구조의 부가질량과 부가탄성을 예측하여 구조시스템에 반영한 후 연성해석을 수행하는 방법이 하이브리드 유체-구조연성(hybrid FSI) 해석이다(19).
하이브리드연성은 식 (3)에서 우변에 있는 유체동력학적 힘 성분 중 부가질량과 부가탄성에 의한 영향을 좌변으로 이항하여 구조시스템의 일부로 해석을 수행한다. 하이브리드연성에 대한 구조 지배방정식은 식 (4)와 같다.
| (4) |
여기서 [MAdd]와 [KAdd]는 각각 구조에 작용하는 부가질량과 부가탄성이다. 분할연성과 하이브리드연성 모두 구조와 유동해석을 개별적인 해석시스템을 이용하여 유체-구조연성 해석을 수행한다. 하지만 두 기법에서 사용하는 구조시스템의 질량과 탄성행렬의 차이가 있다. 식 (5)와 (6)은 각각 분할연성과 하이브리드연성에 사용되는 구조 특성방정식이다.
| (5) |
| (6) |
여기서 λ는 특성방정식의 해다. 식 (5)와 (6)에서 특성방정식의 차이가 나타나는 것을 확인할 수 있으며, 이에 따라 구조 고유주파수 차이가 발생한다. 따라서 수중 구조물의 경우 부가질량과 부가탄성을 고려한 하이브리드연성을 적용해야 구조 거동을 정확하게 예측할 수 있다.
2.2 수중날개 부가탄성
부가탄성은 구조에 작용하는 유체동력학적 힘 성분 중 구조변위에 비례하는 성분을 의미한다. 부가탄성은 구조의 형상과 주변 유체의 특성 그리고 주변 유동 환경에 의해 결정된다. 대상 구조에 대한 부가탄성을 예측하고 이를 반영한 하이브리드연성 해석을 수행해야 수중 구조해석을 정확하게 수행할 수 있다.
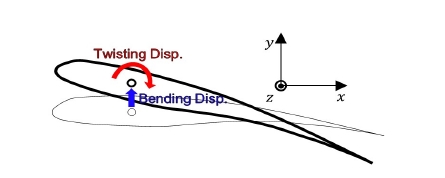
대상 수중날개의 부가탄성을 예측하기 위해서, 구조변위가 발생했을 때 나타나는 유체동력학적 힘의 변화를 파악했다. 수중날개에 대한 부가탄성 생성 경로를 도출하기 위해 날개의 거동을 굽힘과 비틀림 변위로 단순화했다. 날개 끝단의 단면 형상에 대하여 굽힘 변위와 비틀림 변위를 도식화하면 Fig. 1과 같다. Fig. 1과 같이 수중날개의 변위가 발생하면 날개 주변 유동장 변화가 발생한다.
유동장 변화에 따라 구조에 작용하는 유체동력학적힘이 변하게 된다. 날개단면에 작용하는 힘 중 회전모멘트는 날개의 받음각, 즉 비틀림 변위와 연관되어 있다. 회전모멘트는 실속이 일어나지 않는 범위 안에서 받음각에 비례하는 특성이 있다. 따라서 비틀림 변위에 따른 회전모멘트의 변화가 구조의 부가탄성으로 나타나게 된다.
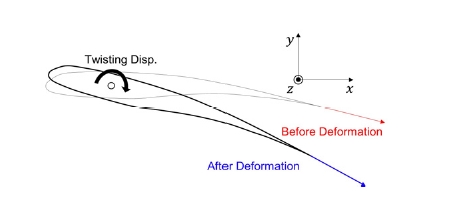
수중날개의 비틀림 변위가 발생하면 Fig. 2와 같이 주변 유동방향 변화가 발생한다. 구조변위에 의해 주변 유동방향이 바뀌면 유체운동량 변화가 발생한다. 유체운동량 변화는 구조에 작용하는 힘을 발생시킨다. Fig. 2에서와 같이 (-)z방향의 비틀림 변위가 일어나면 (-)y방향의 유체운동량이 증가한다. 이에 대한 반작용으로 구조 뒷날(trailing edge, TE)에는 (+)y방향 힘이 작용하게 되며, 이에 따라 (+)z방향 회전모멘트가 증가한다. 따라서 회전모멘트의 경우 (-)z방향 변위에 따라 (+)z방향 힘이 증가하기 때문에 양의 값의 부가탄성이 작용한다. 날개단면에 작용하는 회전모멘트는 실속하지 않는 받음각 범위 안에서 받음각에 비례하는 특성이 있다. 따라서 비틀림 변위에 따른 회전모멘트 변화를 도출하면 식 (7)과 같다.
| (7) |
여기서 M(θ)는 회전모멘트, ρF는 유체 밀도, U는 유속, S는 기준단면적, c는 코드(chord)길이, CM는 회전모멘트계수다. 식 (7)을 통해 회전모멘트에 대한 부가탄성은 유속의 제곱에 비례함을 확인할 수 있다. 따라서 유속이 빨라질수록 부가탄성의 영향이 증폭될 것을 예상할 수 있다. 부가탄성 값은 날개단면의 회전모멘트계수와 연관되어 있기 때문에 수중날개의 형상과 관련 있음을 알 수 있다. 식 (7)에서 부가탄성의 값이 유체의 밀도에 비례하는 것을 알 수 있으며, 밀도가 높은 수중 환경에서 부가탄성의 영향이 공기 중 대비 103오더로 크다. 따라서 수중 환경에서는 부가탄성에 의한 영향이 클 것을 예상할 수 있다.
수중날개에 작용하는 부가탄성값을 도출하기 위해 변위가 없을 때 구조에 작용하는 유체동력학적 힘과 변위가 발생했을 시 유체동력학적 힘을 유동해석을 통해 도출하였다. 이후, 변위에 따른 유체동력학적 힘의 변화 값이 부가탄성이며 해당 값을 유체-구조 경계에 적용하였다.
기존 수중날개 hybrid FSI 연구에서 적용한 부가탄성은 모두 Theodorsen 이론 바탕이다(12,17). Theodorson 이론 기반 부가탄성은 공기 중 평판을 가정하여 유도되었으며, 날개 두께에 따른 유체동력학적힘의 변화를 반영하지 못한다. 따라서 Theodorson 이론에 기반한 수중날개 hybrid FSI 해석을 수행한 경우 부가탄성에 의한 영향이 없는 것을 확인할 수 있다. 이 연구에서는 날개 두께를 포함한 임의의 형상에 작용하는 부가탄성 도출 방법을 제시했다. 평판 가정 없이 유속에 따른 부가탄성을 도출하고 이를 구조시스템에 반영하여 hybrid FSI 해석을 수행하였다.
3. 부가탄성 반영 수중날개 하이브리드연성 해석과 고유 응답
3.1 수중날개 하이브리드연성 해석
수중날개에 대하여 부가탄성 효과를 고려한 하이브리드연성 해석을 수행하였다. 유동해석의 경우 CFD를 이용하였으며, 구조해석의 경우 FEM을 적용하였다. Hybrid FSI 해석을 수행하기 위하여 상용 FEM 솔버 COMSOL을 이용하였다(20). 대상 수중날개의 코드길이는 250 mm이며, 알루미늄으로 이루어져 있다. 날개 단면은 Bergan et al.(16)이 실험을 수행한 형상과 동일하다. 실험에서는 150 mm × 150 mm 정사각형 단면의 파이프에 대상 형상을 외팔보로 고정하고 여러 유속조건에 대한 구조의 고유 응답을 계측하였다. 구조의 고유주파수를 계측하기 위하여, 압전소자(piezoelectric MFCs)와 LDV를 이용하였다. 각 유속조건에서 압전소자를 이용하여, 구조를 특정 주파수로 강제가진 시키고, LDV를 이용하여 구조의 응답을 계측하였다. 가진 주파수를 변경하며 구조 응답을 계측한 결과를 분석하여 응답 피크를 선별하고 해당 피크를 고유주파수로 제시하였다. 이 연구에서도 실험상황을 해석적으로 구현하기 위하여, 구조를 강제가진 시켰다. 구조 응답 피크 분석을 통해 고유주파수를 도출하였다.
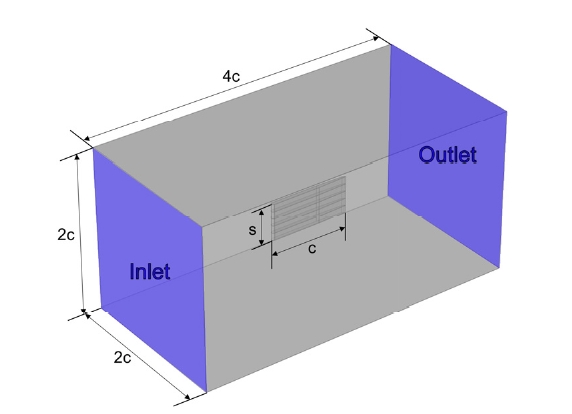
주변 유동과 코드의 방향은 (+)x방향이며, 스팬(span)방향은 (+)z방향이다. 해석에 사용된 구조와 유체 도메인은 Fig. 3과 같다. 날개 한쪽 끝은 고정되어 있는 외팔보 경계로 이루어져 있다.
유동장의 경우 유입면에 유속 경계조건을 부여했고, 반대면에는 압력경계조건을 적용하였다. 유체와 구조 경계에는 식 (1)과 식 (2)를 적용하였다.
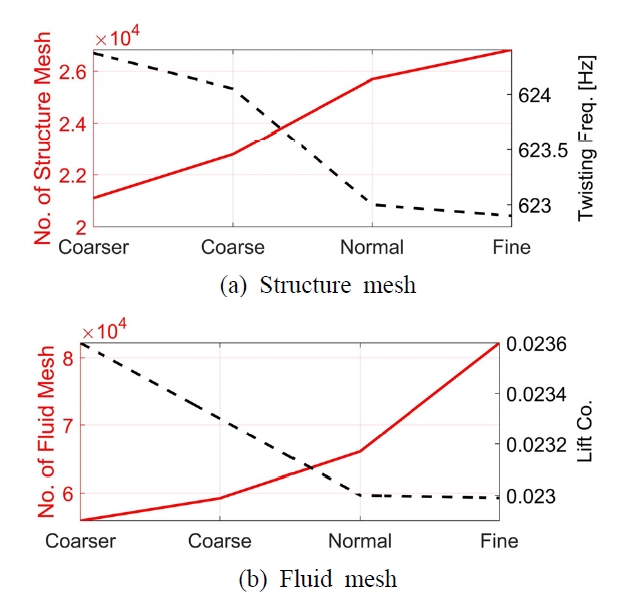
구조격자와 유동격자 모두 비정렬격자를 이용했으며 각각에 대하여 수렴성 검사를 진행하였다. 구조의 경우 고유주파수가 수렴하는 범위까지 격자수를 증가시켰다. 유동의 경우 날개에 작용하는 양력계수가 수렴하는 범위까지 격자수를 증가시켰다. 수렴성 검사 결과는 Fig. 4와 같다. Fig. 4(a)는 구조격자 수렴성 검사 결과이며, Fig. 4(b)는 유동격자 수렴성 검사 결과다. 구조와 유동격자 모두 격자밀도 노말(normal)수준에서 수렴하는 것을 확인할 수 있다. 해석에 사용된 구조와 유동격자 수는 각각 25 694개와 66 064개다. 해석 수렴성을 확보하기 위하여 초기에는 유동해석 단독으로 수행하고 유동이 수렴한 이후 하이브리드연성 해석으로 진입하는 방법을 사용하였다. t = 0 s에서 정상상태 유동해석을 수행하고 t = 0.1 s까지 비정상상태 유동해석을 수행하였다. t = 0.1 s 수준에서 유동해석이 수렴하는 것을 확인할 수 있었으며 t = 0.1 s에서 t = 1.2 s까지 ∆t=1E-4 s로 해석을 수행하였다. 시간간격과 해석 구간은 구조의 고유 응답 변화를 1 Hz해상도로 확인할 수 있는 조건으로 선정하였다.
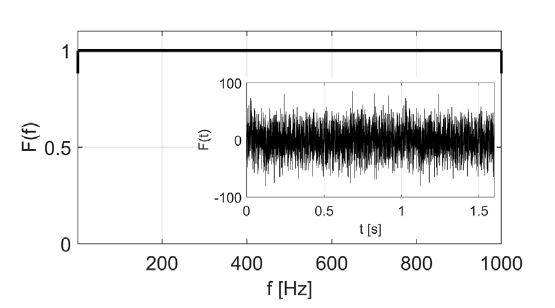
유속에 따른 부가탄성 변화를 파악하기 위하여 U={0, 5, 7.5, 10, 15, 20, 25} m/s에서 해석을 수행하였다. 각 유속에 대하여 부가탄성을 고려했을 때와 고려하지 않았을 때의 구조 고유주파수를 비교하였다. 이는 실험에서 압전소자를 이용해 구조 가진을 적용한 상황을 구현하기 위함이다. 해석에 적용한 강제가진력은 Fig. 5와 같다.
유동환경 속 수중날개 응답을 하이브리드연성 해석을 통해 도출하여 뒷날과 앞날(leading edge, LE)에서 응답을 추출하였다. TE와 LE에서의 구조 응답을 통해 수중날개의 비틀림 변위를 계산하였다. 비틀림 변위에 대한 주파수 분석을 통해 구조응답 피크가 발생하는 주파수 성분을 추출하여 구조의 고유주파수를 도출하였다. 해석을 통해 도출한 수중날개의 고유주파수를 실험값과 비교했으며, 부가탄성 고려 유무에 따른 해석결과를 분석하였다. 수중날개 부가탄성 값은 식 (7)을 기반으로 도출하였다. 비틀림비틀림 변위에 따른 회전모멘트의 값을 도출하고 식 (7)에 따른 회전모멘트와 부가탄성사이 관계를 이용하여 부가탄성을 계산하였다. 유속에 따른 부가탄성 변화를 고려하기 위하며 각 유속에 대한 회전모멘트 값을 도출하여 부가탄성을 도출하였다.
3.2 유속에 따른 수중날개 고유 응답 변화
수중날개 부가탄성은 유속의 제곱에 비례함을 식 (7)을 통해 확인할 수 있다. 또한 유속을 제외한 변수는 동일한 날개 구조에 대하여 상수임을 알 수 있다. 따라서 수중날개에 대한 부가탄성은 유속에 대한 함수다. 구조의 고유주파수는 모달질량(modal mass)과 모달탄성(modal stiffness)을 이용하여 식 (8)로 표현된다.
| (8) |
여기서 f는 고유주파수, K와 M는 각각 모달탄성과 모달질량이다. 식 (8)에서 수중 구조에 대한 부가질량과 부가탄성 효과를 반영하면 식 (9)와 같다.
| (9) |
여기서 KAdd와 MAdd는 각각 부가탄성과 부가질량이다. 식 (7)에서와 같이 부가탄성이 유속의 제곱에 비례하는 점을 식 (9)에 적용하여 정리하면 식 (10)과 같다.
| (10) |
식 (10)에서 U = 0 m/s이면 유속이 없는 조건에서 수중 고유주파와 동일하다. 따라서 수중날개 유속과 고유주파수 사이 관계는 최종적으로 식 (11)과 같다.
| (11) |
여기서 f0는 U = 0 m/s 조건에서 구조 고유주파수다. 식 (11)의 유효성을 확인하기 위해, 해당 식을 이용하여 유속에 따른 수중날개 고유주파수 실험값에 대한 추세식을 도출하였다. 대상 수중날개의 비틀림 응답 고유주파수의 값을 이용하여 추세식을 도출하면 Table 1과 같다. 식 (11)을 이용하여 추세식을 도출했을 때 b =51.21/m2가 된다. 변수 b는 날개 형상에 의존적인 변수로 해당 값은 이 연구의 대상 날개에 대한 값이며, 치수 변화가 나타난다면 b의 값 또한 변하게 된다. Table 1에서 각 유속에 대한 추세식의 값이 실험값과 잘 일치하는 것을 확인할 수 있다. 이를 통해 식 (7)과 같이 표현되는 수중날개의 부가탄성 값이 타당함을 알 수 있다. 대상 수중날개에 대하여 2.2절에서 제시한 방법을 통해 부가탄성을 계산하였으며 부가탄성 반영 유무에 따른 고유주파수 변화를 도출하였다.
3.3 부가탄성 반영 수중날개 고유 응답 특성
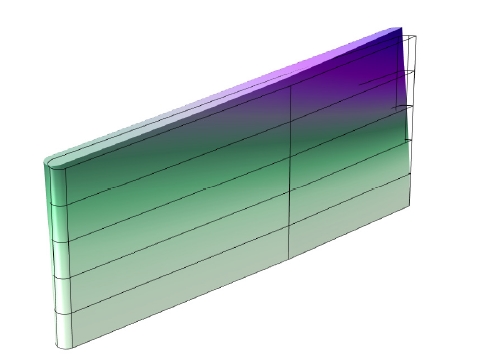
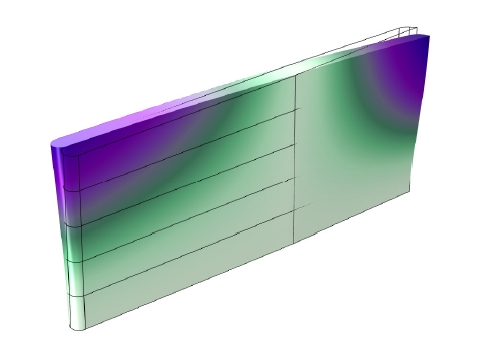
유속과 부가탄성 반영 여부에 따른 수중날개 고유주파수 변화 분석을 수행하였다. 대상 수중날개의 고유모드 형상을 파악하기 위해 U = 0 m/s조건 즉, 주변 유동이 없는 상황에서의 수중날개 고유응답 해석을 수행하였다. U = 0 m/s조건에서는 부가탄성의 영향이 없기 때문에 해석에 부가질량 효과만 반영되었다. Fig. 6과 Fig. 7은 각각 수중날개의 첫 번째 굽힘모드와 첫 번째 비틀림모드 형상이다. Fig. 6에서 굽힘모드의 경우 LE와 TE에서 응답의 위상이 동일함을 알 수 있다. 반면 Fig. 7에서 비틀림모드의 경우 LE와 TE에서 응답의 위상이 반대임을 알 수 있다. 따라서 LE와 TE에서 응답의 주파수 특성을 분석했을 때 나타나는 피크 중에서 서로간 위상이 동일하면 굽힘모드 응답이고 반대이면 비틀림모드 응답임을 알 수 있다.
Fig. 6에서 굽힘모드의 경우 히브(heave)방향, 즉 (+)y축 방향 변위가 발생했을 때, (+)z방향 비틀림 변위가 동시에 발생하는 것을 알 수 있다. 따라서 대상 날개구조의 경우 (+)y방향 굽힘 변위가 발생했을 때 받음각이 줄어드는 현상이 발생하고 이에 따라 양력이 감소하여 (-)y방향 힘이 증가하는 현상이 일어날 것을 예상할 수 있다. (+)y방향 변위에 따라 (-)y방향 힘이 증가하기 때문에 양의 값의 부가탄성이 작용한다. 따라서 유속에 따른 부가탄성을 반영했을 때 수중날개의 비틀림응답과 함께 굽힘응답 고유주파수 변화가 나타날 것을 예상할 수 있다.
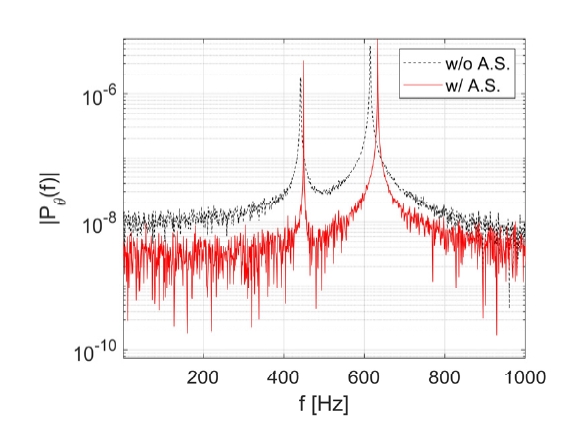
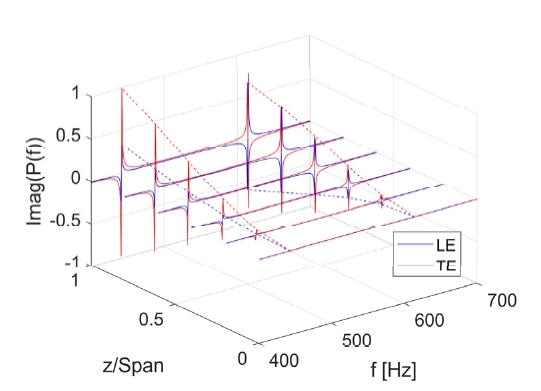
유속에 따른 수중날개의 고유주파수 분석을 수행하였다. U={0, 5, 7.5, 10, 15, 20, 25} m/s에 대해서 해석을 수행했으며 부가탄성을 고려했을 때와 반영하지 않았을 때의 구조 고유주파수를 도출하였다. LE와 TE에서 (+)y방향 변위를 추출하고 이를 이용하여 비틀림 변위를 도출하였다. 유속 U = 20 m/s에 대한 비틀림응답의 주파수 특성을 분석한 결과 Fig. 8과 같다. Fig. 8에서 검정색점선은 부가탄성을 고려하지 않았을 때, 빨간색실선은 부가탄성을 고려했을 때 주파수에 따른 비틀림응답 특성이다. 부가탄성을 반영함에 따라 고유주파수 변화가 나타나는 것을 확인할 수 있다. 1 Hz와 1 kHz사이 관심주파수 영역에서 비틀림응답 피크가 두 개 나타나는 것을 확인할 수 있다. 각 주파수에서 LE와 TE에서 응답의 위상 비교를 통해 해당 피크가 어떤 구조응답에 해당하는지 파악할 수 있다.
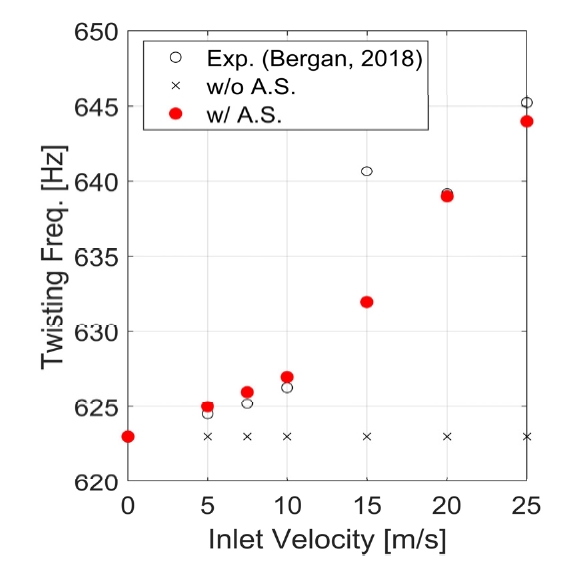
Fig. 9는 U = 20 m/s조건에 대하여, LE와 TE에서 (+)y방향 변위에 대한 위상을 주파수별로 도출한 결과다. Fig. 9에서 파란색선은 LE에서 구조 응답의 위상 정보이고 빨간색선은 TE에서 위상 정보이다. 첫 번째 피크에서는 LE와 TE에서 위상이 동일한 것을 확인할 수 있다. 둘 사이 위상이 동일하다는 것은 해당 주파수가 굽힘응답에 해당함을 의미한다. 반면 두 번째 피크에서 LE와 TE에서의 위상이 반대임을 알 수 있다. 따라서 두 번째 피크는 구조의 비틀림모드에 해당하는 것을 파악할 수 있다. 해석을 수행한 모든 유속에 대하여 동일한 과정을 거쳐 수중날개의 굽힘응답과 비틀림응답 주파수를 도출하였다. 각 유속에 대하여 부가탄성 고려 유무에 따른 고유주파수를 도출하고 실험값과 비교하였다. U={0, 5, 7.5, 10, 15, 20, 25} m/s에 대하여 하이브리드연성 해석을 통해 구한 수중날개의 고유주파수는 Fig. 10과 같다. Fig. 10에서 검정색원은 실험결과이다. 빨간색원은 부가탄성을 고려한 하이브리드연성 해석을 통해 도출한 수중날개의 비틀림 고유주파수다. 검정색곱표는 부가탄성을 고려하지 않은 해석에서 도출한 비틀림 고유주파수다.
부가탄성을 고려하지 않았을 때는 유속 변화에 따른 효과가 구조해석에 반영되지 않아 유속이 증가함에도 고유주파수가 일정한 것을 알 수 있다. 반면 부가탄성을 고려했을 시에는 유속에 의한 효과가 구조시스템에 반영되어 유속이 증가함에 따라 비틀림 고유주파수가 증가하는 것을 확인할 수 있다. 이와 같이 증가하는 경향은 실험에서도 동일하게 나타난다. 각 유속에 대한 고유주파수를 비교해보면, 부가탄성을 고려했을 때 해석 결과가 실험값과 잘 일치하는 것을 알 수 있다.
단, U=15 m/s 조건에서는 부가탄성을 반영한 해석결과와 실험결과와 차이가 발생하는 것을 확인 할 수 있다. 이는 lock-in 구간에서 lock-off 구간으로 전환되며 나타나는 현상이다.
Zobeiri et al.(21)과 Ausoni(22)가 수행한 수중날개 실험 결과를 통해 lock-in 구간과 lock-in에서 lock-off으로 전환되는 조건에서 나타나는 구조응답과 와류박리 특성이 lock-off 구간에서 나타나는 경향과 상이함을 알 수 있다. 이 연구에서 비교 분석한 Bergan et al.의 실험 결과에서는 U=15 m/s 조건에서 lock-in에서 lock-off 영역으로 전환되며 lock-off 구간에서 나타나는 구조응답의 특성과 차이가 발생한 것으로 판단된다. 따라서 식 (7)에서 제시한 수중날개의 부가탄성은 lock-off 구간에서 유효함을 알 수 있고, lock-in 조건과 lock-in에서 lock-off으로 전환되는 유속 조건에서 변화를 예측하기 위해서는 추가적인 연구가 필요하다.
Table 2는 비틀림모드에 대하여 부가질량과 부가탄성 값이다. Table 2에서 Fig. 10에서와 같이 유속이 증가함에 부가탄성값이 증가하는 것을 확인할 수 있고 이는 식 (7)을 통해서 예측할 수 있는 결과와 일치한다. 따라서 높은 유속에서는 부가탄성의 영향이 증폭되며, 부가탄성을 고려한 하이브리드연성 해석을 수행하여 유속에 따라 수중날개의 비틀림모드 주파수가 변하는 특성을 해석에 반영할 수 있다.
앞서 Fig. 6에서 굽힘모드가 일어남에 따라 비틀림모드 특성도 나타나는 것을 보았을 때, 굽힘모드에 대해서도 유속에 따른 고유주파수 변화가 나타날 것이다. Table 3는 U={0, 5, 7.5, 10, 15, 20, 25} m/s유속에 대하여 수중날개의 굽힘모드 고유주파수를 도출한 결과다.
Table 3에서 예상했던 바와 같이 유속이 증가하며 수중날개의 굽힘모드 고유주파수가 증가하는 것을 확인할 수 있다. 이는 대상 날개의 (+)y방향 굽힘 변위가 (+)z방향 비틀림 변위와 연성되어 있기 때문에 나타나는 현상이다. Table 2와 Fig. 10에서의 굽힘과 비틀림모드 고유주파수를 보았을 때 비틀림모드가 굽힙모드 대비 유속 영향을 더 받는 것을 알 수 있다. 수중 구조가 부가탄성에 의한 영향을 크게 받기 위해서는 구조변위에 따른 유체동력학적힘의 변화가 커야한다. 대상 수중날개의 경우 굽힘보다 비틀림 변위가 일어났을 때 상대적으로 유체동력학적힘의 변화가 크게 일어나기 때문에 이와 같은 현상이 나타났다.
4. 결 론
이 연구에서는 수중날개 주변 유동에 의한 탄성효과를 구조시스템에서의 부가탄성으로 고려하였다. 부가탄성을 하이브리드연성 해석에 반영하며 유속 변화에 따른 수중 구조 고유주파수 변화를 해석적으로 구현하였다. 기존에는 수중 구조에 대한 부가질량을 예측하여 하이브리드연성 해석에 반영하였다. 하지만 부가탄성 없이 부가질량만 고려하면 유속이 변함에 따라 구조의 고유 응답이 변화하는 특징을 구현할 수 없다.
수중날개 단면에 작용하는 유체동력학적 힘과 구조변위 그리고 유속사이 관계를 도출하여 유속별로 구조에 작용하는 부가탄성을 도출하였다. 부가탄성을 반영한 하이브리드연성 해석을 수행한 결과 유속이 증가함에 따라 수중날개 고유주파수가 증가하는 실험값과 일치하는 것은 확인하였다. 수중 구조에 작용하는 부가탄성의 영향은 유속이 빨라짐에 따라 증가하는 것을 확인하였다. 따라서 높은 유속에서 작동하는 수중 구조의 응답을 예측하기 위해서 부가질량과 함께 부가탄성을 고려해야한다.
Acknowledgments
이 연구는 서울대학교 BK21 해양플랜트 창의인재 양성사업단의 지원을 받아 수행하였습니다. 또한, 해양시스템공학연구소(RIMSE) 및 연구재단(2019R1F1A1062914)의 지원을 받아 수행하였습니다.
References
-
Lee, Y.-J., Jhan, Y.-T. and Chung, C.-H., 2012, Fluid-structure Interaction of FRP Wind Turbine Blades under Aerodynamic Effect, Composites Part B: Engineering, Vol. 43, No. 5, pp. 2180~2191.
[https://doi.org/10.1016/j.compositesb.2012.02.026]

-
Huang, Z., Xiong, Y. and Xu, Y., 2019, The Simulation of Deformation and Vibration Characteristics of a Flexible Hydrofoil based on Static and Transient FSI, Ocean Engineering, Vol. 182, pp. 61~74.
[https://doi.org/10.1016/j.oceaneng.2019.04.028]

-
Oh, S.-W., Park, O. and Kim, D.-H., 2006, Flow-induced Vibration Analysis for Cascades with Stator-rotor Interaction and Viscosity Effect, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 10, pp. 1082~1089.
[https://doi.org/10.5050/KSNVN.2006.16.10.1082]

-
Kim, Y.-S., Kim, D.-H., Kim, Y.-H. and Park, O., 2009, Fluid/Structure Coupled Analysis of 3D Turbine Blade Considering Stator-rotor Interaction, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 8, pp. 764~772.
[https://doi.org/10.5050/KSNVN.2009.19.8.764]

-
Zhu, J., Cai, X. and Gu, R., 2016, Aerodynamic and Structural Integrated Optimization Design of Horizontal-axiswind Turbine Blades, Energies, Vol. 9, No. 2, pp. 1~18.
[https://doi.org/10.3390/en9020066]

-
Lee, H., Song, M.-C., Han, S., Chang, B.-J. and Suh, J.-C., 2017, Hydro-elastic Aspects of a Composite Marine Propeller in Accordance with Ply Lamination Methods, Journal of Marine Science and Technology, Vol. 22, No. 3, pp. 479~493.
[https://doi.org/10.1007/s00773-016-0428-4]

-
Liang, Q. W., Rodriguez, C. G., Egusquiza, E., Escaler, X., Farhat, M. and Avellan, F., 2007, Numerical Simulation of Fluid added Mass Effect on a Francis Turbine Runner, Computers & Fluids, Vol. 36, No. 6, pp. 1106~1118.
[https://doi.org/10.1016/j.compfluid.2006.08.007]

-
Wright, J. R., and Cooper, J. E., 2015, Introduction to Aircraft Aeroelasticity and Loads, John Wiley & Sons, Inc., Chichester.
[https://doi.org/10.1002/9781118700440]

-
Zarruk, G. A., Brandner, P. A., Pearce, B. W. and Phillips, A. W., 2014, Experimental Study of the Steady Fluid-structure Interaction of Flexible Hydrofoils, Journal of Fluids and Structures, Vol. 51, pp. 326~343.
[https://doi.org/10.1016/j.jfluidstructs.2014.09.009]

-
Liao, Y., Garg, N., Martins, J. R. R. A. and Young, Y. L., 2019, Viscous Fluid-structure Interaction Response of Composite Hydrofoils, Composite Structures. Vol. 212, pp. 571~585.
[https://doi.org/10.1016/j.compstruct.2019.01.043]

-
Zeng, Y., Yao, Z., Gao, J. Hong, Y., Wang, F. and Zhang, F., 2019, Numerical Investigation of Added Mass and Hydrodynamic Damping on a Blunt Trailing Edge Hydrofoil, Journal of Fluids Engineering, Vol. 141, No. 8, pp. 1~13.
[https://doi.org/10.1115/1.4042759]

-
Chae, E. J., Akcabay, D. T., Lelong, A., Astolfi, J. A. and Young, Y. L., 2016, Numerical and Experimental Investigation of Natural Flow-induced Vibrations of Flexible Hydrofoils, Physics of Fluids, Vol. 28, No. 7, p. 075102.
[https://doi.org/10.1063/1.4954785]

-
Li, J., Qu, Y., Zhang, Z. and Hua, H., 2020, Parametric Analysis on Hydroelastic Behaviors of Hydrofoils and Propellers Using a Strongly Coupled Finite Element/panel Method, Journal of Marine Science and Technology, Vol. 25, No. 1, pp. 148~161.
[https://doi.org/10.1007/s00773-019-00638-z]

-
Seeley, C., Coutu, A., Monette, C., Nennemann, B. and Marmont, H., 2012, Characterization of Hydrofoil Damping due to Fluid-structure Interaction Using Piezocomposite Actuators, Smart Materials and Structures, Vol. 21, No. 3, p. 035027.
[https://doi.org/10.1088/0964-1726/21/3/035027]

-
Yao, Z., Wang, F., Dreyer, M. and Farhat, M., 2014, Effect of Trailing Edge Shape on Hydrodynamic Damping for a Hydrofoil, Journal of Fluids and Structures, Vol. 51, pp. 189~198.
[https://doi.org/10.1016/j.jfluidstructs.2014.09.003]

-
Bergan, C. W., Solemslie, B. W., Østby, P. and Dahlhaug, O. G., 2018, Hydrodynamic Damping of a Fluttering Hydrofoil in High-speed Flows, International Journal of Fluid Machinery and Systems, Vol. 11, No. 2, pp. 146~153.
[https://doi.org/10.5293/IJFMS.2018.11.2.146]

-
Zhang, M., Liu, T., Huang, B., Wu, Q. and Wang, G., 2020, Hydrodynamic Characteristics and Flow Structures of Pitching Hydrofoil with Special Emphasis on the Added Force Effect, Renewable Energy, Vol. 157, pp. 560~573.
[https://doi.org/10.1016/j.renene.2020.05.081]

-
Gauthier, J. P., Giroux, A. M., Etienne, S. and Gosselin, F. P., 2017, A Numerical Method for the Determination of Flow-induced Damping in Hydroelectric Turbines, Journal of Fluids and Structures, Vol. 69, pp. 341~354.
[https://doi.org/10.1016/j.jfluidstructs.2017.01.004]

-
Young, Y. L., Chae, E. J. and Akcabay, D. T., 2012, Hybrid Algorithm for Modeling of Fluid-structure Interaction in Incompressible, Viscous Flows, Acta Mechanica Sinica, Vol. 28, No. 4, pp. 1030~1041.
[https://doi.org/10.1007/s10409-012-0118-3]

- Multuphysucs, C.O.M.S.O.L, 2013, Comsol Multiphysics Reference Manual (Version 4.3b), COMSOL, Grenoble, France.
-
Zobeiri, A., Ausoni, P., Avellan, F. and Farhat, M., 2012, How Oblique Trailing Edge of a Hydrofoil Reduces the Vortex-induced Vibration, Journal of Fluids and Structures, Vol. 32, pp. 78~89.
[https://doi.org/10.1016/j.jfluidstructs.2011.12.003]

- Ausoni, P., Avellan, F. and Farhat, M., 2009, Turbulent Vortex Shedding from a Blunt Trailing Edge Hydrofoil, EPFL Scientific Publication.

Beom-Jin Joe received the B.S. degree in Naval Architecture and Ocean Engineering from the Seoul National University, Korea, in 2018. He is currently working toward the Ph.D. degree in noise and vibration at Seoul National University. He is especially interested in predicting response of underwater structures using FSI analysis.

Jee-Hun Song received his B.S. degree in Naval Architecture and Ocean Engineering from the Seoul National University, Korea, in 2003, and his Ph.D. in 2007. Currently he is a professor of Naval Architecture and Ocean Engineering at Chonnam National University, Korea. His primary research interest is vibration and noise analysis in structures.