유동환경을 고려한 탄성공명패널의 흡음특성에 관한 연구

1. 서 론

국내 고속철도의 최대속도는 300 km/h이며 지속전인 기술발전에 따른 향후 속도 증가를 고려했을 때 철도소음의 증가는 필연적으로 발생한다. 최고 시험속도 400 km/h에서 운행할 수 있는 차세대 고속철도가 개발됨에 따라 유동환경에서 발생하는 철도소음을 저감할 수 있는 방안에 대한 연구가 필요한 실정이다. 탄성공명패널은 미세천공판, 공동, 후판으로 구성된 구조물이며 해당 패널은 설계변수에 따라 목표 주파수 소음을 저감할 수 있는 장점을 가진다. 이에 따라 탄성공명패널은 철도소음에 대한 저감방안으로써 주목을 받고 있으며, 현재 국내외에서 해당 패널에 대한 연구를 활발히 수행하고 있다.

탄성공명패널은 헬름홀츠 공진(Helmholtz resonance)에 의한 흡음 메커니즘을 가진다^(1~3). 해당 메커니즘 바탕의 흡음성능을 예측하기 위한 연구가 활발히 이루어지고 있다. Maa^(4,5)는 최초로 탄성공명패널을 흡음구조로써 제시하였으며 탄성공명패널의 이론적 기반과 발전가능성에 대해 제시하였다. Lee et al.⁽⁶⁾은 패널의 진동이 흡음성능에 영향을 미침을 실험 및 해석적으로 도출하였다. Sakagami et al.⁽⁷⁾은 이중 미세천공판으로 구성된 탄성공명패널을 제시하였으며 저주파수 대역에서의 추가적인 흡음성능을 확인하였다. Toyoda et al.⁽⁸⁾은 허니컴을 포함한 탄성공명패널에 대한 흡음성능해석을 수행하고 실험결과와 비교검증을 수행하였으며 중주파수 대역에서의 흡음성능 향상을 확인하였다. Park et al.⁽⁹⁾은 기존 비선형 임피던스 모델을 바탕으로 설계변수에 따른 탄성공명패널의 흡음 특성 변화를 확인하였다. 이처럼 탄성공명패널에 대한 흡음성능을 예측하기 위한 연구가 지속적으로 활발히 이루어졌으나 유동환경을 고려한 탄성공명패널에 대한 연구는 미미한 실정이다.

유동환경을 고려한 탄성공명패널의 흡음성능에 대한 연구는 탄성공명패널의 기하학적 특성에 의해 어려움을 갖는다. 탄성공명패널의 천공이 1 mm 이하로 굉장히 작은 기하특성을 가짐에 따라 직접적으로 천공을 모델링하여 유동환경에서의 흡음성능을 해석하는 것이 어려운 실정이다. 해당 천공을 직접적으로 모델링 한 후 전산유체역학(computational fluid dynamics, CFD) 및 음향해석(acoustic analysis)을 통하여 유동환경에서의 흡음성능을 도출할 수 있다면 패널 주변에서 발생하는 유동 현상들을 직접적으로 구현할 수 있다는 장점을 가지지만 직접 모델링의 어려움이 있을 뿐만 아니라 전산유체역학을 기반으로 해당 천공에 대해 유동환경에 대한 해석을 수행할 때 계산비용이 기하급수적으로 증가하는 단점을 가진다. 따라서, 유동환경을 고려한 탄성공명패널의 흡음성능을 예측할 수 있는 이론 바탕의 예측기법에 대한 연구가 우선적으로 수행되어야하며 정립된 예측기법 바탕의 유동환경기반 탄성공명패널의 흡음특성 연구가 필요하다.

이 논문에서는 음향 임피던스 모델 이론 기반의 유동환경을 고려한 탄성공명패널 흡음성능예측기법을 정립하고 해당 이론 바탕의 흡음특성 연구를 수행하였다. 유동환경이 반영된 탄성공명패널의 음향 임피던스 모델을 탄성공명패널 흡음성능예측 이론에 반영하여 흡음성능을 도출하였으며 흡음 피크에 대한 strouhal 수 및 흡음 스펙트럼에 대한 실험결과와 비교검증함으로써 해당 방법에 대한 타당성을 검증하였다. 검증된 이론 기반의 방법을 바탕으로 설계변수에 따른 탄성공명패널의 흡음성능을 분석하였다. 분석결과를 바탕으로 설계 기준 공극률을 도출하였으며 철도소음의 저주파수 대역 소음을 저감시킬 수 있는 탄성공명패널의 설계방안을 제시하였다.

2. 유동환경을 고려한 탄성공명패널 흡음성능예측 이론

2.1 유동환경을 고려한 음향 임피던스

유동환경은 고속 철도환경과 동일하게 패널 외부로의 접선유동(grazing flow)이 분포하는 환경을 가정한다. 유동환경을 고려한 탄성공명패널의 흡음성능은 패널 주변의 유동환경의 영향을 반영한 음향 임피던스를 적용함으로써 도출할 수 있다. 해당 유동환경의 영향을 반영한 음향 임피던스는 실험적으로 유동환경을 구현함으로써 다양한 조건 하에서 도출되었다. 기존 탄성공명패널에 대한 음향 임피던스는 Maa^(4,5)에 의해 도출되었으며 식 (1)과 같다.

$\[ z_0\begin{array}{l}=\frac{32\eta t_h}{d_h^2}\left[\sqrt{1 +\frac{k_h^2}{32}}+\frac{\sqrt{2}}{8}\frac{d_h{k}_h}{t_h}\right]\\ -j{\rho }_0\omega t_h\left[1+{\left(9+\frac{k_h^2}{2}\right)}^{-\frac{1}{2}}+0.85\frac{d_h}{t_h}\right]\end{array} \]$

(1)

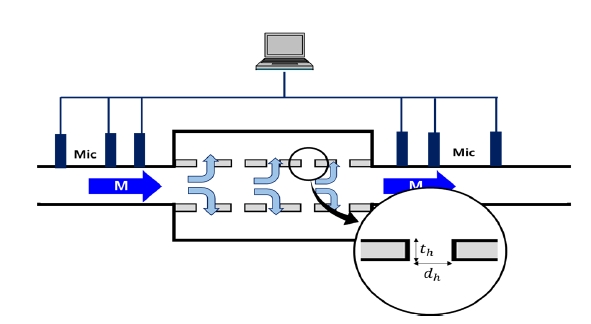
여기서, k_h는 $$ d_h\sqrt{{\rho }_0\omega {\eta }^{-1}/2}$$에 해당하는 상수이며, η, ρ₀는 각각 공기중 점성계수와 밀도를 나타낸다. t_h, d_h는 각각 탄성공명패널의 두께 및 천공직경을 나타낸다. 식 (1)은 주변 유동이 없을 때의 탄성공명패널의 음향 임피던스를 나타낸다. Fig. 1과 같이 실험적으로 도출된 유동환경의 영향에 따른 음향 임퍼던스의 변화를 식 (1)에 반영함으로써 식 (2)의 유동환경을 고려한 음향 임피던스가 도출된다^(10~13).

$\[ z_f\begin{array}{l}=\frac{32\eta t_h}{d_h^2}\left[\sqrt{1 +\frac{k_h^2}{32}}+\frac{\sqrt{2}}{8}\frac{d_h{k}_h}{t_h}\right]+{\rho }_0{c}_{0}KM\\ -j{\rho }_0\omega t_h\left[1+{\left(9+\frac{k_h^2}{2}\right)}^{-\frac{1}{2}}+0.85\frac{d_h}{t_h}F\left(M\right)\right]\end{array} \]$

(2)

Fig. 1

Reference apparatus for microperforated panel impedance

여기서, ρ₀c₀KM은 탄성공명패널 주변에 접선유동환경이 반영됨에 따라 추가적으로 발생한 음향 레지스턴스(resistatance)에 해당하며 M은 마하수(Mach number), K는 0.15로 실험적으로 도출된 상수에 해당한다. F(M)은 실험적으로 도출된 음향 리액턴스(reactance)의 변화를 나타내며 (1+(12.6M)³)^-1에 해당한다. 기존 탄성공명패널의 음향 임피던스 모델을 바탕으로 유동영향에 따른 임피던스의 변화를 반영함으로써 유속에 따른 음향 임피던스값이 도출된다. 이 논문에서는 해당 임피던스값을 바탕으로 유동환경을 고려한 탄성공명패널에 대한 흡음성능 예측을 수행하였다.

2.2 탄성공명패널 흡음성능예측 이론

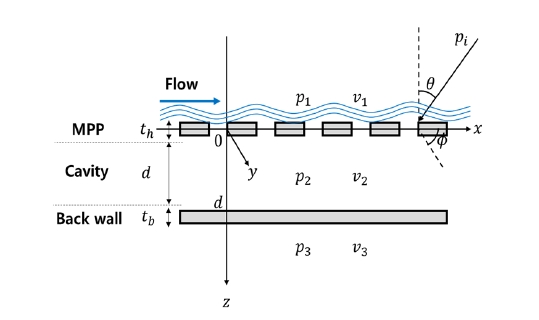
유동환경을 고려한 음향 임피던스 모델을 탄성공명패널 흡음성능예측 이론⁽⁸⁾에 적용하였다. 해당 탄성공명패널 흡음성능예측 이론은 패널을 기준으로 입사파, 반사파, 투과파 및 패널 거동 사이의 관계를 규명하고 최종적으로 패널의 흡음성능을 도출하는 이론에 해당한다. Fig. 2는 입사파를 기준으로 패널 주변에 형성되는 음압 및 속도 분포를 나타낸다. 각 수식에서의 아래 첨자 1, 2, 3은 각각 미세천공판, 공동, 후판을 의미한다. z축 수직법선을 기준으로 θ의 입사각을 가지며 진폭이 1인 입사파와 패널 주변 음압 분포는 식 (3) ~ 식 (5)으로 표현된다⁽¹⁴⁾.

$\[ p_i\left(x,z\right)=e^{{ik}_0\left(\mathrm{s}\mathrm{i}\mathrm{n}\theta x+ \mathrm{c}\mathrm{o}\mathrm{s}\theta z\right)} \]$

(3)

$\[ p_1\left(x\right)=2p_i\left(x,0\right)-\frac{{\rho }_0\omega }{2}{\int }_{-\infty }^{\infty }{H}_0^{\left(1\right)}\left(k_0\left|x-x_0\right|\right)v_1\left(x_0\right){dx}_0 \]$

(4)

$\[ p_3\left(x\right)=\frac{{\rho }_0\omega }{2}{\int }_{-\infty }^{\infty }{H}_0^{\left(1\right)}\left(k_0\left|x-x_0\right|\right)v_3\left(x_0\right){dx}_0 \]$

(5)

Fig. 2

Analytical model

여기서, ρ₀는 공기에 대한 밀도를 나타내며 v₁과 v₃는 각각 해당 위치에서의 입자속도(particle velocity)를 나타낸다. 공동 내부 음압과 속도는 식 (6)과 식 (7)로 도출된다.

$\[ p_2\left(x,z\right)=\left(P^{+}{e}^{{ik}_0\mathrm{c}\mathrm{o}\mathrm{s}\theta z}+P^{-}{e}^{-{ik}_0\mathrm{c}\mathrm{o}\mathrm{s}\theta z}\right)e^{{ik}_0\mathrm{s}\mathrm{i}\mathrm{n}\theta x} \]$

(6)

$\[ v_2\left(x,z\right)=\frac{\mathrm{c}\mathrm{o}\mathrm{s}\theta }{{\rho }_0{c}_0}\left(P^{+}{e}^{{ik}_0\mathrm{c}\mathrm{o}\mathrm{s}\theta z}-P^{-}{e}^{-{ik}_0\mathrm{c}\mathrm{o}\mathrm{s}\theta z}\right)e^{{ik}_0\mathrm{s}\mathrm{i}\mathrm{n}\theta x} \]$

(7)

여기서, P^±는 공동 내부에서 양방향으로 전파되는 음압의 진폭을 각각 나타내며 c₀는 공기중 음속을 나타낸다. 패널 내부와 외부의 음압 차로 인해 외력이 발생하게 되며 해당 힘으로부터 패널의 거동이 발생한다. 해당 힘으로부터 발생한 패널 거동에 대한 운동방정식은 식 (8)과 같다.

$\[ \frac{{\partial }^{4}u\left(x\right)}{\partial x^4}-k^{4}u\left(x\right)=\frac{\delta \left(x\right)}{D_f} \]$

(8)

여기서, k, D_f는 각각 탄성파에 대한 파수와 굽힘 강성(flexural rigidity)을 나타낸다. u(x)는 δ(x)의 단위 가진이 패널에 작용했을 때 발생하는 변위를 나타낸다. 탄성공명패널이 미세천공판과 후판을 포함하기 때문에 식 (8)을 각 패널에 각각 적용해야되며 이로부터 미세천공판과 후판에 대한 변위가 각각 도출된다. δ(x)의 단위 가진으로부터 도출된 미세천공판과 후판에 대한 변위가 u₁과 u₂ 일 때 각 패널 내외부의 음압 차이로부터 도출되는 미세천공판과 후판에 대한 변위는 합성곱(convolution)을 통해 식 (9)와 식 (10)과 같이 도출된다⁽⁸⁾.

$\[ w_1\left(x\right)={\int }_{-\infty }^{\infty }\left\{p_1\left(\xi \right)-p_2\left(\xi ,0\right)\right\}{u}_1\left(x-\xi \right)d\xi \]$

(9)

$\[ w_2\left(x\right)={\int }_{-\infty }^{\infty }\left\{p_2\left(\xi ,d\right)-p_3\left(\xi \right)\right\}{u}_2\left(x-\xi \right)d\xi \]$

(10)

미세천공판과 후판 간의 속도 경계조건은 각 패널 내부, 외부에서의 속도 연속성 조건에 해당하며 해당 조건은 식 (11)과 식 (12)로 표현된다⁽¹⁵⁾.

$\[ v_1\begin{array}{l}=\left(x\right)=v_2\left(x,0\right)\\ =-i\omega \zeta w_1\left(x\right)+\frac{\sigma }{z_f}\left\{p_1\left(x\right)-p_2\left(x,0\right)\right\}\end{array} \]$

(11)

$\[ v_2\left(x,d\right)=-i\omega w_2\left(x\right) \]$

(12)

여기서, σ는 미세천공판의 공극률에 해당하며 ξ는 1-(z_react/z_f)σ로 표현된다. z_f는 유동환경을 고려한 탄성공명패널의 음향 임피던스를 나타내며 z_react는 z_f의 허수부에 해당한다. 이 논문에서는 식 (2)의 음향 임피던스 모델을 식 (11)의 임피던스항에 적용함으로써 유동환경에 의한 영향을 반영하였다.

식 (4) ~ 식 (7), 식 (8) ~ 식 (10)을 정리하여 속도 연속성 경계조건인 식 (11)과 식 (12)에 대입하면 미세천공판과 후판 내외부의 속도에 대한 식 (13)과 식 (14)를 도출할 수 있다.

$\[ v_1\left(x\right)=Q_v\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)\mathrm{c}\mathrm{o}\mathrm{s}\theta e^{{ik}_0\mathrm{s}\mathrm{i}\mathrm{n}\theta x}/\left({\rho }_0{c}_0\right) \]$

(13)

$\[ v_3\left(x\right)=-i\omega F_2\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)e^{{ik}_0\mathrm{s}\mathrm{i}\mathrm{n}\theta x} \]$

(14)

여기서, Q_v, F₂는 식 (4) ~ 식 (7)을 속도 연속성 경계조건 식 (9)와 식 (10)에 대입함으로써 도출된 변수들에 해당하며 각각 미세천공판과 후판 외부의 속도 진폭을 나타낸다. 입사파와 반사파에 대한 인텐시티는 각각 식 (15)와 식 (16)으로 표현된다.

$\[ I_i=\frac{\mathrm{c}\mathrm{o}\mathrm{s}\theta }{2{\rho }_0{c}_0} \]$

(15)

$\[ I_r\begin{array}{l}=\frac{1}{2}Re\left[\left\{p_1\left(x\right)-p_i\left(x,0\right)\right\}\right.\\ \left.•{\left\{-v_1\left(x\right)+v_i\left(x,0\right)\right\}}^{\mathrm{*}}\right]\\ =\frac{\mathrm{c}\mathrm{o}\mathrm{s}\theta }{2{\rho }_0{c}_0}Re\left[Q_p\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)-1\right.\\ \left.•{\left\{-Q_v\left(k_0\mathrm{s}\mathrm{i}\mathrm{n}\theta \right)+1\right\}}^{\mathrm{*}}\right]\end{array} \]$

(16)

여기서, Q_p는 미세천공판 외부의 음압 진폭을 나타낸다. 해당 인텐시티를 바탕으로 유동환경을 고려한 탄성공명패널에 대한 흡음률을 도출할 수 있으며 해당 흡음률은 식 (17)과 식 (18)과 같다.

$\[ \alpha =1-\frac{I_r}{I_i} \]$

(17)

$\[ \overline{\alpha }=10{\mathrm{l}\mathrm{o}\mathrm{g}}_{10}\frac{2{\int }_0^{\pi /2}{\int }_0^{{\theta }_{\mathrm{l}\mathrm{i}\mathrm{m}}}\alpha \mathrm{s}\mathrm{i}\mathrm{n}2\theta d\theta d\varphi }{\pi {\int }_0^{{\theta }_{\mathrm{l}\mathrm{i}\mathrm{m}}}\mathrm{s}\mathrm{i}\mathrm{n}2\theta d\theta } \]$

(18)

식 (17)은 단일 입사각에 대한 흡음률을 나타내며, 식 (18)은 모든 입사각에 대한 평균 흡음률을 나타낸다. 최종적으로 도출된 흡음률식은 음향 임피던스 모델을 적용함에 따라 유동환경을 고려한 탄성공명패널의 흡음률을 나타내며 이 식을 바탕으로 다양한 유동 조건에서의 탄성공명패널에 대한 흡음성능 특성분석이 가능하다.

3. 유동환경을 고려한 탄성공명패널 흡음성능

3.1 탄성공명패널 제원 및 검증

유동환경에서의 흡음성능 도출을 위한 탄성공명패널의 제원과 물성치는 Table 1과 같다. 해당 탄성공명패널은 미세천공판, 공동, 후판으로 구성된 단층 탄성공명패널이며 각 패널의 재질은 모두 알류미늄으로 구성되었다. 각 패널은 매질과 두께만을 포함하는 무한 평판임을 가정하였다. 고속철도 환경과 동일하게 미세천공판 외부에 유속이 분포하도록 Fig. 2와 같이 모델을 구성하였으며 해당 패널을 기준으로 유속, 천공직경, 공극률에 따른 흡음성능 도출하였다.

Table 1

Each panel information

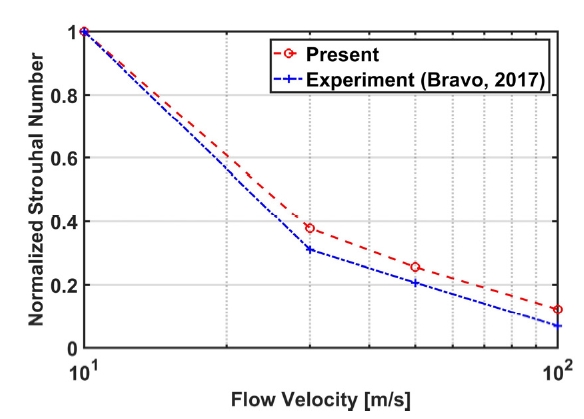
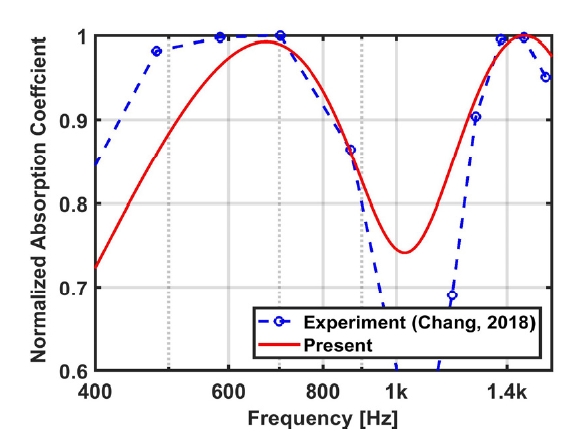
탄성공명패널은 천공과 공동을 포함함에 따라 헬름홀츠 공진에 의한 흡음 피크를 가지며 천공과 공동의 제원에 따라 해당 흡음 피크주파수가 결정된다. 이 방법에 대한 타당성을 검증하기 위하여 유속에 따른 흡음 피크주파수의 변화를 실험결과⁽¹⁶⁾와 비교하였다. 실험결과와 비교하기 위한 이론 기반의 계산결과들은 모두 2절의 이론 바탕으로 도출되었다. Fig. 3은 식 (18)을 통해 도출된 유속 10 m/s, 30 m/s, 50 m/s, 100 m/s에서의 흡음 피크주파수에 대한 예측결과와 동일 조건에서의 실험결과를 나타낸다. 해당 결과들은 헬름홀츠 공진에 의한 흡음 피크주파수를 천공 직경과 유속으로 무차원화한 Strouhal 수로 표현되었다. 예측 및 실험결과 모두 유속이 증가함에 따라 흡음 피크주파수가 동일하게 감소하는 것을 확인하였다. 추가적인 검증을 위하여 유동환경에 의한 흡음 스펙트럼 결과를 도출하고 실험결과⁽¹⁷⁾와 비교하였다. Fig. 4는 유속 75 m/s에서의 탄성공명패널 흡음 스펙트럼에 대한 예측과 실험결과를 나타낸다. 예측과 실험결과에서 모두 헬름홀츠 공진에 의한 흡음 피크가 발생하였다. 해당 흡음 스펙트럼에서 탄성공명패널 고유모드에 의한 흡음 피크는 확인할 수 없었는데 이는 패널의 두께가 1 T로써 얇은 구조물에 해당함에 따라 구조 공진에 의한 고유모드가 관심주파수 범위 외에서 형성되어 나타나지 않은 것으로 판단된다. 예측 및 실험결과를 비교했을 때 전반적인 흡음률에 대한 경향과 흡음 공진에 의한 피크주파수에 대한 경향이 일치하였다. 해당 결과를 바탕으로 음향 임피던스 모델 기반의 유동환경을 반영한 탄성공명패널 흡음성능예측방법의 타당성을 입증하였다.

Fig. 3

Validation of Helmholtz peak frequency analysis results with experiments

Fig. 4

Validation of absroption coefficient spectrum analysis results at flow velocity 75 m/s

3.2 설계변수에 따른 탄성공명패널 흡음특성

목표 주파수의 소음을 저감시키기 위해서는 탄성공명패널의 흡음 피크주파수를 목표 소음저감 주파수에 일치하도록 탄성공명패널을 설계하는 것이 중요하다. 따라서 유동환경에 따른 탄성공명패널의 흡음 피크주파수의 변화 및 해당 흡음 피크주파수의 크기에 대한 분석을 수행하였다. 도출된 결과들은 3.1절에서 검증된 이론 기반의 흡음성능예측기법을 바탕으로 도출되었다. 분석에 사용된 패널의 제원 및 물성치는 Table 1과 동일하다.

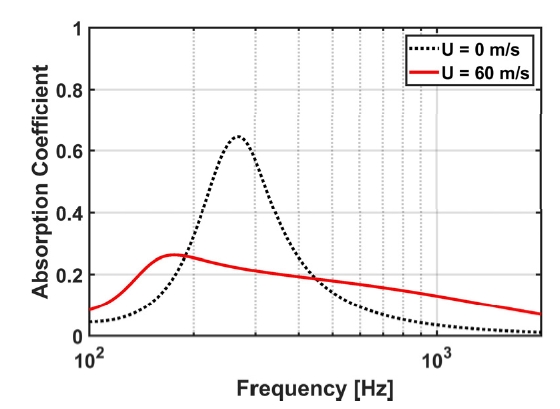
Fig. 5는 검증된 흡음성능예측이론을 바탕으로 도출된 유동의 유무에 따른 탄성공명패널의 흡음성능을 나타낸다. 검정색 점선과 빨간색 실선은 각각 유동이 없을 때와 60 m/s의 유동이 있을 때의 흡음성능을 나타낸다. 유동이 고려됨에 따라 피크 흡음률이 감소하였는데 이는 유동 영향으로부터 발생하는 흡음성능의 저하를 의미한다. 탄성공명패널은 패널의 천공과 공동 내 공기층 사이의 헬름홀츠 공진에 의한 흡음특성을 가진다. 해당 패널 주변에 유동이 흐르게 되면 천공과 공동 내부로 유동이 유입됨에 따라 헬름홀츠 공진이 구현되기 위한 주변 공기층이 유입류의 방해를 받게 된다. 주변 공기층이 방해를 받게 됨에 따라 유동이 흐르게 되면 유동이 흐르지 않을 때와 비교했을 때 흡음성능이 저하된다. 더하여, 흡음 피크주파수가 이동하는 것을 확인할 수 있는데 해당 흡음 피크주파수의 이동은 2.2절의 탄성공명패널 흡음성능예측이론에 식 (2)의 유동환경을 고려한 임피던스를 적용함으로써 유동영향이 반영됨에 따라 나타난 현상에 해당한다. 추가적으로 유동을 고려함에 따라 흡음률 분포 주파수 대역이 넓어짐을 확인할 수 있는데 이 영향은 유동이 고려됨에 따라 난류소산에 의한 흡음효과가 추가적으로 반영되어 나타난 것으로 판단된다. 유동환경이 고려됨에 따라 흡음 피크주파수 및 흡음 피크 크기가 변화하기 때문에 목표 주파수 대역의 소음 저감을 위한 탄성공명패널 설계를 수행하기 위해서는 해당 영향을 필수적으로 고려해야한다.

Fig. 5

Analysis results of absorption coefficient with and w/o flow

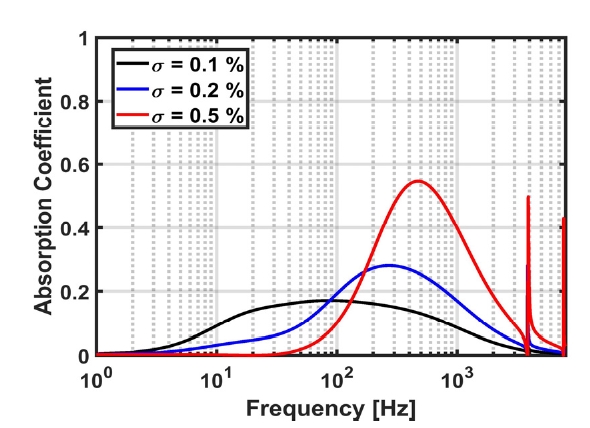
Fig. 6은 이론 기반으로 도출된 유속 50 m/s일 때 공극률 변화에 따른 탄성공명패널의 흡음성능을 나타낸다. 공극률이 증가함에 따라 흡음 피크주파수가 증가하고 전체적인 흡음률이 커졌다. 공극률이 증가하는 것은 헬름홀츠 공진 시스템에서의 면적이 증가하는 효과와 동일하기 때문에 공극률 증가에 따라 해당 흡음 피크주파수가 증가한다. 공극률이 작을 경우 유동영향에 의해 전체적인 흡음성능이 저하되기 때문에 탄성공명패널을 통한 소음을 저감시키기 위해서는 충분한 공극률을 가지는 탄성공명패널을 적용해야한다.

Fig. 6

Analysis results of absorption coefficient for perforation ratio at flow velocity 50 m/s

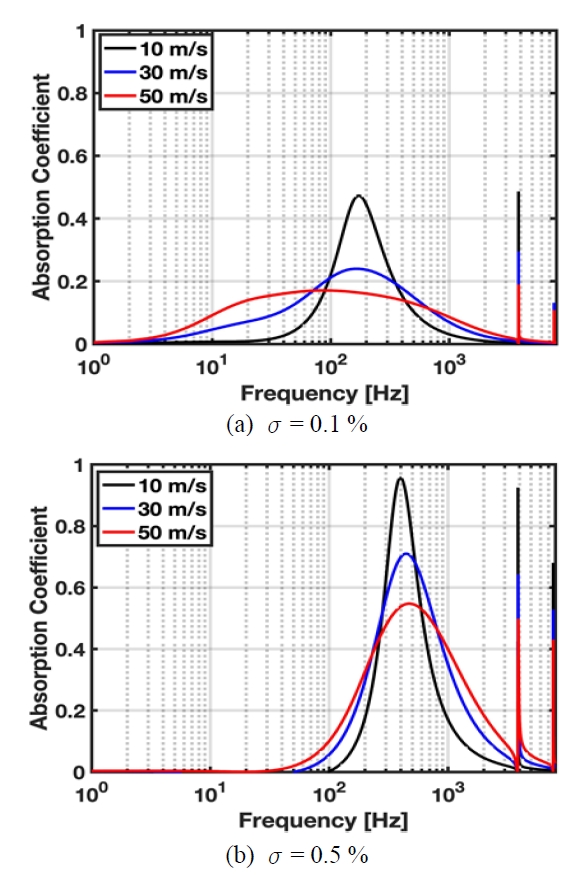
Fig. 7은 흡음성능예측이론을 기반으로 도출된 유속 별 미세천공판의 공극률에 따른 탄성공명패널의 흡음성능을 나타낸다. 각 공극률에 따른 탄성공명패널의 흡음성능을 분석했을 때 유속 증가에 따라 흡음률 크기가 모두 감소하는 것을 확인하였다. 유속이 증가함에 따라 유입류에 의한 천공 및 공동 주변 공기층의 방해 영향이 증가하기 때문에 유속 증가에 따라 흡음률이 전반적으로 낮아지게 된다.

Fig. 7

Analysis results of absorption coefficient for flow velocity

더하여, 흡음 피크주파수의 경우 공극률 증가에 따라 유속증가에 따른 흡음 피크주파수 이동 경향이 반전되는 것을 추가적으로 확인하였다. 유속 증가에 따른 흡음 피크주파수 이동 경향의 반전 현상은 헬름홀츠 공진에 의한 흡음 메커니즘과 주변 유동현상의 상관관계로부터 분석가능하다. 헬름홀츠 공진에 의한 흡음 메커니즘은 헬름홀츠 공진 질량-스프링 시스템으로부터 모사가능하다^(18~21). 공극률이 작을 경우 속도 증가에 따라 천공 주변에 발생하는 와류량이 감소하게 되며 상대적으로 헬름홀츠 공진 시스템에서의 질량 성분이 증가하는 효과를 발생시킨다. 해당 영향으로부터 유속 증가에 따라 흡음 피크주파수가 감소한다. 탄성공명패널 공극률이 클 경우 유속 증가에 따라 내부유입류량이 증가하기 때문에 헬름홀츠 공진 시스템에서의 스프링 성분이 증가하는 효과를 발생시키며 해당 영향으로부터 헬름홀츠 공진에 의한 흡음 피크주파수가 증가한다. Fig. 7에서의 공극률 0.1 % 경우는 공극률이 작음에 따라 헬름홀츠 공진 시스템에서의 질량 성분이 주도적으로 작용하였으며 이로부터 유속 증가에 의한 흡음 피크주파수가 감소하였다. 공극률 0.5 %의 경우는 공극률이 커짐에 따라 헬름홀츠 공진 시스템에서의 스프링 주도적으로 작용하게 되고 유속 증가에 의한 흡음 피크주파수가 증가하였다. Fig. 7의 결과와 같이 유속 증가에 따른 흡음 피크주파수 이동 경향이 공극률 별로 변화하기 때문에 탄성공명패널 설계를 수행할 때 해당 공극률의 영향을 반드시 고려해야한다.

Table 2와 Table 3은 각각 천공직경 0.5 mm, 1 mm일 때의 유속 별 공극률에 따른 탄성공명패널의 흡음 피크주파수를 나타낸다. 각 천공직경 별 유속증가에 따른 흡음 피크주파수의 증감 경향은 동일하게 나타나지만 증감경향이 변화하는 기준 공극률의 변화가 있음을 확인하였다. 천공직경 0.5 mm의 경우 공극률 0.2 % 일 때 유속 30 m/s에서 50 m/s로 증가함에 따라 흡음 피크주파수가 감소하였지만 천공직경 1 mm의 경우 동일한 흡음 피크주파수를 가지는 것을 확인하였다. 이에 따라 천공직경 1 mm의 경우 공극률 0.2 % 근처에서 유속에 따른 흡음 피크주파수 증감 경향이 변화하는 기준 공극률을 가짐을 확인할 수 있으며 천공직경 0.5 mm의 경우 0.2 %보다 높고 0.5 %보다 낮은 공극률에서 기준 공극률을 가짐을 확인하였다. 이 결과를 바탕으로 탄성공명패널의 설계변수에 따라 기준 공극률이 변화하기 때문에 정확한 기준 공극률을 도출한 후 해당 공극률을 바탕으로 소음저감 설계를 수행해야함을 해석적으로 확인하였다.

Table 2

Analysis results of Helmholtz resonance peak frequency for U and σ at hole diameter 0.5mm

Table 3

Analysis results of Helmholtz resonance peak frequency for U and σ at hole diameter 1mm

3.3 흡음특성 고려한 탄성공명패널 설계방안

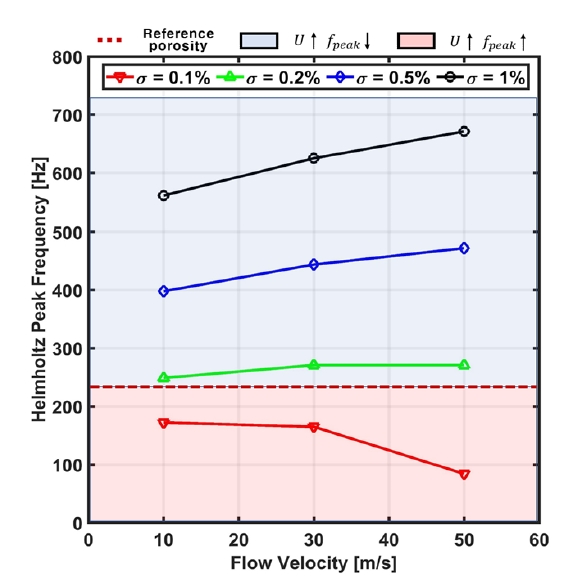
Fig. 8은 이론 기반으로 계산된 천공직경 1 mm일 때 공극률 별 유속에 따른 탄성공명패널의 흡음 피크주파수를 나타낸 그래프이다. 이 그래프에 따라 유속에 따른 흡음 피크주파수 증감 경향이 반전되는 기준 공극률이 0.2 % 근처에서 형성되는 것을 확인할 수 있다. 해당 기준 공극률에 따라 흡음 피크주파수 증감 경향이 반전되기 때문에 해당 기준 공극률을 설계 기준 공극률로 설정한 후 공극률의 구간을 구분하여 유동영향을 반영한 탄성공명패널의 설계를 수행해야한다. 현재 탄성공명패널의 경우 공극률 0.2 %보다 높은 공극률을 사용하게 되면 유동환경에 따라 흡음 피크주파수가 증가하기 때문에 철도소음 저감을 위한 저주파수 설계 관점에서 불리하다. 공극률이 0.2 %보다 낮은 경우 유동환경에 따라 흡음 피크주파수가 감소하기 때문에 저주파수 설계 관점에서 유리하지만 유속 증가에 따른 전체적인 흡음률 감소 경향은 동일하게 발생하기 때문에 충분한 흡음률을 갖기 위해서는 높은 공극률의 모델을 사용하는 것이 유리하다. 종합적으로 저주파수 대역의 철도소음을 저감시키 위해서는 공극률이 높은 탄성공명패널 모델을 바탕으로 설계 및 적용을 수행해야하며 공극률이 높은 모델의 경우 유속 증가에 따라 흡음 피크주파수가 증가하기 때문에 목표하는 소음저감 설계 주파수보다 낮은 주파수로 탄성공명패널 설계를 수행해야 원하는 주파수 대역의 소음을 저감시킬 수 있다.

Fig. 8

Analysis results of Helmholtz resonance peak frequency for U and σ at hole diameter 1 mm

4. 결 론

이 논문에서는 음향 임피던스 모델을 바탕으로 유동환경을 고려한 탄성공명패널에 대한 흡음성능예측기법을 정립하고 해당 방법으로 도출된 결과와 실험결과를 비교함으로써 이 방법의 타당성을 검증하였다.

검증된 방법을 바탕으로 패널 주변 유동 유무에 따른 탄성공명패널의 흡음특성을 분석하였으며 해당 결과를 통해 유동에 의한 흡음률의 감소 및 흡음 피크주파수의 이동 현상을 해석적으로 확인하였다. 더하여, 설계변수에 따른 탄성공명패널의 흡음성능을 도출하였으며 공극률에 따른 흡음 피크주파수를 헬름홀츠 공진 질량-스프링 시스템 관점으로 분석함으로써 흡음 피크주파수의 이동 및 이동 경향의 반전현상을 분석하였다. 흡음 피크주파수의 증감 경향이 특정 공극률을 기준으로 변화함에 따라 해당 특정 공극률을 설계 기준 공극률로 설정하였으며 해당 설계 기준 공극률을 바탕으로 저주파수 대역의 철도소음을 저감시킬 수 있는 설계 방안을 제시하였다.

향후에는 패널 주변에 접선유동이 형성됨에 따라 추가적으로 발생하는 난류경계층에 의한 공력 공진(aerodynamics coincidence)을 추가적으로 고려한 연구가 필요하다. 해당 공력 공진이 저주파수 대역에서 형성됨에 따라 해당 영향을 고려한 탄성공명패널의 설계기법을 구축한다면 저주파수 대역의 철도소음 저감에 더욱 기여가 가능할 것으로 기대된다.

Acknowledgments

이 연구는 서울대학교 BK21 해양플랜트 창의인재 양성사업단의 지원을 받아 수행하였습니다. 또한, 해양시스템공학연구소(RIMSE) 및 연구재단(2019R1F1A1062914)의 지원을 받아 수행하였습니다.

References

• Meissner, M., 2002, Excitation of Helmholtz Resonator by Grazing Air Flow, Journal of Sound and Vibration, Vol. 256, No. 2, pp. 382~388. [https://doi.org/10.1006/jsvi.2001.4219]
• Selamet, E., Selamet, A., Iqbal, A. and Kim, H., 2011, Effect of Flow on Helmholtz Resonator Acoustics: A Three-dimensional Computational Study vs. Experiments (No. 2011-01-1521), SAE Technical Paper. [https://doi.org/10.4271/2011-01-1521]
• Ghanadi, F., Arjomandi, M., Cazzolato, B. and Zander, A., 2014, Understanding of the Flow Behaviour on a Helmholtz Resonator Excited by Grazing Flow, International Journal of Computational Fluid Dynamics, Vol. 28, No. 5, pp. 219~231. [https://doi.org/10.1080/10618562.2014.922681]
• Maa, D. Y., 1975, Theory and Design of Microperforated Panel Sound-absorbing Constructions, Scientia Sinica, Vol. 18, No. 1, pp. 55~71.
• Maa, D. Y., 1998, Potential of Microperforated Panel Absorber, Journal of the Acoustical Society of America, Vol. 104, No. 5, pp. 2861~2866. [https://doi.org/10.1121/1.423870]
• Lee, J. and Swenson, G. W., 1992, Compact Sound Absorbers for Low Frequencies, Noise Control Engineering Journal, Vol. 38, No. 3, pp. 109~117. [https://doi.org/10.3397/1.2827811]
• Sakagami, K., Morimoto, M. and Koike, W., 2006, A Numerical Study of Double-leaf Microperforated Panel Absorbers, Applied Acoustics, Vol. 67, No. 7, pp. 609~619. [https://doi.org/10.1016/j.apacoust.2005.11.001]
• Toyoda, M. and Takahashi, D., 2008, Sound Transmission Through a Microperforated-panel Structure with Subdivided Air Cavities, Journal of the Acoustical Society of America, Vol. 124, No. 6, pp. 3594~3603. [https://doi.org/10.1121/1.3001711]
• Park, S. H. and Seo, S. H., 2011, Absorption Characteristics of Micro-perforated Panel Absorber According to High Incident Pressure Magnitude and Variation of Geometric Parameters, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 21, No. 11, pp. 1059~1066. [https://doi.org/10.5050/KSNVE.2011.21.11.1059]
• Bauer, A. B., 1977, Impedance Theory and Measurements on Porous Acoustic Liners, Journal of Aircraft, Vol. 14, No. 8, pp. 720~728. [https://doi.org/10.2514/3.58844]
• Allam, S., Guo, Y. and Åbom, M., 2009, Acoustical Study of Micro-perforated Plates for Vehicle Applications (No. 2009-01-2037), SAE Technical Paper. [https://doi.org/10.4271/2009-01-2037]
• Allam, S. and Åbom, M., 2008, Experimental Characterization of Acoustic Liners with Extended Reaction, In 14th AIAA/CEAS Aeroacoustics Conference (29th AIAA Aeroacoustics Conference), p. 3074. [https://doi.org/10.2514/6.2008-3074]
• Allam, S. and Åbom, M., 2011, A New Type of Muffler Based on Microperforated Tubes, Journal of Vibration and Acoustics, Vol. 133, No. 3, p. 031005. [https://doi.org/10.1115/1.4002956]
• Takahashi, D., 1990, Sound Transmission through Single Plates with Absorptive Facings: Improved Theory and Experiment, Journal of the Acoustical Society of America, Vol. 88, No. 2, pp. 879~882. [https://doi.org/10.1121/1.399738]
• Takahashi, D. and Tanaka, M., 2002, Flexural Vibration of Perforated Plates and Porous Elastic Materials under Acoustic Loading, Journal of the Acoustical Society of America, Vol. 112, No. 4, pp. 1456~1464. [https://doi.org/10.1121/1.1497624]
• Bravo, T., Maury, C. and Pinhede, C., 2017, Absorption and Transmission of Boundary Layer Noise through Flexible Multi-layer Micro-perforated Structures, Journal of Sound and Vibration, Vol. 395, pp. 201~223. [https://doi.org/10.1016/j.jsv.2017.02.018]
• Chang, D., Lu, F., Jin, W. and Liu, B., 2018, Low-frequency Sound Absorptive Properties of Double-layer Perforated Plate under Grazing Flow, Applied Acoustics, Vol. 130, pp. 115~123. [https://doi.org/10.1016/j.apacoust.2017.09.016]
• Meissner, M., 2002, Excitation of Helmholtz Resonator by Grazing Air Flow, Journal of Sound and Vibration, Vol. 256, No. 2, pp. 382~388. [https://doi.org/10.1006/jsvi.2001.4219]
• Sakagami, K., Morimoto, M. and Yairi, M., 2009, A Note on the Relationship between the Sound Absorption by Microperforated Panels and Panel/membrane-type Absorbers, Applied Acoustics, Vol. 70, No. 8, pp. 1131~1136. [https://doi.org/10.1016/j.apacoust.2009.03.003]
• Toyoda, M., Mu, R. L. and Takahashi, D., 2010, Relationship between Helmholtz-resonance Absorption and Panel-type Absorption in Finite Flexible Microperforated-panel Absorbers, Applied Acoustics, Vol. 71, No. 4, pp. 315~320. [https://doi.org/10.1016/j.apacoust.2009.10.007]
• Selamet, E., Selamet, A., Iqbal, A. and Kim, H., 2011, Effect of Flow on Helmholtz Resonator Acoustics: A Three-dimensional Computational Study vs. Experiments (No. 2011-01-1521), SAE Technical Paper. [https://doi.org/10.4271/2011-01-1521]