하이브리드 모델링 기법과 베이지안 최적화를 통한 엔진 마운트 응답개선

2.1 FBS 이론

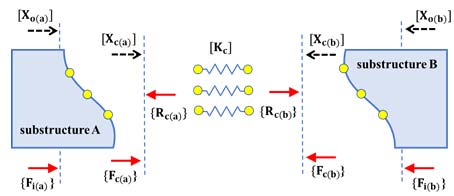
FBS 기법은 여러 개의 부분 구조물이 결합된 복잡한 시스템의 전달함수를 결합되는 지점에서의 displacement compatibility와 force equilibrium 성질을 이용해 부분구조물들의 전달함수로 표현하는 이론이다. 식 (1)은 두 개의 부분구조물 A, B가 결합되어 전체구조물을 이룰 때의 FBS 이론 식을 나타낸 것이며^(1~3), Fig. 1은 각 부분구조물 A, B가 결합되어 하나의 전체구조물을 이루는 모습을 보여준다.

Fig. 1

A two-substructure coupled system

여기서 [K_c]^-1항은 부분구조물 A와 B가 강체결합을 한다고 가정했을 때 0으로 수렴한다.

2.2 알터네이터의 ODS와 Waterfall 분석

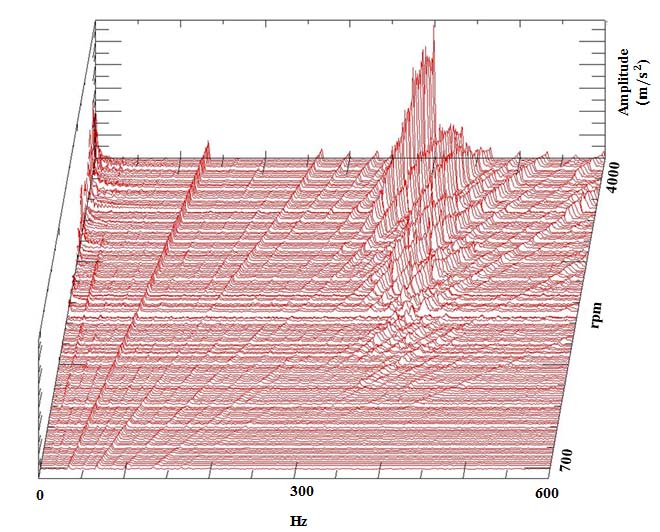
엔진을 이루는 여러 가지 부품 중 알터네이터의 경우 상대적으로 중량이 무거우며 엔진바디에 브라켓으로 연결되어있다. 따라서, 알터네이터에서 발생하는 진동은 엔진 마운트를 통해 결국 차량 바디로 전달된다. 즉, 알터네이터의 진동으로 인한 엔진 마운트의 응답을 줄이면 차량 바디로 전달되는 진동을 줄일 수 있다. 이 논문에서는 알터네이터의 진동 특성과 관심주파수대역 설정을 위해 엔진의 operational deflection shape (ODS) 분석을 진행하였다⁽⁴⁾. 엔진 RPM을 700부터 4000까지 증가시킨 결과를 기반으로 알터네이터의 진동 크기를 확인하였으며 이러한 분석을 통해 400 Hz 부근 대역에서 알터네이터의 Z축 방향 움직임이 큰 것을 확인하였다. Fig. 2는 알터네이터의 operational analysis를 토대로 얻어진 waterfall 결과이다. ODS와 waterfall 분석을 통해 하이브리드 모델링 기법 적용 시 개선시켜야 할 엔진 마운트의 관심 주파수대역을 350 Hz ~ 500 Hz로 설정하였으며, Z축 방향의 움직임을 줄이기 위해 알터네이터 브라켓의 Z축 방향 구조강성을 증가시키기로 결정하였다. 알터네이터 브라켓의 경우 cantilever beam의 형상을 띄기 때문에 굽힘에 대한 저항력을 증가시켜 그 움직임을 억제할 수 있다.

Fig. 2

Waterfall result of alternator in Z-direction

2.3 하이브리드 모델링 기법의 신뢰성 판단

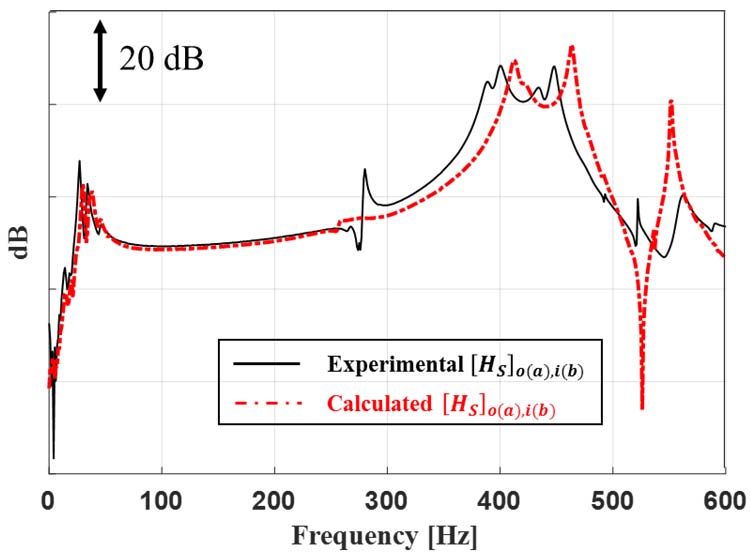
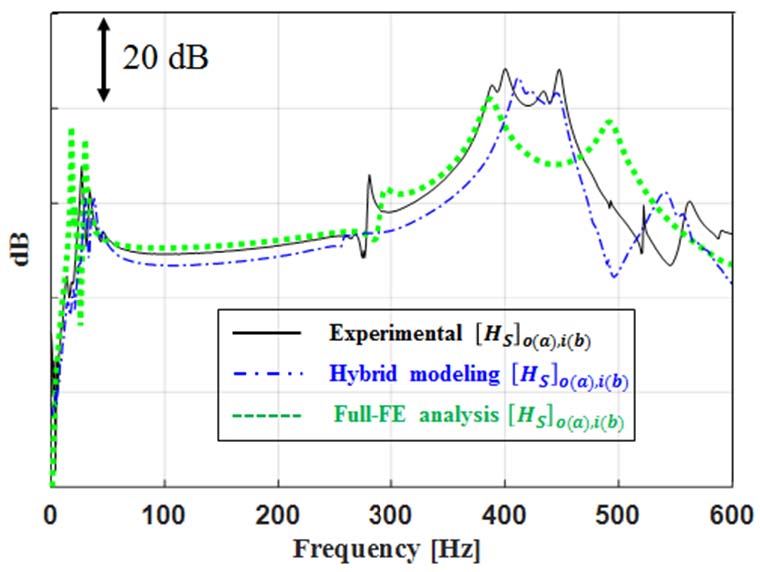
하이브리드 모델링 기법을 적용하기 전에 부분구조물의 전달함수로 계산된 전체구조물의 전달함수가 실제 전달함수를 적절하게 예측하는지와 Fig. 1에서 부분구조물 B를 FE 결과로 대체하였을 때 얻어진 하이브리드 모델링의 결과가 full-FE 해석으로만 분석하였을 때 얻어진 결과에 비해 개선되었는지 확인이 필요하다. 부분구조물 A의 경우 엔진바디와 마운트가 포함된 구조물이며, 부분구조물 B의 경우 알터네이터와 알터네이터 브라켓이 포함된 구조물을 의미한다. Fig. 3은 부분구조물의 시험 결과를 이용해 계산된 전체시스템의 전달함수와 전체구조물을 실제 측정한 결과를 비교한 것이다. Fig. 3을 보면 관심 주파수대역인 350 Hz ~ 500 Hz에서 예측한 전달함수 레벨과 피크가 유사하며 이를 통해 하이브리드 모델링 기법에 이용되는 식 (1)의 유효성을 확인 할 수 있다. 식 (1)의 유효성을 확인하였으면 부분구조물의 시험 값을 FE 해석 결과로 대체하여 하이브리드 모델링 기법으로 예측한 결과의 신뢰성을 파악하여야 한다. Fig. 4는 실제 측정결과, full-FE 해석결과, 하이브리드 모델링 기법으로 얻어진 [H_S]_o(a),i(b)를 비교한 것이다. 이를 통해, 하이브리드 모델링 기법 적용 시 full-FE 해석으로 얻은 [H_S]_o(a),i(b)에 비해 실제 측정결과를 더 잘 묘사한다. 이는 하이브리드 모델링의 경우 전체구조물의 전달함수를 계산할 때 실제 측정값이 사용되기 때문이다. Table 1을 보면 full-FE 해석과 하이브리드 모델링 기법 적용 시 소요되는 시간을 비교하였다. Full-FE 해석은 [H_S]_o(a),i(b)를 얻기 위해 총 11시간이 소요되나 하이브리드 모델링 기법을 이용할 경우 이의 0.76 %에 해당하는 5분 정도가 소요된다. 전체구조물의 전달함수를 예측하는데 짧은 시간이 소요된다는 장점은 부분적으로 FE 해석이 적용된 부분구조물의 설계변경에 대한 다양한 사례 연구를 할 수 있다. 이는 실제 물리적 모델 없이 많은 경우에 대해 [H_S]_o(a),i(b)를 예측 할 수 있으며 3장에 소개될 베이지안 최적화를 적용하여 알터네이터 브라켓의 구조강성 변경을 최적화 시키기 위한 초석이 된다.

Fig. 3

Comparison of experimental and calculated [HS]o(a),i(b)in Z-direction

Fig. 4

Comparison of experimental, hybrid modeling and full-FE analysis [HS]o(a),i(b)in Z-direction

Table 1

Comparison of the time required to calculate [HS]o(a),i(b)

2.4 하이브리드 모델링 기법 적용

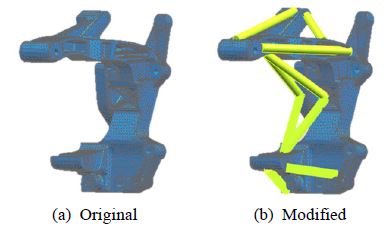
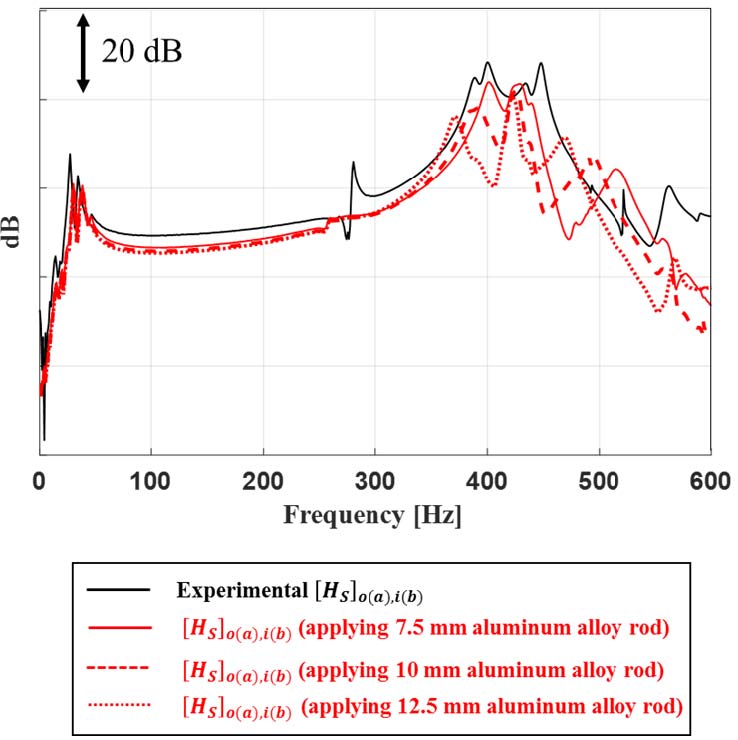
앞서 하이브리드 모델링 기법의 유용성을 확인하였으므로 FE 해석이 적용된 부분구조물 B에서 알터네이터 브라켓의 구조강성을 변경하여 전체구조물의 진동 응답 레벨이 어떻게 변하는지 예측하였다. 구조강성 변경 대상은 알터네이터 브라켓이며 ODS분석을 통해 400 Hz 대역 부근에서 Z축 방향의 움직임이 큰 것을 확인하였으므로 Z축 방향의 움직임을 억제하기 위해 가상의 rod를 덧대었다. Fig. 5는 기존 브라켓과 구조강성 변경한 브라켓을 나타낸 것이다. Rod는 총 9개가 사용되었으며 모두 Z축 방향의 움직임 억제를 고려하여 위치를 설정하였고, 지름은 7.5 mm, 10 mm, 12.5 mm, 재질은 기존 브라켓과 동일한 aluminum alloy 그리고 steel인 경우에 대해 분석하였다. Table 2는 각 재질의 물성치를 나타낸 것이다. Table 3는 aluminum alloy rod를 사용하였을 때 각 rod의 지름에 대해 관심 주파수 대역에서 전체 응답레벨 변화와 기존 브라켓에서의 전체 응답레벨을 비교한 것이며, Fig. 6은 aluminum alloy rod의 두께 변화에 따라 전체구조물의 [H_S]_o(a),i(b)를 예측한 것이다.

Fig. 5

Alternator bracket

Table 2

Material property of aluminum and steel

Table 3

Comparison of overall response level (applying aluminum alloy rod, 350 Hz to 450 Hz)

Fig. 6

Comparison of [HS]o(a),i(b)in Z-direction according the diameter of aluminum alloy rod

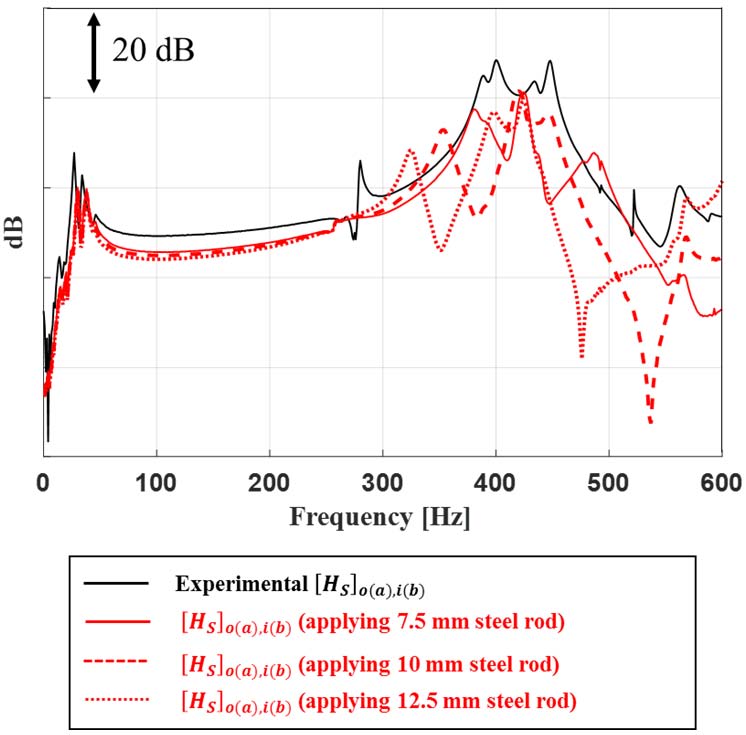
Table 4는 동일한 두께 조건으로 steel rod를사용하였을 때 전체 응답레벨을 비교한 것이며, Fig. 7은 steel rod의 두께 변화에 따라 전체구조물의 [H_S]_o(a),i(b)를 예측한 것이다. 이를 통해 브라켓 구조강성 변경 시 엔진 마운트의 응답 레벨을 개선 시킬 수 있음을 확인하였다.

Table 4

Comparison of overall response level (applying steel rod, 350 Hz to 450 Hz)

Fig. 7

Comparison of [HS]o(a),i(b)in Z-direction according the diameter of steel rod

3.1 베이지안 최적화 이론

베이지안 최적화는 지능적 샘플링 과정을 통해 주어진 모델의 최적 파라미터를 탐색하는 알고리즘이다. 특히 목적함수를 모르거나 수학적으로 표현하기 어려운 black-box optimization 문제를 효율적으로 해결할 수 있으며, 최근 기계학습, 딥러닝 등 인공지능 알고리듬의 hyperparameter를 효과적으로 튜닝할 수 있어 크게 각광받고 있다⁽⁵⁾. 베이지안 최적화의 핵심 아이디어는 최소한의 탐색으로 최적값을 찾는 것이다. 이를 위해 현재까지 관측된 정보를 기반으로 미지의 목적함수를 확률적으로 추정하는 surrogate model을 이용한다. 이 연구에서는 식 (3)과 같이 베이지안 선형 회귀 모델을 이용하였다.

여기서 x∈R^d는 input 벡터, ϕ:R^d→R^l는 feature map, w∈R^l은 weight 벡터, ϵ은 N(0,σ²)을 따르는 노이즈이다. 이 연구에서는 식 (4)와 같이 feature map의 inner product가 width가 η인 가우시안 커널에 해당하도록 정의하였다⁽⁶⁾.

학습된 surrogate model로부터 빠르게 최적점을 탐색하기 위해서는 최적점이 존재할 가능성이 높은 위치를 탐색하는 함수가 필요하며, 이는 acquisition function으로 정의된다. 이 연구에서는 가장 널리 사용되는 expected improvement(EI) 함수를 이용하였고 이는 식 (5)와 같이 정의된다⁽⁷⁾.

여기서 f(x⁺)는 현재까지 조사한 관측값 중 최대 함수값을 의미한다. EI를 이용한 acquisition function은 현재까지 탐색된 데이터를 기반으로 최적 포인트가 존재할 가능성이 높은 위치를 추정하며, 해당 포인트의 관측을 통해 surrogate model이 갱신된다. 이러한 반복적 학습의 과정을 거쳐 효과적으로 global optimum값을 찾아낼 수 있다.

3.2 베이지안 최적화를 이용한 알터네이터 브라켓 구조강성 최적화

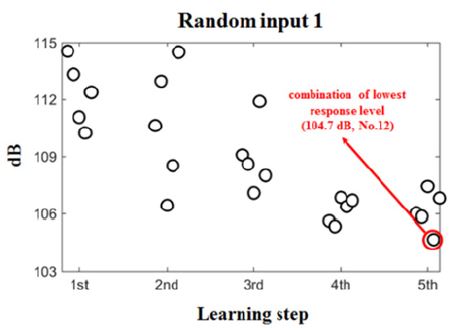
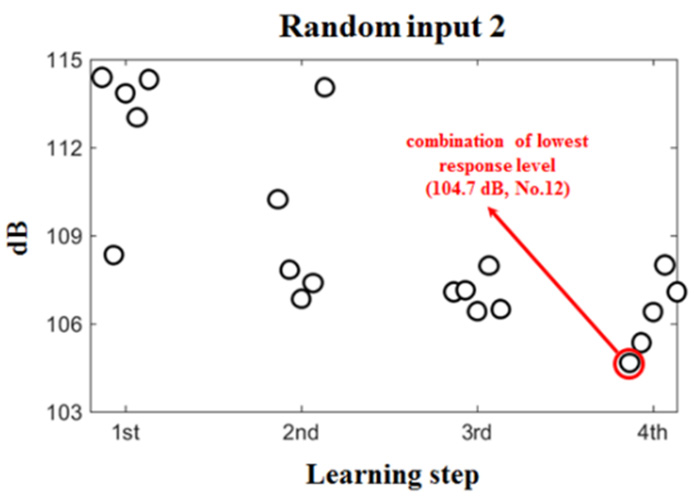
앞서 9개의 rod를 이용해 브라켓의 구조강성을 변경할 경우 중량이나 비용적인 측면에서 다소 불리하다. 따라서, 적은 rod의 개수로도 효율적인 엔진 마운트 응답 저감을 위해 베이지안 최적화 기법을 활용하였다. 9개의 rod 중 임의의 4개 rod를 선정한다고 가정하면 126개의 독립적인 경우를 가지는 조합이 나온다. 이 논문에선 각 조합을 구분하기 위해 임의로 No. 1 ~ No. 126까지의 번호를 부여하였다. 이 경우의 수를 모두 시행하기엔 소요시간이 지나치게 많이 필요하기 때문에 베이지안 최적화를 활용해 최소의 조합만을 검증하여 최적의 조합을 찾아내었다. 최초 임의의 5개 조합을 input으로 하여 surrogate model을 학습한 뒤 acquisition function을 통해 다음 5개 조합을 추천받는다. 추천받은 5개 조합의 응답레벨을 다시 input으로 하여 같은 학습과정을 반복한다. Fig. 8은 최초 설정한 임의의 5개 조합(random input 1)에 대해서 5번의 학습을 통해 가장 낮은 응답 레벨을 갖는 조합을 확인한 것이며 필요한 검증 데이터의 수는 126개 중 약 20 % 정도인 25개의 데이터에 불과하다. Fig. 9은 input으로 사용될 임의의 조합을 다르게 설정하여(random input 2) 학습을 진행한 결과이다. Random input 1과 비교하였을 때 전체 조합수의 약 16 % 수준인 20개 조합의 검증만으로도 최적의 조합을 찾을 수 있었다. 104.7 dB를 가지는 최적의 조합 No. 12의 검증을 위해 126개의 조합을 모두 하이브리드 모델링 기법을 통해 확인하였고, 그 결과 가장 낮은 응답레벨을 갖는 최적의 조합임을 확인 할 수 있었다. Fig. 10은 최적의 조합인 No. 12의 rod 위치를 묘사한 것이다.

Fig. 8

Learning steps to find the optimal combination (using first random input)

Fig. 9

Learning steps to find the optimal combination (using second random input)

Fig. 10

Optimal modified bracket (No.12)