[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 30, No. 6, pp.608-614

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Dec 2020

Received 21 Sep 2020 Revised 16 Oct 2020 Accepted 20 Oct 2020

DOI: https://doi.org/10.5050/KSNVE.2020.30.6.608

철로의 파동 전파특성 분석을 통한 무한 레일의 등가 동적물성 예측

김걸^* ; 박준홍^†

Prediction of the Equivalent Dynamic Properties of Infinite Rail with Wave Propagation Analysis on the Railway Track

Jie Jin^* ; Junhong Park^†

*Department of Mechanical Engineering, Hanyang University, Student

Correspondence to: ^†Member, Department of Mechanical Engineering, Hanyang University, Professor E-mail: parkj@hanyang.ac.kr ‡ Recommended by Editor Chan Jung Kim

Abstract

In this study, an experimental method is proposed to measure rail properties in discretely supported tracks. The variations in the dynamic characteristics of the rail pad according to the excitation were estimated. To simulate the equivalent stiffness of the fastening system due to the single fast clip (SFC) device and the rail pad, a modeling of the clamping system was proposed. The discretely supported track was analyzed using the transfer function method. The vibration responses of the track were analyzed to determine the transfer function. As the length of the track increases, the influence of the reflected wave from the joints decreases, and the traveling wave effect becomes dominant. The characteristics of the infinite track were observed. A model with 36.5 m (50 sleepers) railway track was applied to predict the equivalent properties of the rail on discrete supports for each frequency using Newton-raphson method.

Keywords:

Rail Pad, Dynamic Property, Railway Track, Wave Propagation

키워드:

레일 패드, 동적물성, 레일 궤도, 파동 전파

1. 서 론

열차 하중으로 인한 철로의 거동을 해석하고, 철로 진동으로 인한 방사 소음을 예측하기 위하여 다양한 철로 모델이 제안되었다. 레일 패드, 침목 및 도상이 연속적으로 레일을 지지하는 two-layer 지지 모델⁽¹⁾과 레일과 콘크리트 슬라브 사이에 레일 패드 요소만 고려하는 one-layer 지지 모델이 제안되어 왔다⁽²⁾. 레일 궤도가 무한하게 길다고 가정을 하였을 때, 연속 지지 모델을 이용한 파동 특성 분석이 가능하다. 그러나 길이가 유한한 레일 슬라브 궤도는 레일과 콘크리트 슬라브 사이에 레일 패드로 일정한 간격을 두고 지지하는 이산 지지 구조이다^(3,4). 따라서 이산 지지 철로의 파동 전파 특성을 고려한 무한 레일 모델링이 필요로 하고 있다. 또한 이산 지지된 철로 진동 특성을 정확하게 분석하기 위하여 레일 패드와 레일 등가 동적 물성 예측에 대한 연구가 필요하다.

레일 패드의 강성 측정방법으로는 유럽 표준 EN 13146-9과 이에 부합되는 한국 철도 표준 KRS TR 0014 규격이 있다. 레일 패드를 시험체에 설치 후 하중 재하 및 하중 제거에 의한 변위값을 이용하여 레일 패드의 정적 수직강성을 측정하는 방법이다⁽⁵⁾. 철도 차량 운행 시 발생되는 여러 가지 소음 중 전동소음(rolling noise)은 차륜과 레일표면의 불균일에 의해 가진된 레일의 진동에 기인된 소음이다. 전동소음에 대한 레일 패드의 영향은 궤도 종류에 따라 차이가 있지만 약 100 Hz ~ 400 Hz에서 영향이 지배적이다. 따라서 이 대역에서의 레일 패드의 동적 수직강성 및 궤도 레일의 동적 물성 값을 예측하기 위한 연구가 필요하다. 전달함수법은 복합 구조물의 동적 물성을 측정하기 위한 실험방법으로 콘크리트 구조물 및 제진재의 동적 물성 측정하는데 제안되었다^(6-8). 전동소음의 관점에서 국내 철도의 진동 특성 분석을 위하여 KRS50, KTX 궤도의 물성 값들을 비교하였고 이를 이용한 분산 선도 및 track decay rate을 계산하였다⁽⁹⁾.

이 연구에서는 이산 지지된 철로에서의 레일 등가 물성을 측정하기 위하여 하중에 따른 레일 패드의 물성을 측정하였고, 이를 통해 레일 패드에 하중이 인가되었을 때 발생하는 강성과 감쇠 인자 변화를 살펴보았다. 또한 전달함수법을 이용하여 이산 지지 궤도 모델링을 구축하였고 길이에 따른 철로의 파동 전파 특성을 분석하였다. 제시한 철로의 파동 특성 분석 모델을 통하여 무한 궤도 레일의 등가 동적 물성을 예측하였고, KRS50 레일 물성값과의 비교를 통하여 모델링을 검증하였다.

2. 하중에 따른 레일 패드의 물성 변화 고찰

2.1 실험 세팅

레일 패드(rail pad)는 레일과 콘크리트 침목 사이를 잇는 체결 장치에 들어가는 부품의 하나로 열차가 지나갈 때 생기는 진동을 흡수해 침목을 보호하는 절연 역할을 하는 고무 합성물이다. 고무합성물로 제작된 레일 패드는 레일 하중에 따라서 부드럽게 되거나 딱딱하게 변화하면서 진동 물성 특성의 차이가 발생하게 된다. 하중에 따른 패드 물성 변화 특성을 고찰하고, 실제 궤도에서의 패드 물성을 예측하기 위하여 Fig. 1과 같이 실험을 세팅하였다. 사이즈가 25 × 25 × 610 mm인 알루미늄 보의 한쪽 끝단을 유압 바이스(EHV-150)에 고정하여 고정-자유(fix-free)단 조건을 만족하였고, 중간 지점에 특수 제작한 지그(jig)를 세팅하였다. 지그에는 하중을 측정하기 위한 로드셸(KMR, 20 kN)을 고정하였다고 알루미늄 보와 지그 사이에 레일 패드 샘플을 고정하였다. 이때 지그 두 끝단에 장착된 너트의 체결을 통하여 레일 패드 샘플에 하중을 인가할 수 있다. 보의 고정단에서 각각 x₁ = 0.5 m, x₂= 0.47 m 떨어진 지점에 가속도계(PCB, model 352A21)를 설치하였고, 자유단을 가진하여 하중 변화에 따른 알루미늄 보의 진동에 대한 전달함수를 측정하였다.

Fig. 1

Experimental setup to measure dynamic characteristics of rail pad depending on different pressure

2.2 파동 특성 분석 모델 구성

Fig. 2는 이론 전달함수를 계산하기 위한 파동 해석 개략도를 표현하였다. 레일 패드 샘플로 인한 오일러(Euler) 보의 굽힘 진동 운동방정식은 식 (1)과 같다.

∑ k = 1 N E I ∂ 4 w k ξ k, t ∂ ξ k 4 + ρ A ∂ 2 w k ξ k, t ∂ t 2 = 0

(1)

Fig. 2

Schematic diagram to predict the transfer function with wave propagation method

여기서 E, I, ρ, A는 각각 알루미늄 보의 영률, 면적 관성 모멘트, 보의 밀도 및 단면적을 가리킨다. w_k는 변위, 하첨자 “k”는 레일 패드 샘플로 나뉜 좌우측 빔을 가리키며 이 연구에서는 N = 2로 해석 모델을 구성한다. 이때 알루미늄 보의 진동 응답을 구하기 위한 일반해는 식 (2)로 구해진다.

w^k (ξ k) = A^k, 1 sin ⁡ k b ξ k + A^k, 2 cos ⁡ k b ξ k + A^k, 3 e k b (ξ k - L k) + A^k, 4 e - k b ξ k

(2)

여기서 k_b, L₁, L₂는 각각 파수, 패드 샘플을 기준으로 하는 좌우 오일러 보의 길이를 가리킨다. 외팔보 경계조건과 레일 패드 장착위치에서의 진동 연속조건을 통하여 일반해 및 전달함수를 계산한다.

w^1 (0) = 0, ∂ w^1 (0) ∂ ξ 1 = 0, w^1 (L 1) = w^2 (0), ∂ w^1 (L 1) ∂ ξ 1 = ∂ w^2 (0) ∂ ξ 2, ∂ 2 w^1 (L 1) ∂ ξ 12 = ∂ 2 w^2 (0) ∂ ξ 22, ∂ 3 w^1 (L 1) ∂ ξ 1 3 - ∂ 3 w^2 (0) ∂ ξ 2 3 = k p E I w^2 0 ∂ 2 w^2 (L 2) ∂ ξ 22 = 0, ∂ 3 w^2 (L 2) ∂ ξ 23 = F e E I

(3)

여기서 k_p, F_e는 각각 레일 패드 강성 및 가진력을 가리킨다. 파동 특성 분석 모델을 이용하여 예측한 전달함수와 실험 측정한 전달함수의 비교를 통하여 알루미늄 보와 레일 패드의 물성을 Newton-raphson 수치해석법으로 계산 가능하다⁽⁶⁾.

2.3 하중에 따른 레일 패드 물성 변화 고찰

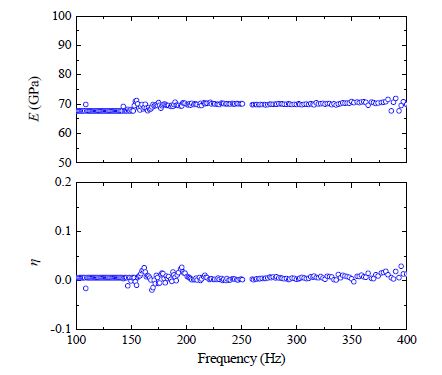
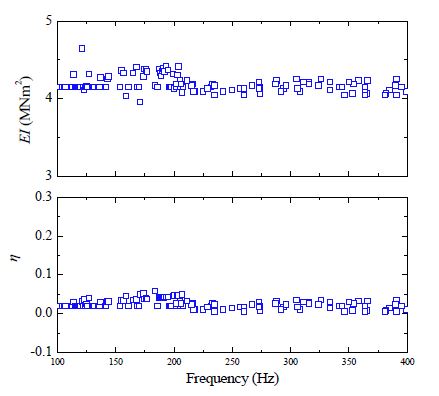
하중에 따른 레일 패드의 강성 값을 도출하기 위하여 먼저 실험에 사용되는 알루미늄 보의 물성이 필요하다. 알루미늄 보의 영률은 E = E × (1 + η)로 표기하여 진동 감쇠 크기는 손실 계수 η로 나타낸다. 손실 계수는 영률의 실수부에 대한 허수부의 비율로 계산된다. Fig. 3은 주파수에 따른 알루미늄 보의 동적 물성 예측 결과이다. 100 Hz ~ 400 Hz대역에서의 평균값을 계산해본 결과 알루미늄 보의 영률을 E = 70 × (1 + 0.006i) GPa 계산할 수 있다.

Fig. 3

The estimated spectral dynamic properties of aluminum beam with Newton-raphson method

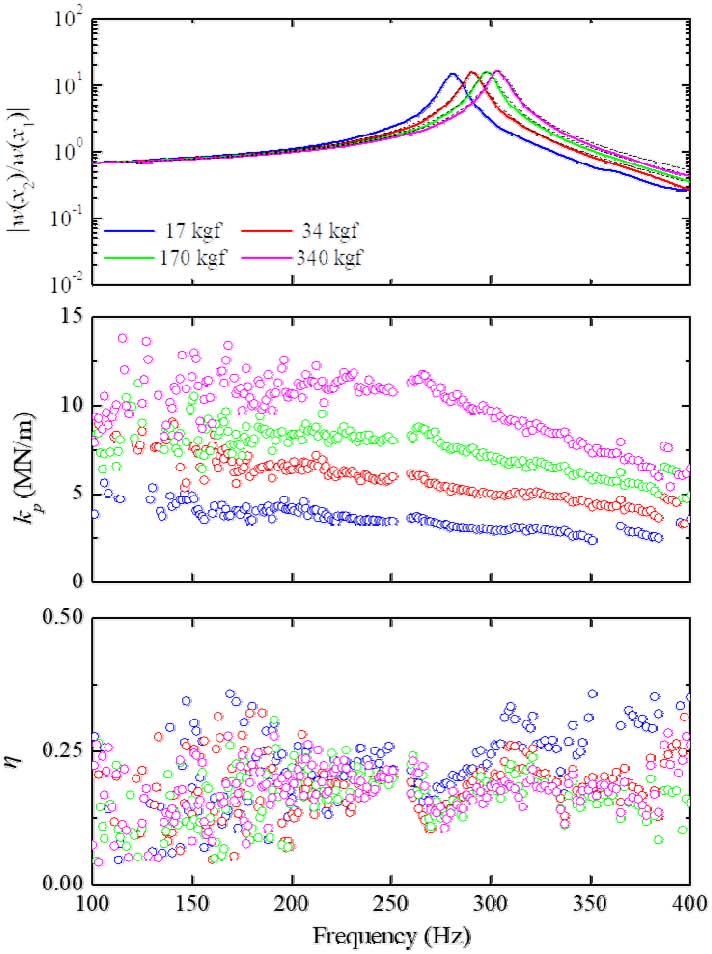
알루미늄 보의 기계적 물성을 E = 70 × (1 + 0.006i) GPa, I = 3.2552 × 10^-8m⁴, ρ = 1.7957 kg/m, A = 6.25 × 10^-4m², L₁= 0.10 m, L₂= 0.51 m으로 설정하였다. Fig. 4는 레일 패드에 각각 18.25 kgf, 36.5 kgf, 182.5 kgf, 365 kgf의 하중을 인가하였을 때의 전달함수 변화를 보여준다. 합성고무 재질의 레일 패드는 점탄성 성질을 소유하고 있음으로 강성을 k_p= k_p× (1 + η)로 표기할 수 있다. 이때 전달함수법을 이용하여 강성과 손실 계수를 예측할 수 있다. Fig. 4에서 실선은 실험 측정 전달함수, 점선은 패드 강성에 따른 예상 전달함수이다. 이때 전달함수의 모드 주파수는 인가되는 하중의 증가하면서 고주파수 대역으로 이동하는데, 이것은 레일 패드의 하중이 증가하면서 패드의 강성이 높아지기 때문이다. 레일의 진동 및 열차 소음 저감에 대한 레일 패드의 기여도는 저주파수 대역에서 크게 나타남으로 100 Hz ~ 400 Hz 대역을 목표로 비교하였다. 이때 하중 증가에 따른 패드 강성의 변화는 명확하고, 주파수 대역에서도 일정한 경향성으로 나타난다. 손실 계수는 주파수에 따른 경향성을 관찰하기는 어렵지만 하중 별 표준편차는 각각 0.071, 0.060, 0.058, 0.062으로 비슷한 수준으로 확인되었다.

Fig. 4

Variation of the dynamic properties of rail pad with different compressive forces

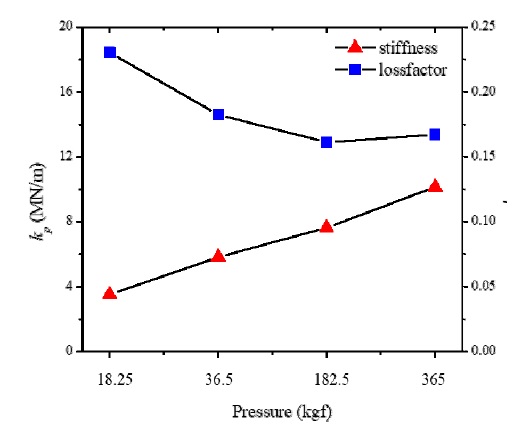
하중에 따른 패드 강성 및 손실 계수의 변화를 고찰하고, 해석 모델에 적용하기 위한 패드의 등가 물성을 도출하기 위하여 100 Hz ~ 400 Hz 대역의 물성 값들을 평균하여 Fig. 5와 같이 비교하였다. 패드에 인가되는 하중이 증가함에 따라 패드 동적 강성은 증가하고 손실 계수는 오히려 감소하다가 일정 값으로 수렴한다. 이것은 합성 고무 재질의 패드가 하중으로 밀착되기 때문이다. 제안한 방법을 통하여 실제 궤도의 무계 하중 별로 적용되는 레일 패드의 등가 동적 물성을 도출할 수 있다. KRS50 레일 궤도의 단위 경간(span)만큼의 무게에 해당되는 하중을 적용할 때, 레일 패드의 동적 강성은 k_p= 5.83 × (1 + 0.179i) MN/m으로 도출되었다.

Fig. 5

Variation in averaged stiffness and loss factor of different compressive forces on the rail pad in the frequency range from 100 Hz to 400 Hz

3. 이산 지지(discrete supports) 궤도에서의 레일 등가 물성 측정

3.1 슬라브 궤도의 침목 등가 강성

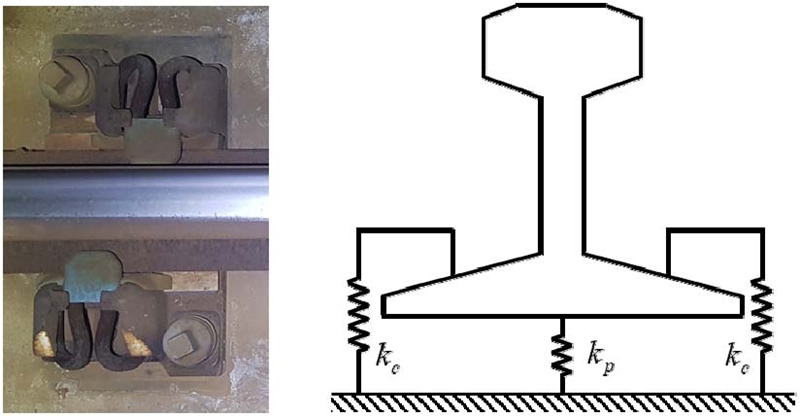
이산 지지된 궤도에서의 레일의 등가 동적 물성을 예측하기 위하여 인천 왕길-검단오류역의 상행선 궤도에서 실험을 진행하였다. 이 구간은 KRS50 레일을 사용되었고, 두개의 SFC(pandrol)형 체결 장치를 이용하여 레일 패드와 함께 콘크리트 슬라브에 고정하였다. Fig. 6은 SFC장치와 레일 패드 효과로 인한 체결 시스템의 등가 강성 모델로서 레일은 클립 강성과 패드 강성으로 병렬로 연결이 되었다. 체결 시스템의 등가 강성은

k e = k p + 2 k c

(4)

Fig. 6

Equivalent stiffness model of fastening system due to fastening device and rail pad effect

여기서 k_p, k_c는 각각 레일 패드 강성 및 SFC 장치 강성을 가리킨다. 이 값을 이산 지지 궤도 모델에 적용하여 궤도에서의 레일 등가 물성을 계산할 수 있다.

3.2 실험 세팅 및 수치 해석 모델

이산 지지 궤도에서의 레일의 등가 물성을 예측하기 위하여 실험 전달함수 측정 실험을 진행하였다. 이때 궤도의 이음매(joint)에서 발생하는 반사파의 영향을 최소화 하기 위하여, 이음매에서 12 m 떨어진 경간에서 실험을 진행하였다. Fig. 7은 클램핑 시스템의 등가 강성을 이용한 이산 지지된 레일 빔의 동적 물성 예측을 위한 실험 세팅 및 모델링이다. SFC 장치로 인한 열차 궤도의 1차 pinned-pinned모드를 유리하게 측정하기 위하여 클램핑 지점을 랜덤으로 가진하고, 가속도계(PCB, model 352A21)는 각각 응답이 가장 크게 발생하는 레일 경간(L₂= 0.335 m) 지점과 고정 모드 특성들이 안정적으로 발생하는 지점(L₁= 0.1675 m)에 세팅하고 진동응답에 대한 전달함수를 측정하였다. 이론 전달함수 계산하기 위하여 식 (1)을 이용하여 이산 지지된 레일을 모사한다. 이때 열차 레일의 영률, 면적 관성 모멘트, 보의 밀도 및 단면적을 적용한다. 궤도 이음매를 모사하기 위하여 고정-고정(fix-fix) 경계조건으로 하였다.

w^1 0 = 0, ∂ w^1 0 ∂ ξ 1 = 0, w^N L = 0, ∂ w^N L ∂ ξ N = 0

(6)

Fig. 7

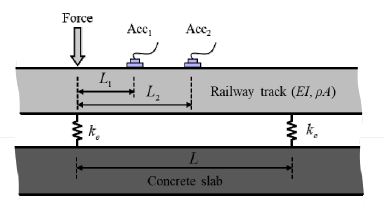
Schematic for predicting the dynamic properties of rail beam with discrete supports by the rail pad properties application

여기서 L, N은 클램핑 시스템의 경간 거리 및 수량을 가리킨다. 따라서 이론 궤도 모델의 길이는 L(N + 1) 미터로 계산할 수 있다. 이산 지지 레일의 반복 구조 특성을 모사하기 위하여 클램핑 시스템에서의 연속조건은 식 (7)과 같다.

∑ k = 1 N w^k (L) = w^k + 1 (0), ∑ k = 1 N ∂ w^k ∂ ξ k (L) = ∂ w^k + 1 ∂ ξ k + 1 (0), ∑ k = 1 N ∂ 2 w^k (L) ∂ ξ k 2 = ∂ 2 w^k + 1 (0) ∂ ξ k + 1 2, ∑ k = 1 N ∂ 3 w^k (L) ∂ ξ k 3 - ∂ 3 w^k + 1 (0) ∂ ξ k + 1 3 = k e E I w^k (L),

(7)

여기서 k_e는 클램핑 시스템의 등가 강성을 가리킨다. 이 연구에서는 궤도의 길이와 클램핑 시스템의 수량에 따른 진동 특성을 고찰하였고, 실제 궤도에서 측정 결과와 비교하였다.

3.3 궤도 길이에 따른 전달함수 비교

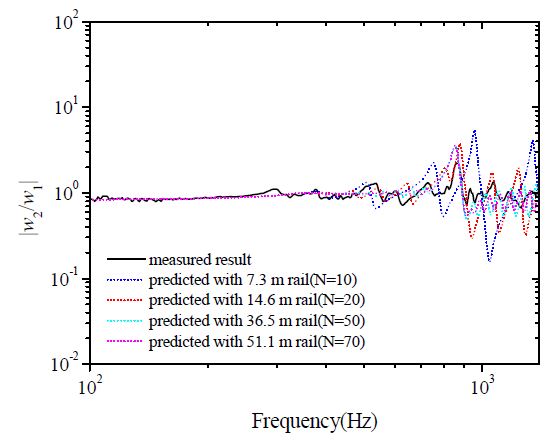
이산 지지된 궤도에서의 레일 등가 물성 예측을 위해서는 실험 및 이론 전달함수의 비교를 필요로 하다. 레일의 기계적 물성은 KRS50 레일로, 침목 경간의 길이 L = 0.73 m, SFC 강성은 pandrol 제품의 스팩 강성 k_c= 70 MN/m으로 하였다. Fig. 8은 길이가 각각 7.3 m, 14.6 m, 36.5 m, 51.1 m인 궤도 모델의 예측 전달함수와 실험 전달함수를 비교한 결과이다.

Fig. 8

Comparison of the measured and predicted transfer functions with rail beam length

궤도의 길이가 짧으면 이음매에서 발생하는 반사파의 영향을 지배적으로 나타나면서 모델은 유한 보의 특성들이 관찰된다. 궤도의 길이가 증가하면 반사파의 영향이 감소하고, 진행파에 의한 파동 특성이 지배적으로 나타나면서 무한 궤도의 특성이 발생한다. 이때 클램핑 시스템의 이산 지지에 의해 pinned-pinned 공진 특성이 나타나는 것을 확인하였다. 구축한 궤도 모델의 길이가 증가할수록 진동 특성은 무한 궤도의 파동 특성과 유사하게 나타나지만, N ≥ 50에서는 수렴하는 특성을 확인했다. 무한 궤도 특성을 모사하기 위하여 길이를 무작정 크게 증가시킬 경우 계산 시간이 오래 걸릴 우려가 발생함으로 이 연구에서는 N = 50으로 설정하여 이론 전달함수를 계산하였고 Newton-raphson 수치해석법을 이용하여 주파수 별 이산 지지된 궤도에서의 레일 등가 물성을 계산한다.

3.4 궤도의 Pinned-pinned 모드 특성

열차 궤도의 pinned-pinned 공진이란 두개의 인접한 체결 장치로 인한 진동 특성으로 레일 마모의 주요한 원인이다. 이때 궤도의 반 굽힘 파장은 체결 장치 사이의 거리와 같으며 식 (8)을 이용하여 모드 주파수를 계산할 수 있다.

f p p = π 2 L 2 E I ρ A

(8)

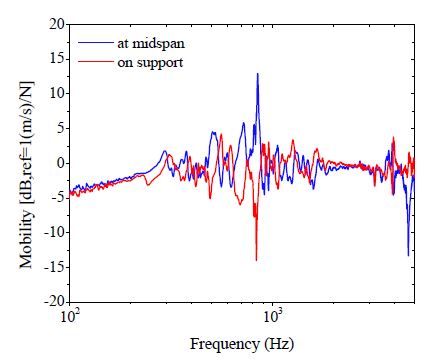
Fig. 9는 실제 궤도의 1차 pinned-pinned 공진주파수를 확인하기 위한 모빌리티(mobility) 전달함수의 측정결과이다. 체결 장치로 인한 모드는 845 Hz에서 발생하는데, 이때의 레일 경간과 지지점에서의 모빌리티는 비교적 큰 차이(8.2 dB)가 발생하였다. 이것은 KRS50 레일 보의 물성을 이용하여 계산한 1차 pinned-pinned 모드 주파수(866 Hz)와 유사하게 나타났다.

Fig. 9

Comparison of the measured mobility at mid-span and on support, respectively

3.5 이산 지지 궤도에서의 레일 물성

Fig. 10은 궤도 파동 전파 특성 해석 모델을 이용하여 예측한 이산 지지 궤도에서의 레일 등가 물성이다. 계산 결과 레일의 등가 굽힘 강성은 4.156 MNm², 손실 계수 0.021로 확인되었다. KRS50 레일의 물성 값은 EI = 4.32 MNm², η = 0.02로서 이 연구에서 제안한 모델을 이용하여 예측한 레일의 등가 물성과 유사하게 나타나는 것을 확인하였다⁽⁹⁾. 따라서 제안한 모델을 이용하여 이산 지지 궤도의 등가 레일 물성을 측정할 수 있고, KRS50 레일 외 타 종류의 레일에서도 적용이 가능할 것으로 예상한다.

Fig. 10

Variation of the dynamic properties of rail on the discrete supports

4. 결 론

이 연구에서는 이산 지지된 궤도에서의 레일 물성을 계측하기 위한 실험 방법을 제안하였다. 정확한 예측을 위하여 하중에 따른 레일 패드의 물성 변화를 고찰하였고 레일 패드의 동적 물성들을 도출하였다. SFC장치와 레일 패드 효과로 인한 체결 시스템의 등가 강성을 모사하기 위하여 클램핑 시스템 모델링을 제안하였고 등가 강성을 계산하였다. 전달함수법을 이용하여 이산 지지된 궤도를 모델링하였고, 궤도 길이에 따른 응답 특성을 해석하였다. 궤도의 길이가 짧으면 이음매에서 발생하는 반사파의 영향이 지배적으로 나타나면서 유한 보의 전달함수 특성들이 관찰된다. 궤도의 길이가 증가하면 반사파의 영향이 감소하고, 진행파에 의한 파동 특성이 지배적으로 나타나면서 무한 궤도의 특성이 관찰된다. 무한 궤도의 특성을 모사하기 위한 레일 모델링을 사용하여 무한 궤도의 전달함수를 예측하였고, 실험 전달함수와 유사한 진동 특성을 확인하였다. 수치해석법을 이용하여 주파수 별 이산 지지된 궤도에서의 레일 등가 물성을 계산하였다. 인천 2호선 열차 궤도의 등가 굽힘 강성은 4.156 MNm², 손실 계수 0.021로 확인되었고 KRS50 레일의 스팩 물성과 유사하게 나타나는 것을 확인할 수 있다. 따라서 제안한 방법으로 다양한 종류의 이산 지지 궤도의 등가물성 측정이 가능할 것이다.

기 호 설 명


A :	단면적
E :	영률
I :	면적 관성 모멘트
ρ :	밀도

Acknowledgments

이 연구는 2020년 대한민국 국토교통부 산하 국토교통과학기술진흥원(20CTAP-C152264-02)의 국토교통기술촉진연구사업 지원을 받아 수행되었습니다.

References

Ahn, S., Kwon, S., Hwang, Y.-T., Koh, H.-I., Kim, H.-S. and Park, J., 2019, Complex Structured Polymer Concrete Sleeper for Rolling Noise Reduction of High-speed Train System, Composite Structures, Vol. 223, e110944. [https://doi.org/10.1016/j.compstruct.2019.110944]
Thompson, D. J., 2008, A Continuous Damped Vibration Absorber to Reduce Broad-band Wave Propagation in Beams, Journal of Sound and Vibration, Vol. 311, No. 3-5, pp. 824~842. [https://doi.org/10.1016/j.jsv.2007.09.038]
Thompson, D. J. and Vincent, N., 1995, Track Dynamic Behaviour at High Frequencies, Part 1: Theoretical Models and Laboratory Measurements, Vehicle System Dynamics, Vol. 24, Sup.1, pp. 86~99. [https://doi.org/10.1080/00423119508969617]
Vincent, N. and Thompson, D. J., 1995, Track Dynamic Behaviour at High Frequencies, Part 2: Experimental Results and Comparisons with Theory, Vehicle System Dynamics, Vol. 24, Sup.1, pp. 100~114. [https://doi.org/10.1080/00423119508969618]
Bae, Y. H. and Kim, M. C., 2013, Conformity Assessment of Vertical Static Stiffness Test Method for Rail Pad, Journal of the Korean Society for Railway, Vol. 18, No. 1, pp. 33~42. [https://doi.org/10.7782/JKSR.2015.18.1.33]
Park, J., 2005, Transfer Function Methods to Measure Dynamic Mechanical Properties of Complex Structures, Journal of Sound and Vibration, Vol. 288, No. 1-2, pp. 57~79. [https://doi.org/10.1016/j.jsv.2004.12.019]
Kim, S. J., Yoo, S.-Y., Jeong, Y., Jun, J.-H. and Park, J.-H., 2006, Measurement of Dynamic Properties of Concrete Structures Using Beam Transfer Function Method, Proceedings of the KSNVE Annual Autumn Conference, pp. 950~953.
Kim, S. J., Lee, J.-P., Park, J.-H and Jeon, J.-H., 2008, Measurement of Viscoelastic Properties of Damping Materials Using Beam Transfer Function Method, Proceedings of the KSNVE Annual Spring Conference, pp. 286~289.
Ryue, J. S. and Jang, S. H., 2013, Comparison of Track Vibration Characteristics for Domestic Railway Tracks in the Aspect of Rolling Noise, Journal of the Korean Society for Railway, Vol. 16, No. 2, pp. 85~92. [https://doi.org/10.7782/JKSR.2013.16.2.085]

Jie Jin received his B.S. of Mechanical Engineering from Liaoning University of Technology in 2012. He worked at the Beijing-Hyundai Motor Technical Center from 2012 to 2015. He is a Ph.D. course student in Acoustics and Vibration Laboratory at Hanyang University. His research interests include structure vibration, railway vibration, passive vibration damping using damper.

Junhong Park received his B.S. and M.S. from the Korea Advanced Institute of Science and Technology (KAIST) in 1991 and 1993, respectively. He worked at the Samsung Electronics Co. Ltd. from 1993 to 1998. He received his Ph.D. from Purdue University in 2002. He is currently a professor of Department of Mechanical Engineering, Hanyang University. His research interests include signal processing, wave analysis, and noise control for improving damping, or machine learning performance including mechanical issue.