탄소강화플라스틱 소재의 복합 가진에 따른 동특성 분석
© The Korean Society for Noise and Vibration Engineering
Abstract
The modal parameter of a carbon-fiber-reinforced plastic(CFRP) can be obtained through frequency response functions. It has been reported to vary with operational conditions, temperature, spectral loading patterns, as well as the direction of the carbon fibers. Previous studies have shown the sensitivity of modal parameters to three parameters. For example, five specimens were used to conduct a uniaxial excitation test by changing the direction of the carbon fibers. The effect of the spectral loading pattern was only evident for the modal damping coefficient of CFRP specimens and two different spectrum patterns, random and harmonic, were applied for uniaxial excitation. In this study, the mixed mode was considered to evaluate the sensitivity of modal parameters of CFRP specimens; the uniaxial excitation condition used was the same as that in previous studies. The mixed mode of excitation is also known as the sine-on-random(SOR) mode and is frequently applied in the military as an advanced vibration test code. The modal parameters from the mixed mode were compared to the results of the conventional single mode, random and harmonic, and the dynamic behavior of CFRP specimens was evaluated under the mixed excitation condition.
Keywords:
Mixed Excitation Mode, Carbon-fiber-reinforce Plastic, Dynamic Analysis, Uniaxial Excitation, Modal Parameters키워드:
복합 가진 모드, 탄소강화플라스틱 소재, 동적 해석, 단축 가진 시험, 모달 파라미터1. 서 론
최근 이동수단에서 연비를 향상시키기 위해 경량 소재에 대한 산업의 요구를 반영하여 마그네슘, 엔지니어링 플라스틱이 대체재로 검토되고 있으며, 탄소강화플라스틱 소재(carbon-fiber-reinforced plastic, CFRP, 이하 탄소복합 소재로 명명)도 차세대 경량 소재로 많이 연구가 이루어져 있다(1~12). 탄소복합 소재는 복합소재의 한 형태로 단일 방향으로 강성이 매우 큰 탄소섬유(carbon fiber)의 특성을 효율적으로 활용하기 위해 탄소섬유를 고분자 수지(polymer resin) 등으로 함침한 후 시트 형태로 만들어 사용된다. 탄소복합소재에 대한 기계적 특성은 해당 제품이 개발되는 과정에서 많은 연구가 이루어졌으며 동적 특성에 대해서도 관련 연구가 진행되었다(13~15).
최근 탄소복합소재를 활용하여 동적 특성을 평가하는 과정에서 영향을 주는 인자들에 대해 연구를 수행하였다. 3가지 탄소섬유 방향에 대해 준비된 시편과 가진 패턴(랜덤, 하모닉)에 대해 시험을 수행하여 탄소복합소재의 동적 특성인 모달 파라미터 변수들(공진점, 모드 감쇠 계수)에 대한 영향도를 민감도 해석 기법을 활용하여 실험적으로 검증하였다(16). 이후 연구에서는 온도 챔버를 활용하여 5가지 탄소섬유의 방향성을 가진 시편에 대해 단축가진 시험을 실시하였으며, 온도와 탄소섬유 방향이 모달 파라미터들에 영향을 주는 것을 확인하였다(17). 가장 최근 연구에서는 탄소복합소재의 동적 특성이 온도 조건, 외부 가진 진동 패턴 및 탄소복합소재의 탄소섬유 방향에 대해 서로 관계를 확인하였다(18). 이러한 조건에서 진동 패턴들은 단지 랜덤 가진과 하모닉 가진 2가지만을 고려하였기 때문에 민감도 해석을 수행하는 과정에서도 케이스 검증이 다소 부족하였다. 따라서 진동 패턴에 대한 다른 추가적인 연구는 진동 패턴의 기여도를 검증하는데 필요하다.
이 연구에서는 기존 진동시험에 통상적으로 사용되는 랜덤이나 하모닉 가진 이외에 2가지 가진모드를 동시 인가하는 복합 모드를 추가하여 탄소복합소재의 동적 특성을 평가하는 것이 연구 목적이다. 최근 랜덤과 하모닉 가진을 동시에 가진하는 복합모드는 sine-on-random(SOR) 가진 모드라고 불리며 가진 시험 시간을 줄이거나 실제 가진 조건을 반영하기 위해 최근 활용도가 높아지고 있다(19). 서로 다른 5개의 탄소섬유 방향성을 가진시편에 대해 단축가진 시험을 수행하였으며, 온도 조건은 – 8 ℃ ~ 105 ℃로 선정하였다. 측정된 주파수응답함수를 활용하여 모달 파라미터를 추출하였으며 해당 분석 방법은 기존 연구들(16~18)과 동일하다.
2. 탄소복합소재 동적 모델
기계 시스템의 동적 특성을 평가하기 위해 입력과 출력의 비율로 나타내어지는 주파수응답함수가 사용된다. 해당 함수는 시스템이 선형성을 충분하기 가진다는 가정 아래 사용되는 일반적인 함수이며, 비선형 특성이 있는 시스템에서도 특정 조건에서 선형성이 보장된다면 해당 함수의 사용이 가능하다(20, 21). 식 (1)은 모드 좌표계에서 단일 입력(F(ω)), 단일 출력(R(ω))에 대한 응답 특성을 보여준다.
| (1) |
여기서,는 i번째 모드에 대해 레지듀얼(residual), 공진점(resonance frequency), 모달감쇠(modal damping coefficient) 값을 각각 나타낸다. 공진점(ωn,i)은 측정된 주파수응답함수들을 활용하여 공통 첨점에서 찾을 수 있으며, 모드 감쇠 값(ξi)은 공진점 및 인근 2개의 반동력점 ()에 의해 식 (2)로 얻을 수 있다.
| (2) |
주파수응답함수를 모달 파라미터인 공진점과 모드 감쇠 변수를 활용하여 3가지 관심 변수들(온도 T, 가진 패턴 p, 탄소섬유 방향 θ)을 고려하면 식 (3)과 같다(16,18).
| (3) |
여기서, 식 (3)을 통해서 탄소복합소재의 주파수응답함수는 3가지 관심 변수에 종속적임을 나타내고 있으며, 특히 이 연구에서 관심을 둔 가진 패턴은 모드 감쇠에만 영향을 주는 것을 알 수 있다. 일반적으로 공진점과 모드 감쇠 계수 값은 시스템의 고유 특성이므로 변화하지 않지만, 탄소 섬유의 방향(θ), 외부 온도(T)에 따라 시스템의 강성 및 감쇠 계수에 영향을 주게 된다. 특히, 감쇠 계수의 경우 추가적으로 가진 패턴(p)에 종속적인 변수가 된다.
3. 모달 파라미터 추출
3.1 단축 가진 시험
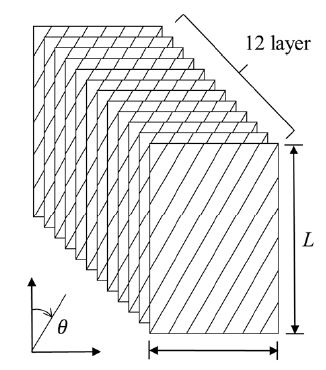
탄소복합소재의 동적 특성을 평가하기 위해 기존 연구와 같이 5가지 방향(0°, 30°, 45°, 60°, 90°)에 대한 시편을 준비하였다(19). SK화학에서 제조한 두께 0.25 mm, 프리프레그 소재(prepreg: USN 250A)를 단일 방향으로 12층으로 쌓은 뒤 고온, 고압으로 성형하는 핫 프레스(hot press) 공법을 사용하여 큰 모재를 제조하였다. 이후 Fig. 1과 같이 5개의 각도별로 절단하여 시편을 준비하였다. 탄소 섬유는 도레이사의 T700(12 K), 함침용으로 사용되는 메트릭스(matrix)는 에폭시 레진으로 구성되었다. 탄소 섬유와 레진의 질량 비율은 64 %와 36 %로 구성되어 있다.
단축 가진기는 시편과 지그의 전체 무게를 반영하여 최대 하중이 50 kg인 단축 가진기(LW127.141-225, Labworks)를 사용하였으며, 가진기의 컨트롤러(VibPilot)는 M+P International사의 제품을 사용하였다. 이 장비를 활용하여 기존 가진 패턴인 랜덤, 하모닉 가진을 수행하였으며, 복합 모드인 랜덤과 하모닉을 동시 가진하는 이벤트도 추가적으로 실시하였다. 가진기의 온도 조건을 제어하기 위해 환경 챔버(EN-VTH-602-V/ENEX, 9.5 KW)를 구비하여 단축 진동을 다양한 온도에서 수행하도록 준비하였다. 아래 Fig. 2는 온도 챔버를 포함하여 환경 진동 시험 장비를 보여준다.
Fig. 1의 직사각형 탄소복합소재 시편에 대해 7개의 가속도 센서를 활용하여 응답을 측정하였으며, 1개의 하중 데이터를 단축 가진기의 지그 부위에 부착하여 하중 데이터를 계측하였다. Fig. 3과 같이 단축진동 시험을 수행하면서 7개의 가속도들과 입력 힘 데이터를 동시에 측정하였다. 측정 위치는 시편의 전체 거동(global mode)이 측정될 수 있도록 균일한 간격으로 센서를 부착하였다. 지그는 최소 주파수 공진점을 4000 Hz 설계하였기 때문에 1000 Hz 이하에서 나타나는 공진은 모두 탄소복합소재의 동적 특성이라고 볼 수 있다. 단일 가진프로파일은 Table 1로 정리하였으며, 복합 모드는 2가지 가진 조건이 동시에 진행하는 것이다. 하모닉 가진은 sine sweep 형태로 진행하여 10 Hz에서부터 60 Hz/min 조건으로 500 Hz까지 증가시켰으며, 랜덤 가진은 white noise 형태로 동일 시간(8분 10초)으로 가진 하였다. 온도 조건은 – 8 ℃, 20 ℃, 50 ℃, 80 ℃, 105 ℃로 5가지 조건으로 시험을 진행하였다.
3.2 주파수응답함수 측정
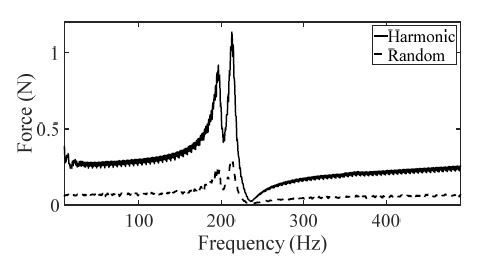
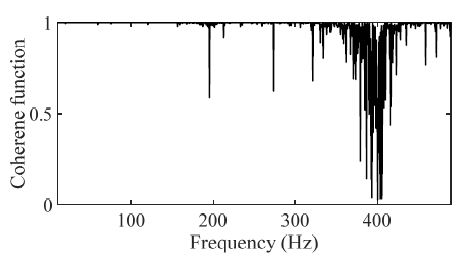
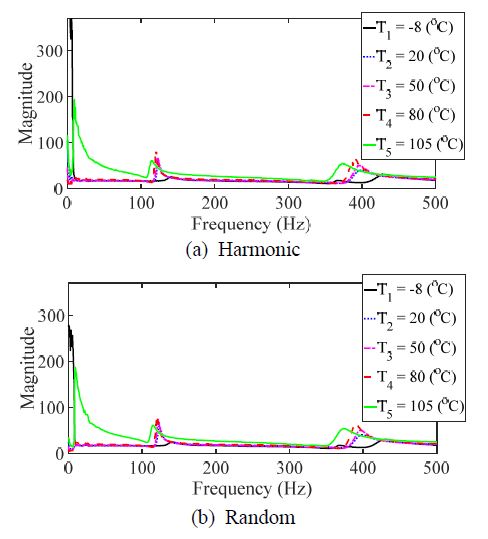
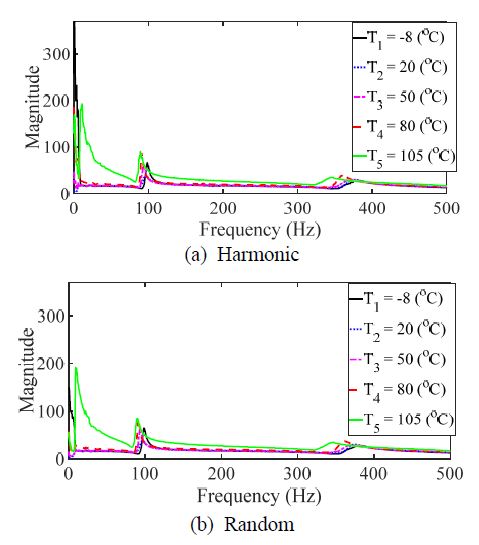
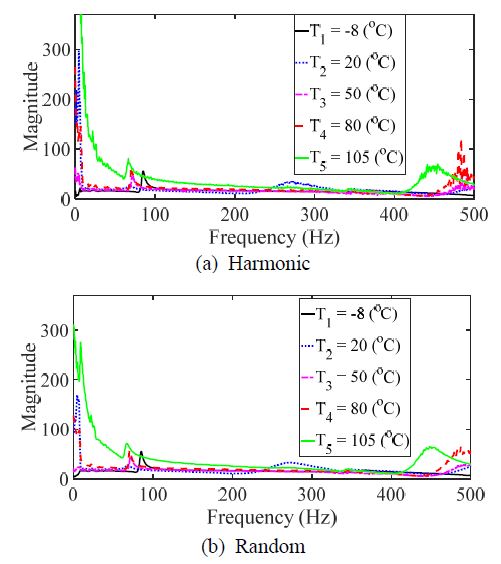
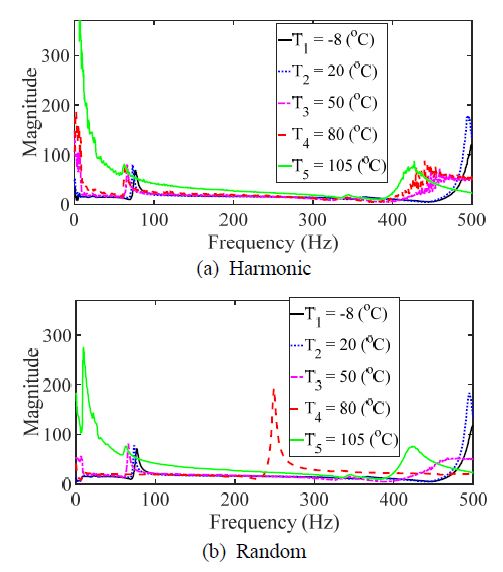
탄소복합소재의 동적 특성을 측정하기 위한 방법으로 단축 가진 시험을 수행하였다. 단축 가진 모드는 Table 1에 의거 개별 시험을 수행하였으며, 이 연구에서는 기존 연구 결과를 그대로 활용하였다(18). 복합 진동모드는 2가지 진동 가진 패턴을 동시에 인가하여 응답 특성을 확인하였다. 탄소 섬유의 방향에 따라 0°, 30°, 45°, 60° 및 90°에 대해 시편을 #1 ~ #5로 각각 명명하였다. 특히, 복합모드 조건에서 단일 가진 조건들(랜덤, 하모닉)과 각각 동일하게 분석을 수행하기 위해 주파수응답함수를 획득하는 과정에서 랜덤 조건은 시간별로 측정된 주파수응답함수들을 평균을 하였으며, 하모닉 조건은 피크 값을 추출하였다. Fig. 4는 시편 #1에 대해 2가지 가진 패턴에 대한 입력 하중 스펙트럼이며, Fig. 5는 해당 시편에 대해 랜덤 가진 조건에서 매 순간마다 측정되는 coherence 값들 중 예시로 2초 ~ 2.1초 순간에 측정한 coherence 함수를 보여준다. Fig. 4를 통해 2개의 입력 패턴이 유사함을 알 수 있으며, Fig. 5를 통해 측정된 주파수응답함수가 충분히 신뢰성이 있음을 알 수 있다. 특히, coherence 함수에서 하모닉 가진은 peak hold 방식으로 주파수응답함수를 측정하였기 때문에 coherence 함수를 전체 주파수에서 얻어내는 것이 어렵기 때문에 도시를 별도 하지 않았다. Fig. 6에서 Fig. 10까지의 그래프는 각 시편에 해당하는 측정 결과이다.
4. 동적 특성 분석
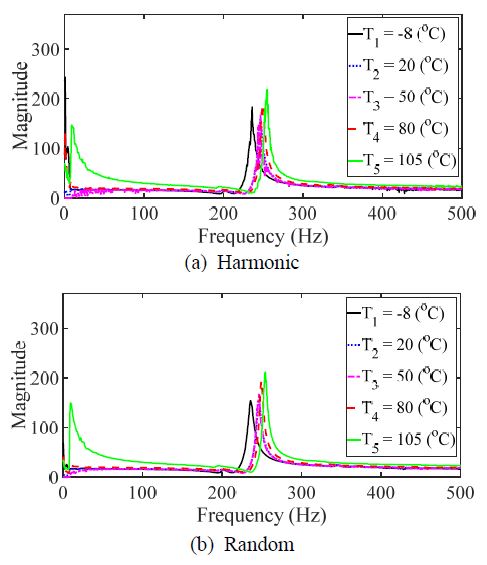
주파수응답함수를 활용하여 단축 가진 시험을 통해 계측된 힘과 가속도 데이터들을 활용하여 공진점과 모드 감쇠 값에 대해 분석을 수행하였다. 단축 가진기를 통한 단일 입력에 대해 7곳에서 동시에 가속도를 측정하였기 때문에 신호처리 관점에서 SIMO (single-input/multi-output) 조건이며, 모달 파리미터를 추출하기 위해 모든 7개의 측정 주파수응답함수들의 각 주파수별 값을 선형 합(linear summation) 조건으로 합하여 하나의 대표 주파수응답함수를 만든 후 모달 파라미터를 추출하는데 활용하였다. Table 2와 Table 3은 기존 연구를 통해 획득된 공진점과 모드 감쇠 값을 보여준다. Table 4와 Table 5는 이 연구에서 복합 진동 모드에 대해 측정된 데이터를 통해 주파수응답함수로부터 계산된 공진점과 모드 감쇠 값을 정리한 것이다.
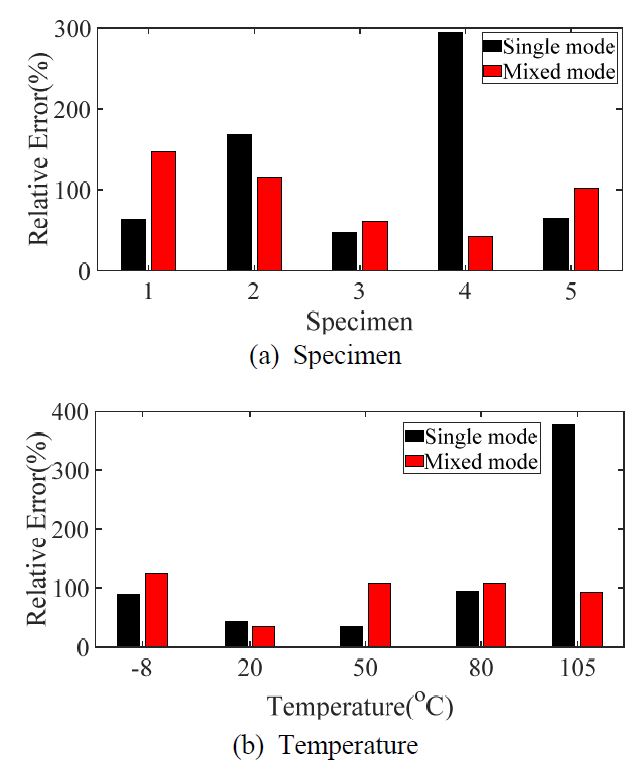
탄소복합소재의 이론적 주파수응답함수와 관련된 식 (3)에서 공진점은 입력 주파수 패턴에 무관하고, 모드 감쇠 계수가 진동 패턴에 대한 함수였다. 동적 특성을 나타내는 Table 2에서 Table 5의 그래프에서 공진점은 이론적 모델에서와 같이 진동 패턴의 영향도가 매우 낮음을 확인할 수 있다. 하지만 모드 감쇠 특성의 경우에는 하모닉 모드와 랜덤 모드에서 약간씩의 차이가 있음을 알 수 있다. 이를 명확하게 확인하기 위해 시편에 대한 상대오차의 합, 온도에 따른 상대오차의 합에 대한 결과를 Fig. 11에 도시하였다.
Fig. 11(a), Fig. 11(b) 그래프에서 오차가 크게 부각되는 이유는 Table 3에서 시편 #4(각도 : 60°)에서 105 ℃ 특정 상황에서 오차가 크게 발생하였기 때문이다. 이를 특정 상황으로 제외를 하고 전체적으로 살펴보면 Fig. 11(a)에서 시편에 따라 오차의 크기 정도가 단일 가진 모드와 복합 모드 조건에서 특별한 경향성을 보이지 않는다. 다만, 시편 #1이 강성이 가장 크기 때문에 상하 진동 조건에서 가장 적합한 시편 조건이기 때문에 시편 #1에서 오차가 상대적으로 크게 나타난 것은 큰 고려 대상이다. Fig. 11(b)에서 온도에 따른 상대오차의 경우를 살펴보면 105 ℃에서 기존 단일 가진 모드가 매우 큰 오차를 보여주고 있으나 해당 조건을 제외하고는 대체적으로 복합 진동 모드에서 상대오차의 값이 더 큰 것을 알 수 있다.
기존 연구에서 단일 모드에 대한 상대오차를 바탕으로 민감도 해석을 진행하였고 해당 과정에서 기존의 연구 결과(Table 2, Table 3)를 그대로 사용하였다(18). 단일 가진 패턴 조건과 비교하여 복합모드는 하모닉과 랜덤 가진이 동시에 수행되기 때문에 외부 가진 패턴에 민감한 모드 감쇠 값은 변화가 작을 것으로 예상할 수도 있었다. 하지만 이 연구에서 실험적으로 복합 모드 조건에서 도출된 모드 감쇠 계수 값을 단일 모드에서 획득한 결과와 비교한 결과 오차가 오히려 더 증가하고 민감도 결과도 변화가 발생하였다.
따라서 기존 연구에서 밝힌 진동 가진 패턴의 차이는 단순히 2개의 패턴을 섞인 것만으로 유사성을 보이지 않으며 별도의 다른 진동 패턴임을 도출할 수 있다. 따라서 탄소복합소재의 감쇠 계수에 영향을 주는 민감도에 복합 모드는 2가지 단일 모드와 별개의 다른 가진 패턴에 해당한다.
복합 모드의 진동 패턴은 참고문헌 (19)에 규정한 바와 같이 특정 상황에서 나타날 수 있고, 계측 위치에 따라서 복합 모드가 나타날 수 있다(22). 따라서 탄소복합소재를 활용하여 이동수단 등에 활용될 경우 모드 감쇠 계수의 값이 단일 모드들과 복합 모드에 유사하게 영향을 주는 것을 알 수 있다. 특히, 복합 모드에서는 단일 모드의 경우와 비교하여 오차의 범위가 커지는 것을 실험적으로 보였기 때문에 더 주의가 필요하다고 판단된다.
5. 결 론
탄소복합소재의 동적 특성은 공진점과 모드 감쇠 계수로 나타낼 수 있으며, 외부 조건인 온도, 진동 가진 패턴과 내부 조건인 탄소 섬유의 방향이 동적 특성 측면에서 영향을 준다는 것을 단축 가진 실험을 통해 재차 확인하였다. 특히 기존 연구에서의 한계였던 가진 패턴 2가지를 확대하여 복합 모드를 고려하여 모드 감쇠 계수의 변화를 살펴보았다. 시험 결과 복합 모드는 단순 모드의 조합이 아니라 별도의 패턴 이벤트라는 것을 알 수 있었으며, 복합 모드에서의 오차는 단일 모드에서의 경우 대비 증가되는 경향도 온도 조건에서 확인하였다. 따라서 탄소복합소재의 동적 특성을 식별하는 과정에서 복합 모드의 진동환경에 노출될 경우 개별 단일 모드들의 결과를 통해 유추할 수 없기 때문에 특별한 주의가 필요하다.
Acknowledgments
이 논문은 부경대학교 자율창의학술연구비(2019년)에 의하여 연구되었습니다.
References
-
Darby, A, Ibell, T. and Evernden, M., 2010, Innovative Use and Characterization of Polymers for Timber-related Construction, Materials, Vol. 3, No. 2, pp. 1104~1124.
[https://doi.org/10.3390/ma3021104]

-
Curtin, W. A., 2000, Tensile strength of Fiber-Reinforced Composite: III. Beyond the traditional Weibull Model for Fiber Strengths, Journal of Composite Materials, Vol. 34, No. 15, pp. 1301~1332.
[https://doi.org/10.1177/002199830003401503]

-
Khan, S. U., Li, C. Y., Siddiqui, N. A. and Kim, J. K., 2011, Vibration Damping Characteristics of Carbon Fiber-reinforced Composites Containing Multi-walled Carbon Nanotubes, Composites Science and Technology, Vol. 71, No. 12, pp. 1486~1494.
[https://doi.org/10.1016/j.compscitech.2011.03.022]

-
Lopez-Puente, J. and Li, S., 2012, Analysis of Strain Rate Sensitivity of Carbon/Epoxy Woven Composites, International Journal of Impact Engineering, Vol. 48, pp. 54~64.
[https://doi.org/10.1016/j.ijimpeng.2011.05.008]

-
Xie, X., Li, X. and Shen, Y., 2014, Static and Dynamic Characteristics of a Long-span Cable-stayed Bridge with CFRP Cables, Materials, Vol. 7, No. 6, pp. 4854~4877.
[https://doi.org/10.3390/ma7064854]

-
Shukri, A. A., Darain, K. M. and Jumaat, M. Z., 2015, The Tension-stiffening Contribution of NSM CFRP to the Behavior of Strengthened RC Beams, Materials, Vol. 8, No. 7, pp. 4131~4146.
[https://doi.org/10.3390/ma8074131]

-
Wickaksono, S. and Chai, G. B., 2015, Life Prediction of Woven CFRP Structure Subject to Static and Fatigue Loading, Composite Structures, Vol. 119, pp. 185~194.
[https://doi.org/10.1016/j.compstruct.2014.08.017]

-
Fasana, A, Ferraris, A., Airale, A. G., Polato, D. B. and Carello, M., 2017, Experimental Characterization of Damped CFRP Materials with an Application to a Lightweight Car Door, Shock and Vibration, Vol. 2017, Article ID. 7129058.
[https://doi.org/10.1155/2017/7129058]

-
Zhang, Y., Yang, Y. E., Du, W. and Han, Q., 2019, Research on Finite Element Model Modification of Carbon Fiber Reinforced Plastic(CFRP) Laminated Structures based on Correlation Analysis and an Approximate Model, Materials, Vol. 12, No. 16, Article No. 2625.
[https://doi.org/10.3390/ma12162623]

-
Waqas, H. M., Shi, D., Imran, M., Khan, S. Z., Tong, L., Ahad, F., Zaidi, A. A., Iqbal, J. and Ahmed, W., 2019, Conceptual Design of Composite Sandwich Structure Submarine Radome, Materials, Vol. 12, No. 12, Article No. 1966.
[https://doi.org/10.3390/ma12121966]

-
Lin, P. C., Fang, J. C., Lin, J. W., Tran, X. V. and Ching, Y. C., 2020, Preheated(Heat-Assisted) Clinching Process for Al/CFRP Cross-tension Specimens, Materials, Vol. 3, No. 18, Article No. 4170.
[https://doi.org/10.3390/ma13184170]

-
Pavlovic, A., Sintoni, D., Fragassa, C. and Minak, G., 2020, Multi-objective Design Optimization of the Reinforced Composite Roof in a Solar Vehicle, Applied Sciences, Vol. l0, No. 8, Article No. 2665.
[https://doi.org/10.3390/app10082665]

-
Zhang, S. H. and Chen, H. L., 2006, A Study on the Damping Characteristics of Laminated Composites with Integral Viscoelastic Layers, Composite Structures, Vol. 74, No. 1, pp. 63~69.
[https://doi.org/10.1016/j.compstruct.2005.03.008]

-
Kim, C. J., 2016, Dynamic Analysis of Carbon-fiber-reinforced Plastic for Different Multi-layered Fabric Structure, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 4, pp. 375~382.
[https://doi.org/10.5050/KSNVE.2016.26.4.375]

-
Kolesnyk, V., Peterka, J., Kuruc, M., Simna, V., Moravcikova, J., Vopat, T. and Lisovenko, D., 2020, Experimental Study of Drilling Temperature, Geometrical Errors and Thermal Expansion of Drill on Hole Accuracy when Drilling CFRP/Ti Alloy Stacks, Materials, Vol. 13, No. 14, Article No. 3232.
[https://doi.org/10.3390/ma13143232]

-
Kim, C. J., 2019, Sensitivity Analysis of the Frequency Response Function of Carbon-fiber-reinforced Plastic Specimens for Different Direction of Carbon Fiber as well as Spectral Loading Pattern, Materials, Vol. 12, No. 18, Article No. 2983.
[https://doi.org/10.3390/ma12182983]

-
Kang, H. Y., Kim, C. J. and Lee, J., 2020, Modal Damping Coefficent Estimation of Carbon-fiber-reinforced Plastic Material Considering Temperature Condition, Materials, Vol. 13, No. 12, Article No. 2872.
[https://doi.org/10.3390/ma13122872]

-
Kim, C. J., 2020, Temperature-dependent Dynamic Characteristics of Carbon-fiber-reinforced Plastic for Differerent Spectral Loading Patterns, Materials, Vol. 13, No. 22, 5238.
[https://doi.org/10.3390/ma13225238]

- MIL-STD-810G Committee, 2008, Environmental Engineering Considerations and Laboratory Tests, Department of Defense Test Method Standard; Department of Defense: Washington, DC, USA.
- Ewins, D. J., 2000, Modal Testing, 2nd Edition, Research Studies Press, Baldock, England.
- Inman, D. J., 2014, Engineering Vibration, 4th Edition, Pearson, Boston, USA.
-
Kim, C. J., 2017, Accelerated Sine-on-random Vibration Test Method of Ground Vehicle Components Over Conventional Single Mode Excitation, Applied Sciences, Vol. 7, No. 8, Article No. 805.
[https://doi.org/10.3390/app7080805]


Chan-Jung Kim received Ph.D. degree from Seoul National University in 2011. He was senior researcher at Korea Automotive Technology Institute over 12 years(2003-2015). Since 2015, he has been joined as the faculty of Pukyong National University, where he is associate professor of Mechanical Design Engineering. His research interests are in the area of the vibration fatigue, noise and vibration issue of mechanical systems.