FE 모델향상 기법을 이용한 세장한 아치구조의 경계조건 결정
© The Korean Society for Noise and Vibration Engineering
Abstract
For a long time, finite element analysis was widely used as an analytical tool to predict the modal parameters of large civil structures such as frequencies and mode shapes. However, their predicted responses normally do not correlate well with those observed because of the physical uncertainties inherent in the boundary conditions, and material properties that are engaged during the mass and stiffness estimations in the FE model. A modal parameter-or an FRF-based finite element model updating procedure can effectively address the aforementioned issue by varying the structural parameters based on the optimization theory, resulting in a highly reliable FE model. This paper demonstrates how a numerical or mathematical model can be iteratively updated to closely match with the global responses of the physical model. In this study, a slender arch structure for green houses is considered as a test specimen. Using an impulse hammer, an input-output modal test is performed, and its natural frequencies and mode shapes are extracted using an advanced system identification, called PolyMAX. Additionally, the test specimen is numerically modeled using ANSYS and a common in-house program, which can be directly exported to a FE model updating tool. The modal parameters or FRFs extracted from a series of vibration records are used as the reference data for updating the initial finite element model by varying the stiffnesses of the members and base or connection springs in a 3-dofs. Finally, it is found that the updated finite element model shows sufficient improvement in the correlation between the test and analysis results in terms of the modal parameters or FRFs, while the latter case scatters more.
Keywords:
Buckling, Eigenvalue Analysis, Input-output Modal Analysis, FE Model Updating, Finite Element Analysis, Film-covered Green House, FRF, 2nd-order Analysis, Snow Load, Slender Arch, System Identification키워드:
좌굴, 고유치해석, 입력-출력 모드해석, 유한요소 모델향상, 유한요소해석, 비닐하우스, 주파수 응답함수, 2계 해석, 설하중, 세장한 아치, 시스템판별1. 서 론
비닐하우스 등과 같은 임시성격의 농촌시설구조물은 강재 파이프로 제작된 아치구조, 단순철물을 사용한 접합방식, 필름커버 사용, 단순 매립기초 등을 대표적인 특징으로 들 수 있다(1). 폭설에 의한 이러한 구조물의 파괴형상은 아치의 휨 혹은 전체좌굴 등에 의하여 발생함을 알 수 있는데, 파괴를 유발하는 핵심인자를 보다 명확히 도출하고, 이에 따른 구조물의 수직 하중지지 능력을 결정하기 위하여서는 현재의 시설구조물이 포함하는 접합 및 기초상태, 아치종류 및 하중상태 하에서 과다 적설하중에 의하여 파괴될 수 있는 다양한 구조물의 파괴양상을 실제와 가깝게 재현할 수 있는 실험방법의 개발이 요구된다. 종래 재하실험에 의하여 비닐하우스와 같은 매우 세장한 구조물의 수직하중에 의한 전체좌굴하중을 결정하기에는 하중재하 및 측정방법 등에 심각한 어려움이 발생한다.
비닐하우스와 같이 곡선 프로파일(profile)이며, 매우 가느다란 구조물의 좌굴하중을 결정하기 위하여서는 전체구조물 레벨에서 구조적 결함(잔류응력, 비수직성과 같은 기하학적 결함, 접합부에 존재하는 편심, 부재의 초기 휨 등)을 고려한 완전 2계-해석(full 2nd-order analysis)이 요구된다. 일반 사각형 골조와는 달리 전체구조물과 부재 레벨의 기하학적 결함의 구분은 하지 않는다. 기존 연구에 의하면 완전 2계-해석에 영향을 미치는 주요 요소로서는 파이프 부재의 모멘트-곡률 관계가 일반 2선식 항복모델과는 달리 상당량이 감소하며, 소성 진행 과정에서보다 심한 비선형 부분을 포함하고 있다는 점이다(2). 이외에도 기초부의 구속상태가 지지력에 큰 영향을 미치는 것으로 알려져 있다. 실제로 비닐하우스 구조물의 기초부는 부분고정 상태이며, 고정의 정도는 토질조건에 따른 매립길이, 앵커의 사용 등에 따라 달라진다. 국내 일반 실무에서 아치의 매립길이는 50 cm 이상을 요구한다. 또한 주 아치에 연결되는 수평 가로대 부재의 구속 작용도 접합조건에 따라 어느 정도 영향을 미칠 것으로 판단된다.
따라서 전체구조물의 결함 정도를 결정하는 문제가 임시 구조물 성격을 나타내는 비닐하우스 아치 구조물의 내력 산정에서 주요 요소가 된다. 기존 연구는 전체구조물의 결함은 1차 고유모드의 형상으로부터 결정하거나, 이에 상응하는 등가 수평하중을 결정하여 가력하는 방법을 추천하고 있다(2). 결과적으로 실험강도와 2계-탄소성 해석, 1계-탄성 혹은 2계-비선형 좌굴해석으로부터 획득한 해석강도를 비교하여 전체적인 결함치를 제안하고 있다.
이외에도 수직하중이 부가되지 않은 구조물에 비하여 수직하중이 부가된 구조물의 고유치는 감소하며, 고유주파수가 0이 될 때의 수직하중을 탄성좌굴을 유발하는 하중으로 간주할 수 있다는 기본 생각에 근거하여 이 진동실험을 계획하게 되었다(3,4).
이러한 목적 이외에도 이 연구에서 개발하고자 하는 진동계측에 의한 구조물의 성능평가기술은 전체구조물의 수직 및 수평방향 강성결정, 동적거동을 결정하는 고유치 추출, 기초부의 고정상태, 연결부의 접합상태 등과 같은 불확정 구조(ξ)변수(uncertain structural parameters)를 결정하여 보다 합리적인 해석모델의 구축하고 더 나아가서는 손상정도를 감지하여 구조물의 건강상태를 상시 평가하는 등의 내용을 포함한다(5).
2. 충격햄머에 의한 모달실험
2.1 시험체 및 실험방법
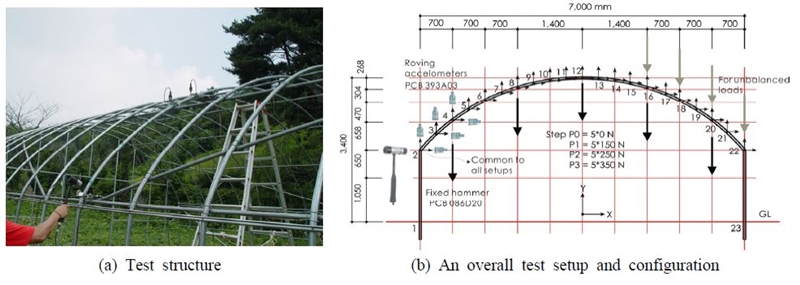
시험체로 제작된 비닐하우스는 2008년 농림수산식품부 고시 내재해기준 시설물(1)에서 제안하는 07-단동-3으로서 길이 10.0 m, 폭 7.0 m, 높이 3.4 m, 적설심 50 cm 및 풍속 36 m/s를 지지하도록 설계된 구조이다. 제작된 시설물 구조의 전체형상 및 관련상세는 Fig. 1과 같다. 아치는 직경(d) 31.8 mm, 두께(t) 1.5 mm, 가로대 및 대각선재는 직경 25.4 mm, 두께 1.5 mm의 강재 파이프(SPVHS)를 각각 사용하였다.
실험대상 아치는 내부에 위치한 아치로서 수평 가로대는 연결되어 있으나, 대각선재 및 면내 수직 및 수평 보조재가 없는 순수 아치에 가까운 형태를 취하고 있다. 센서부착 및 햄머타격을 용이하게 하기 위하여 비닐외피는 씌우지 않았다.
실험에 사용된 센서는 ICP Type의 1축-가속도계로서 PCB 393A03(1 V/g, 0.3 Hz ∼ 1000 Hz, ± 5 g)이며, 충격햄머는 ICP Type의 force sensor가 내장된 PCB 086D20 (0.23 mV/N, ± 22 000 N)이다(6). 데이터획득장치(data aquisition, DAQ)는 16 ch의 벨기에 LMS사(7)의 pimento로서 24 bit, 50 Hz∼50 000 Hz까지 다양한 sampling rate, 0.316 V∼10 V까지 4단계의 input range 등의 사양을 보유하고 있다.
아치구조의 고유진동수 및 모드형태를 결정하기 위한 이 실험은 Fig. 1(b)에서 보는 바와 같이 고정된 한점(절점 2)에서 수평방향으로 충격을 가하고, 수평 및 수직방향 6개의 가속도계를 1 setup으로 하여 10번을 반복 측정한 후, 다음 절점으로 2조의 센서만 이동하는 방법을 택하여 전체 10 setups을 구성하여 한 개의 아치에 대한 실험을 완료하였다(8). 센서의 부착면이 곡면인 관계로 곡면에 센서를 부착할 수 있는 특별장치의 제작이 필요하였으며, 한 절점에서 센서는 X, Y 방향으로 나사로 고정하여 부착물에 연결하였다. 햄머 팁은 저주파에 적합한 soft 재질을 사용하였으며, 대략 햄머력의 크기는 100 N∼200 N을 유지하였고, 이에 따른 가속도의 크기는 20 m/s2 정도였다. Sampling frequency = 200 Hz, input range = 3.16 V(센서) 및 10 V(햄머), pretrigger = 1 %, force window = rectangular 10 %, exponential window = decay constant 0.25, block resolution = 1024 등의 LMS의 TestXpress(7) option을 사용하였다.
2.2 실험결과
내부아치에 대한 충격햄머 실험으로부터 획득한 입력 및 출력기록을 사용하여 고유진동수(f), 모드형태(ϕ) 및 감쇠율 등과 같은 구조성능을 추출하기 위한 일련의 모달해석을 수행하였다.
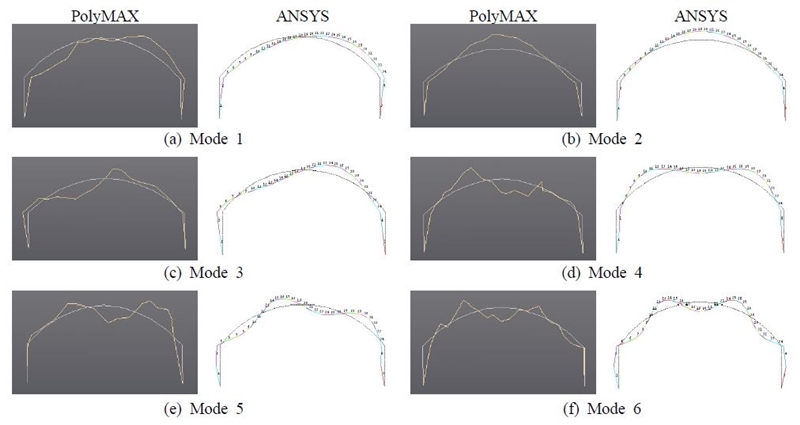
LMS사의 TestLab(7)에서 제공하는 모달해석은 표준방법인 PLSCE(polyreference least-squares complex exponential)(9) 및 PolyMAX(polyreference least-squares complex frequency domain)(10) 등인데, 충격실험 모듈로부터 획득한 block time 데이터에 일련의 수학적 계산을 통하여 가공한 FRF(frequency response function)를 최종적으로 저장하고, 이를 모달해석의 입력데이터로 사용하고 있다. 그 후에는 선택된 데이터에 대하여 pole 및 모드형태 산정, 안정화도(stability diagram) 작성 및 실제 pole 선택, animation 등 일련의 단계를 거쳐 구조성능을 추출하고, 최종적으로 실험과 모달이론에 의하여 합성한 FRF로부터 산정한 모드형태의 관계를 MAC(modal assurance criterion) 등을 통하여 검증하고 있다. 충격하중 및 응답진동기록에 PolyMAX 시스템판별법을 적용하여 추출한 고유진동수 및 감쇠비는 Table 1과 같으며, 또한 저차 모드형태는 Fig. 2와 같다.
PLSCE는 매우 산란된 안정화도를 나타내므로 더 이상 고려하지 않았다. 한편, ANSYS(11)를 사용한 유한요소해석으로부터 획득한 모드형태와 PolyMAX로부터 추출한 모드를 비교하였으며, 현재로서는 5차~6차 모드까지 유효한 것으로 판단되었다(Table 1).
실험 및 해석절차에 관한 보다 자세한 내용은 참고문헌 (12)를 참조하라.
3. FE 모델향상
모델향상이란 FE 해석결과와 실험치와의 차이를 정성적으로 분석하여, 입력변수의 값을 수정하여 실험결과와 일치하는 FE 해석모델을 구축하는 일련의 과정이라 정의할 수 있다.
실제상황을 모사한 FE 해석모델은 종종 물리적 및 수치적 불확실성을 포함한다. 물리적 불확실성으로는 경계조건, 접합부 강성 및 재료의 기계적 성능 등을 들 수 있으며, 수치적 불확실성은 수학적 모델링 및 이산화 오류, 인간의 실수 등에 기인한다. 이외에도 불확실성은 제작상의 허용오차, 작동조건 등에도 영향을 받는다. 이러한 부정확성을 극복하기 위하여 변수를 사용한 모델향상기법은 최근 들어 많은 주목을 받고 있다(5).
이 연구에서는 임시 구조물 성격의 세장한 파이프 아치구조를 대상으로 동적측정으로부터 획득한 고유주파수 및 모드형태 혹은 FRF를 이용하여 기초부 고정정도 및 수평부재의 구속정도를 주요변수로 하여 모델향상을 시도하였다. ANSYS 해석모델은 탄성 혹은 비탄성좌굴을 고려한 2계-해석을 수행하였다.
모델향상은 단계 1: FE 해석모델 구축, 단계 2: 해석모델의 import, 단계 3: 실험으로부터 추출한 모달계수 import, 단계 4: 실험치와 해석치의 비교, 단계 5: 수렴조건 setup, 단계 6: 변수선택, 단계 7: 해당변수에 대한 민감도 해석, 단계 8: 수렴조건이 만족 될 때까지 반복계산 등으로 구성된다(13).
목표 응답치로서 선정된 고유진동수 혹은 모달변위와 같은 개개 모달변수에 대한 오차, 전체 상관정보를 나타내는 MAC 혹은 질량에 대한 오차를 나타내는 여러 상관계수는 아래와 같다. 서로 다른 응답치는 예상되는 상대오차(CRi)를 사용하여 가중치를 달리 부가하였다. 해석치와 실험치의 오차는 N개의 고유진동수에 대하여 weighted relative difference (CCMEAN) 혹은 weighted absolute relative difference (CCABS), 모드형태에 대하여 average MAC (MACMEAN 혹은 CCMAC) 등으로 식 (1) ~ (3)과 같이 표시한다.
| (1) |
| (2) |
| (3) |
여기서 MAC(ϕa,ϕe) = |{ϕa}H{ϕe}|2/{ϕa}H{ϕa}) ({ϕe}H{ϕe}) 이며, k1은 가중치이다.
고유진동수 및 모드형태와 마찬가지로 FRF 값(α)에 대하여 사용한 전체 및 국부 상관관계는 식 (4) ~ (7)과 같다.
| (4) |
| (5) |
| (6) |
| (7) |
여기서 SAC(signature assurance criterion), AFAD(average FRF amplitude difference)는 FRF의 전체유사성 지표이며, CSAC(cross signature assurance criterion), CSSF(cross signature scale factor)는 국부적 유사성 지표로서, 각각 FRF의 형상 및 크기의 유사성을 나타낸다. CSAC는 고유진동수 정점값의 위치 및 양을 평가하기 때문에, 질량 및 강성변화에 매우 민감하다.
4. 모델향상 결과
전술한 모델향상을 위하여, 이 연구는 상용패키지인 MATLAB(14) 및 FEMtools(15)에서 제공하는 여러 모듈을 이용하여 일련의 해석과정을 구축하였다. Bayesian 변수산정 기법을 사용하여 고유진동수 및 모드형태 혹은 FRF의 일치를 시도하였다.
재료의 탄성계수(E) 및 밀도(ρ), 아치의 단면적(Α) 및 휨강성(Ι), 수평 가로대 및 지지점의 구속조건 (kx, ky, kθ)을 변수로 하여 여러 경우의 모델향상을 시도한 결과, 여기에서는 실험결과와 충분히 일치하고, 가장 물리적인 설명이 가능한 결과를 제공하는 2가지 경우에 대하여서만 기술한다.
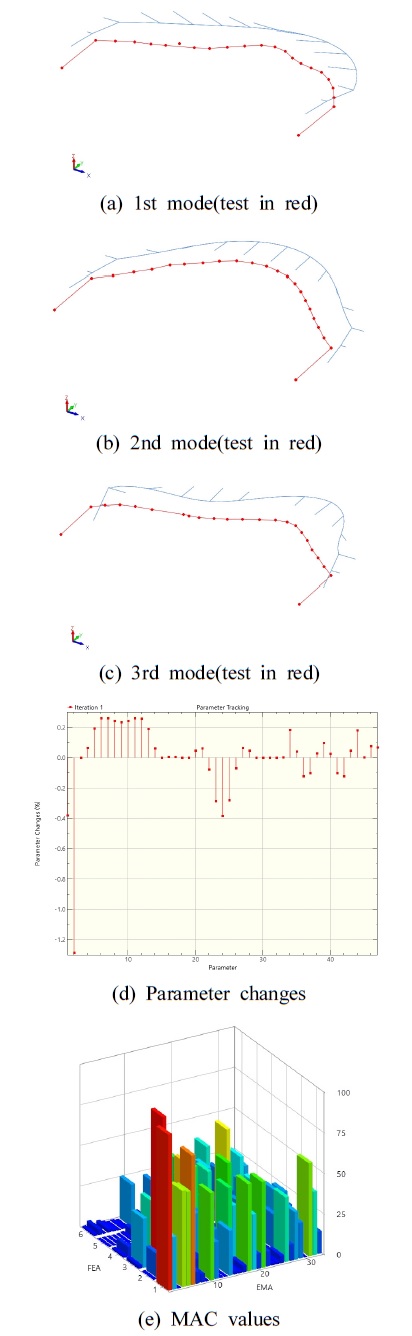
Table 2 및 Fig. 3은 초기 ANSYS 해석모델에서 수평 가로대 및 지지점에서의 구속조건을 묘사하기 위하여 해당 위치에 3-자유도의 스프링을 사용하였다.
기본적으로 재료의 강성 및 밀도를 추가적인 전체 변수(global parameter)로 고려하여 전체 50개의 변수를 사용하여 모달계수에 대한 일치를 시도한 결과이다. 6차 모드까지 고려하였으나, 3차 모드까지만 유효한 결과를 나타내었다. 대체로 변수의 최대변화값은 강성 및 질량에서 ±1.5 % 정도이며, 스프링 강성의 변화는 ±0.5 % 미만이었다. 이는 초기 ANSYS 해석결과가 상당히 정확한 값을 예측하고 있기 때문인 것으로 판단된다.
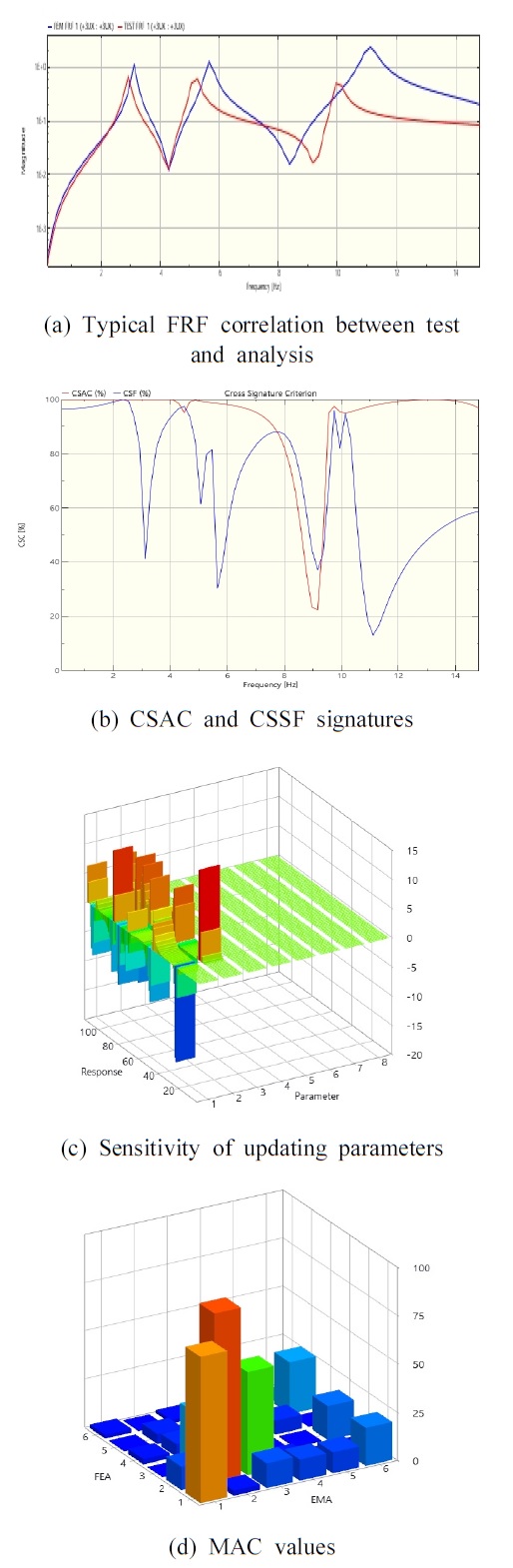
Fig. 4는 재료의 강성 및 밀도, 지지점만의 3-자유도 스프링 강성을 변수로 하여 FRF에 대하여 일치를 시도한 결과이다. 재료의 강성 및 밀도를 추가적인 전체 변수(global parameter)로 고려하여 전체 10개의 변수를 사용하여 모달계수에 대한 일치를 시도한 결과이다. FRF 산정은 가진 주파수에 대하여 운동방정식의 해를 산정하는 형식의 직접법을 사용하였다. FRF는 해당 위치에서의 출력응답/입력하중으로 표시할 수 있는데, 이는 단위크기를 갖는 하중을 가력하여 운동방정식의 해를 구하는 것과 동일하다. 이 경우에는 수평 가로대의 구조조건을 묘사하는 스프링은 포함하지 않았다. 고유진동수 및 모드형태를 이용한 향상과는 달리 FRF를 사용하는 경우 FRF 및 모달계수에서 상당한 오차를 나타내고 있음을 알 수 있다. Fig. 4(b)의 CSAC 및 CSSF는 실험 및 해석 FRF의 대표적 차이를 정량적으로 보여주고 있다. FRF의 경우 2차 모드 까지만 유효한 것으로 보인다. 이는 실험으로부터 발췌한 FRF의 정확도에도 크게 의존하는데, 이 연구의 세장한 아치의 구조의 경우 연결된 인접부재의 영향으로 정확도가 높은 실험결과를 확보하기가 매우 어렵기 때문인 것으로 판단된다. 대체로 변수의 최대변화값은 강성 및 질량에서 ± 10 % 정도이며, 스프링 강성의 변화는 미미하였다.
5. 결 론
임시성격의 세장한 비닐하우스 아치구조에서 현행 실무에서 사용하는 지지부 시공 및 수평가로대 연결에 의한 구속정도를 알아보기 위하여 일련의 입력-출력 모달실험 및 FE 모델향상을 수행한 결과, 아래와 같은 결론을 유도할 수 있었다.
(1) 동적계측실험으로 획득한 모달계수에 근거하여 지점에 3-자유도의 스프링을 포함한 FE 해석모델의 향상을 시도해본 결과 현행 50 cm 이상의 매립길이를 갖는 비닐하우스 기초부의 지지조건은 고정단에 가까운 것으로 나타났다. 하지만 하중조건 및 진동모드가 증가함에 따라 고정도는 저하될 것으로 예상된다.
(2) 수평 가로대의 구속정도를 묘사하는 연결부의 3-dof 스프링 강성은 전체 업데이트된 해석결과에 무시할 정도인 것으로 나타났다. 이는 조리개 등의 임시방법으로 접합을 하기 때문인 것으로 판단된다.
(3) 대체로 변수의 최대변화는 모달계수에 근거하여 향상을 시도하였을 경우 강성 및 질량에서 ± 1.5 % 정도이며, 스프링 강성의 변화는 ± 0.5 % 미만이었다. 또한 FRF에 의하여 향상을 시도하였을 경우 강성 및 질량에서 ± 10 % 정도이며, 스프링 강성의 변화는 미미하였다.
(4) FRF를 이용한 FE 모델향상 결과는 고유진동수 및 모드형태를 사용한 경우보다 수렴하는데 어려움이 발생하며, 보다 열악한 결과를 나타내었다. 2차 모드 까지만 유효한 것으로 나타났는데, 이는 실험으로부터 발췌한 FRF의 정확도 및 신뢰성과도 밀접한 관계가 있는 것으로 판단된다.
(5) 이 연구에서 개발한 모달계수 혹은 FRF에 근거한 FE 모델향상기법은 실험결과에 물리적인 양을 조정하여 FE모델을 구축하므로 구조물의 거동을 보다 신뢰성 있게 예측, 조사할 수 있다. 따라서 초기에 사용한 여러 구조가정의 오류 여부를 판단할 수 있으며, 더 나아가서는 동일기법에 의하여 구조물의 피해여부, 위치 및 정도 등을 예측할 수 있다.
References
- Ministry for Food, Argriculture, Forestry and Fisheries, 2008, Standard Design Drawings and Specification for Disaster–Resistant Horiticultural Facilities, 2008-76.
- Roux, P., Robertson, A. P. and Motro, R., 1997, The Design of Slender, Monotubular Steel Arches, Structural Engineer, Vol. 75, No. 9, pp. 143~151.
- Lurie, A., 1959, Lateral Vibrations as Related to Structural Stability, PhD Thesis, California Institute of Technology, California, USA.
-
Plaut, R. H. and Virgin, L. N., 1990, Use of Frequency Data to Predict Buckling, Journal of Engineering Mechanics, Vol. 116, No. 10, pp. 2230~2335.
[https://doi.org/10.1061/(ASCE)0733-9399(1990)116:10(2330)]

-
Friswell, M. I. and Mottershead, 1995, Finite Element Model Updating in Structural Dynamics, Kluwer Academic Publishers, Dordrecht, The Netherlans.
[https://doi.org/10.1007/978-94-015-8508-8]

- PCB Piezotronics, 2011, Test & Measurement Sensors & Instrumentaion, MTS System Corp., USA.
- LMS, 2008, TestXpress Version 3A and TestLab Version 9A, Experimental Notes and Manuals, Belgium.
- Ewins, D. J., 2000, Modal Testing: Theory, Practice and Application, Research Studies Press, Hertfordshire, UK.
-
Hermans, H. and Van der Auweraer, H., 1999, Modal Testing and Analysis of Structures under Operational Conditions: Industrial Applications, Mechanical Systems and Signal Processing, Vol. 13, No. 2, pp. 193~216.
[https://doi.org/10.1006/mssp.1998.1211]

-
Peeters, B., Van der Auweraer, H., Guillaume, P. and Leuridan, J., 2004, The PolyMAX Frequency- Domain Method: a New Standard for Modal Parameter Estimation, Shock and Vibration, Vol. 11, No. 3-4, pp. 395~409.
[https://doi.org/10.1155/2004/523692]

- Ansys, 2007, Robust Simulation and Analysis Software, http://www.ansys.com, /, Release 11.0, ANSYS Incorporated, USA.
-
Cho, S. H., 2010, Estimation of Modal Parameters for Plastic Film-covered Greenhouse Arches, Journal of the Earthquake Engineering Society of Korea, Vol. 14. No. 2, pp. 67~74.
[https://doi.org/10.5000/EESK.2010.14.2.067]

-
Cho, S. H., 2019, FE Model Updating of Tall Buildings Using Output-only Modal Data, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 131~140.
[https://doi.org/10.5050/KSNVE.2019.29.1.131]

- The Mathworks, 2005, Using MATLAB, Version 7.0.4, Natick, MA, USA.
- Dynamic Design Solutions, 2020, FEMtools Users’ Guide Version 4.1, Leuven, Belgium.

Soon-Ho Cho is a professor of Architectural Engineering at Gwangju Univ., Gwangju, Korea. He obtained his engineering degrees from Hanyang Univ. for B.S. and M.S. in Architectural Engineering and from McGill Univ. for Ph.D. in Civil Engineering and Applied Mechanics. His research interests include analytical and experimental evaluations of steel-concrete composite members in shear critical regions, and currently dynamic measurements, FE model updating and dynamic inelastic analysis for tall buildings.