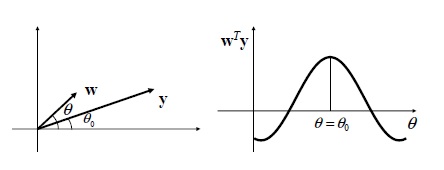수중방사소음 예측을 위한 빔형성 방법 기반 추진기 캐비테이션 음원준위 추정
‡ Recommended by Editor Han Shin Seol
© The Korean Society for Noise and Vibration Engineering
Abstract
In general, the prediction of underwater radiated noise requires source level information. This study proposes a method for the source level estimation of propeller cavitation based on the beamforming method. The proposed method obtains the source level information by determining the source strength corresponding to the estimated cavitation position. As the solution of the minimization problem can be determined analytically rather than numerically, it has the advantage of fast computational time. The proposed method is verified through a model-scale test conducted in a large cavitation tunnel of Korea Research Institute of Ships and Ocean Engineering. The estimated source level of the propeller cavitation matches well with a transfer-function-based method in the frequency band that satisfies the far-field. In addition, another method for reducing the computational time is considered through determining the source level from the cavitation position and sound pressure level.
Keywords:
Underwater Radiated Noise, Source Level Estimation, Beamforming Method, On-board Measurement키워드:
수중방사소음, 음원준위추정, 빔형성 방법, 온보드 계측1. 서 론
선박의 대형화 및 고속화 추세에 따라 프로펠러 또는 수중익에 과도한 부하가 가해지고, 이에 따른 캐비테이션 발생은 추진 효율의 저하 및 진동 등 다양한 문제의 원인으로 지목되고 있다. 캐비테이션의 폐해로는 수중방사소음을 우선 고려할 수 있으며, 캐비테이션 소음에는 프로펠러의 익수/회전수 등과 같은 선박 식별에 필요한 정보를 포함하고 있어 과거에는 소음 성능이 중요한 함정 또는 연구선과 같은 특수선만 관심을 받았다. 그러나 최근 국제해사기구의 수중환경에 대한 보호규제(1)로 선박수중소음이 일정 수준 이하가 되게끔 제한하고 있기에 일반 상선으로도 초점이 확대되는 추세다. 수중방사소음이란 선박 내외에서 발생하는 소음 및 진동이 수중으로 방사되는 소음을 말하며, 그중 프로펠러 회전에 의해 발생하는 캐비테이션은 상선에서 전파되는 소음의 주된 원인, 즉 소음원으로 지목되고 있다.
실선 환경에서 프로펠러 캐비테이션에 의한 수중방사소음을 예측 및 모니터링하기 위해서는 주변 환경에 독립적인 음원준위(source level, SL)의 정보가 필수적이다. 일반적으로는 i) 모형 프로펠러의 소음계측, ii) 전달함수 역산을 이용한 모형 단계에서의 음원준위 추정, iii) 실선 단계로의 확장, iv) 수중방사소음을 예측의 과정을 거친다. 즉, 별도의 전달함수 계측 및 현재까지 미지의 영역인 실선 확장이라는 불확실성 요소를 포함하게 되는데, 만약 운전조건이 달라지면 상기의 과정을 각 조건별로 반복해야 하는 불편함이 따른다. 뿐만 아니라 최근 함정 분야에서 대두되는 이슈와 같이, 아함(我艦) 수중방사소음 모니터링과 관련하여서도 상기의 모형선 계측 기반 방법은 적합하지 않음을 강조할 수 있다.
이 연구에서는 실선의 프로펠러 상부영역에 하이드로폰 배열, 즉 온보드 센서를 설치·사용할 수 있다는 전제하에, 앞서 언급한 문제를 극복하고자 하였다. 다시 말해, 운전조건이 달라지더라도 모형 단계를 거치지 않고 i) 실선에서의 소음계측, ii) 실선에서의 음원준위 추정, iii) 수중방사소음을 예측하고자 하였으며, 이를 위해 빔형성 이론에 기반한 문제 정식화를 통해 음원강도 추정법(2)을 제안하고자 하였다. 물론 실선에 온보드 센서를 설치하는 것은 어려운 일이며, 설치가 가능하더라도 프로펠러 상부영역에서의 캐비테이션 소음 계측은 근거리장(near-field) 계측에 해당할 가능성이 크기에 일반적인 소음저감 모델을 적용하기 어렵다. 또한, 설치할 센서의 개수, 센서배열의 설계 등 많은 사람의 고려가 필요하나, 이 연구에서는 기초 단계로써 제안 방법이 적용 가능한 저주파수 한계 파악을 위해 빔형성 방법 기반의 방법론을 검증하고자 한다.
제안 추정법은 예상 음원강도를 도입한 예측치와 관측치 사이의 오차를 최소화함으로써 기존 빔형성 방법과 달리 음원의 강도를 추정할 수 있다. 또한, 압축센싱(compressive sensing)(3,4) 등과 같은 일반적인 최소화 문제처럼 해를 수치적 혹은 반복적인 방법을 통해 구하지 않고 해석적(analytical)으로 얻을 수 있어 계산시간이 빠르므로 수중방사소음의 실시간 예측 또는 모니터링에 적합함을 강조할 수 있다.
이 연구에서는 프로펠러 캐비테이션의 음원준위 추정을 위한 관련 이론에 대해 설명하고, 캐비테이션 소음 실측 결과에의 적용에 대해 기술한다. 제안 추정법을 이용하여 얻은 음원준위를 검증하고자 모형선 실험을 통해 전달함수를 이용한 기존 방법으로 얻은 결과와 비교하였고, 원거리장(far-field) 계측조건을 만족하는 주파수 영역에서 5 dB 이내의 차이로 두 결과가 상당히 일치함을 관찰할 수 있었다.
2. 프로펠러 캐비테이션 음원준위 추정을 위한 관련 이론
온보드 계측 시스템을 이용하여 프로펠러 캐비테이션 소음을 계측할 시, 일반적으로 소음원은 센서 배열과 비교적 가까운 위치에 존재하기에 근거리 측정 영역에 놓인다. 근거리장 영역에서는 소음원과 배열 센서간 거리의 미세한 변화만으로도 음압준위(sound pressure level, SPL)가 크게 달라지는 요동(fluctuation) 현상이 발생하며, 이때 수반되는 소음방사 현상은 매우 복잡하다. 그러나 여기서는 해석의 단순화를 위해 캐비테이션 소음의 광대역 특성으로부터 유동장에 의한 수력학적 압력 성분은 고려하지 않았고, 선체 구조물에 의한 반사파의 영향을 무시하였다. 또한 캐비테이션 소음원을 단극음원(monopole source)으로 대체하여 구형파로 모형화함으로써, 그 위치는 캐비테이션이 최대가 되는 영역과 일치한다고 가정하였다. 다시 말해 Fig. 1에 나타낸 바와 같이, 어떤 관심공간에 존재하는 소음원에서 방사되는 구형파를 M개의 배열 센서(하이드로폰)로 계측할 경우, m번째 센서에서 계측된 압력값 ym은 그린 함수(green function)(5)를 통해 주파수 영역에서 식 (1)과 같이 나타낼 수 있다.
| (1) |
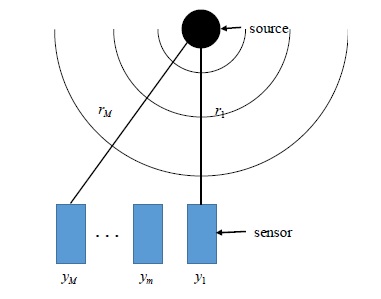
The noise source described by the monopole source with strength is x. mth sensor in the array receives the signal ym
여기서 x[Pa·m]는 단극음원의 강도이고, rm[m]은 단극음원과 m번째 센서 사이의 거리이며, k=(2πf/c)[1/m]는 주파수 f [Hz]에 해당하는 파수(단, c(=1500 m/s)는 음속을 의미함.), 그리고 e는 잡음을 나타낸다. 식 (1)을 M개 센서에 대하여 확장하여 벡터로 나타내면 관측벡터(measurement vector) y∈ℂM는 식 (2)와 같이 표현할 수 있다.
| (2) |
여기서 a∈ℂM는 전파벡터(propagation vector)이고, e=[e1, ..., em]T∈ℂM는 서로 상관관계가 없는 요소로 구성된 가우시안(gaussian) 잡음벡터이며, 위 첨자 T는 전치(transpose)를 나타낸다.
전통적인 빔형성 방법은 Fig. 2에 개략적으로 나타낸 바와 같이, 관심공간 내 가상음원에 대한 주파수와 거리의 함수인 스캔벡터 w=[w1, ..., wm]T∈ℂM를 회전시키며 관측벡터 y와의 내적(빔형성 파워)을 계산하여 두 벡터가 닮음이 되는 방향(θ=θ0), 다시 말해 빔형성 파워 |wTy|가 최댓값을 가지는 각도 θ를 소음원이 존재하는 방향으로 추정한다. 그러나 기존의 빔형성 방법으로는 프로펠러 캐비테이션 소음 음원준위 추정에 필요한 음원강도의 정보를 제공하지 않기 때문에, 식 (3)과 같이 예상 음원강도 E [Pa·m]를 도입한 최소화 문제를 통해 음원강도를 구하고자 하였다(6).
| (3) |
여기서 ||A||F=(∑∑aij2)1/2는 행렬의 크기를 나타내는 프로베니우스 노름(Frobenius norm)이고, Y(=yyH) [Pa2]∈ℂM×M는 관측벡터의 상관행렬(correlation matrix), A(=aaH) [1/m2]∈ℂM×M는 전파벡터의 상관행렬을 나타내며, 위 첨자 H는 켤레 전치(conjugate transpose)를 의미한다.
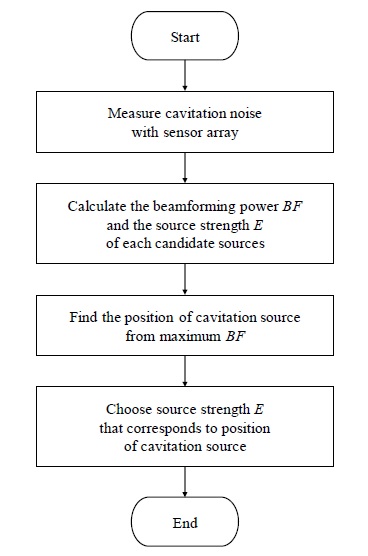
식 (3)을 음원강도(=E)에 대해 풀면 관심공간 내 모든 가상음원에 대한 음원강도를 얻을 수 있으며, 이를 바탕으로 음원의 위치도 추정하게 된다. 이때 여러 가상음원 중 하나가 실 음원에 해당하기 때문에, 음원준위를 구하기 위해서는 먼저 음원의 위치를 구한 후, 그 지점에 대응하는 음원강도 E를 선택함으로써 음원준위를 추정한다. Fig. 3에는 식 (3)을 이용한 음원강도 추정 과정을 순서도로 도시하였다. 여기서 E는 최소자승법(least squares method)(7)을 통해 식 (4)와 같이 구할 수 있다.
| (4) |
여기서 tr(A)=∑aii은 행렬의 대각합(trace)을 구하는 연산자이다.
식 (4)는 식 (3)의 목적함수(=||Y-E2A||F2)를 식 (5)와 같이 전개하여 양변을 E에 대해 편미분한 뒤, 식 (6)과 같이 우변을 0(영)으로 두고 A(=AH)와 Y(=YH)가 허미시안 행렬(Hermitian matrix)임을 이용하여 E에 대해서 정리하면 얻을 수 있다.
| (5) |
| (6) |
또한, 식 (4)를 식 (5)에 대입한 뒤 정리하면 식 (7)과 같이 나타낼 수 있으며, 이를 통해 음원의 위치를 추정할 수 있다.
| (7) |
식 (7) 우변의 첫 번째 항은 관측에만 의존하는 값이므로, 식 (3)을 최소화하기 위해서는 거리에 대한 함수인 두 번째 항이 최댓값을 가져야 함을 알 수 있다. 식 (7)의 물리적 의미를 살피기 위해 관심공간 내 가상음원이 실 음원과 같은 위치에 있는 경우와 그렇지 않은 경우를 비교해 보자.
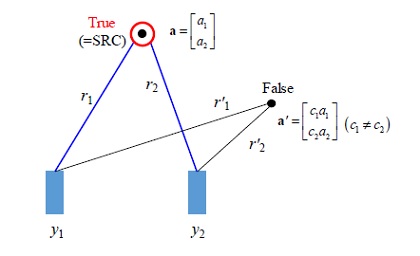
단극음원으로 모형화된 하나의 소음원에서 방사되는 음장을 2개의 배열 센서(=M)로 계측하는 예시를 Fig. 4에 나타내었다. 여기서 적색 원은 실 음원을, 흑색 점은 관심공간 내 임의의 가상음원을 나타내며, r [m]과 r' [m]는 각각 가상음원과 배열 센서간 거리를 나타낸다. 먼저, 가상음원과 실 음원의 위치가 동일한 경우, 가상음원에 대한 전파벡터 a=[a1 a2]T는 관측벡터 y=[y1 y2]T(=xa)와 서로 닮음이기에 식 (7) 우변의 두 번째 항 분모와 분자가 서로 상쇄되어 0이 되며, 식 (3)은 최소값을 가진다. 반면, 가상음원과 실 음원의 위치가 동일하지 않으면 관측벡터 a'=[c1a1 c2a2]T(단, c1≠c2)로 표현되어 y와 닮음이 아니므로 상쇄되지 않아 0보다 큰 값을 가지게 된다. 이를 통해 식 (7)을 이용하면 소음원의 위치가 추정 가능함을 설명할 수 있다.
따라서 관심공간 내 가상음원에 대한 식 (7) 우변의 두 번째 항, 다시 말해 빔형성 파워가 최대가 되는 지점을 소음원의 위치로 볼 수 있으며, 식 (3)은 식 (8)과 같이 수정할 수 있다.
| (8) |
식 (3) 또는 식 (8)은 일반적인 최소화 문제와 같이 해를 수치적 혹은 반복적인 방법으로 구하지 않고 해석적으로 얻을 수 있기에 계산속도가 빠른 장점이 있다. 단, 식 (8)을 비롯하여 앞에서 나타낸 최소화 문제는 주파수 영역에서 정의되었음을 강조하며, 이에 따라 주파수 대역 선정에 대한 문제가 남는다. 그러나 이 연구는 수중방사소음 예측을 위한 음원준위 추정법을 제안하기에 별도의 주파수 대역 선정 없이 계측 가능한 모든 주파수, 즉 샘플링 주파수의 절반을 분석에 사용하였다. 제안 추정법을 이용한 음원준위 추정 과정을 다시 정리하면, 관심 주파수 대역에 대해 식 (4)와 식 (8)을 이용하여 관심공간 내 가상음원에 대한 음원의 강도와 빔형성 파워를 각각 계산한다. 다음, 빔형성 파워가 최댓값을 가지는 지점, 즉 음원의 위치를 찾고 해당 지점에 대응하는 음원강도 E를 선택하여 레벨[dB]로 나타내면 최종해, 즉 음원준위를 얻게 된다.
3. 모형선 실험에의 적용
3.1 실험환경 및 실측자료 분석
제안 음원준위 추정법을 캐비테이션 소음 실측 결과에 적용하고자, 선박해양플랜트연구소의 캐비테이션 터널에서 날개 수가 4개인 프로펠러가 장착된 모형선을 이용한 캐비테이션 발생 실험을 수행하였다.
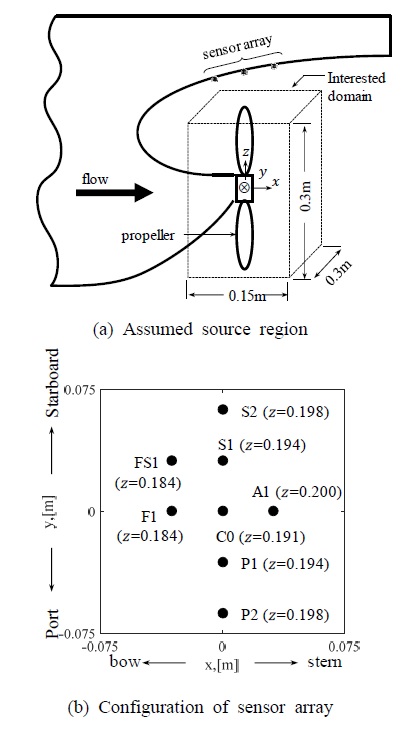
캐비테이션 소음신호 계측에는 B&K 8103 하이드로폰을 사용하였으며, 설치 공간의 제약으로 총 8개의 배열 센서(Fig. 5(b))를 Fig. 5(a)와 같이 프로펠러 상부 선체 표면에 매립하였다. 프로펠러 중심을 원점으로 한 주변 0.15×0.3×0.3 m3의 영역을 가로, 세로, 높이 10 mm 간격의 15 376개 격자로 분할하여 관측 공간(Fig. 5(b))으로 선정하였고, 이를 바탕으로 전파벡터 a를 형성하였다.
터널 내 유속은 7 m/s, 프로펠러의 회전수는 44 rad/s로 고정하였고, 안전 조건을 만족하면서 지속 운전이 가능한 엔진의 최대 출력을 의미하는 최대연속출력(maximum continuos rating, MCR)의 비율 변화를 통해 터널 내 압력을 단계별로 감압시켜 발생된 캐비테이션 소음을 샘플링 주파수 262.14 kHz 기준 60초 동안 계측하였다. 실험 조건은 Table 1과 같고, Fig. 6에는 고속카메라로 관찰된 프로펠러 날개에서의 캐비테이션 형상을 나타내었다.
MCR의 비율에 따라 3개의 실험조건(75 %MCR, 84 %MCR, 100 %MCR)을 선정하였으며, 각각의 터널 내 압력과 캐비테이션 수(cavitation number, σn)는 Table 1과 같다. 이때 식 (9)로 정의되는 캐비테이션 수는 캐비테이션이 발생한 정도를 나타내는 척도로, 값이 작을수록 캐비테이션이 많이 발생했음을 의미한다. 따라서 100 %MCR이 가장 가혹한 실험조건에 해당함을 알 수 있다.
| (9) |
여기서 n [Hz]은 프로펠러의 초당 회전수, D [m]는 프로펠러의 직경, P [Pa]는 터널 내 압력, Pn [Pa]은 포화수증기압(saurated vapor pressure)을 나타낸다.
Fig. 6은 고속카메라를 이용한 실험 조건별 캐비테이션 관찰 결과로, 실험 조건과 상관없이 공통적으로 날개끝에서 길게 늘어진 형태의 보텍스 캐비테이션(Fig. 6(a))과 날개 끝단을 덮는 형태의 시트 캐비테이션(sheet cavitation)(Fig 6(b))이 관측되어 캐비테이션이 충분히 발달된 상황임을 관찰할 수 있었다.
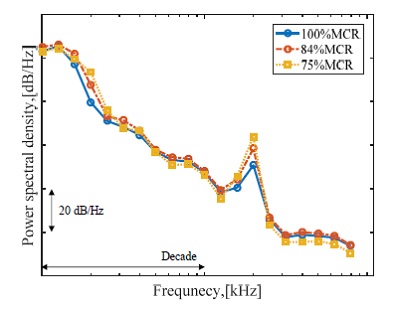
Fig. 7에는 계측된 소음신호 중 음압준위의 수준이 전 주파수 대역에서 가장 높은 A1 채널의 실험조건별 파워 스펙트럼 밀도를 도시하였으며, x축은 로그 단위로 나타내었고 y축의 간격은 20 dB/Hz이다. 주파수 분해능 64 Hz 및 해닝 창문함수(Hanning window function)를 적용하였고, 75 %의 오버랩(overlappaing)으로 641회의 앙상블 평균(ensemble average)을 취해 계산하였다.
일반적인 캐비테이션 소음의 파워 스펙트럼 밀도와 같이 Fig. 7의 그래프는 전체적으로 우하향하는 특성을 보였다(8). 그러나 MCR의 비율이 상승하여도 Fig. 7과 같이 캐비테이션 관측 양상에는 큰 차이가 없던 점에서 알 수 있듯, Fig. 7의 파워 스펙트럼 밀도 역시 눈에 띄는 차이는 드러나지 않았다. 단, 18 kHz~20 kHz 대역에서 피크(peak)가 발생하였음을 관찰할 수 있는데, 이는 프로펠러의 날개 끝단부의 고유진동수와 날개 뒷전(trailing edge of the blade)에서 발생한 와류 흘림(vortex shedding) 주파수가 공진하여 발생하는 프로펠러 명음(propeller singing)(9) 현상과 관련한 것으로 추측된다.
3.2 캐비테이션 음원준위 추정결과
2장에서 언급한 바와 같이, 수중방사소음 예측을 위해 별도의 주파수 대역 선정 없이 캐비테이션 소음의 광대역 특성을 고려한 1 kHz~100 kHz에 대한 자료를 이용하여 제안 추정법을 적용하였다. 관심 대역을 64 Hz로 분할하여 관측벡터 y를 추출하였고, 앞서 결정한 전파벡터 a와 함께 식 (4) 및 식 (8)의 계산을 각 주파수에 대하여 반복하였다.
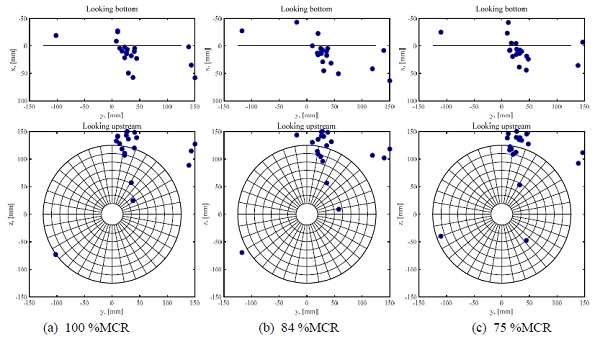
Fig. 8에는 캐비테이션 소음의 위치 추정 결과를 1/3 옥타브 대역에 대해 각 시험조건별로 나타내었고, 각각 위에서 아래로 바라본 방향과 선미에서 선수로 바라본 방향의 그림을 도시하였다. 추정 위치는 시험조건과 상관없이 대부분 일정한 영역에서 군집을 이루었으며, 그 범위는 고속카메라 관찰결과(Fig. 6)와 큰 상관관계를 가졌다. 몇몇 군집을 벗어난 경우는 3 kHz 미만의 저주파수 영역 또는 프로펠러 명음이 발생한 18 kHz ~ 20 kHz 대역 등에 대한 결과이며, 제안 추정법은 음원의 위치를 먼저 구해야 하기에 해당 위치에서의 추정 음원강도는 전달함수를 이용한 기존 방법의 결과와 차이가 발생할 수 있음을 추측할 수 있다.
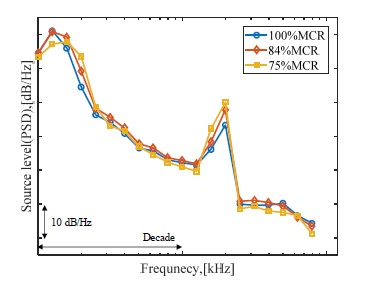
Fig. 9에는 관심 대역에 대한 캐비테이션 소음의 음원준위 추정 결과를 도시하였다. 파워 스펙트럼 밀도(Fig. 7)에서 알 수 있듯이 추정 결과는 전체적으로 우하향하였고 시험조건과 상관없이 유사한 양상을 띠었다. 또한, 18 kHz ~ 20 kHz 대역에서 피크가 발생하였는데, 이는 앞서 언급한 바와 같이 프로펠러 명음 현상과 관련한 것으로 추측된다.
Fig. 10에는 제안 추정법과 기존의 전달함수법을 이용하여 각각 구한 음원준위의 추정결과를 나타내었으며, 시험조건과 상관없이 위치 및 음원준위 추정결과가 유사했기에 가장 가혹한 100 %MCR 조건의 결과만 도시하였다. 제안 추정법은 각 주파수에 대한 음원의 위치 및 온보드 센서까지의 거리를 구할 수 있기에, 이 거리가 파장을 2배한 값보다 커지는 주파수인 3 kHz(Fig. 10의 검은색 선)를 원거리장 영역이 시작되는 경계로 선정하였다. 3 kHz 미만의 주파수 대역에서는 눈에 띄는 차이가 나타남을 알 수 있는데, 이는 전통적인 빔형성 방법의 저주파수 한계로 인해 잘못된 위치를 추정한 것으로 판단된다. 반면, 원거리장 영역을 만족하는 주파수 대역에서는 5 dB 이내의 차이에서 비교적 잘 일치함을 관찰할 수 있으며, 이를 통해 빔형성 방법 기반의 방법론을 이용한 제안 추정법으로 실선에서의 캐비테이션 음원준위 추정이 가능함을 확인하였다.
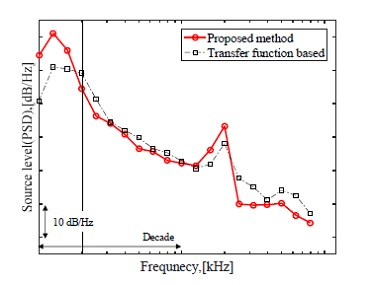
Comparison of source level between the transfer function based- and proposed- method (condition: 100 %MCR)
그러나 제안 추정법을 이용한 분석은 관심 대역(=1 kHz ~ 100 kHz)에서 약 8.2초가 소요되었다. 따라서 수중방사소음의 실시간 추정, 즉 모니터링에는 적합하지 않다고 볼 수 있으나, 이는 관심 대역을 고해상도의 일정 대역폭으로 분할하였기 때문으로 추측된다. 따라서 주파수 해상도를 낮추거나 1/3 옥타브밴드 등을 추정에 적용하면 소요 시간을 단축시킬 수 있다고 판단되었다.
만약, 수면의 반사를 무시할 수 있는 환경, 즉 자유음장(free-field) 환경이라면 식 (1)의 레벨 계산을 표현한 식 (10)을 식 (11)과 같이 정리함으로써 음원준위를 추정할 수 있다.
| (10) |
| (11) |
여기서 Pref=1 μPa이며, 식 (1)의 지수(exponential)항은 크기가 ‘1’이므로 생략하였다
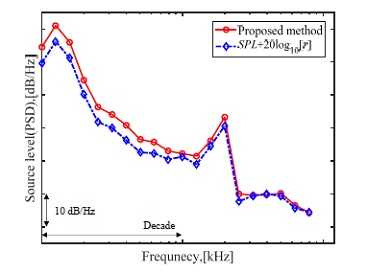
식 (11)을 통해 구한 음원준위와 제안 추정법을 이용하여 얻은 음원준위를 Fig. 11에 도시하였다. 관심 대역에서 두 그래프는 비교적 잘 일치함을 알 수 있으며, 이를 통해 소음원의 위치를 알고 있다면 계측 음압준위에 단순히 거리 정보를 보정함으로써 음원준위 추정이 가능함을 알 수 있다.
4. 결 론
이 연구에서는 수중방사소음의 실시간 추정을 위해 빔형성 방법에 기반한 프로펠러 캐비테이션의 음원준위 추정법을 제안하였고, 모형선 실험을 통해 적용 가능성을 타진하였다. 제안 추정법을 통해 얻은 음원준위의 검증을 위해 전달함수법을 이용하여 구한 결과와 비교하였으며, 원거리장을 만족하는 주파수 영역에서 두 결과가 잘 일치함을 관찰할 수 있었다. 제안 추정법을 이용한 음원준위 추정시, 소음원의 위치 정보를 이용한 음압준위로부터의 추정 등을 검토함으로써 계산시간의 단축 가능성을 확인하였다.
이 연구는 제안 추정법을 실선에 적용하기 전 모형선 실험을 통해 빔형성 방법 기반의 방법론을 검증한 점에서 의미를 찾을 수 있다. 단, 캐비테이션 실측 자료에 제안 기법 적용시 온보드 센서의 개수 및 배열을 임의로 적용하였다. 따라서 개수 선정 및 배열 설계의 문제가 남으며, 최적화 기법을 통해 이를 해결함으로써 제안 추정법의 적용 가능성을 더욱 높일 수 있을 것으로 판단한다. 향후, 자유수면 등의 영향(Lloyd’s mirror effect) 등을 고려한 소음전파모델 개발을 통해 연구의 완성도를 높이고자 한다.
Acknowledgments
이 연구는 한국해양과학기술원 부설 선박해양플랜트연구소의 주요사업 ‘고효율/저소음 선박을 위한 추진기소음 원천기술 개발 및 실선적용 연구(PES3890)’과제의 지원을 받아 수행되었으며 상기 과제 연구 결과의 일부입니다.
References
- International Maritime Organization (IMO), 2011, Report of Marine Environment Protection Committee (MEPC), 62nd Session Agenda Item 19 (62/19), Noise from Commercial Shipping and Its Adverse Impacts on Marine Life - Development of an International Standard for, 2011.
-
Donoho, D. L., 2006, Compressed Sensing, IEEE Transactions on Information Theory, Vol. 52, No. 4, pp. 1289~1306.
[https://doi.org/10.1109/TIT.2006.871582]

-
Kim, Y.-H., Seol, H., Lee, J.-H. and Jeong, H., 2020, Localization and Source-strength Estimation of Tip Vortex Cavitation Noise Using Compressive Sensing, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 4, pp. 329~339.
[https://doi.org/10.5050/KSNVE.2020.30.4.329]

- Foeth, E. J. and Bosschers, J., 2016, Localization and Source-strength Estimation of Propeller Cavitation Noise Using Hull-Mounted Pressure Transducers, In Proceedings of the 31st Symposium on Naval Hydrodynamics, Monterey, CA, USA, pp. 11~16.
-
Pierce, A. D., 2019, Acoustics: An Introduction to Its Physical Principles and Applications, 3rd Ed., Springer, New York.
[https://doi.org/10.1007/978-3-030-11214-1]

- Christensen, J. J. and Hald, J., 2004, Beamforming, Technical Review 1, Bruel & Kjær, Denmark.
- Strang, G., 2006, Linear Algebra and its Applications, 4th Ed., Thomson Brooks/Cole, Belmont, CA.
-
Lee, J.-H., Lee, K.-J. and Park, H.-G., 2018, Exploiting Air-bubble Reflection for Reducing Propeller Caviation Induced Hull Excitation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 6, pp. 730~739.
[https://doi.org/10.5050/KSNVE.2017.27.6.730]

- Kim, T. and Lee, H., 2018, A Study on the identification of Underwater Propeller Singing Phenomenon, The Journal of the Acoustical Society of Korea, Vol. 37, No. 2, pp. 92~98.

Yong-Hyun Kim received his B.S. and M.S. degrees in Mechanical Engineering in 2018 and 2020, respectively, is currently studying for Ph.D. degree at Changwon National University. He especially is interested in Source localization and Source strength estimation.

Hanshin Seol received his B.S. in Aerospace Engineering from Pusan National University in 1998. He received his M.S. and Ph.D. degree in Mechanical and Aerospace Engineering from Seoul National University in 2001 and 2005. He is now a principal researcher and the head of the 'Naval Ship Engineering Research Center' at Korea Research Institute of Ships and Ocean Engineering in Daejeon, Korea. Dr. Seol's current research interests include hydroacoustics, propeller noise and development of propeller noise reduction technology.

Jeung-Hoon Lee received B.S. degree in Mechanical Engineering from Hanyang Univ. in 2001, MS and Ph.D. degrees from KAIST in 2002 and 2007, respectively. After industrial experiences in SSMB of Samsung Heavy Industries Co. Ltd. for 9 years, he in 2016 joined the school of mechanical engineering of Changwon National Univ. as associate professor. His major interests cover signal processing, acoustic cavitation and Etc.

Hongseok Jeong received his B.S. and M.S. in Mechanical and Aerospace Engineering from Seoul National University in 2012 and 2014. He received his Ph.D. degree in Engineering and Physical Sciences at the University of Southampton in 2019. He is currently working at Korea Research Institute of Ships and Ocean Engineering. His research interest is identification and mitigation of propeller noise.