Fourier Expansion Number를 적용한 Beam 요소 기반 유한요소해석모델을 이용한 배관계 탄소성 해석 기법

1. 서 론

최근 동일본 대지진으로 인한 후쿠시마 원자력 발전소 사고 이후 전 세계적으로 가동 원자력 발전소의 새로운 안전성 평가 방법에 대한 논의가 활발하다. 우리나라에서도 2016년 경주 및 2017년 포항에서 각각 진도 규모 5.8, 5.4의 지진이 발생하여 가동 원전의 설계초과지진에 대한 안전성 평가의 필요성이 강조되었다. 미국과 일본뿐 아니라 한국에서도 ASME B&PV Code Section-III와 같은 탄성해석 기반의 설계기준에서는 고려할 수 없는 변형률 기반의 평가 기준을 수립하기 위한 연구를 수행하고 있다. 선행 연구에 따르면, 지진에 의한 배관의 주된 파손 원인이 피로 누적 및 재료 경화에 의한 ratcheting이라는 것을 확인하였다^(1,2). 지진하중에 대해 배관계의 곡관이 주된 취약부위라고 여겨지며, 곡관부의 기하 형상에 따라 취약부위의 위치가 다르게 나타난다. 피로 누적 및 ratcheting 효과를 반영한 평가 기준 수립을 위해서 지진하중에 대한 변형률을 계산할 수 있는 유한요소해석 방법에 대한 연구가 이루어졌다^(3,4). 원자력 발전소 기기는 ASME B&PV Code Section-III에 따라 응력 및 모멘트를 계산하기 위해 pipe 요소를 이용한다^(5,6). Pipe 요소는 Timoshenko beam 이론이 기반이므로 전단응력에 따른 단면의 변형은 무시되기 때문에 탄소성 해석에는 부적합하다. 따라서 shell 및 solid 요소와 같이 단면의 변형을 고려할 수 있는 요소를 이용하여야 한다. 일본 JSME 에서 발간한 원자력 발전소 설계 및 건설을 위한 코드⁽⁴⁾에서는 배관의 탄소성 거동을 확인하기 위해서 단면의 변형을 고려할 수 있는 요소를 사용해서 유한요소해석을 진행하도록 권장하고 있고, 배관의 탄소성 거동을 확인하기 위한 연구에서는 shell 및 solid 요소를 이용한 유한요소해석모델을 통해 실험을 모사하였다^(1,4,12). 현재 기존 발전소 설계 시 사용했던 요소인 pipe 요소 중, 단면의 변형을 고려할 수 있는 요소로 대표적인 것이 elbow 요소이다^(7,8). Elbow 요소는 곡관에 적용하기 위해 개발된 요소로, 배관 단면의 변형에 의해 발생하는 ovalization 및 wrapping 현상을 표현할 수 있다. 곡관의 기하 형상에 따라 Fourier expansion number를 이용하여 단면의 자유도를 부여하여 적절한 수준의 변형을 계산한다. Elbow 요소는 solid 및 shell 요소와는 달리 line body 기반의 요소로 한 절점을 기준으로 부여된 단면 정보에 대해 반복계산을 통해 단면에서의 물리량을 예측하는 방법으로, 요소에 부여된 절점에서 직접계산 및 외삽을 통해 값을 계산하는 solid와 shell 요소와는 차이점이 있다. 이 연구에서는 변형률 기반의 평가를 위해 Fourier expansion number를 적용한 elbow 요소를 적용하여 탄소성 해석을 진행하는 기법에 대하여 연구하였다. 곡관 파손 실험을 solid 요소로 모사한 기준 solid 모델을 기반으로 elbow 요소의 변수 민감도 분석을 통해 최적의 변수 조건을 제시하고, 탄소성 동해석을 위해 배관의 두께비(R/t) 및 곡관의 곡률에 따라 기준 모델과의 응답 비교를 통해 일반성을 확인하였다. 최종적으로 원자력 발전소 1차 냉각재계통의 surgeline 배관에 적용하여 시간이력 탄소성 해석을 진행하여 기준 solid 모델 해석 결과와의 차이를 비교하며 방법론을 검증하였다.

2. 본 론

2.1 Elbow 요소를 이용한 단면변형효과 모사

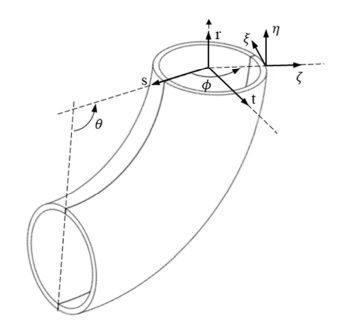
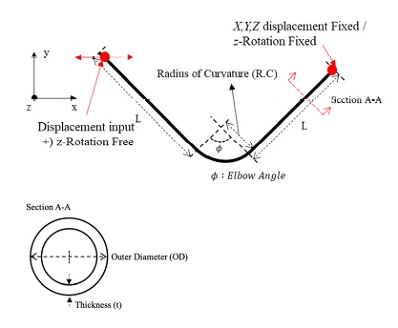
Elbow 요소는 단면의 변형을 나타내기 위해 유한요소해석 과정에서 각 노드 별 원주 방향으로의 변위 계산을 위해 Fourier expansion number를 이용한다^(8,9). 단면이 고정되어 있다는 가정하에 4개의 node를 가지는 elbow 요소에서 각 노드에서의 유한요소해석 변위 계산식은 Fig. 1의 좌표계를 기준으로 식 (1)를 이용한다⁽⁷⁾.

Fig. 1

Elbow element coordinate system

$\[ u_i\left(r,s,t\right)=\sum _{k=1}^4{h}_k{u_i}^k+t\sum _{k=1}^4{\overline{a_k}h}_k{V_{ti}}^k+s\sum _{k=1}^4{\overline{a_k}h}_k{V_{si}}^k \]$

(1)

$\[ {\omega }_{\xi }\left(r,\varphi \right)=\sum _{m=1}^{N_c}\sum _{k=1}^4{h}_k{c_m}^k\sin 2m\varphi +\sum _{m=1}^{N_d}\sum _{k=1}^4{h}_k{d_m}^k\cos 2m\varphi \]$

(2)

$\[ {\omega }_{\zeta }=-\frac{d{\omega }_{\xi }}{d\varphi } \]$

(3)

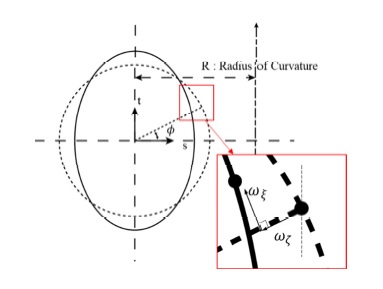
여기서 i는 global 좌표계의 방향을 나타내고, h_k는 k노드에서의 보간함수로, 4개의 노드를 가지는 elbow 요소에 대해서 계산되어 있다⁽⁸⁾. V_t, V_s는 각 방향으로의 단위 벡터이고, a_k는 k노드에서 주어진 요소의 반지름 값이다. 각 노드에서 단면의 변형을 계산하기 위해서 식 (2), (3)을 이용하여 및 Fig. 2와 같은 반복계산이 이루어지는데, Fourier expansion number는 식 (2)에서 원주방향을 따라 단면 변형의 자유도를 결정한다. Fourier expansion number는 기하 형상에 따라 적절한 수준으로 결정되어야 한다. 예를 들어, 두께가 두꺼운 배관에 대해서는, 낮은 m값을 통해 단면의 변형 수준을 제한하여 단면의 변형이 잘 일어나지 않는 현상, 즉 높은 단면 강성을 나타내도록 할 수 있고, 반대로 얇은 배관에 대해서는 높은 자유도를 부가해 반대효과를 반영할 수 있다. 이는 실험을 통해 유효한 값을 찾는 것이 가장 이상적이며, 상용 유한요소해석 프로그램인 ANSYS에서는 key-option을 통해 구현할 수 있다⁽⁹⁾.

Fig. 2

Elbow element sectional coordinated system

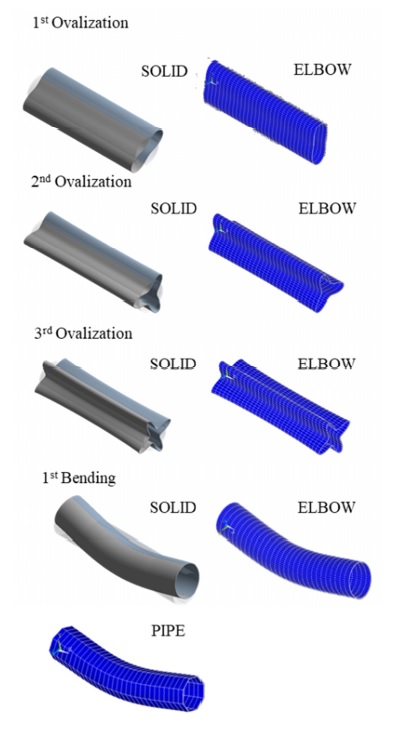
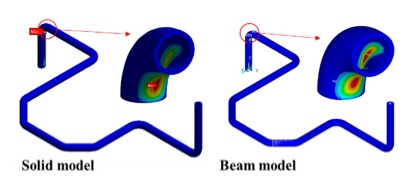
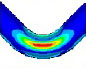
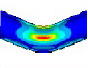
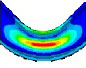
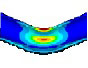
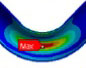
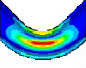
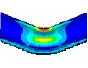
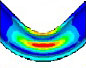
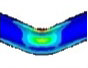
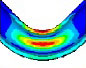
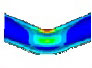
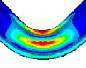
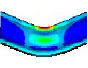
Fourier expansion number의 단면 변형의 효과를 확인하기 위해 solid, elbow, pipe 요소의 모달 해석 결과를 비교했다. 해석 결과 Table 1과 같이, Fourier expansion number를 적용한 경우에 단면의 변형에 따른 모드를 확인할 수 있었다. 모드 형상은 Fig. 3과 같이 solid 요소를 이용한 경우와 Fourier expansion number를 적용한 elbow 요소를 이용한 경우 동일한 단면 변형 모드를 확인할 수 있었지만, pipe 요소를 사용한 경우에는 굽힘 모드만 도출되었다. 이를 통해 Fourier expansion number와 elbow 요소를 이용하여 solid 요소를 이용한 것과 동일한 단면의 변형 효과를 확인할 수 있었다.

Table 1

Straight pipe modal analysis result

Fig. 3

Straight pipe mode shape result

2.2 Elbow 요소 최적 변수 결정

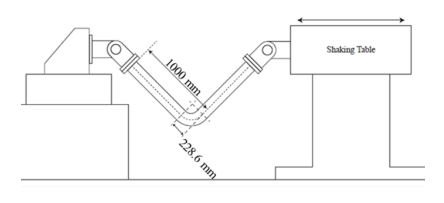
Elbow 요소를 사용한 유한요소해석모델 구축 방법 연구를 위해 JSME benchmark 프로그램의 실험 결과를 기반으로 지배 변수 민감도 분석 수행 및 최적변수를 결정하였다⁽⁴⁾. Benchmark 프로그램은 Fig. 4의 실험구성을 가지고 외경 114.3 mm, 두게 3.4 mm의 배관 단면을 가진다⁽⁴⁾. 해당 실험을 모사한 기준 solid 모델을 구축하고, Fourier expansion number를 적용한 elbow 요소의 지배변수를 선정, 민감도 분석을 수행하여 solid 모델과 가장 동일한 값을 나타낼 수 있는 변수 설정을 도출하였다.

Fig. 4

JSME experiment configuration

실험을 모사한 solid 모델 구축 조건은 benchmark 활동 결과 가장 실험과 차이가 적은 기관의 조건을 사용하였다. 사용된 재료 및 탄성, 탄소성 물성값은 Table 2와 같다. 소성 변형을 나타내기 위한 거동방정식으로는 bi-linear kinematic hardening을 활용하여 항복응력과 2차 접선 계수를 Table 2와 같이 결정했다. 실험 조건을 고려한 경계조건은 양 끝단 힌지부분의 회전 자유도와 가진 방향의 변위 자유도를 부여했다. 또한 shaker table의 질량을 구현하여 입력 가속도로 인한 하중이 전달되도록 하였다.

Table 2

Information of benchmark program

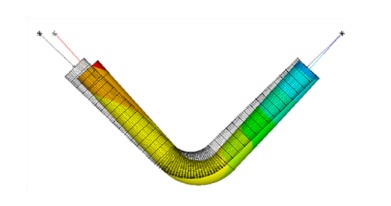
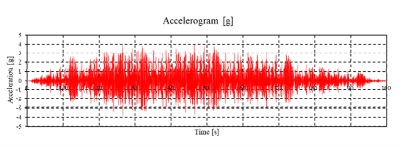
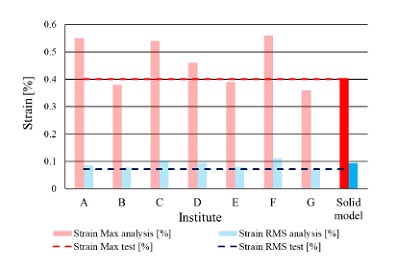
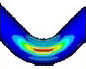
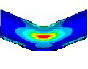
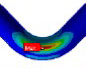
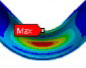
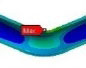
동특성의 동일성 확인을 위해 수행한 모달 해석 결과 고유진동수는 Table 3과 같이 실험 및 solid, beam 모델에서 동일하게 도출되었고, 모드 형상은 Fig. 5와 같이 in-plane 굽힘 형태가 지배적이었다. 이를 통해 실험, solid, beam 모델의 경계조건 및 동특성의 동일성을 검증하였다. 가진 해석에 이용한 입력조건은 Fig. 6의 가속도 입력으로, 층 응답 스펙트럼을 기반으로 ASCE/SEI 43-05에서 정의된 인공지진시간이력 제작 과정을 기반으로 생성된 인공지진파를 이용하였다⁽¹⁰⁾. 해석 결과 Fig. 7과 같이 곡관 crown 내면 위치에서 JSME 실험 결과와 동일한 취약부위가 존재하는 것을 확인했다. Fig. 8에서는 JSME에서 제시한 기준인 최대 hoop strain, hoop strain RMS 값을 비교하여 실험과 동일한 수준의 값을 확인하였다. 따라서 실험 및 참여기관 해석 결과와 비교했을 때 기준값이 JSME에서 제시한 오차범위 내에 존재하고 취약부위도 동일하게 나타나는 것을 통해 구축된 기준 solid 모델이 곡관의 탄소성 거동을 적절하게 나타낼 수 있다는 것을 확인하였다.

Table 3

Modal analysis result of benchmark model

Fig. 5

JSME experiment 1st mode shape

Fig. 6

JSME solid model input accelerogram

Fig. 7

Critical location for experiment

Fig. 8

Institute analysis result and experiment result

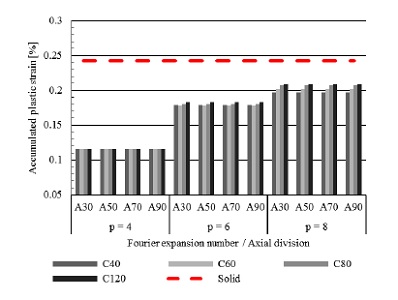
구축한 solid 모델을 이용하여 탄소성 해석에서 elbow 요소의 변수 민감도 분석을 시행하였다. 주요 변수로 원주 방향, 축 방향의 격자 수와 Fourier expansion number를 결정하여 기준 solid 모델과 누적 소성변형률 및 취약부위를 비교하여 최적의 모델링 조건을 도출하였다. 입력 조건은 10 mm의 단순 압축 변위 입력의 정해석을 수행하였고, Table 4의 변수 항목의 조합 조건에 따른 결과를 비교하였다. Fig. 9의 민감도 분석 결과 원주 방향, 축 방향의 적분점 수보다 Fourier expansion number의 영향이 지배적인 것을 확인했다. 해당 민감도 분석 결과를 바탕으로 최적 격자 설정 및 Fourier expansion number는 Table 5와 같이 결정했다.

Table 4

Sensitivity analysis cases

Fig. 9

Sensitivity analysis result

Table 5

Determined optimal parameters

2.3 단순 곡관에 대한 탄소성 해석

2.2절에서 확인한 elbow 요소의 최적 변수 설정을 이용하여 배관계 탄소성 해석을 진행하기 위해 단순 곡관 요소에 대한 case study를 진행하였다. JSME에서 진행한 실험에서는 외경 114.3 mm, 두께 3.4 mm의 얇은 배관을 사용한 것과 달리, 원자력 발전소 1차 냉각재계통과 같이 지진 하중, 내부 유체, 내압에 의한 구조 건전성이 확보되어야 하는 경우 보다 두꺼운 배관이 사용된다. 배관의 종류는 ASME B36.10M에 명시되어 있는 pipe에 대한 size, schedule number로 세분화되어 있는데, size에 따라 외경의 크기가 결정되고, schedule number에 따라 두께가 결정된다. 이 연구에서는 원자력 발전소 1차 냉각재계통에서 취약할 것으로 예상되는 surgeline 배관의 크기인 size 300을 기준으로 시간이력지진해석을 위한 case를 선정하고, elbow 요소를 이용한 탄소성 해석의 유효성을 확인하였다⁽¹¹⁾. Case 선정 시 해석의 보편성 확보를 위해 Sch 40~160에 맞는 두께와 surgeline에 포함된 곡관의 곡률 및 곡률반경, 직관의 길이를 적용하였다. 해석 모델의 형상은 Fig. 10과 같이 V자 형태의 배관으로 선정하였다. 직관의 길이(L)는 3000 mm, 곡률반경(radius of curvature)은 외경의 1.5배인 485.7 mm, 곡관의 곡률은 surgeline의 형상에 포함된 곡률인 90°, 45°에 대해서 고려하여 Table 6과 같이 최종 case를 선정하였다. Solid 모델과의 정합성 비교를 위해 1Hz의 정현파 변위 5회 입력 이후의 최대 소성변형률 발생위치 및 값을 이용하였다⁽¹²⁾. 곡률에 따라 곡관의 강성이 다르기 때문에 적절한 수준의 소성변형을 발생시키기 위해 곡률에 따라 다른 수준으로 Table 7의 excitation과 같이 결정하였다. Surgeline의 구성 재료는 Table 9와 같이 SA 182 TP 316로, 가동온도 조건인 316 °C에서의 탄성계수 및 포아송비와 내부 유체를 added mass로 고려한 밀도를 적용하였다. 또한 배관 내부 유체에 의해 고유진동수 분리효과가 발생하는데, 내부 유체의 질량을 배관에 added mass 로 고려하여 분리된 고유진동수 중 구조물이 지배적인 모드만을 고려하였다^(12,13). 구속조건은 입력부 입력 변위를 제외한 모든 변위 구속, in-plane 방향의 회전을 제외한 모든 회전 구속, 지지된 부분 에서는 모든 변위 구속 및 in-plane 회전을 제외한 모든 회전 구속으로 설정하여 곡관의 개폐에 따른 영향을 확인할 수 있도록 하였다.

Fig. 10

Case study pipe elbow geometry

Table 6

Pipe size/Sch nominal sizes[mm]

Table 7

Pipe size/sch nominal sizes[mm]

Table 8

Information of case study model

Table 9

Case modal analysis result

구축한 solid 및 beam 모델의 모달 해석 결과 1차 모드 형상은 in-plane이 지배적인 형상으로, Table 9와 같이 동등한 결과가 도출되었다. 따라서 두 모델의 강성효과 및 동특성이 동일하다는 것을 확인하였다. 정현파 입력을 이용한 탄소성 해석 결과, Tables10~12와 같이 모든 case에서 기준 solid 모델 해석과 최대 소성변형이 나타나는 위치가 같고, 누적 소성변형률 값은 5.61 %~11.43 %의 차이를 가졌다. 상대적으로 단면의 강성이 낮은 배관계에서는 배관 측면 crown 부위에서 최대 소성이 나타나는 것을 확인하였고, 두꺼운 배관에서는 intrados 부분에서 최대 소성이 발생하는 동일한 경향성이 나타나는 것을 검증하였다. 이는 배관 파손을 유발하는 지배적인 모드의 차이에 기인한 것인데, 두껍고 곡관 부위의 강성이 높아 단면의 변형이 잘 생기지 않는 경우에는 입력 방향인 in-plane 방향으로의 변위에 의해 곡관 내면부에 압축으로 인한 응력집중이 발생하고, 최대 누적 소성변형이 발생하게 된다. 반면 곡관부위의 강성이 낮은 경우, ovalization 효과와 wrapping 효과가 단면의 변형을 유발하는 지배적인 모드가 되어 곡관 측면부에 응력집중 및 최대누적 소성변형효과가 발생하는 것을 알 수 있었다. 해당 결과는 solid 요소에 비해 elbow 요소를 적용한 beam 모델 결과가 높은 값을 도출하였는데, 이는 JSME 실험을 모사한 결과와는 상이한 경향성이다. JSME 배관의 경우 두께비 16.8의 얇은 배관으로 8 이상의 Fourier expansion number가 필요하다는 것을 의미한다. 또한 배관이 두꺼워짐에 따라 곡관의 변형 모드가 변하고, 이에 대해 적당 수준의 expansion number가 적용될 수 있다는 가능성을 제시한다. 이 연구에서는 2.2절 분석 결과 제시된 elbow요소의 변수 설정으로 서로 다른 형상을 갖는 배관에 대해 기준 solid 모델과 동일한 변형 지배 모드 구분이 가능했고, 적절한 수준의 취약부위 응답이 확인되기 때문에, 2.4절 배관계 동해석에 적용하여 동일한 응답 검증을 통해 활용 가능성을 확인했다.

Table 10

90° elbow case study result

Table 11

45° elbow case study result

Table 12

Case critical location comparison

2.4 Surgeline 배관계 탄소성 해석

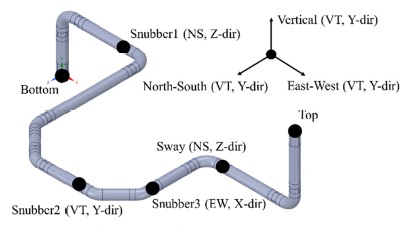
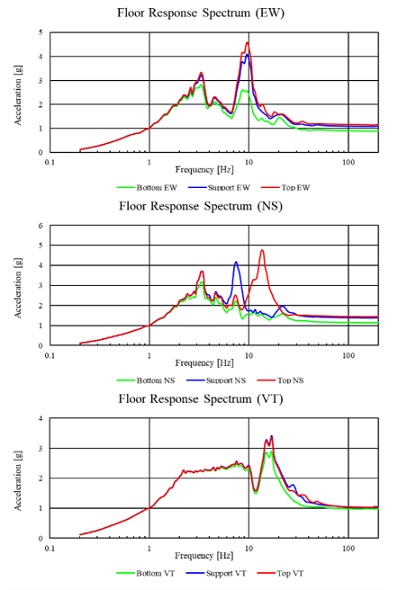
2.3절에서 곡관 요소 case study를 통해 활용 가능성을 확인했기 때문에 surgeline 배관계 동해석에 적용하여 응답 차이를 확인했다. surgeline 배관계의 형상은 Fig. 11과 같이, top 부분은 가압기기와 연결되어있고, bottom 부분은 주배관에 연결되는 노즐과의 연결되어 있다. 가압기와 주배관 노즐이 상대적으로 강성 및 질량효과가 크기 때문에 회전 변위는 고정된 것으로 간주하고 다음 부분에 3축 변위 입력을 적용하였다. 또한 4개의 지지대가 존재하는데, snubber 및 sway는 한 방향의 작동 방향의 변위를 지지하는 역할을 하므로 한 방향의 변위 입력에 대한 영향만을 고려했다. 변위입력은 Fig. 12의 작동 높이에 따른 원자력발전소 건물의 층 응답 스펙트럼을 이용하여 제작된 인공지진파를 소성변형을 일으킬 정도로 5 g 수준으로 증폭하여 사용하였다. 감쇠는 1차 고유진동수와 50Hz의 cut-off frequency를 갖는 4 % Rayleigh damping을 이용하였다⁽¹⁴⁾. 이는 JSME benchmark 프로그램과는 달리, 이 해석에서 이용한 응답스펙트럼의 개형이 다르기 때문에 높은 응답이 나타나는 주파수 구간을 고려해야하기 때문에 다른 cut-off frequency를 적용하였다.

Fig. 11

Surgeline geometry and boundary condition

Fig. 12

Floor response spectrum

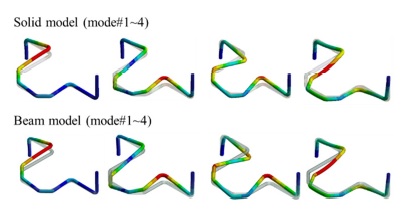
구축한 solid, beam 모델의 모달 해석을 진행하여 경계조건, 질량, 강성 구현의 적합성을 확인하였다. 모달 해석을 진행한 결과, Table 13과 같이 cut-off frequency 내에서 Fig. 13과 같이 동특성이 동일하기 때문에 두 모델의 질량, 강성, 경계조건이 동등하게 모델링 되었다는 것을 검증하였다. 구축된 모델을 이용하여 시간이력해석 결과 Fig. 14와 같이 동일한 곡관에서 최대누적 소성변형이 나타나고, 취약부위도 동일하게 intrados 위치에서 나타났다. 누적 소성변형률 값은 Table 14과 같이 26 %의 차이를 보였다. 반면 최대등가응력값은 같은 시간대에서 4.8 % 정도의 차이를 보이며 정확한 결과가 도출되는 것을 확인했다. 따라서 beam 요소를 이용한 배관계 동해석을 통해 취약부위 확인 및 응력 값 확인이 가능하다. 반면 누적 소성변형률 기준 26 %의 정확성은 JSME benchmark 프로그램에서 제시했던 기관별 해석 값 수용범위인 30 % 범위에 존재하기 때문에 정합한 결과로 볼 수 있다.

Table 13

Surgeline modal analysis result

Fig. 13

Surgeline mode shape (solid vs. beam model)

Fig. 14

Maximum accumulated plastic strain plot

Table 14

Surgeline elasto-plastic seismic analysis result

3. 결 론

이 논문에서는 Fourier expansion number를 이용한 elbow 요소를 이용한 탄소성 해석 방법에 대하여 연구하였다. JSME 실험을 모사한 solid 모델을 이용한 최적의 요소 변수 선정과 일반성 확보를 위한 case study를 통한 응답의 유효성 평가를 진행한 결과, 모든 case에서 누적 소성변형률 기준 최대 11 %의 값 차이를 보이며 동일한 취약부위를 확인할 수 있었고, 이는 지배적인 변형 모드가 동일하다는 것을 의미한다. 해당 설정을 surgeline 배관계에 적용하여 동해석 결과를 비교 검증한 결과 26 % 수준의 누적 소성변형률 차이와 4.8 % 수준의 최대 등가 응력 응답을 확인하였다. 이에 따라 이 연구에서 제시하는 탄소성 해석 방법론에 대한 결론을 정리하면 다음과 같다.

(1) Elbow 요소 및 Fourier expansion number를 적용하여 단면의 변형 모사효과를 고려한 유한요소해석이 가능하다.

(2) Fourier expansion number는 단면 변형의 자유도를 부여하는 역할을 하며 탄소성 해석에서 변형 지배 모드를 구분할 수 있게 한다.

(3) 요소 단위에서 case study 결과를 통해 곡관의 형상 특성에 따라 변형 지배 모드가 변하고, 최대 누적 소성변형이 발생하는 위치가 변하는 것을 확인하였고, elbow 요소를 이용하여 solid 모델과 동일한 변형 지배 모드 및 취약부위 확인이 가능하다.

(4) Surgeline 배관계 동해석에서도 elbow 요소를 이용하여 소성변형취약부위 선정이 가능하고, solid 요소를 이용한 경우와 동일한 등가응력응답이 도출된다.

(5) 원자력 발전소와 같이 구조물과 배관이 함께 존재하는 계의 탄소성 지진해석 시, elbow 요소를 이용하여 배관을 간략하게 모사 가능하고, 이를 통해 배관을 solid 요소로 모사한 경우와 유사한 소성변형률 확인 및 동일한 취약부위 확인이 가능하다.

이 논문에서는 배관이 가지는 구조적인 특성에 집중하여 동해석 모델을 구축하는 방법을 제시하였다. 해당 모델을 이용하여 배관의 거동에 대한 보다 정확한 해석을 위해서는 내부 유체에 의한 영향 및 온도조건을 고려하여 다양한 조건에 대한 활용성을 확보할 수 있을 것으로 기대된다.

Acknowledgments

이 연구는 2020년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다(No. 20193110100020, 해외 내진분석 기술기준을 적용한 표준형 원전 설계초과지진 대응 기술개발).

References

• Udagawa, M., Li, Y., Nishida, A. and Nakamura, I., 2018, Failure Behavior Analyses of Piping System under Dynamic Seismic Loading, International Journal of Pressure Vessels and Piping, Vol. 167, pp. 2~10. [https://doi.org/10.1016/j.ijpvp.2018.10.002]
• Kiran, A. R., Reddy, G. R., Agrawal, M. K., Raj, M. and Sajish, S. D., 2019, Ratcheting Based Seismic Performance Assessment of a Pressurized Piping System: Experiments and Analysis, International Journal of Pressure Vessels and Piping, Vol. 177, p. 103995. [https://doi.org/10.1016/j.ijpvp.2019.103995]
• Otani, A., Shibutani, T., Morishita, M., Nakamura, I., Watakabe, T. and Shiratori, M., 2017, Seismic Qualification of Piping System By Detailed Inelastic Response Analysis: Part2 - A Guideline For Piping Seismic Inelastic Response Analysis, Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, PVP2017-65190. [https://doi.org/10.1115/PVP2017-65190]
• Watakabe, T., Nakamura, I., Otani, A., Morishita, M., Shibutani, T. and Shiratori, M., 2017, Seismic Qualification of Piping System By Detailed Inelastic Response Analysis: Part4 - Second Round Benchmark Analyses With Stainless Steel Piping Component Test, Proceedings of the ASME 2017 Pressure Vessels and Piping Conference, PVP2017-65324. [https://doi.org/10.1115/PVP2017-65324]
• The American Society of Mechanical Engineers, 2015, Boiler and Pressure Vessel Code Section III Division 1 – Subsection NC, Rules for Construction of Nuclear Facility Components.
• Surh, H. B., Ryu, T. Y., Park, J. S., Ahn, E. W., Choi, C. S., Koo, J. C., Choi, J. B. and Kim, M. K., 2015, Seismic Response Analysis of a Piping System Subjected to Multiple Support Excitations in a Base Isolated NPP Building, Nuclear Engineering and Design, Vol. 292, pp. 283~295. [https://doi.org/10.1016/j.nucengdes.2015.06.013]
• Bathe, K. J. and Almeida, C. A., 1980, A Simple and Effective Pipe Elbow Element – Linear Analysis, Journal of Applied Mechanics, Vol. 47, No. 1, pp. 93~100. [https://doi.org/10.1115/1.3153645]
• Yan, A. M., Jospin, R. J. and Nguyen, D. H., 1999, An Enhanced Pipe Elbow Element – Application in Plastic Limit Analysis of Pipe Structures, International Journal for Numerical Methods in Engineering, Vol. 46, No. 3, pp. 409~431 [https://doi.org/10.1002/(SICI)1097-0207(19990930)46:3<409::AID-NME682>3.0.CO;2-N]
• Ansys® Academic Research Mechanical, Release 18.1, Help System, Coupled Field Analysis Guide, ANSYS, Inc.
• The American Society of Civil Engineers, 2005, Seismic Design Criteria for Structures, Systems, and Components in Nuclear Facilities.
• The American Society of Mechanical Engineers, 2018, Welded and Seamless Wrought Steel Pipe - B36.10M.
• Japan Society of Mechanical Engineers, 2019, “Codes for Nuclear Power Generation Facilities – Rules on Design and Construction for Nuclear Power Plant”.
• Lee, C. K., Lee, S. J., Lee, E. H. and Park, N. C., 2020, Methodology for Time History Analysis of Piping System Contains Internal Fluid Including Natural Frequency Separation Effect, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 2, pp. 112~118 [https://doi.org/10.5050/KSNVE.2020.30.2.112]
• U.S. Nuclear Regulatory Commission, 2007, Regulatory Guide 1.61-Damping Values For Seismic Design of Nuclear Power Plants.