물리기반 인공신경망을 활용한 리튬이온 전지 열화 예측
‡ Recommended by Editor Nam Keun Kim
© The Korean Society for Noise and Vibration Engineering
Abstract
Currently, lithium-ion batteries are becoming the most promising power source for a variety of portable electronics as well as electric vehicles. Some of the advantages that promote their widespread usage include their long battery cycle life, high durability, low self-discharge rate, and fast charge rate. However, despite their superiority in comparison with other power sources, there exists a lack of understanding regarding their battery lifetime owing to their sophisticated electrochemical actions, which cannot be sufficiently modeled and predicted using traditional physics-based models. This limitation has motivated the development of numerous data-driven approaches. However, data-driven methods also have certain limitations, such as low interpretability and inability to extrapolate well. This necessitates an alternative method that can leverage the strengths of both models while complementing their drawbacks. In this study, the state-of-health of lithium-ion batteries is estimated using a physics-informed neural network with the integration of physics in the deep learning pipeline. The results of this study indicate that the proposed model outperforms the conventional data-driven methods in RMSE and physical inconsistency.
Keywords:
Physics-informed Neural Network, Physical Inconsistency, Capacity Degradation, End-of-life, Model-based Method, Remaining Useful Life키워드:
물리기반 인공신경망, 물리적 불일치성, 용량 열화, 수명, 모델기반 방식, 잔존유효수명1. 서 론
리튬 이온 배터리는 최근 스마트폰, 디지털카메라, 전기자동차 등의 각종 전자기기에 가장 널리 활용되는 필수적인 에너지 공급원이다. 리튬 이온 배터리는 긴 수명, 높은 내구성 및 안정성, 낮은 자기방전율 그리고 빠른 충전 속도 등의 장점이 존재한다(1). 이러한 이점들로 인해 리튬 이온 배터리는 널리보급되고 있지만 배터리의 수명에 대한 이해는 환경과 사용조건에 따른 복잡한 전기화학적 작용으로 인해 매우 난해하며 수명 예측이 어렵다. 따라서 제품 설계 단계에서의 배터리의 열화 및 수명감소에 대한 정확한 유지보수 계획을 설정하지 못하여, 시설 유지 및 보수 비용이 증가하게 되는 경우가 발생한다. 하지만 수명 예측을 하기 위해서는 현 상태에서의 정확한 용량 예측이 우선 수반되어야 한다(2).
배터리 용량 예측에는 크게 물리모델 기반 접근방법과 데이터 기반 접근방법이 존재한다(3). 하지만 각각의 접근방법이 장·단점이 존재하기 때문에, 각 기법의 장점만을 융합한 하이브리드형 모델이 각광받고 있는 상황이다. 이 연구에서는 이런 추세에 따라 물리모델과 데이터를 동시에 활용하는 딥러닝 모델인 물리기반 인공신경망을 학습하여 배터리 수명 및 용량 예측을 하였다. 구체적으로, 사이클의 변화에 따라 배터리의 용량을 나타내는 상미분방정식을 심층신경망 학습에 사용되는 목적 함수에 추가하여 심층신경망 변수 학습 시 지도 가능하도록 설계하였다. 이 연구에서 제안하는 예측 결과는 데이터 기반 모델의 대표적인 심층신경망인 순환신경망(recurrent neural network, RNN) 및 인공신경망(artificial neural network, ANN)과 비교를 하여 제안 모델의 우월성을 검증하였다. 이 방법론 배터리의 가장 대표적인 상태 지표인 수명(state of health, SoH)를 실시간으로 보다 정확하게 예측할 수 있다는 장점이 존재한다.
2. 리튬이온 배터리 SoH 모니터링
2.1 State-of-health (SoH)
리튬이온 배터리와 관련된 연구 중에서 가장 필수적인 분야 중 하나는 배터리의 상태 또는 건전성 예측이다. 배터리가 실생활에 없어서는 안 될 필수품으로 자리를 잡으며 여러 분야에서 매일 사용되기 때문에 안정성과 경제성 등을 충족시키기 위해 충전을 해야 할 시기와 정비를 해야 할 시기 등을 미리 예측할 수 있어야 하기 때문이다. 하지만 배터리의 상태는 양극, 음극에 도포된 활물질에 리튬이온이 삽입되는 난해한 전기화학 메커니즘에 좌우되기 때문에 수명예측이 난해하다. 또한 수명은 방전깊이(depth-of-discharge, DoD), 온도 등에 의존적이기 때문에 운전조건에 대한 규명 또한 필수적이다. 더불어 배터리의 수명 지표를 무엇으로 정해야 하는지도 명확하지 않다.
배터리의 수명 지표에는 크게 용량, 내부저항 그리고 자기방전(self-discharge) 등이 존재하지만 최근에는 용량을 많이 대표적인 지표로 고려하는 추세이다. 배터리의 용량을 나타내는 정량적 지표는 크게 두 가지 종류로 나눌 수 있다. 하나는 잔존용량(state-of-charge, SoC)이며 다른 하나가 바로 SoH이다(4). SoC와 SoH의 차이는 영구적인 용량손실의 포함 여부이다. 예를 들어, 평소에 확인하는 휴대폰의 배터리 잔량이 바로 SoC에 해당한다. 하지만 SoC는 배터리 열화에 기인한 영구적 용량손실을 고려하지 않는다. 따라서 SoC는 완전 충전할 때마다 100 %를 채울 수 있지만, 열화에 의하여 배터리 충전가능한 총 용량이 지속적으로 감소되기 때문에 정확한 사용 가능한 잔량이라고 간주하기 어렵다. 따라서 배터리의 수명을 나타내는 정확한 지표는 SoH이며, 열화에 기인한 영구적 용량손실을 고려하는 개념이기에 설계치 또는 공장에서 제조된 바로 직후건전한 배터리만 100 %이며 시간이 지날수록 최대치가 낮아지게 된다. 전기자동차에서는 설계치 또는 건전한 배터리 용량의 80 %를 설계수명(end-of-life, EoL)로 정의하며 이를 기반으로 전기자동차에 사용되는 리튬이온 배터리팩을 교체, 파기 또는 재활용 한다. 구체적인 SoH의 수학적 정의는 식 (1)과 같다(5).
| (1) |
여기서 Cn은 영구적 손실분량을 포함한 배터리의 설계 용량을 뜻하며, Co는 영구적 손실분량을 제외한 용량수치를 의미한다. 따라서 배터리의 충전과 방전을 반복하고 시간이 지날수록 상술한 다양한 열화인자에 의하여 Co는 감소하지만 Cn는 설계용량이기 때문에 일정하다.
2.2 리튬이온 배터리 데이터
수명 예측 관련 연구를 수행하기 위해서 제일 힘든 작업 중 하나가 다양한 환경조건에서 수명관련 데이터베이스를 구축하는 일이다. 특히 배터리의 경우 상술한 다양한 환경조건을 고려하여 수명 관련 데이터 베이스를 구축하는 것은, 급속 충전 및 방전을 여러 번 반복하여 EoL까지 도달 할 수 있는 가속 열화시험을 수행할지라도 짧으면 수개월에서 길면 몇 년이 걸린다. 이러한 데이터 취득의 경제성 문제를 고려하여, 이 연구에서 제안하는 방법론의 적용타당성 분석을 위해 실제 실험을 기반으로 한 공개 데이터셋을 구하여 사용하였다. 구체적으로, 활용된 데이터는 2019년에 Nature Energy 저널에 처음 소개된 데이터셋으로 현재 공개된 리튬이온 배터리 데이터 중 가장 규모가 크다(6). 현재 상용품인 124개의 인산철/흑연(LFP/graphite) 배터리로 가속열화시험을 통해 취득한 데이터이며 명시된 용량의 최대치는 1.1 Ah이다. SoC를 0 %에서 80 %까지 충전할 시에는 72가지의 서로 다른 한 단계 및 다단계 충전 프로토콜을 통해 급속 충전을 하였으며 나머지 100 %까지의 충전은 균일한 1C의 정전류-정전압(constant current-constant voltage, CC-CV) 조건에서 3.6 V까지 진행되었다. 방전은 모든 배터리에 대해 동일하게 4C의 CC-CV 조건에서 2.0 V까지 진행되었다. 이러한 다양한 조건의 실험을 통해 150에서 2300 사이클에 해당하는 다른 열화 데이터베이스를 구축하였으며, 각 배터리에 대하여 사이클에 따른 방전용량(discharge cycle)을 추정 가능하다. 해당 논문에서는 124개의 배터리 중 41개를 학습 데이터, 43개를 검증 데이터 그리고 나머지 40개를 테스트 데이터로 구분하여 모델을 학습, 최적화 및 검증을 하였다. 배터리 당 데이터의 수는 150개~2400개로 배터리 별로 상이하다. 이 연구에서도 이를 동일하게 사용하였다.
2.3 SoH 측정 물리 모델
리튬이온 배터리의 용량 혹은 SoH를 예측하는 모델은 무수히 많이 존재한다. 이 연구에서는 추후에 자세히 소개될 물리기반 인공신경망에 적합한 물리 모델식을 사용하였고 이는 식 (2), (3)과 같이 정의된다(7).
| (2) |
| (3) |
식 (2)는 사이클 N에 따른 배터리 수명 L을 나타내며 초기 음극에 발생하는 고체 전해질 계면(solid electrolyte interphase, SEI) 필름 생성과 현 수명 상태에 의존하는 배터리 수명 특성으로 인한 비선형성을 나타내고 있다. 여러 실험을 통해 배터리의 열화 속도는 가장 초기 및 EoL에 도달하기 전에 가장 빠르다는 점을 반영하고 있다. αsei는 SEI 필름 생성에 소비된 용량의 분율을 나타내며 βsei는 반복된 사이클 및 온도가 필름 생성에 미치는 영향을 반영한 파라미터이다. 또한 식 (3)은 배터리의 열화와 연관된 여러 요인들과 그들 간의 관계성을 나타낸다. 열화 요인을 크게 네 가지로 나눌 수 있으며, 왼쪽부터 순서대로 DoD 응력 모델, 시간 응력 모델, SoC 응력 모델 그리고 마지막으로 온도 응력 모델로 구성되어 있다. 각 응력 모델과 관련된 파라미터들은 kδ, e1, kδ, e2, kt, kσ, kT이며 시간 응력을 제외한 나머지는 모두 지수 함수적으로 증가한다. 또한 t, δ, σ, T는 사이클에 따른 시간, DoD, SoC 그리고 온도를 나타낸다. 이 중에서 DoD 응력 모델과 시간 응력 모델은 서로 더한 값을 나머지 요인들에 곱하여 얻게 되는데 이는 이론 및 실험을 통해 얻은 반 경험적 모델(semi-empirical model)이다. 이 연구에서는 위 모델식을 일반적인 인공신경망에 통합시켜 물리기반 인공신경망을 학습하였고 초기 파라미터는 2.2절에서 소개된 학습용 데이터에 곡선 적합을 통해 정하였다.
2.4 물리기반 인공신경망
물리기반 인공신경망(physics-informed neural network, PINN)이란 기존의 딥러닝에서 자주 활용되는 심층신경망에 일종의 사전 지식이라고 할 수 있는 지배방정식 또는 물리법칙 등을 통합시켜 학습의 속도, 정확성 그리고 물리적 불일치성을 최소화시키는 기법이다(8~10). 이는 배터리 수명 및 용량 예측에 있어서 전통적으로 활용되는 모델기반 방식과 데이터기반 방식을 융합하여 서로의 단점을 보완하기 위해 개발되었다.
모델기반 방식의 경우 입력 변수와 출력 변수 간의 매우 복잡한 관계식을 충분히 추정하기 어려우며, 지배방정식에 모사된 응답만을 도출 가능하다는 단점이 존재한다. 반대로, 데이터기반 방식은 데이터의 오차와 편향을 그대로 학습할 가능성이 있으며 이로 인해 발생하는 물리적 불일치성과 결과에 대한 물리적 관점에서의 해석이 어렵다는 단점이 존재한다. 또한 심층신경망을 학습시키기 위한 방대한 데이터가 필요하다는 한계를 갖는다. 반면, 물리기반 인공신경망은 각 접근방법의 장점을 독려하는 반면, 단점을 서로 상쇄시킬 수 있다.
기존의 여러 인공신경망에 사전 지식을 주입시키는 방법에는 여러 가지가 존재한다(11). 이에 대한 방법론은 크게 세 가지 종류로 분류할 수 있다. 첫째로는 학습용 데이터 자체를 사전 지식을 통해 가공하는 방식(physics-based preprocessing)이다. 이는 가정 널리 활용되는 방법으로서 기존의 딥러닝 방식에서도 성능 향상을 위해 자주 사용되었다. 특히 기존의 물리기반 모델의 결과값을 학습용 데이터에 추가하는 방법은 성능 향상에 효과적으로 알려져 있다. 두 번째 방식은 심층신경망의 구조를 물리적 지식에 맞추어 설계하는 것(physics-based network architecture)이다. 이에 대한 예시로는 상미분방정식을 이산적인 관점에서 해석하여 시간에 따른 증가분을 딥러닝의 대표적 시계열 분석 모델인 RNN 셀로 하여금 모델링 하는 방법이 있다. 마지막 방식에는 모델의 전체적인 학습 지도에 있어 사전 지식을 주입하는 방법(physics-based regularization)이 있다. 대다수의 딥러닝 모델은 파라미터 최적화 시 두 가지의 목적 함수(empirical loss 및 regularizer)를 최소화시킨다. 이 방식은 이러한 기존 목적 함수에 물리적 지배방정식을 추가시켜 최적화 유도한다. 이 연구에서는 활용 방식이 단순함에도 학습효과가 높은 마지막 방식을 사용하였다.
2.5 모델 학습 및 실험 설계
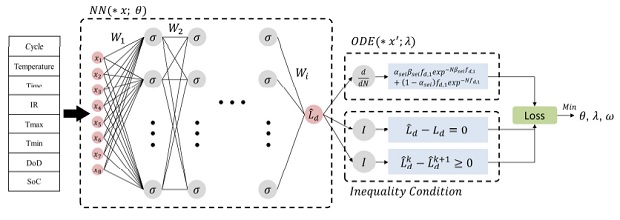
2.2절에 소개된 공개 열화데이터의 입력 변수는 사이클, 온도, 최고 온도, 최저 온도, 시간, DoD, SoC, 내부 저항이 있다. 이에 따라 심층신경망의 구조는 Table 1과 같다. 은닉층의 구조는 여러 사전실험을 통해 시행착오법을 이용하여 도출하였으며, 추후 다양한 최적화 기법의 적용을 통하여 최적화를 수행할 예정이다. 출력단은 하나의 노드가 존재하며 이는 배터리의 수명을 도시한다.
해당 인공신경망의 목적 함수는 세 가지가 존재하며 Fig. 1에 도시하였다. 왼쪽에는 Table 1 구조의 일반적인 인공신경망이 자리하고 있다. 이에 대한 목적 함수는 오른쪽 부분에 도시하였다. 최상단의 목적 함수는 식 (2) 상미분방정식으로 표현되는 배터리 수명 모델이다. 이것이 물리기반 목적 함수의 한 가지 형태이다. 애초에 상미분방정식이 사이클에 대한 미분 형태이기 때문에 인공신경망의 출력단에 나온 값을 사이클에 대해 미분을 적용하여 식에 대입해야 한다. 중간에 위치해 있는 목적 함수가 학습용 데이터를 적합하기 위한 것이며 예측한 값이 실제 값과 최대한 동일해야 함을 나타내고 있다. 이에는 일반적인 평균제곱오차(mean squared error, MSE) 함수가 사용되었다. 최하단의 목적 함수는 물리 법칙을 표현한다. 이는 이전 사이클에서 예측한 배터리 수명은 이후 사이클에서 예측한 값보다는 크거나 같아야 한다는 물리적 법칙을 의미한다. 수명은 과전위(overpotential)가 존재하지 않는 한 사이클이 지날수록 감소하기 때문이다. 해당 목적 함수는 인공신경망의 출력단에서의 예측값을 그대로 가져와 대입한다.
세 가지의 목적 함수에서 출력되는 값들을 모두 더해서 이를 최소화시키는데 이때 학습되는 파라미터는 인공신경망 파라미터(θ), 물리모델 파라미터(λ) 그리고 목적 함수간의 가중치(ω)이다. Table 2는 해당 모델의 여러 가지 하이퍼 파라미터를 보여준다. 모델을 학습할 때는 2.2절에서 소개된 학습 데이터로 검증 데이터에 대하여 모델 최적화를 하며 최종적으로는 테스트 데이터에 대하여 검증을 진행하였다.
추가적으로, 실험 설계는 물리기반 인공신경망의 우수성을 증명하기 위해 동일한 조건에서 RNN의 일종인 장단기 메모리(long short-term memory, LSTM) 및 ANN과 비교를 하였으며 구조는 ANN의 경우 PINN의 구조와 동일하며 LSTM은 입력단 [8], 은닉층 [10 × 2] 그리고 출력단 [1]으로 구성하였다. 또한 나머지 하이퍼 파라미터는 기본 설정을 사용하였다. 모델 평가 지표는 평균 제곱근 오차(root mean squared error, RMSE)와 물리적 불일치성(physical inconsistency, PI)를 사용하였다. 또한 물리기반 목적 함수의 존재로 인해 적은 수의 학습용 데이터로 최적화가 잘 되는지에 대한 고찰을 하였다.
2.6 결과 및 분석
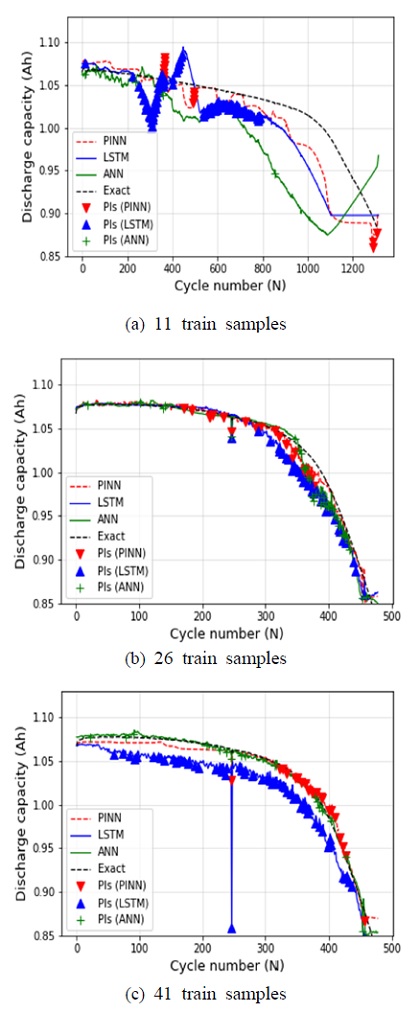
Fig. 2는 위에서부터 차례로 학습용 데이터의 개수가 11, 26 그리고 41일 때의 용량 예측 결과를 보여주고 있다. 학습용 데이터가 11일 때의 용량 예측을 보면 매우 적은 학습 데이터 수로 인해 그 어느 모델도 예측이 잘 안 되는 것을 확인할 수 있다. 다만 세 가지의 비교 모델 중 물리기반 인공신경망 이 가장 실험값에 근접함을 알 수 있다. 또한 물리적 불일치성에 대한 개수는 10개로 11개의 ANN 보다는 살짝 적게 나왔지만 53개의 LSTM과 비교해서는 매우 적은 수치이다. 학습 데이터의 수가 26과 41일 때의 결과는 거의 비슷하다. 이때는 데이터의 개수가 충분하여 세 가지 모델 모두 실제와 매우 근접하게 예측하고 있지만 물리기반 인공신경망이 가장 근접하며 PI의 개수도 19, 17개로 각각 26, 23개의 ANN과 32, 45개의 LSTM에 비해 상대적으로 적다. PI를 세는 기준은 사이클이 지남에 따라서 예측되는 용량의 수치가 이전 사이클에서의 수치보다 일정 수준 이상 큰 경우로 정한다.
이로써 물리기반 인공신경망은 동일 조건에서 다른 일반적인 딥러닝 모델보다 더 적은 수의 학습 데이터로 향상된 예측 성능을 보인다는 것을 알 수 있었다. 이는 현실적으로 데이터를 취득하기 어려운 여러 분야에 의미 있는 결과로 사료된다.
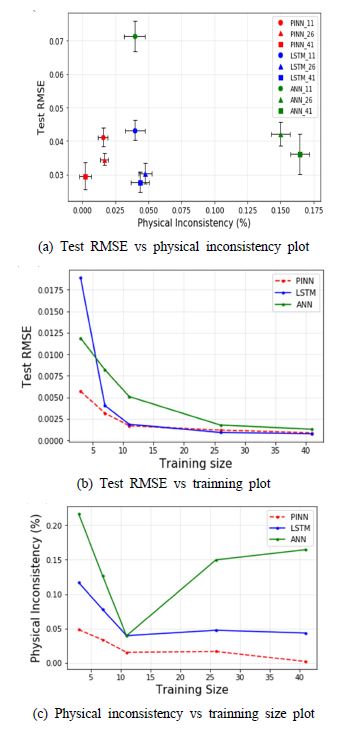
Fig. 3은 여러 조건에서의 실험 결과를 정리해놓은 그래프이다. Fig. 3(a)는 물리적 불일치성에 대한 RMSE 그래프이며 Fig. 3(b)는 학습 데이터의 개수에 따른 RMSE 그리고 Fig. 3(c)는 학습 데이터의 개수에 따른 물리적 불일치성을 나타낸다.
Fig. 3(a)에서 확인할 수 있는 점은 물리기반 인공신경망에 대한 결과값이 학습 데이터의 개수에 관계없이 그래프에서 하단의 가장 좌측에 몰려있는 것이다. 또한 이 결과를 통해 확인할 수 있는 점은 특정 구간부터는 RMSE로 도시된 오차가 LSTM이 물리기반 인공신경망보다 높다는 점이다. 이를 해석하자면 LSTM의 경우 RNN 계열의 모델로서 일반적으로 더 많은 수의 학습 파라미터를 지니고 있으며 높은 수준의 예측 성능을 위해서는 굉장히 많은 수의 데이터를 요구하기에 학습 데이터의 개수가 낮은 지점에서는 ANN 계열의 물리기반 인공신경망보다 낮게 나올 수가 있다. 따라서 데이터가 충분히 주어지고 시간에 따라 변화하는 데이터를 다루는 경우 LSTM이 더 잘 작동하게 되는 것이다.
그럼에도 불구하고 물리적 불일치성에 있어서는 그 어느 경우에도 물리기반 인공신경망을 따라오지 못하는 것을 Fig. 3(c)에서 확인할 수 있다. Fig. 3(b)에서 주목해야 할 점은 학습 데이터가 충분히 없는 지점에서는 압도적으로 물리기반 인공신경망이 좋다는 것이다. 이러한 관찰결과는 데이터가 부족한 여러 분야에서 물리기반 인공신경망을 유용하게 활용할 수 있다는 점을 시사한다. 또한, 물리 모델식을 목적 함수에 추가하는 것은 regularizer로서의 역할을 충분히 하며 ANN과 같이 시간 관계성을 잘 파악하지 못하는 모델에 대해서도 사전 지식이 큰 도움이 되었다는 점을 추론 가능하다. 위의 결과에 따라 향후 연구 방향으로 사전 지식을 ANN이 아닌 RNN 계열에 접목시켜 성능을 높이는 방식과 이에 따라 RNN 계열임에도 상대적으로 적은 수의 데이터로도 좋은 성능이 나오는지를 확인하여 해당 방법론이 실용적으로 적용 가능한지에 대한 부분을 연구해야 할 것으로 보인다.
3. 결 론
이 연구에서는 기존의 딥러닝 모델에 사전 지식을 접목시킨 물리기반 인공신경망을 사용하여 리튬이온 배터리의 SoH 예측을 진행하였다. 리튬이온 배터리의 SoH를 예측하는 작업에는 전통적으로 크게 모델기반 방식과 데이터기반 방식으로 나뉜다. 하지만 각 방식은 단점이 존재하며 이를 서로 보완할 수 있는 하이브리드 형식의 모델이 각광받는 추세이다. 하이브리드 형식의 모델은 모델기반 방식의 복잡한 관계식을 모델링하지 못하는 점과 데이터 기반 방식의 일반화 성능이 떨어진다는 점 등을 서로 보완할 수 있을 것으로 기대된다. 이 연구를 통해 심층신경망에 물리지식을 접목시켜 얻을 수 있는 이점에는 상대적으로 적은 수의 학습 데이터로 낮은 RMSE와 적은 수의 물리적 불일치성을 얻을 수 있다는 것으로 나타났다. 하지만 학습 데이터가 충분할 때는 LSTM과 비교해서 RMSE 측면에서 낮은 성능을 보이기에 이를 대체하기 위한 후속 연구가 필요하다. 추가적으로, 리튬이온 배터리의 경우 사이클에 따른 용량 모니터링도 중요하지만 이를 상태 지표로 활용하여 잔존유효수명(remaining useful life)을 예측하는 방향의 연구가 필요하다. 잔존 유효수명을 예측하는 모델식은 일반적으로 존재하지 않기 때문에 이런 경우에도 물리기반 인공신경망으로 예측이 가능한지도 분석이 필요하다. 그럼에도 불구하고, 기존의 딥러닝에 대해서는 여러 한계점이 존재하기에 이를 대체하기 위한 후속 연구가 필요할 전망이며 물리기반 인공신경망이 이러한 대안 중 하나가 될 것으로 사료된다.
기 호 설 명
| Cn : | 배터리 최대치 용량 |
| Co : | 영구 손실분을 제외한 용량 |
| C : | 방전율 |
| L : | 배터리 수명 |
| N : | 사이클 |
| fd,1 : | 한 사이클 당 줄어든 수명 |
| θ : | 인공신경망 학습 파라미터 |
| ⋋ : | 물리모델 파라미터 |
| ω : | 목적 함수 간 가중치 |
Acknowledgments
이 연구는 정부 (과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2020R1A2C1009744), 2019년도 정부(산업통상자원부)의 재원으로 한국산업기술진흥원의 지원을 받아 수행된 연구임(P0008691, 2019년 산업전문인력역량강화사업), 2021년도 정부(과학기술정보통신부)의 재원으로 정보통신기획평가원의 지원 받아 수행된 연구임(No.2019-0-01906, 인공지능대학원지원(포항공과대학교)).
References
-
Barré, A., Deguilhem, B., Grolleau, S., Gérard, M., Suard, F. and Riu, D., 2013, A Review on Lithium-Ion Battery Ageing Mechanisms and Estimations for Automotive Applications, Journal of Power Sources, Vol. 241, pp. 680~689.
[https://doi.org/10.1016/j.jpowsour.2013.05.040]

- Kwon, D., Kim, J. H., Park, G., Bae, S. J., An, D. et al., 2016, Recent Trends in the Research of PHM Techniques, Proceedings of the KSNVE Annual Autumn Conference, p. 124.
-
Zhou, D., Li, Z., Zhu, J., Zhang, H. and Hou, L., 2020, State of Health Monitoring and Remaining Useful Life Prediction of Lithium-Ion Batteries Based on Temporal Convolutional Network, IEEE Access, Vol. 8, pp. 53307~53320.
[https://doi.org/10.1109/ACCESS.2020.2981261]

-
Zou, Y., Hu, X., Ma, H. and Li, S. E., 2015, Combined State of Charge and State of Health Estimation over Lithium-Ion Battery Cell Cycle Lifespan for Electric Vehicles, Journal of Power Sources, Vol. 273, pp. 793~803.
[https://doi.org/10.1016/j.jpowsour.2014.09.146]

- He, L. and Shin, K. G., 2017, How Long Will My Phone Battery Last?, arXiv preprint arXiv:1711.03651, .
-
Severson, K. A., Attia, P. M., Jin, N., Perkins, N., Jiang, B. et al., 2019, Data-driven Prediction of Battery Cycle Life before Capacity Degradation, Nature Energy, Vol. 4, No. 5, pp. 383~391.
[https://doi.org/10.1038/s41560-019-0356-8]

-
Xu, B., Oudalov, A., Ulbig, A., Andersson, G. and Kirschen, D. S., 2016, Modeling of Lithium-ion Battery Degradation for Cell Life Assessment, IEEE Transactions on Smart Grid, Vol. 9, No. 2, pp. 1131~1140.
[https://doi.org/10.1109/TSG.2016.2578950]

- Von Rueden, L., Mayer, S., Beckh, K., Georgiev, B., Giesselbach, S. et al., 2019, Informed Machine Learning-A Taxonomy and Survey of Integrating Knowledge Into Learning Systems, arXiv preprint arXiv:1903.12394, .
-
De Bezenac, E., Pajot, A. and Gallinari, P., 2019, Deep Learning for Physical Processes: Incorporating Prior Scientific Knowledge, Journal of Statistical Mechanics: Theory and Experiment, Vol. 2019, No. 12, p. 124009.
[https://doi.org/10.1088/1742-5468/ab3195]

- Karpatne, A., Watkins, W., Read, J. and Kumar, V., 2017, Physics-guided Neural Networks (PGNN): An Application in Lake Temperature Modeling, arXiv preprint arXiv:1710.11431, .
-
Rai, R. and Sahu, C. K., 2020, Driven by Data or Derived Through Physics? A Review of Hybrid Physics Guided Machine Learning Techniques With Cyber-Physical System (CPS) Focus, IEEE Access, Vol. 8, pp. 71050~71073.
[https://doi.org/10.1109/ACCESS.2020.2987324]


Sung Wook Kim received a B.S. degree from Hanyang University, Seoul, South Korea, in 2016. He then received his M.S. degree in Mechanical Engineering from Pohang University of Science and Technology, Pohang, South Korea, in 2018. He is now a Ph.D. candidate at the Industrial AI Lab. of Pohang University of Science and Technology.

Ki-Yong Oh received his B.S. degree in Mechanical Engineering from Hanyang University, Seoul, Korea, in 2005, M.S. degree in Mechanical Engineering from KAIST in 2006, and Ph.D. in Mechanical Engineering from University of Michigan, Ann Arbor, in 2016. He joined the School of Energy System Engineering at the Chung-Ang University in 2017, where he is currently employed as an assistant professor. Dr. Oh’s teaching and research interests include applied dynamics, and prognostics and health management in the field of complex energy systems

Seungchul Lee received a B.S. degree from Seoul National University in 2001. He then received his M.S. and Ph.D. degrees from the University of Michigan, Ann Arbor, USA, in 2008, and 2010, respectively. He was an assistant professor with the Ulsan National Institute of Science and Technology, South Korea. He is currently an assistant professor at the department of mechanical engineering at Pohang University of Science and Technology in Pohang, South Korea, since 2018. His research interests include industrial artificial intelligence with mechanical systems, deep learning for machine healthcare, and the IoT-based smart manufacturing.