헬리컬 기어의 3차원 진동 해석을 위한 동역학 모델 개발

1. 서 론

기어의 동적 거동을 이해하고 분석하는 것은 기어 시스템(기어-샤프트-베어링)의 소음과 내구 성능을 만족시키기 위한 설계에 있어 필수적이다. 일반적으로 기어 시스템에서 진동은 기어의 정적 전달오차(static transmission error, STE)가 가진력으로 작용하여 발생한다. 동적 상태에서 STE가 공진점 부근에서 증폭이 되어 매우 큰 전달오차를 유발시키고 이것을 흔히 동적 전달오차(dynamic transmission error, DTE)라고 한다. DTE가 결국 기어 시스템에 동적 부하 및 응력을 가중시켜 기어 뿐만 아니라 샤프트, 베어링 등의 피로 내구 수명을 감소시키는 주요 원인이 된다. 더욱이 동적 상태에서 기어의 high frequency mesh force가 샤프트와 베어링을 통해 기어 박스 하우징에 전달되어 structure-bone 기어 와인 노이즈를 유발시킨다. 따라서 기어박스 설계에서 소음과 내구 수명을 만족시키기 위해 기어 진동을 줄이는 연구가 많이 진행되고 있다. 이러한 측면에서 헬리컬 기어가 스퍼 기어 보다 더욱 선호되고 있으며 자동차, 항공, 및 풍력발전 등 기계 산업 전반에 걸쳐 광범위하게 사용되고 있다. 보통 스퍼 기어는 강한 비선형 특성으로 인해 DTE 크기가 아주 큰 것으로 알려져 있다^(1~4). 반면에 헬리컬 기어는 STE가 작고 기어 mesh stiffness의 변동량이 작아 결과적으로 DTE 크기가 스퍼 기어에 비해 월등히 작아 소음과 내구성 측면에서 유리하다. 그러나 헬리컬 기어는 스퍼 기어 보다 상대적으로 진동의 크기는 작으나 헬릭스 앵글(helix angle, β)로 인해 축력이 발생하여 베어링 타입과 용량 선정에 추가적인 노력이 필요하다. 또한 기어 mesh force의 축 방향 성분이 tilting moment를 유발시키고, 이를 지지하기 위해 추가적으로 기어 바디, 샤프트, 베어링에 더 큰 강성을 갖도록 설계해야하는 어려움이 존재한다. 다시 말해, 스퍼 기어 보다 진동량은 작지만 헬리컬 기어의 경우는 헬릭스 앵글로 인해 3차원 기어 진동을 모두 고려한 설계를 해야 함을 의미한다. 이러한 헬리컬 기어의 3차원적인 거동의 중요성에 대한 연구가 학계에 발표된 바가 있다^(5~14). Neriya, S. V. et al.⁽⁵⁾의 경우 헬리컬 기어는 각 torsional, flexural, rotational, 그리고 axial 방향으로 진동이 서로 커플링(coupling)되어 있음을 보여줬다. Kahraman, A.⁽⁶⁾는 헬리컬 기어의 coupling 모드 해석을 위해 샤프트와 베어링의 flexibility를 고려하였다. 이를 통해 축 방향의 진동 값을 예측하였다. Kubur, M. et al.⁽¹⁰⁾은 유한요소법을 적용한 샤프트 모델을 기어 동역학 모델과 접목하여 샤프트의 치수(길이)와 베어링 강성이 기어 진동에 미치는 영향을 연구하였다. Zhang⁽¹¹⁾은 헬리컬 기어 시스템의 수학적 모델을 고안하였다. 기어, 베어링, 샤프트의 강성을 고려하여 기어의 편심 오차가 헬리컬 기어의 동적 거동에 어떠한 영향을 미치는지 연구하였다. 또한, Zhang, H. et al.⁽¹²⁾은 원심 압축기(centrifugal compressor)의 회전체 시스템을 유한요소법을 이용한 동역학 모델을 제시하였다. 헬리컬 기어의 치 강성을 상수 값과 가변(time-varing) 값을 가질 때의 두 경우로 나누어 연구를 진행하였고, 각각의 경우에 대하여 베어링의 감쇠비가 시스템 진동에 미치는 영향에 초점을 맞추었다. Yan, M. et al.⁽¹³⁾은 Zhang, H. et al.^(11~12)의 기어 시스템 동역학 모델과 ANSYS 소프트웨어를 결합하여 헬리컬 기어의 동적 거동을 연구하였다. 기어 치의 상대 변위는 ANSYS 소프트웨어를 이용하여 계산하였고 그 값을 기어 해석 모델에 접목하여 기어의 3차원 진동 모델을 개발하였으며, 기존 연구^(10~12) 방법들과 Yan, M. et al.⁽¹³⁾이 개발한 모델의 해석 결과를 비교함으로서 해석 모델의 유효성을 간접적으로 보여주었다. 실험적 방법으로 Kang, M. et al.⁽¹⁴⁾은 가속도계를 이용한 기어시스템의 3차원 진동 계측 방법을 개발하여 헬리컬 기어 시스템에 적용하였다. 그 결과 헬리컬 기어의 진동은 torsional, transverse, rotational, 그리고 axial 방향으로 모두 커플링이 되어 있음을 실험적으로 보여주었다. 실험 결과를 통해 헬리컬 기어의 동역학 모델은 3차원에서 다뤄야 한다고 강조하고 있다.

해석 모델의 유효성 검증에 대한 연구는 Kubur, M. et al.⁽¹⁰⁾의 사례에서 찾아볼 수 있다. 모델 검증을 위해 가속도계를 이용하여 헬리컬 기어 시스템에 대한 DTE를 측정하였고 그 실험값을 기어의 3차원 진동 예측 모델의 해석 값과 비교함으로서 해석 모델의 유효성을 검증하였다. 그러나 이러한 비교는 기어 해석 모델의 torsional 방향의 진동 예측에 대한 유효성은 보여주었으나 transverse와 rotational 방향에서의 유효성을 보여주기에는 부족한 측면이 있다.

이상의 연구를 통해 헬리컬 기어의 3차원 동적 거동을 예측하기 위한 해석 모델에 대한 연구는 있지만 3차원 방향에서의 진동 예측값을 실험값과 비교하여 기어 동역학 해석 모델의 유효성을 검증한 사례는 아직까지 보고 되지 않았다. 따라서 이 연구는 헬리컬 기어의 3차원 진동 예측을 위한 동역학 모델을 개발하고 실험값과 비교함으로서 모델의 유효성을 검증하고자 한다. 또한 해석 모델에 적용된 가정이 효과적임을 보여주고자 한다. 이 연구에서는 기존 연구⁽¹⁴⁾에서 측정된 헬리컬 기어의 동적 특성이 선형적으로 거동한다는 결과를 참조하여 헬리컬 기어 시스템을 LTI(linear-time invariant) 시스템으로 간주하였다. 일반적으로 스퍼 기어는 기존 사례^(1~4)에서 보고된 바와 같이, 공진점 부근에서 공진 곡선의 discontinuity가 두드러지게 관찰된다. 이것은 기어 시스템의 대표적인 비선형 거동을 의미한다. 그러나 이러한 비선형 거동은 헬리컬 기어에서는 아주 드문 현상으로 헬리컬 기어 시스템은 일반적으로 선형성을 가진다고 알려져 있다^(6~14). 따라서 기어의 비선형 거동을 유발 시키는 백래쉬(backlash)는 이 연구에서는 고려하지 않았고 이와 같은 이유로 기어 치 강성 값을 상수인 선형 스프링으로 간주하였다.

헬리컬 기어 시스템에서 gyroscopic moment는 일부 공진점의 위치와 공진 크기에 아주 적은 영향을 미친다고 알려져 있다⁽¹⁵⁾. 따라서 이 연구에서는 기어 바디와 샤프트 모델은 오일러 빔 요소(Euler’s beam element)를 이용하였고 gyroscopic moment와 shear deformation은 고려하지 않았다. 또한, 베어링의 flexibility를 반영할 수 있도록 모델링하였다.

이 연구의 주요 특징으로, 기존 연구 Kubur, M. et al.⁽¹⁰⁾, Zhang, H. et al.^(11~12), Yan, M. et al.⁽¹³⁾에서는 기어 바디를 강체로 가정하여 lumped mass로 모델링을 하였으나, 이 연구에서는 기어 바디를 변형체로 간주하여 샤프트 요소와 같은 빔 요소로 모델링하였다. 이는 공진점 예측의 정확성을 높이기 위함이며 다음 장에 기존 연구와 그 차이점을 자세하게 소개하였다.

2. 해석 모델

2.1 헬리컬 기어 모델

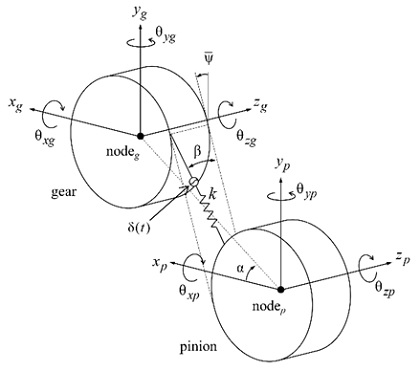
Fig. 1는 헬리컬 기어 쌍의 피니언(pinion, p)과 기어(gear, g)를 3차원적으로 모델링하는 방법을 보여주고 있다. 두 헬리컬 기어의 바디는 기어 접촉면의 법선 방향으로 선형 스프링 k를 이용하여 연결 된다고 가정한다. STE(δ(t))가 변위 가진원으로서 스프링과 같은 방향으로 연결되어 있고 기어의 상대 위치는 Fig. 1에서 보는 바와 같이 α와 $$ \overline{\mathrm{\psi }}$$로 정의할 수 있다. 또한 두 기어는 x, y, z방향으로 평면(translate) 운동을 할 수 있고 회전축 θ_x, θ_y, θ_z에 대해 회전(rotate) 운동이 가능하도록 모델링 되었다. 따라서 기어 한 개는 6자유도계를 가지므로 기어 쌍은 총 12자유도계를 갖는다. 피니언(p)의 운동방정식은 식 (1)과 같다.

Fig. 1

A three-dimensional dynamic model of a helical gear pair

$\[ m_p{\ddot{y}}_p\left(t\right)+k\cos \mathrm{\beta }\mathrm{c}\mathrm{o}\mathrm{s}\overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(1a)

$\[ m_p{\ddot{x}}_p\left(t\right)+k\cos \mathrm{\beta }\sin \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(1b)

$\[ m_p{\ddot{z}}_p\left(t\right)-k\sin \mathrm{\beta }p\left(t\right)=0 \]$

(1c)

$\[ I_p{\ddot{\mathrm{\theta }}}_{yp}\left(t\right)+k{r}_p\sin \mathrm{\beta }\cos \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(1d)

$\[ I_p{\ddot{\mathrm{\theta }}}_{xp}\left(t\right)+k{r}_p\sin \mathrm{\beta }\sin \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(1e)

$\[ J_p{\ddot{\mathrm{\theta }}}_{zp}\left(t\right)+k{r}_p\cos \mathrm{\beta }p\left(t\right)=T_p \]$

(1f)

p(t)는 기어 접촉면 법선 방향에서 기어 mesh의 상대 변위를 의미하며 식 (2)와 같이 표현할 수 있다.

$\[ p\left(t\right)=\begin{array}{l}=\left[\right(y_p-y_g)\cos \overline{\mathrm{\psi }}+(x_p-x_g\left)\sin \overline{\mathrm{\psi }}\right]\cos \mathrm{\beta }\\ +[r_p{\mathrm{\theta }}_{zp}+r_g{\mathrm{\theta }}_{zg}]\cos \mathrm{\beta }\\ +\left[\right(r_p{\mathrm{\theta }}_{yp}+r_g{\mathrm{\theta }}_{yg}\left)\cos \overline{\mathrm{\psi }}\right]\sin \mathrm{\beta }\\ +\left[\right(r_p{\mathrm{\theta }}_{xp}+r_g{\mathrm{\theta }}_{xg})\sin \overline{\mathrm{\psi }}-z_p+z_g]\sin \mathrm{\beta }-\delta \left(t\right)\end{array} \]$

(2)

식 (1)에서 T_p는 입력 토크를 의미한다. 이 연구에서는 modal summation 테크닉을 이용하여 강제 진동 응답을 계산할 때 일정한 감쇠비(damping ratio)를 적용함으로 운동 방정식에는 감쇠(damping) 요소가 표현되지 않는다. 이와 마찬가지로 기어에 대한 운동 방정식도 다음과 같이 세울 수 있다.

$\[ m_g{\ddot{y}}_g\left(t\right)-k\cos \mathrm{\beta }\cos \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(3a)

$\[ m_g{\ddot{x}}_g\left(t\right)-k\cos \mathrm{\beta }\sin \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(3b)

$\[ m_g{\ddot{z}}_g\left(t\right)+k\sin \mathrm{\beta }p\left(t\right)=0 \]$

(3c)

$\[ I_g{\ddot{\mathrm{\theta }}}_{yg}\left(t\right)+k{r}_g\sin \mathrm{\beta }\cos \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(3d)

$\[ I_g{\ddot{\mathrm{\theta }}}_{xg}\left(t\right)+k{r}_g\sin \mathrm{\beta }\sin \overline{\mathrm{\psi }}p\left(t\right)=0 \]$

(3e)

$\[ J_g{\ddot{\mathrm{\theta }}}_{zg}\left(t\right)+k{r}_g\cos \mathrm{\beta }p\left(t\right)=T_g \]$

(3f)

여기서 T_g는 입력 토크에 대한 리엑션 토크를 의미한다. 식 (1)과 식 (3)에서 m_j, I_j, J_j는 기어 j(j=p(pinion), g(gear))의 질량 및 질량 관성모멘트를 의미하며, β는 헬릭스 앵글, r_j는 기어 j의 기초원 반지름을, k는 평균 기어치 강성(averaged mesh stiffness) 값을 의미한다. 강성 값은 load distribution program (LDP)⁽¹⁶⁾로부터 계산된 값을 이용한다. 여기서 가진원으로서 δ(t)가 상대 변위 p(t)안에 포함되어야 함을 주목해야 한다. 또한 피니언과 기어에 대한 변위 벡터는 식 (4)로 정의된다.

$\[ {\mathbf{q}}_j\left(t\right)={\left[\begin{array}{cccccc}{y}_j\left(t\right)& x_j\left(t\right)& z_j\left(t\right)& {\mathrm{\theta }}_{yj}\left(t\right)& {\mathrm{\theta }}_{xj}\left(t\right)& {\mathrm{\theta }}_{zj}\left(t\right)\end{array}\right]}^T \]$

(4)

따라서 식 (1)~(3)으로부터 기어 쌍에 대한 12×12 커플링 행렬 K를 얻을 수 있다.

$\[ \mathbf{K}=\left[\begin{array}{cc}{\mathbf{K}}^{11}& {\mathbf{K}}^{12}\\ {\mathbf{K}}^{12}& {\mathbf{K}}^{22}\end{array}\right] \]$

(5)

다음으로, 기어 쌍의 강제 진동 외력 벡터는 식 (6)과 같이 정의 된다.

$\[ {\mathbf{f}}_p\left(t\right)=k\delta \left(t\right)\left\{\begin{array}{c}c\mathrm{\beta }c\overline{\mathrm{\psi }}\\ c\mathrm{\beta }s\overline{\mathrm{\psi }}\\ -s\mathrm{\beta }\\ r_{p}s\mathrm{\beta }c\overline{\mathrm{\psi }}\\ r_{p}s\mathrm{\beta }s\overline{\mathrm{\psi }}\\ r_{p}c\mathrm{\beta }\end{array}\right\},{\mathbf{f}}_{\mathit{g}}\left(t\right)=k\delta \left(t\right)\left\{\begin{array}{c}-c\mathrm{\beta }c\overline{\mathrm{\psi }}\\ -c\mathrm{\beta }s\overline{\mathrm{\psi }}\\ s\mathrm{\beta }\\ r_{g}s\mathrm{\beta }c\overline{\mathrm{\psi }}\\ r_{g}s\mathrm{\beta }s\overline{\mathrm{\psi }}\\ r_{g}c\mathrm{\beta }\end{array}\right\} \]$

(6)

식 (6)에서 s는 sin을 c는 cos을 의미한다. 따라서 기어 쌍의 운동방정식은 식 (7)과 같이 행렬 형식으로 표현할 수 있다.

$\[ \left[\begin{array}{cc}{\mathbf{M}}_p& 0\\ 0& {\mathbf{M}}_g\end{array}\right]\left\{\begin{array}{c}{\ddot{\mathbf{q}}}_p\left(t\right)\\ {\ddot{\mathbf{q}}}_g\left(t\right)\end{array}\right\}+k\left[\begin{array}{cc}{\mathbf{K}}^{11}& {\mathbf{K}}^{12}\\ {\mathbf{K}}^{12}& {\mathbf{K}}^{22}\end{array}\right]\left\{\begin{array}{c}{\mathbf{q}}_p\left(t\right)\\ {\mathbf{q}}_g\left(t\right)\end{array}\right\}=\left\{\begin{array}{c}{\mathbf{f}}_p\left(t\right)\\ {\mathbf{f}}_g\left(t\right)\end{array}\right\} \]$

(7)

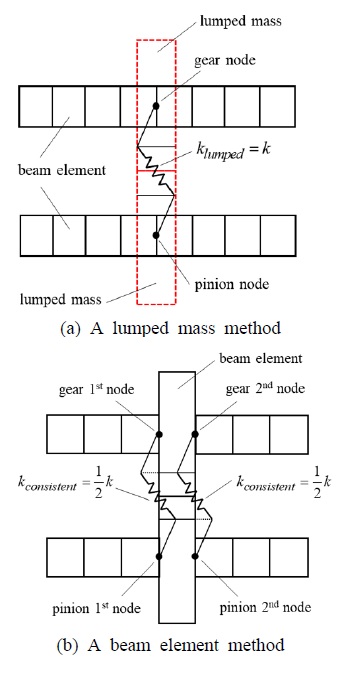
이 연구에서 공진점 예측의 정확성을 높이기 위하여 기어 바디를 변형체로 가정하였고, 샤프트 모델링 방법과 같은 오일러 빔 요소를 이용하여 모델링하였다. 반면에 기존 연구^(10~13)에서는 기어 바디를 강체로 가정하였고 기어 바디의 질량은 lumped mass 방법을 이용하여 모델링 하였다. Fig. 2에서는 기존 연구^(10~13)와 이 연구에서 사용된 헬리컬 기어 바디 모델링의 차이점을 설명하기 위해 샤프트의 형상을 단순화 시켰으며 진동 가진원인 STE는 표기를 하지 않았다. Fig. 2(a)는 이전 연구의 기어 바디 모델링 방법을 보여주고 있다^(10~13). 기어 바디를 강체로 가정하였기 때문에 기어 바디에 대한 강성 행렬은 따로 정의되지 않으며 기어의 질량 전부를 기어 노드에 집중시켰다. 따라서 식 (7)에서 질량 행렬은 기어 바디를 lumped mass로 모델링할 때의 경우를 의미한다. 또한, 위 방법에서는 피니언과 기어의 노드를 선형 스프링(평균 치 강성 값: k) 한 개를 사용하여 기어와 피니어 샤프트를 연결한다. 반면에, 이 연구에서는 Fig. 2(b)에서와 같이 기어 바디를 빔 요소로 가정함으로서 기어 바디를 12×12 강성 및 질량 행렬로 정의할 수 있다. 따라서 이 연구에서는 식 (7)의 질량 행렬은 0이 되며 기어 바디의 질량은 샤프트 모델에서 따로 정의가 된다. 또한 각 기어는 빔 요소 한 개로 정의되기 때문에 두 개의 노드가 서로 커플링이 되어야 한다. 따라서 피니언과 기어의 첫 번째 노드는 평균 치 강성의 반값(0.5k)을 갖는 선형 스프링으로 연결되고 이와 같은 방식으로 피니언과 기어의 두 번째 노드도 연결이 된다. 따라서 기어 바디를 변형체로 모델링 할 수 있으며 lumped mass를 이용한 방법보다 공진점 예측에 있어 조금 더 정확성을 높일 수 있는 특징이 있다. 위 기어 바디를 모델링하기 위해 사용된 강성 및 질량 행렬은 Meirovitch, L.⁽¹⁷⁾에서 참조하였고 각 행렬의 요소 성분은 2.2절 샤프트 모델 섹션에서 자세하게 기술되었다.

Fig. 2

The comparison of gear body models

2.2 샤프트 및 베어링 모델

샤프트 모델링을 위한 빔 요소는 식 (8a,b)에서와 같이 12×12 강성(K_i) 행렬과 질량(M_i) 행렬로 표현할 수 있다.

$\[ {\mathbf{K}}_i=\left[\begin{array}{cc}{\mathbf{K}}_i^{11}& {\mathbf{K}}_i^{12}\\ sym.& {\mathbf{K}}_i^{22}\end{array}\right],{\mathbf{M}}_i=\left[\begin{array}{cc}{\mathbf{M}}_i^{11}& {\mathbf{M}}_i^{12}\\ sym.& {\mathbf{M}}_i^{22}\end{array}\right] \]$

(8a,b)

위 식 (8a)에서 강성 행렬 K_i는 K₁, K₂, K₃의 합으로 표현할 수 있으며 각 행렬 요소 K₁, K₂, K₃는 식 (9a~c)로 정의된다.

$\[ \begin{array}{l}{\mathbf{K}}_1=\frac{E{I}_a}{l^3}\times \\ \left[\begin{array}{cccccccccccc}12& & & & & & & & & & & \\ 0& 12& & & & & & & & & & \\ 0& 0& 0& & & & & Sym.& & & & \\ 0& 6l& 0& 4l^2& & & & & & & & \\ -6l& 0& 0& 0& 4l^2& & & & & & & \\ 0& 0& 0& 0& 0& 0& & & & & & \\ -12& 0& 0& 0& 6l& 0& 12& & & & & \\ 0& -12& 0& -6l& 0& 0& 0& 12& & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& & & \\ 0& 6l& 0& 2l^2& 0& 0& 0& -6l& 0& 4l^2& & \\ -6l& 0& 0& 0& 2l^2& 0& 6l& 0& 0& 0& 4l^2& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array} \]$

(9a)

$\[ \begin{array}{l}{\mathbf{K}}_2=\frac{EA}{l}\times \\ \left[\begin{array}{cccccccccccc}0& & & & & & & & & & & \\ 0& 0& & & & & & & & & & \\ 0& 0& 1& & & & & Sym.& & & & \\ 0& 0& 0& 0& & & & & & & & \\ 0& 0& 0& 0& 0& & & & & & & \\ 0& 0& 0& 0& 0& 0& & & & & & \\ 0& 0& 0& 0& 0& 0& 0& & & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& & & & \\ 0& 0& -1& 0& 0& 0& 0& 0& 1& & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array} \]$

(9b)

$\[ \begin{array}{l}{\mathbf{K}}_3=\frac{G{J}_a}{l}\times \\ \left[\begin{array}{cccccccccccc}0& & & & & & & & & & & \\ 0& 0& & & & & & & & & & \\ 0& 0& 0& & & & & Sym.& & & & \\ 0& 0& 0& 0& & & & & & & & \\ 0& 0& 0& 0& 0& & & & & & & \\ 0& 0& 0& 0& 0& 1& & & & & & \\ 0& 0& 0& 0& 0& 0& 0& & & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \\ 0& 0& 0& 0& 0& -1& 0& 0& 0& 0& 0& 1\end{array}\right]\end{array} \]$

(9c)

여기서 l은 빔의 길이를 의미하며 E는 종탄성계수, G는 횡탄성계수, A는 빔의 단면적, I_a는 단면 2차 모멘트, 그리고 J_a는 단면 극관성 모멘트를 의미한다. 강성 행렬과 같은 방식으로 식 (8b)에서 질량 행렬 M_i는 M₁, M₂, M₃의 합으로 표현할 수 있으며 각 행렬 성분은 식 (10a~c)으로 정의된다

$\[ \begin{array}{l}{\mathbf{M}}_1=\frac{ml}{420}\times \\ \left[\begin{array}{cccccccccccc}156& & & & & & & & & & & \\ 0& 156& & & & & & & & & & \\ 0& 0& 140& & & & & Sym.& & & & \\ 0& 22l& 0& 4l^2& & & & & & & & \\ -22l& 0& 0& 0& 4l^2& & & & & & & \\ 0& 0& 0& 0& 0& 0& & & & & & \\ 54& 0& 0& 0& -13l& 0& 156& & & & & \\ 0& 54& 0& 13l& 0& 0& 0& 156& & & & \\ 0& 0& 70& 0& 0& 0& 0& 0& 140& & & \\ 0& -13l& 0& -3l^2& 0& 0& 0& -22l& 0& 4l^2& & \\ 13l& 0& 0& 0& -3l^2& 0& 22l& 0& 0& 0& 4l^2& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array} \]$

(10a)

$\[ \begin{array}{l}{\mathbf{M}}_2=\frac{I_m}{30l}\times \\ \left[\begin{array}{cccccccccccc}36& & & & & & & & & & & \\ 0& 36& & & & & & & & & & \\ 0& 0& 0& & & & & Sym.& & & & \\ 0& 3l& 0& 4l^2& & & & & & & & \\ -3l& 0& 0& 0& 4l^2& & & & & & & \\ 0& 0& 0& 0& 0& 0& & & & & & \\ -36& 0& 0& 0& 3l& 0& 36& & & & & \\ 0& -36& 0& -3l& 0& 0& 0& 36& & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& & & \\ 0& 3l& 0& -l^2& 0& 0& 0& -3l& 0& 4l^2& & \\ -3l& 0& 0& 0& -l^2& 0& 3l& 0& 0& 0& 4l^2& \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]\end{array} \]$

(10b)

$\[ \begin{array}{l}{\mathbf{M}}_3=\frac{J_{m}l}{3}\times \\ \left[\begin{array}{cccccccccccc}0& & & & & & & & & & & \\ 0& 0& & & & & & & & & & \\ 0& 0& 0& & & & & Sym.& & & & \\ 0& 0& 0& 0& & & & & & & & \\ 0& 0& 0& 0& 0& & & & & & & \\ 0& 0& 0& 0& 0& 1& & & & & & \\ 0& 0& 0& 0& 0& 0& 0& & & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& & & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& & & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& & \\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& \\ 0& 0& 0& 0& 0& 1/2& 0& 0& 0& 0& 0& 1\end{array}\right]\end{array} \]$

(10c)

또한, 식 (10a~c)에서 m은 단위 길이당 질량을 의미하며, I_m은 질량 관성 모멘트, J_m은 질량 극관성 모멘트를 의미한다.

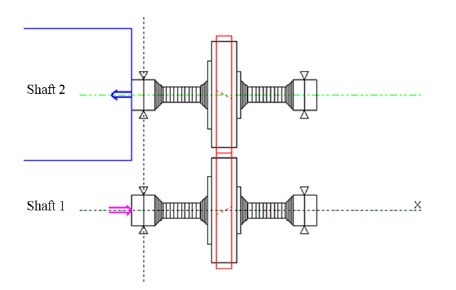
기어-샤프트-베어링의 전체 시스템은 Fig. 3에서 와 같이 모델링하였다. 샤프트 모델링은 식 (9), (10)으로 정의된 빔 요소를 이용하였고 베어링은 빔 요소 노드(node)에 스프링(6×6 강성 행렬)을 연결하는 방법을 이용하였다. 예를 들어, 샤프트가 n개의 빔 요소로 모델링 된다고 가정할 때, 식 (8a,b)의 i는 i번째 위치한 빔 요소를 의미한다. 따라서 샤프트 전체를 모델링하기 위해서는 n개의 빔 요소를 식 (11a,b)와 같이 중첩하여 연결함으로서 피니언 및 기어와 연결된 샤프트를 강성 및 질량 행렬로 모델링할 수 있다.

Fig. 3

Dynamic model of the helical geared-shaftbearing system

$\[ {\mathbf{K}}_{sj}=\left[\begin{array}{cccc}{\mathbf{K}}_{1sj}^{11}& {\mathbf{K}}_{1sj}^{12}& \mathbf{0}& \cdots \\ & {\mathbf{K}}_{1sj}^{22}+{\mathbf{K}}_{2sj}^{11}& {\mathbf{K}}_{2sj}^{12}& \cdots \\ & & {\mathbf{K}}_{2sj}^{22}+{\mathbf{K}}_{3sj}^{11}& \cdots \\ Sym& & & \ddots \end{array}\right] \]$

(11a)

$\[ {\mathbf{M}}_{sj}=\left[\begin{array}{cccc}{\mathbf{M}}_{1sj}^{11}& {\mathbf{M}}_{1sj}^{12}& \mathbf{0}& \cdots \\ & {\mathbf{M}}_{1sj}^{22}+{\mathbf{M}}_{2sj}^{11}& {\mathbf{M}}_{2sj}^{12}& \cdots \\ & & {\mathbf{M}}_{2sj}^{22}+{\mathbf{M}}_{3sj}^{11}& \cdots \\ Sym& & & \ddots \end{array}\right] \]$

(11b)

식 (11a,b)에서 아래 첨자 sj는 피니언 샤프트(sp)와 기어 샤프트(sg)를 의미한다. 마지막으로 두 개의 샤프트는 식 (12a,b)와 같이 결합되어 시스템의 전체 자유도가 여기서 결정된다.

$\[ {\mathbf{K}}_s=\left[\begin{array}{cc}{\mathbf{K}}_{sp}& \mathbf{0}\\ \mathbf{0}& {\mathbf{K}}_{sg}\end{array}\right],{\mathbf{M}}_s=\left[\begin{array}{cc}{\mathbf{M}}_{sp}& \mathbf{0}\\ \mathbf{0}& {\mathbf{M}}_{sg}\end{array}\right] \]$

(12a,b)

또한 베어링의 flexibility를 묘사하는 가장 일반적인 방법은 베어링 강성 행렬을 식 (13)과 같이 정의하고 샤프트 강성 행렬에 합 함으로써 베어링을 모델링할 수 있다.

$\[ {\mathbf{K}}_{bi}=Diag\left[\begin{array}{cccccc}{k}_{yi}& k_{xi}& k_{zi}& k_{{\mathrm{\theta }}_{yi}}& k_{{\mathrm{\theta }}_{xi}}& 0\end{array}\right] \]$

(13)

3. 해석 결과 및 모델 유효성 검증

이 연구에서는 해석 모델을 검증을 위해 기존 연구에서 수행한 실험 결과⁽¹⁴⁾와 해석 결과를 비교함로서 해석 모델의 유효성을 검증하고자 한다. Fig. 4는 가속도계를 이용하여 헬리컬 기어의 3차원 진동 값 계측에 사용한 장비이다⁽¹⁴⁾. 주요 특징으로는 일정한 토크 값이 순환되는 back-to-back 타입이며 리액션 기어박스에서 발생하는 기어 진동을 절연하기 위해 두 기어박스를 길이가 긴 샤프트, 대형 플라이 휠, 그리고 elastomer 커플링으로 연결하였다. Fig. 5는 단축과 삼축 가속도계를 샤프트 플랜지(flange)에 설치한 상태를 보여주고 있으며⁽¹⁴⁾, Fig. 6은 실험에 사용된 헬리컬 기어로 기어비 1:1, 헬릭스 앵글 25.23° , 압력각 18.22° , 치직각 모듈 2.714 mm, 물림률 2.75의 제원을 가진다⁽¹⁴⁾. 가속도계를 이용하여 3차원 진동을 계측하는 구체적인 방법은 이전 연구⁽¹⁴⁾에 자세하게 기술되어 있다.

Fig. 4

The gear dynamics test machine used to implement the measurement

Fig. 5

The test helical gear pair formed by a pinion with three tri-axial accelerometers and a gear with two un-axial accelerometers

Fig. 6

The test helical gear pair used in the previous study

이전 연구⁽¹⁴⁾에서는 기어의 3차원 진동 계측 방법을 통해 torsional(DTE), transverse(q_LA), rotational(ψ) 그리고 axial(Z) 방향의 기어 진동을 계측하였다. 우선 DTE는 torsional 방향의 진동과 아주 밀접하게 연관되었다. 이러한 이유는 가속도계의 torsional 성분을 계측하여 작용선(line-of-action)상의 전달오차를 계산하기 때문이다. 따라서 DTE는 torsional 방향의 진동으로 이해된다. 두 번째로, 기어 접촉은 작용선상에서 일어나기 때문에 기어 바디 전체가 작용선 방향으로 진동을 한다. 따라서 삼축 가속도계의 원주 방향의 성분들을 계측하여 작용선상의 진동 q_LA을 계산하였고 이는 transverse 방향의 진동으로 정의된다. 세 번째로 헬릭스 앵글로 인한 기어 바디의 rotational 진동 ψ는 Fig. 1에서 정의된 xy 평면에 놓인 임의의 축(샤프트 중심을 통과)에 대한 회전 진동으로 정의하며 그 축은 가속도 센서 위치로 결정된다⁽¹⁴⁾. ψ는 삼축 가속도계의 z방향(축방향)의 성분들을 이용하여 계산할 수 있다. 위와 유사하게 헬릭스 앵글로 인해 기어가 axial(샤프트 축 방향) 방향으로 기어가 진동을 하며 가속도계의 z방향의 성분으로 계측할 수 있으며 여기서는 Z로 표기하였다.

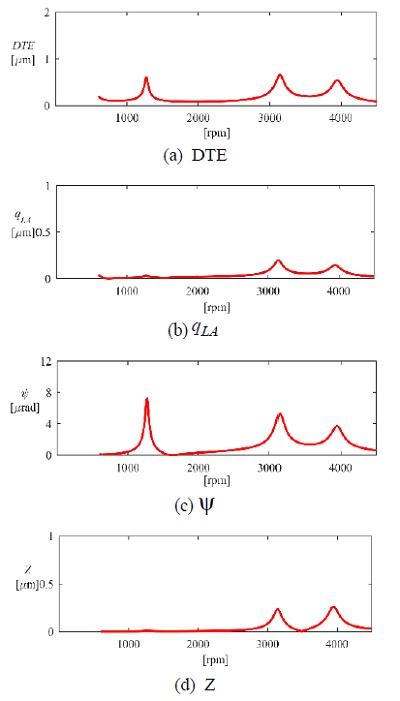
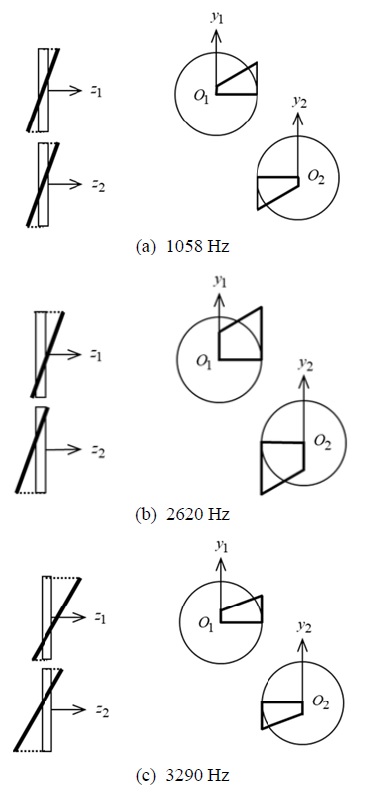
섹션 2에서 기술한 해석 방법을 이용하여 헬리컬 기어-샤프트-베어링 시스템을 모델링하였다. 해석 조건으로는 실험과 똑같은 외력 토크 100 Nm를 인가하였고 기어의 회전속도는 500 r/min부터 4500 r/min까지 50 r/min간격으로 정상상태의 강제 진동 응답을 각 RPM별로 예측하였다. 기어 모델링에서 변위 가진원 STE값은 기어 해석 프로그램(LDP)⁽¹⁶⁾에서 산출된 값을 이용하였고 1차~3차 하모닉 성분까지 반영하였다. Fig. 7(a~d)는 헬리컬 기어 시스템에서의 DTE, q_LA, ψ, Z의 해석결과를 각각 나타낸다. Fig. 7에서 보이는 바와 같이 1271 r/min, 3144 r/min, 3948 r/min에서 공진이 발생하는 것으로 계산되었고 이 공진점을 고유진동수로 환산하며 각각 1058 Hz, 2620 Hz, 3290 Hz이다. 해석 결과를 토대로 헬리컬 기어의 진동은 서로 다른 방향의 진동과 강하게 커플링이 되어 있음을 알 수가 있다. 첫 번째 공진점(1271 r/min)에서는 DTE와 ψ가 강하게 커플링이 되어 있다. 특히 이 모드에서는 ψ가 더욱 지배적임을 알 수가 있다. 더욱이 두 번째(3144 r/min)와 세 번째(3948 r/min) 공진점에서는 DTE, q_LA, ψ, Z가 모두 커플링이 되어 진동이 발생하고 있음을 알 수가 있다. 이것은 헬리컬 기어가 동적 상태에서 3차원적인 거동을 하고 있고 여러 방향의 진동들이 서로 커플링이 되어 진폭 되고 있음을 보여준다.

Fig. 7

The predicted responses of the helical gear pair

Fig. 8(a~c)에서는 각 고유진동수에서의 고유모드를 보여주고 있다. 고유모드를 이용해 위 공진점들에 대한 추가적인 분석을 하면 두 번째 고유진동수(Fig. 8(b))에는 torsional과 transverse 모드가 지배적이기 때문에 DTE 진동값이 세 공진점 중에서 제일 크다. 세 번째 고유진동수(Fig. 8(c))에서는 torsional과 transverse 모드에 비해 rotational 모드가 더 지배적이다. ψ 진동값이 두 번째 고유진동수에 진동값 보다 작지만 rotational 모드로 인해서 DTE 진폭값에 큰 영향을 준 것으로 해석할 수 있다.

Fig. 8

Predicted natural mode shapes

해석 결과를 바탕으로 헬리컬 기어의 진동은 3차원적으로 고려하는 것이 필요하며 서로 다른 방향의 진동들이 서로 강하게 커플링이 되어 있음을 예측할 수가 있다.

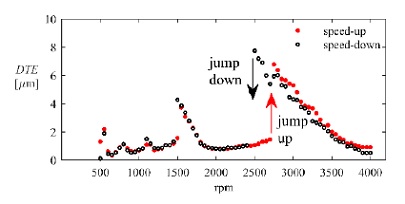
다음으로 해석결과와 실험 결과의 비교를 통해 해석 모델의 유효성을 보여주고자 한다. 두 결과를 비교 분석하기 전에 헬리컬 기어의 동적 특성이 선형적임을 설명하기 위한 목적으로 스퍼 기어의 동적 거동 특성을 우선 간략하게 설명하고자 한다. Fig. 9는 가속도계를 이용하여 스퍼 기어의 DTE를 측정한 결과이다⁽¹⁴⁾. 스퍼 기어는 일반적으로 비선형성이 강한 시스템으로 알려져 있다. 여기서 말하는 비선형이란 기어의 속도를 올려가면서 측정한 DTE와 반대로 속도를 줄이면서 측정한 DTE값이 서로 같지 않음을 의미한다. 즉, Fig. 9에서 보는 바와 같이 speed-up 조건인 경우에 주 공진점 2750 r/min에서 급작스럽게 진폭의 크기가 커지고 반대로 speed-down 조건에서는 주 공진점은 2500 r/min으로 옮겨지고 진폭이 크기 또한 급작스럽게 작아진다. 이 현상은 공진점 부근에서 기어 접촉이 순간적으로 떨어지는 tooth-separation을 의미하고 스퍼 기어의 대표적인 비선형적인 거동이다. 그러나 Fig. 10(a)에서 헬리컬 기어의 DTE 실험 결과를 보면 스퍼 기어와는 다르게 선형시스템의 일반적인 공진 곡선을 보여준다. 즉, 스퍼 기어에서 관찰되는 진폭의 jump-up과 jump-down discontinuity 현상이 발생하지 않는다. Fig. 10에서 측정된 DTE 결과와 기존 연구 사례^(10~13)의 결과를 바탕으로 헬리컬 기어를 선형 시스템으로 가정하는 것이 타당함을 보여준다. 따라서 이 연구에서 제시한 헬리컬 기어 시스템 모델에서 1) 백래쉬의 영향성 미고려, 2) time-varing 기어 치 강성을 평균 기어 치 강성(상수)으로 설정한 가정들이 합리적임을 보여준다. 백래쉬와 time-varing 기어 치 강성을 고려한다면 해석 모델의 정확성을 어느 정도 높일 수 있으나 헬리컬 기어의 전체적인 동적 거동을 예측하기 위한 필수 요건은 아니며 그러한 인자들을 무시하여도 충분히 유효한 예측 결과를 얻을 수 있다고 볼 수 있다. 기존 연구 사례⁽¹⁵⁾를 통해서도 위와 같은 내용을 확인할 수가 있다.

Fig. 9

Measured DTE amplitudes with a spur gear pair

Fig. 10

Comparisons of the measured and predicted responses of the helical gear pair

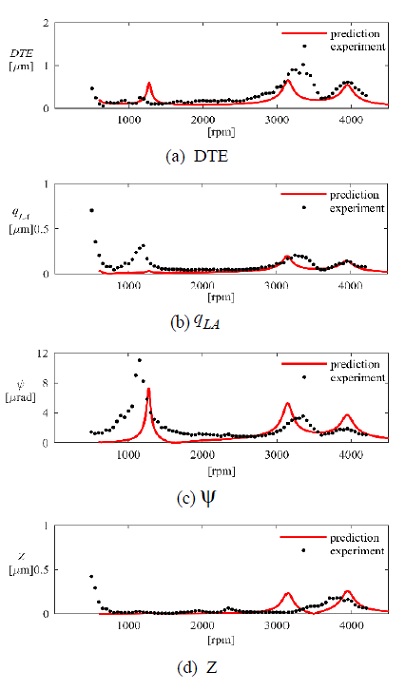
Fig. 10에서 실험결과를 보면 해석 결과와 유사하게 공진점이 1200 r/min, 3350 r/min, 3900 r/min에서 측정되었다. 여기서 해석 모델의 유효성을 정량적으로 나타내기 위해 각 공진점에 대한 진동수 차이를 Table 1에 정리하였다. 실험 결과를 참 값으로 가정하였을 때, 해석 모델은 공진점 예측에 있어 1.2 %에서 최대 6.1 %에 오차를 가지고 있음을 나타낸다. 이는 해석 모델이 고유진동수 예측에 신뢰성을 가지고 있다고 볼 수 있다.

Table 1

Comparison of natural frequencies for measured and predicted results of the helical gear system

Fig. 10(a)의 DTE 값을 비교해 보면 해석 결과가 측정 결과의 공진점과 진폭의 크기와 거의 유사함을 볼 수가 있고 전체적인 정상상태 응답 곡선이 형태도 매우 유사하다. Fig. 10(c)에서 ψ의 해석 결과도 실험 결과와 매우 흡사하게 공진 곡선을 예측하고 있음을 보여준다. Fig. 10(b)에서 첫 번째 공진점에서 측정된 q_LA와 해석 결과의 진폭의 크기가 다름을 볼 수가 있는데, 이것은 해석 모델에서 감쇠비를 상수로 가정하였기 때문에 발생하는 오차일 것으로 추정할 수가 있다. 축 방향 진동(Z)은 실험과 해석 결과 모두 전반적으로 진폭이 크기가 작음을 보여주고 있다. q_LA와 유사한 이유로 두 번째 공진점에서 진폭의 크기가 다르게 예측되었다.

실험과 해석 결과를 통해 3차원적 진동 특성은 헬리컬 기어가 내재하는 고유한 특성이며, 더 나아가 두 결과 모두 헬리컬 기어의 해석 모델링은 3차원으로 수행되어야 함을 제시한다. 따라서 이 연구에서는 기어 진동의 3차원 해석 모델을 개발하였고 실험과 해석 결과 비교 분석을 통해 해석 모델의 유효성을 보여 주었다.

4. 결 론

이 연구에서는 헬리컬 기어의 동역학 해석 모델을 제안하였고 실험결과와 비교분석을 통해 해석 모델의 유효성을 검증하였다. 기어 물림을 3차원으로 모델링을 하였고 기어 바디는 오일러 빔 요소로서 12×12 강성 및 질량 행렬로 모델링하였다. 샤프트의 flexibility를 고려하기 위해 유한요소법을 적용하여 모델링을 하였다. 마찬가지로 베어링의 flexibility는 샤프트 빔 요소 노드에 스프링으로 연결하는 방법으로 모델링하였다. 헬리컬 기어의 동역학 모델은 선형시불변(linear-time invariant) 시스템으로 가정하였는데, 이것은 이전 실험 결과⁽¹⁴⁾와 기존 연구 사례^(10~13)를 통해 그 가정의 타당함을 확인할 수 있었다. 여기서 제안한 헬리컬 기어의 진동 해석 모델은 기어의 3차원 진동을 실제와 매우 근접하게 예측 할 수 있음을 해석-실험간 결과 비교를 통해 보여주었다. 공진점 예측에 있어 실험 결과를 참값이라고 할 때 해석 모델의 결과가 최대 6.1 %이내로 예측할 수 있음을 확인했으며, 이를 통해 해석 모델이 유효함을 보여주었다. 또한, 기어치 강성값을 상수로 가정하고 STE를 변위 가진원으로 가정하는 헬리컬 기어 모델링 방법도 유효한 방법임을 보여주었다. 백래쉬 및 gyroscopic 모멘트와 같은 다소 복잡한 비선형 요소들이 해석 모델에 포함 여부가 헬리컬 기어 동적 거동의 예측 정확성 측면에서 큰 영향을 미치지 않음을 간접적으로 보여주었다.

이 연구에서 개발한 헬리컬 기어의 동역학 모델은 실제 기어시스템을 효율적으로 모델링을 가능하게함으로서 해석 시간 및 비용을 상당히 줄일 수 있는 특징이 있다. 기어 박스 설계 초기 단계에서 기어, 샤프트, 베어링 등의 다양한 설계인자를 변수로 하는 run many case 해석 모델로 확장하여 진동 측면에서 가장 바람직한 기본(fundamental) 구조 및 설계 제원을 효과적으로 찾는데 큰 역할을 할 수가 있다.

이 연구에서는 기어 동역학 해석 모델의 감쇠비를 상수로 가정하였다. 진동의 크기의 예측 정확성을 높이기 위해 이 연구에서 개발한 동역학 모델에 proportional damping 이론을 접목하여 해석 모델을 개발하고자 한다. 또한 기어 접촉에 의한 마찰력과 shuttling moment에 대한 영향성을 고려한 헬리컬 기어의 동역학 모델을 개발하고자 한다.

Acknowledgments

이 논문은 2020년도 정부(과학기술정보통신부)의 재원으로 한국연재단의 지원을 받아 수행된 기초연구사업임 (과제 번호: 2020R1G1A1014280).

References

• Kahraman, A. and Singh, R., 1990, Nonlinear Dynamics of a Spur Gear Pair, Journal of Sound and Vibration, Vol. 142, No. 1, pp. 49~75. [https://doi.org/10.1016/0022-460X(90)90582-K]
• Blankenship, G. W. and Kahraman, A., 1995, Steady State Forced Response of a Mechanical Oscillator with Combined Parametric Excitation and Clearance Type Nonlinearity, Journal of Sound and Vibration, Vol. 185, No. 5, pp. 743~765. [https://doi.org/10.1006/jsvi.1995.0416]
• Kahraman, A. and Blankenship, G. W., 1996, Interaction Between External and Parametric Excitations in Systems with Clearance, Journal of Sound and Vibration, Vol. 194, No. 3, pp. 317~336. [https://doi.org/10.1006/jsvi.1996.0361]
• Park, C. I. and Cho, D. H., 2012, Comparison of Dynamic Characteristics of Spur Gears and Helical Gears, Transactions of the Korean Society of Noise and Vibration Engineering, Vol. 22, No. 4, pp. 358~364. [https://doi.org/10.5050/KSNVE.2012.22.4.358]
• Neriya, S. V., Bhat, R. B. and Sankar, T. S., 1988, On the Dynamic Response of a Helical Geared System Subjected to a Static Transmission Error in the Form of Deterministic and Filtered White Noise Inputs, Journal of Vibration, Acoustics, Stress, and Reliability in Design, Vol. 110, No. 4, pp. 501~506. [https://doi.org/10.1115/1.3269557]
• Kahraman, A., 1993, Effect of Axial Vibrations on the Dynamics of a Helical Gear Pair, Journal of Vibration and Acoustics, Vol. 115, No. 1, pp. 33~39. [https://doi.org/10.1115/1.2930311]
• Kahraman, A., 1994, Dynamic Analysis of a Multi-mesh Helical Gear Train, Journal of Mechanical Design, Vol. 116, No. 3, pp. 706~712. [https://doi.org/10.1115/1.2919440]
• Kahraman, A., 1994, Planetary Gear Train Dynamics, Journal of Mechanical Design, Vol. 116, No. 3, pp. 713~720 [https://doi.org/10.1115/1.2919441]
• Umezawa, K., Houjoh, H. and Matsumura, S., 1996, Experimental Investigation on Modal Behavior of a Helical Gear Units with Various Ratio, ASME Power Transmission and Gearing Conference, San Diego, CA, Vol. 88, pp. 509~517.
• Kubur, M., Kahraman, A., Zini, D. and Kienzle, K., 2004, Dynamic Analysis of a Multi-shaft Helical Gear Transmission by Finite Elements: Model and Experiment, Journal of Vibrations and Acoustics, Vol. 126, No. 3, pp. 398~406. [https://doi.org/10.1115/1.1760561]
• Zhang, Y., Wang, Q., Ma, H. and Zhao, C., 2013, Dynamic Analysis of Three-dimensional Helical Geared Rotor System with Geometric Eccentricity, Journal of Mechanical Science and Technology, Vol. 27, No. 11, pp. 3231~3242. [https://doi.org/10.1007/s12206-013-0846-8]
• Zhang, H., Zhai, J., Han, Q. and Sun, W., 2015, Dynamic of a Geared Parallel-rotor System Subjected to changing Oil-bearing Stiffness due to External Load, Finite Elements in Analysis and Design, Vol. 106, pp. 32~40. [https://doi.org/10.1016/j.finel.2015.07.008]
• Yan, M. and Liu, H. Q., 2017, A Dynamic Modeling Method for Helical Gear Systems, Journal of Vibroengineering, Vol. 19, No. 1, pp. 111~124. [https://doi.org/10.21595/jve.2016.17649]
• Kang, M. R. and Kahraman, A., 2012, Measurement of Vibratory Motions of Gears Supported by Compliant Shaft, Mechanical System and Signal Processing, Vol. 29, pp. 391~403. [https://doi.org/10.1016/j.ymssp.2011.11.007]
• Sondkar, P. B., 2012, Dynamic Modeling of Double-Helical Planetary Gear Sets, Ph.D. Dissertation, The Ohio Statue University, Columbus, Ohio.
• Window-LDP, Gear Load Distribution Program, The Ohio State University.
• Meirovitch, L., 2001, Fundamental of Vibration, McGraw Hill, New York.