유동을 고려한 주기적 배열 공명기 소음저감 특성 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
The characteristics of the periodic arrangement of resonators is found to be capable of controlling reflection and transmission as a band gap phenomenon owing to the unusual sound wave caused by the periodic arrangement. In this study, the periodic arrangement of resonators was designed to analyze the noise attenuation in the frequency range of the band gap. Experiments were performed to verify the acoustic characteristics of the resonator arrangement considering the flow. CFD simulations considering the flow were performed to obtain the sound pressure level and pressure distribution, and flow analysis was performed on the designed resonator model using an unsteady compressible Navier-stokes equation. The analysis results of the periodic arrangement of the resonator were verified by comparison with the experimental results of the designed model.
Keywords:
Arrangement of Cavity, Resonator, Flow Noise, Band Gap, Compressible Flow키워드:
주기적 배열 공명, 공명기, 유동소음, 밴드 갭, 압축성 유동1. 서 론
선박, 해양플랜트 분야에서 환경 규제가 강화되면서 기존에 사용하고 있던 흡음재, 차음재 등 재료를 포함한 소음기의 사용이 제한되고 있는 실정이다. 이에 따라 기존 소음기의 성능을 유지하면서 친환경적 소음기 개발의 중요성이 대두되고 있다. 특히 환기/배기시스템의 소음허용기준을 만족하기 위해 설치되는 소음기의 대체가 필요한 실정이다. 친환경적 소음기 개발을 위해 기존 공명기 형태의 소음기를 주기적으로 배열하여 밴드 갭에 의한 음향특성을 확인하고 유동을 고려한 소음성능 검증이 필요하다.
주기적 배열에 대한 음향특성연구는 최근 여러 가지 방법으로 연구되어지고 있다. Fang 등은(1) 주기적 배열 헬름홀츠 공명기를 사용하여 밴드 갭이 형성되는 것을 확인하였다. 주기적 배열에 의한 특성으로 나타나는 소멸파(evanescent wave) 현상이 공명기 실험을 통해 검증되었으며, 헬름홀츠 공명기의 공진주파수 대역 주변에서의 주기적 배열 특성인 밴드 갭 현상이 나타나는 것을 확인했다. Wang 등은(2) 1D 헬름홀츠 공명기를 주기적으로 덕트에 적용하였을 때 음향학적 현상을 이론적으로 정리하여 공명기와 덕트의 크기에 관계없이 투과계수(T)를 도출하여 음향특성을 분석하였다. Lee 등은(3) 주기적 배열에 의한 음향특성을 확인하기 위해 1D 헬름홀츠 공명기 실험을 수행하여 위상속도(phase velocity)와 투과계수를 측정하였다. 실험결과는 덕트에 설치된 헬름홀츠 공명기의 공진주파수와 덕트의 차단(cut-off) 주파수를 비교분석하였다. Lee 등은(3) 실험결과와 비교분석을 통해 제어 주파수 이외의 주파수에서 음파가 진행되는 것을 확인하였다. King과 Cox는(4) 주기적인 배열 형태에 대해서 연구를 수행하였으며 1자유도 덕트의 음향학적 이론을 기반으로 음파 거동에 대한 행렬을 도출하였다. 또한 주기적 배열과 준주기적 배열에 대한 실험을 수행하여 투과계수를 도출하여 주기적 배열에 의한 음향학적 특성을 분석하였다. 이후 특정 주파수에서 밴드 갭이 형성하도록 멤브레인과 공명기를 결합한 모델은 위상속도를 분석하여 음향학적 특성을 검증되었다(5). Kwon 등은(6) 헬름홀츠 공명기의 주기적 배열에 대한 음향특성을 확인하기 위해 acoustic transmission line Method(ATLM)을 적용하여 헬름홀츠 공명기의 형상변화에 따른 임피던스와 전달 계수의 변화를 확인하였다(6). Farooqui 등은(7,8) 패치 형태의 공명기를 설계하여 덕트의 모든 벽면에 주기적으로 설치하여 음향학적 특성을 확인하였다. 패치 형태의 공명기에 대한 음향학적 특성을 해석적으로 검증하기 위해서 그린함수와 two-port 이론을 적용하여 해석하였으며, 해석결과는 실험결과와 비교분석하여 검증하였다.
주기적 배열 공명기를 통한 음향특성을 확인한 기존 논문은 유동을 고려하지 않은 소음제어 성능 확인이 주를 이루고 있다. 선박, 해양플랜트 등에 사용되는 소음기는 유동흐름이 존재하는 환경에 적용되기 때문에 실질적 적용을 위해 유동을 고려한 소음성능 검증이 필요한 실정이다.
Seo와 Kim은(9) 기존에 독립적으로 고려하던 음압과 유동에 대한 내용을 상호 연관된 높은 음압과 덕트를 지나는 평균 유동을 고려한 투과손실을 도출하기 위해 사각덕트 벽면에 각각 다른 임피던스를 갖는 공명기를 설치하고 실험과 기존 경험식을 기반으로 도출된 식을 검증하였다. 연구내용을 근거로 하여 효과적인 소음기 개발이 가능함을 확인하였다. Kooi와 Sarin은(10) 덕트를 지나는 유동에 의한 저항의 변화를 나타내는 유동 저항에 대한 변수를 추가하여 경험적 공식을 제안하였다. Tam 등은(11) 슬릿을 사용한 공명기 형태를 이용하여 슬릿 공명기에 대한 실험측정과 음향파의 상호작용에 대한 직접 수치해석 결과 사이의 광범위한 비교를 통해 수치적 해석결과를 검증하였다. 유동을 고려한 단일 헬름홀츠 공명기에 대한 연구는 실험과 유동소음 해석을 통해 성능 검증이 되었다. Selamet 등은(12) 덕트에 설치된 단일 공명기에 대한 유동해석을 이용하여 투과손실 값을 도출하고 실험결과와 비교분석하여 단일 헬름홀츠 공명기의 유속변화에 따른 소음성능을 검증하였다. 헬름홀츠 공명기의 공진주파수는 유속이 높아질수록 높은 주파수로 이동하며 소음제어 성능은 감소한다는 것을 확인하였다. Ghanadi 등은(13) large eddy simulation(LES) 난류모델을 도입하여 단일 헬름홀츠 공명기에 대한 유동해석을 수행하였다. 소음성능 검증은 헬름홀츠 공명기로 인해 발생되는 유동장에 대한 해석결과와 유속에 따른 공명 주변에서의 압력변동을 분석하여 확인하였다. Wu 등은(14) 공명기의 형상을 변경하여 유동을 고려한 단일 헬름홀츠 공명기의 소음성능 분석을 수행하고 기존 결과와 비교분석하여 공명기의 형태 개선에 대한 연구를 수행하였다.
이 논문에서는 주기적 배열에 대한 음향특성을 확인하기 위해 음향학적 이론을 기반으로 주기적 배열 공명기 모델을 설계하여 유동을 고려한 주기적 배열 공명기의 음향특성 및 유동에 의한 공명기의 소음성능을 해석적으로 분석하였다. 해석결과는 동일 모델에 대한 유동소음 실험결과와 비교분석하여 검증되었다. 먼저, 공명기의 이론을 이용하여 제어 주파수 대역에서 공진주파수를 갖는 공명기를 설계하였다. 설계된 공명기를 특정 간격으로 배열하여 주기적 배열의 특성이 나타나도록 주기적 배열간격을 결정하여 배치하였다. 유동을 고려한 주기적 배열 공명기의 소음성능을 분석하기 위해 비정상, 난류모델을 포함한 압축성 N-S 방정식을 이용한 수치해석 방법으로 음압레벨을 도출하였다. 해석결과와 비교분석을 위한 실험은 설계 모델과 동일하게 공명기를 덕트에 주기적으로 설치하고 압축공기로 덕트 내의 유동 환경을 만들어 유동을 고려한 유동소음 실험결과를 측정하였다. 해석결과와 실험결과를 비교하여 유동을 고려한 주기적 배열 공명기의 소음성능을 분석하였다.
2. 주기적 배열 공명기 배경이론
덕트를 진행하는 음파가 가진 주파수에 따라 공명기가 반응하게 되고, 덕트 내의 탄성률(B)의 값을 변화시킨다. 이때 덕트에 작용하는 탄성률은 유효 탄성률(Beff)이다. 덕트의 단면적을 SD로 정의하고 단위 셀(unit cell)의 단위 길이를 D라고 할 때 단위 셀당 덕트의 부피(V = SDD)가 정의된다. 덕트에서의 압력(PD)은 그 내부공기의 부피변화량(∆V)과 관련이 있다. 하지만 실제로는 공명기에서의 부피변화량(VH = SHη)이 존재하기 때문에 알짜 부피변화량(Vnet = ∆V - ∆VH)에 의해 덕트의 압력이 결정되고 식 (1)과 같이 표현된다.
| (1) |
목 부분 공기의 질량(mn)은 mn = ρSHl′으로 정의되고 변위(η)는 단순조화진동을 하고 있기 때문에 η = η0exp(iωt)의 형태를 갖는다. 이에 따라 식 (1)을 정리하면 식 (2)가 된다.
| (2) |
η값을 식 (2)에 대입하여 PD에 관해 정리하면 식 (3)과 같다.
| (3) |
유효 탄성률(Beff)은 식 (4)로 표현한다.
| (4) |
F는 VH/SDD로 filling factor라고 한다. 단위 셀 한 개에서 덕트와 공명기 간의 부피 비율이다. 식 (4)에서 보이는 것처럼 유효 탄성률 값은 공명기의 공명주파수와 filling factor에 의해 결정된다.
주기적 배열 공명기의 유효 탄성률을 구하기 위해서는 단위 셀은 덕트 벽에 설치된 단일 공명기를 포함하는 원통형 튜브로 구성된다. 주기적 배열의 경우 단위 셀의 체적변화(∆Vj)는 피스톤과 같은 형태로 작용하는 두 개의 단위 셀 경계에서 비평형 입자변위 ξj와 ξj+1가 나타남을 고려해야 하므로 ∆Vj=S(ξj+1 - ξj)의 형태로 표현한다. 따라서 단위 셀의 압력변화는 식 (5)가 된다.
| (5) |
식 (5)는 주기적 배열의 특성에 따라 식 (6)으로 표현된다.
| (6) |
단위 셀의 이론과 동일하게 정리하면 식 (7)과 같이 표현한다.
| (7) |
3. 음향해석 방법
음향에 대한 지배 방정식 (8)은 각 단일 요소 영역에 적용된다. FEM 솔루션에서 압력과 같은 모든 값은 각 요소에 대한 값으로 처리되며 형상 함수는 멤버 노드의 값을 사용하여 미분 방정식을 해결하기 위해 요소 내부의 연속 압력 값에 근사한다.
| (8) |
음향은 볼륨(V)과 그 주변 표면(S)을 고려하여야 한다. 균일한 질량 밀도를 갖는 음향 환경을 위한 식 (9)는 다음과 같다.
| (9) |
각각의 요소에 대한 질량, 강성, 하중행렬을 이용하여 식 (10)을 정리하면 다음과 같다.
| (10) |
음향 FEM에는 크게 두 가지 경제 조건이 있다. 첫 번째는 sound-hard 간의 경계 조건과 방사 경계 조건이다. 이 두 경계 조건은 각각 반사하지 않고 음파와 강체 사이의 무한히 뻗어가는 것을 해석하는데 사용된다. 입자 속도의 수직 구성요소는 강체 경계에서 사라진다.
평면파에 대한 방사 경계 조건은 식 (11)과 같다.
| (11) |
여기서 n은 경계의 수직벡터, 벡터 k는 k = kn으로 정의한다. pi는 입사파의 음파 크기이다.
4. 유동소음 수치해석 방법
덕트를 지나는 유동에 의한 음압을 정확하게 예측하기 위해서는 공명기에 의해 발생되는 유동장을 해석하는 것이 중요하다. 비정상 압축성 유동 방정식을 이용하여 유체의 흐름과 음파의 전파를 예측할 수 있다. 소스 항을 제외한 압축성 유동에 대한 방정식은 다음과 같이 표현한다(16).
| (12) |
| (13) |
| (14) |
여기서 은 열 엔탈피이다. 또한 상태 방정식은 다음과 같다.
| (15) |
변동 속도를 포함하는 항은 난류 운동으로 인한 레이놀드 스트레스에 해당하며 난류 모델을 이용하여 평균 속도장에 연결된다. 이 연구에서는 k - ε 난류 모델을 사용하며 난류 모델의 방정식 중 난류 운동 에너지 방정식은 다음과 같이 표현한다(17,18).
| (16) |
여기서 P, PNL은 다음과 같이 표현된다.
| (17) |
σk는 난류 Prandtl 수이고, ut는 난류 점성이다. 난류 감쇠 방정식은 다음과 같이 표현한다.
| (18) |
σε는 난류 Prandtl 수이고, P′, Rt, Rey는 다음과 같이 표현한다.
| (19) |
난류유동해석은 식 (12) ~ (18)를 이용한 다중 알고리즘으로 해석한다.
소음해석은 압축성 유동방정식을 이용하면 유동에 의한 덕트 내의 음파 전파가 표현되므로 특정 지점에서 음압을 도출하여 소음해석을 수행하였다. 입구에서 시간변화에 따른 유속을 식 (20)과 같이 설정한다.
| (20) |
여기서 u∈≤t은 평균 유속, a∈≤t은 진폭이며 ω은 각진동수 이다. 압력을 결정하기 위해 입구단에서 온도와 밀도는 이상기체 방정식을 이용하여 설정한다. 출구단은 음파가 반사하지 않도록 무반향 경계조건을 사용한다. 유동이 안정된 이후 공명기를 지난 덕트 내의 고정된 지점에서 시간에 따른 압력 변화를 추출하여 음파의 변화를 확인할 수 있다. 시간에 따른 유동변화에 의해 추출된 압력은 시간 영역의 결과이다. 따라서 추출된 압력은 푸리에변환을 이용하여 주파수 영역의 데이터로 변환하여 음압레벨을 도출한다.
5. 주기적 배열 공명기 유동소음 해석
5.1 주기적 배열 공명기 설계
주기적 배열 공명기를 이용한 소음기를 설계하기 위해서는 덕트에 설치하여 소음제어가 필요한 주파수대역을 확인한다. 제어 주파수대역에서 공진주파수를 갖는 공명기는 헬름홀츠 공명기 이론을 근거로 하여 목의 크기, 공명의 크기 등에 대한 주요 변수를 이용하여 설계한다. 이후 주기적 배열에 의한 특성이 나타나는 공명기 배열의 수를 결정하며 밴드 갭이 형성되는 간격을 결정한다. 배열간격은 블로흐 이론(Bloch theorem)과 브릴루앙 존(Brillouin zone)을 근거로 결정할 수 있다. 주기적 배열 공명기의 제어 주파수 대역 소음제어는 공명기의 공진주파수와 주기적 배열의 간격이 제어 주파수 대역에서 영향을 미치도록 설계되어야 소음제어 효과가 나타난다.
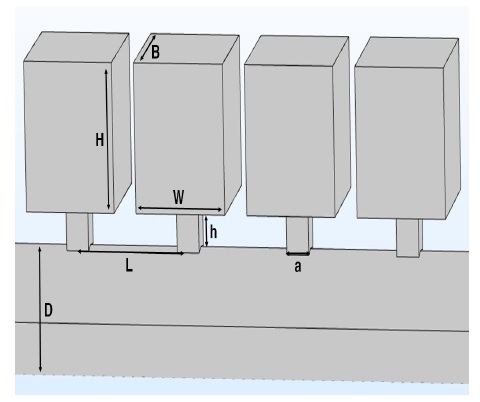
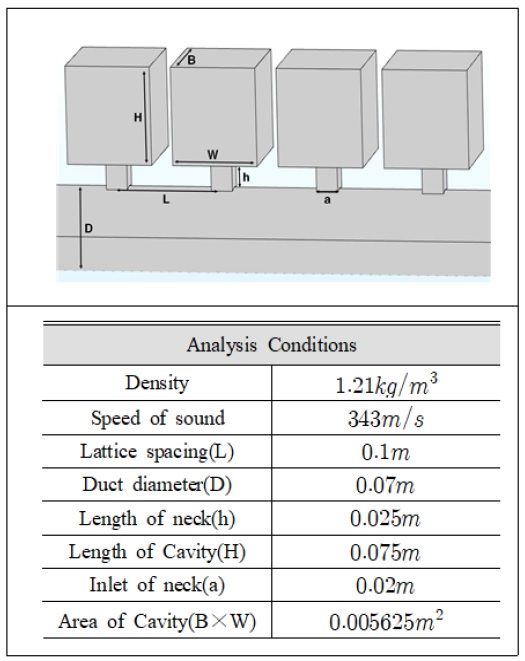
이 연구에서는 제어 주파수대역을 300 Hz이하인 저주파수 대역으로 설정하였으며, 공명기의 수는 4개로 제한한다. 공명기의 높이가 0.1 m가 되도록 설정하고 모델을 설계하였다. 공명기는 목의 길이, 면적 및 공명의 부피가 공명기의 공진주파수를 결정하는 주요 변수이다. 따라서 제어 주파수 대역에서 공진주파수를 갖는 공명기의 형태는 다양하게 변경된다. 설계 변수의 변화에 따른 최적의 모델을 찾기 위해 다양한 모델에 대한 음향해석을 진행하였다. Fig. 1은 최적의 모델로 선정된 주기적 배열 공명기이며, 단일 공명기와 주기적 배열의 주요 제원은 Table 1과 같다.
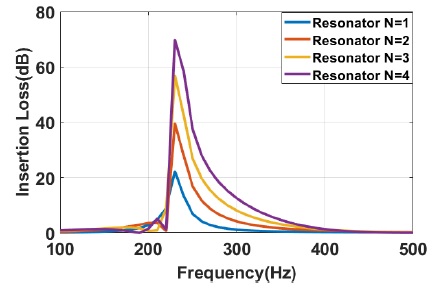
Fig. 2는 Fig. 1과 같은 제원을 갖는 주기적 배열 공명기 모델의 유동이 없는 경우에 대한 음향해석결과이다. 1개의 헬름홀츠 공명기는 공진주파수인 240 Hz에서 소음제어 효과가 나타난다. 헬름홀츠 공명기의 주기적 배열 수가 증가함에 따라 점차적으로 높은 삽입손실 값이 나타나며 갭의 크기는 증가하는 것을 확인할 수 있다. 공명기의 수가 하나일 경우는 삽입손실이 최대 22 dB의 피크 값을 나타내고 공명기의 수가 네 개일 경우는 삽입손실이 최대 69 dB이다. 공명기 네 개의 삽입손실 값이 공명기 하나의 최대 삽입손실의 크기와 동일한 크기가 나타나는 주파수는 270 Hz로 밴드갭의 크기가 넓어진 것을 확인할 수 있다.
5.2 주기적 배열 공명기 유동해석 모델
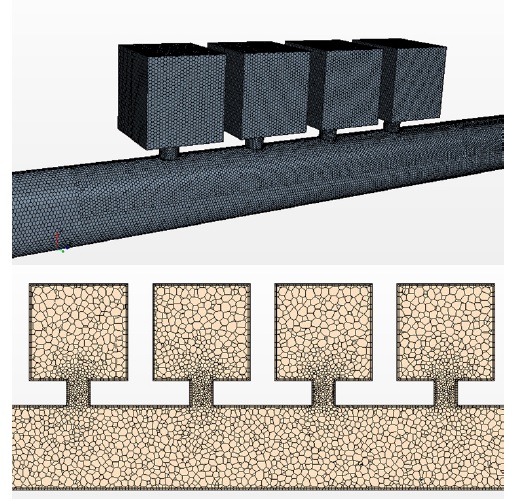
유동해석을 위한 격자 모델링은 Fig. 1과 같은 기하하적 모델을 사용하여 수행하였다. 길이 방향 길이가 4개의 공명기를 포함하여 4.4 m이다. Fig. 3은 주기적 배열 공명기에 대한 격자모델을 보여준다. 총 격자수는 약 100만개 이며, 해석 간격은 0.00001 s로 설정하였다. 덕트 내부에 전파되는 음파는 유속과 주기적 파장으로 평면파를 가정하였다. 덕트를 지나는 유동에 의한 음압 예측을 위해 3차원 압축성 RANS 방정식을 해석하였다. 압축성 이상기체 방정식은 압력 전파를 직접적으로 확인할 수 있으므로 경계조건으로 포함하여 해석을 수행하였다. 소음해석을 위한 압력 데이터의 추출 계측점은 공명기를 지나기 전 입구와 공명기를 지난 출구에서 확인하였다. Table 2는 유동해석을 위한 해석조건을 보여준다. Star CCM+ 프로그램에서 사용되는 난류모델과 해석 솔버를 사용하였으며, 덕트의 경계조건은 속도, 압력, 벽 조건을 사용하였다.
5.3 주기적 배열 공명기 실험환경
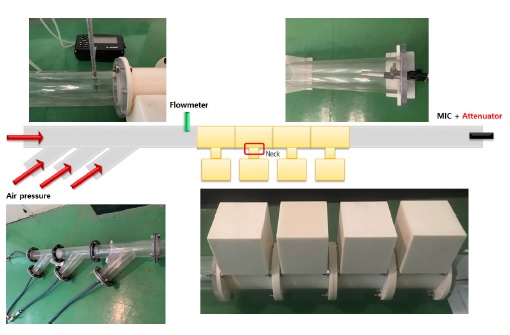
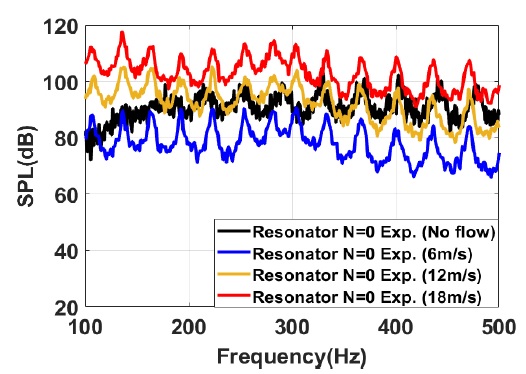
주기적 배열 공명기 유동소음 실험은 아크릴 원형 덕트와 Table 1의 주요 제원에 따라 3D 프린트로 제작된 공명기를 설치하여 수행되었다. 각각의 공명기는 연결이 가능하도록 단일 공명기로 제작하였으며 4개의 공명기를 주기적 배열하여 유동을 고려한 음향특성을 확인하기 위해 음압레벨을 측정하였다. Fig. 4와 같이 원형 덕트의 지름은 0.07 m이며 공명기 양쪽으로 각각 2 m의 덕트를 설치하였다. 유동 환경을 구현하기 위해 압축공기는 네 방향에서 유동을 보내도록 실험 장치를 구성하였다. 네 방향에서 유동이 모두 동일하게 입사하여 입사관에 의한 공명 현상이 나타나지 않도록 하였다. 덕트 내의 압축공기 유속을 측정하기 위해 공명기 앞 단에 유속 측정기를 설치하여 소음기를 지나기 전 유속을 측정하였다. 마이크는 덕트의 끝단에 설치하여 음압레벨을 측정하였다. 동일한 조건에서 실험은 3차례 수행하였다. 유동이 없는 경우 실험은 덕트 입구에서 백색소음을 소스(source)로 사용하여 동일한 방법으로 음압레벨을 측정하였다. Fig. 5는 헬름홀츠 공명기가 설치되지 않은 상태에서 각 소음원에 대한 음압레벨을 보여준다. 유동이 없는 경우 약 90 dB의 소음원이 전달되고 유동이 있는 경우 유속이 증가할수록 소음원의 크기가 증가하는 것을 확인할 수 있다.
5.4 주기적 배열 공명기 유동소음 해석과 실험 비교 검증
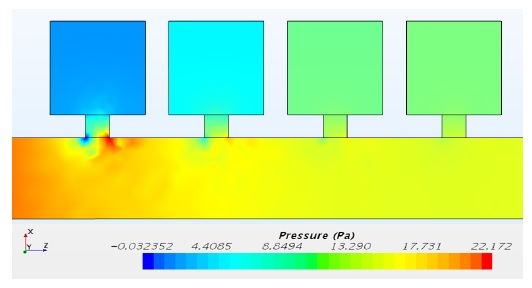
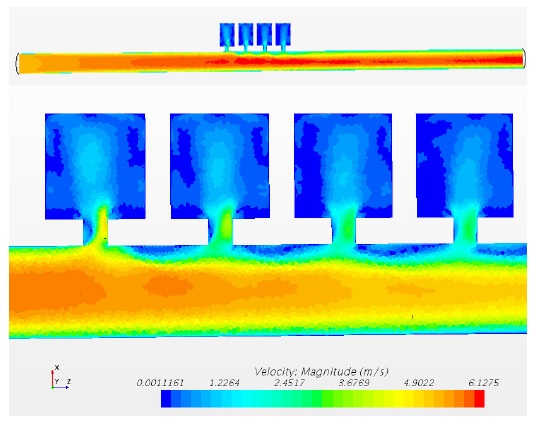
Fig. 6은 유동속도가 6 m/s인 경우 주기적 배열 공명기의 유동해석 결과로 덕트 내의 압력 분포를 보여준다. 압력분포는 공명기의 주변에서 변화가 발생하는 것을 볼 수 있다. Fig. 7은 유동속도가 6 m/s인 경우 덕트 내의 속도 분포를 보여준다. 유동 속도 변화는 덕트 전체적으로 변화가 나타나고 주기적 배열 공명기 주변을 지나가면서 급격한 변화가 나타나는 것을 확인할 수 있다.
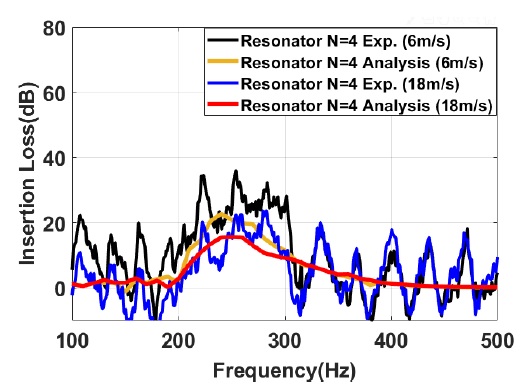
Fig. 8은 주기적 배열 공명기의 유동 유무에 따른 실험결과와 해석결과를 보여준다. 검은색 선과 파란색 선은 유속이 없는 경우와 유속이 12 m/s인 경우에 대한 실험결과이다. 노란색 선은 유동이 없는 경우에 대한 해석결과이고 빨간색 선은 공기중에서의 기준 음압 20 μPa에 대한 유동소음 해석을 통해 얻은 음압레벨 값을 이용하여 도출한 삽입손실을 보여준다. 유동이 없는 경우의 실험결과와 해석결과는 전체적인 경향이 일치하는 결과를 보여준다. 유속이 12 m/s인 경우는 뚜렷한 공진주파수는 보이지 않지만 소음저감 성능 경향은 일치하는 것을 확인할 수 있다. 주기적 배열의 특성으로 나타나는 밴드 갭의 주파수 대역은 유동유무에 관계없이 약 210 Hz ~ 300 Hz 대역에서 나타나는 것을 확인할 수 있다. 유동유무에 관계없이 밴드 갭 주파수 대역에서의 삽입손실은 해석 결과와 실험 결과가 유사하게 나타나는 것을 확인할 수 있다. 하지만 유동을 고려한 결과와 유동이 없는 경우 결과를 비교해보면 유동이 있는 경우 소음저감 효과가 뚜렷하게 저하되는 것을 확인할 수 있다. 유동유무에 따라 밴드 갭 주파수 대역에서 삽입손실 차이가 가장 큰 곳은 30 dB정도 차이를 보인다. 따라서 유동에 의한 공명기의 소음성능이 낮아지는 것을 확인할 수 있으며 밴드 갭의 주파수 대역은 변하지 않는다는 것을 확인할 수 있다.
Fig. 9는 각각 유동 유속이 6 m/s, 18 m/s인 경우 실험결과와 해석결과를 보여준다. 유동 유속이 6 m/s에서 18 m/s으로 증가함에 따라 삽입손실은 실험결과와 해석결과에서 약 5 dB ~ 10 dB 감소하는 것을 확인할 수 있다. 유동 유속 변화와 관계없이 밴드 갭의 주파수 대역은 12 m/s 실험결과와 유사한 주파수 대역을 보인다. 유속 변화에 따른 주기적 배열 공명기의 소음저감 효과는 밴드 갭 주파수 대역에서 주요하게 나타나며 밴드 갭 주파수 대역에서 실험결과와 해석결과의 음압 레벨을 비교해보면 잘 일치하는 것을 확인할 수 있다. 주기적 배열 공명기는 밴드 갭의 특성으로 유동이 없는 경우 소음저감 효과가 뚜렷하게 나타나지만 유동이 있는 경우 소음저감 효과가 현저하게 낮아지는 것을 확인 할 수 있다. 유동소음 해석을 통한 해석결과는 유속이 증가함에 따른 밴드 갭 주파수 대역과 삽입손실이 실험결과와 잘 일치하는 것을 확인할 수 있다.
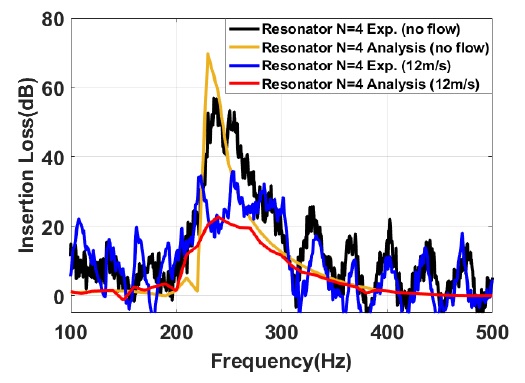
해석을 통해 주기적 배열 공명기의 유동 유무에 따른 소음성능 예측이 가능함을 확인하기 위하여 다른 공진주파수를 갖는 공명기에 대한 해석이 필요하다. Fig. 10은 주파수 400 Hz에서 공진주파수를 갖는 새로운 공명기에 대한 주요제원이다. 해석환경은 기존 수행했던 내용과 동일하게 진행한다. Fig. 11은 400 Hz 대역에서 공진주파수를 갖는 새로운 모델의 음향해석과 유동해석 결과이다. 4개의 공명기에 의한 400 Hz 주파수 대역 주변에서 밴드갭이 형성되는 것을 확인할 수 있다. 유동이 있는 경우는 공진주파수인 400 Hz에서 가장 큰 삽입손실을 보여주지만 유동에 의한 소음성능이 약 22 dB로 떨어지는 것을 확인할 수 있다. 따라서 실험과 해석으로 검증된 결과와 동일하게 공진주파수 대역 주변에서 밴드 갭이 형성되어 넓은 주파수 대역에서 소음저감 성능이 나타나고 유동에 의한 소음성능이 저하되는 것을 확인할 수 있다.
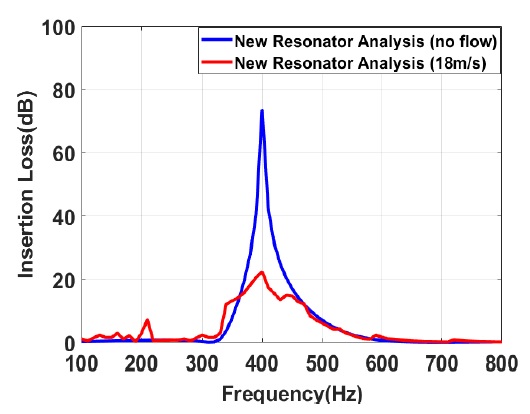
Comparison of IL obtained from experiment measurement and analysis for resonator (resonance frequency at 400 Hz) designed at no flow and 18 m/s
따라서 주기적 배열 공명기의 유동소음 해석결과는 실험결과와 비교분석하여 유동에 의한 소음저감 변화와 밴드 갭 주파수대역이 검증되었다. 또한 유동이 있는 경우에 대한 주기적 배열 공명기의 소음성능 예측이 가능함을 확인할 수 있다.
6. 결 론
이 연구에서는 유동을 고려한 주기적 배열 공명기의 음향특성 분석을 수행하기 위해 주기적 배열 공명기를 설계하고 유동소음 해석 절차에 따른 해석결과와 유동소음 실험을 통해 얻은 계측결과와 비교 분석을 수행하였다.
주기적 배열 공명기 모델은 주기적 배열에 의한 음향특성으로 나타나는 밴드 갭이 형성되는 주기적 간격을 설정하여 실험모델을 설계하였으며 밴드 갭 주파수 대역이 저주파수 대역에서 형성되도록 설계하였다. 유동소음 해석은 유동에 의한 음압을 정확하게 예측하기 위해서 비정상 압축성 RANS 방정식을 이용하여 유체의 흐름과 음파의 전파를 해석하였다. 유동을 고려한 유동소음 실험은 유동환경을 구현하기 위해 덕트 내의 압축공기를 분사하여 덕트 끝단에서의 음압레벨을 측정하였다. 실험결과와 해석결과는 주기적 배열의 특성으로 나타나는 밴드 갭의 주파수 대역이 잘 일치하는 것을 확인할 수 있었다. 또한 유동 유무에 따른 소음성능을 확인하기 위해 유속이 없는 경우와 비교하여 유동에 의한 소음성능 감소에 대한 결과를 확인하였다. 유속변화에 따른 소음성능을 확인하기 위해 유속이 6 m/s, 12 m/s, 18 m/s인 경우에 대한 실험결과와 해석결과를 비교하여 소음성능을 검증하였다. 이를 통해 유동을 고려한 주기적 배열 공명기에 대한 유동소음 성능 예측과 밴드 갭의 형성 주파수 대역을 해석적으로 확인할 수 있다.
이 연구로부터 유동을 고려한 주기적 배열 소음기의 소음성능을 분석하여 유동흐름이 존재하는 환경에 적용 가능한 주기적 배열 소음기 개발이 가능할 것으로 기대된다.
Acknowledgments
이 연구는 서울대학교 BK21 해양플랜트 창의인재 양성사업단 및 연구재단(2019R-1F1A1062914)의 지원을 받아 수행하였습니다. 또한, 해양시스템공학연구소(RIMSE)의 지원을 받아 수행하였습니다.
References
-
Fang, N., Xi, D., Xu, J., Ambati, M., Srituravanich, W., Sun, C. and Zhang, X., 2006, Ultrasonic Metamaterials with Negative Modulus, Nature Materials, Vol. 5, No. 6, pp. 452~456.
[https://doi.org/10.1038/nmat1644]

-
Wang, Z. G., Lee, S. H., Kim, C. K., Park, C. M., Nahm, K. and Nikitov, S. A., 2007, Effective Medium Theory of The One Dimensional Resonance Phononic Crystal, Journal of Physics: Condensed Matter, Vol. 20, No. 5, Article no. 055209.
[https://doi.org/10.1088/0953-8984/20/5/055209]

-
Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G. and Kim, C. K., 2009, Acoustic Metamaterial with Negative Modulus, Journal of Physics: Condensed Matter, Vol. 21, No. 17, Article no. 175704.
[https://doi.org/10.1088/0953-8984/21/17/175704]

-
King, P. D. C. and Cox, T. J., 2007, Acoustic Band Gap in Periodically and Quasiperiodically Modulated Waveguides, Journal of Applied Physics, Vol. 102, No. 1, Article no. 014902.
[https://doi.org/10.1063/1.2749483]

-
Lee, S. H., Park, C. M., Seo, Y. M., Wang, Z. G. and Kim, C. K., 2010, Composite Acoustic Medium with Simultaneously Negative Density and Modulus, Physical Review Letters, Vol. 104, No. 5, Article no. 054301.
[https://doi.org/10.1103/PhysRevLett.104.054301]

-
Kwon, B. J., Jo, C., Park, K. C. and Oh, I. K., 2009, Wave Propagation Characteristics of Acoustic Metamaterials with Helmholtz Resonators, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 23, No. 2, pp. 167~175.
[https://doi.org/10.5050/KSNVE.2013.23.2.167]

-
Farooqui, M., Elnady, T. and Akl, W., 2016, Validation of Low Frequency Noise Attenuation Using Locally Resonant Patches, The Journal of the Acoustical Society of America, Vol. 139, No. 6, pp. 3267~3276.
[https://doi.org/10.1121/1.4950736]

-
Farooqui, M., Elnady, T. and Akl, W., 2016, Sound Attenuation in Ducts Using Locally Resonant Periodic Aluminum Patches, The Journal of the Acoustical Society of America, Vol. 139, No. 6, pp. 3277~3287.
[https://doi.org/10.1121/1.4948990]

-
Seo, S.-H. and Kim, Y.-H., 2005, Silencer Design by Using Array Resonators for Low-Frequency Band Noise Reduction, The Journal of the Acoustical Society of America, Vol. 118, No. 4, pp. 2332~2338.
[https://doi.org/10.1121/1.2036222]

-
Kooi, J. and Sarin, S., 1981 An Experimental Study of the Acoustic Impedance of Helmholtz Resonator Arrays Under a Turbulent Boundary Layer, In 7th Aeroacoustics Conference, California, United States, pp. 1981~1998.
[https://doi.org/10.2514/6.1981-1998]

-
Tam, C. K., Ju, H., Jones, M. G., Watson, W. R. and Parrott, T. L., 2005, A Computational and Experimental Study of Slit Resonators, Journal of Sound and Vibration, Vol. 284, No. 3-5, pp. 947~984.
[https://doi.org/10.1016/j.jsv.2004.07.013]

-
Selamet, E., Selamet, A., Iqbal, A. and Kim, H., 2011, Effect of Flow on Helmholtz Resonator Acoustics: A Three-dimensional Computational Study vs. Experiments, SAE Technical Paper, Article no. 2011-01-1521.
[https://doi.org/10.4271/2011-01-1521]

-
Ghanadi, F., Arjomandi, M., Cazzolato, B. and Zander, A., 2014, Understanding of The Flow Behaviour on a Helmholtz Resonator Excited by Grazing Flow, International Journal of Computational Fluid Dynamics, Vol. 28, No. 5, pp. 219~231.
[https://doi.org/10.1080/10618562.2014.922681]

-
Wu, G., Lu, Z., Xu, X., Pan, W., Wu, W., Li, J. and Ci, J., 2019, Numerical Investigation of Aeroacoustics Damping Performance of a Helmholtz Resonator: Effects of Geometry, Grazing and Bias Flow, Aerospace Science and Technology, Vol. 86, pp. 191~203.
[https://doi.org/10.1016/j.ast.2019.01.007]

- Kinsler, L. E., 2000, Fundamentals of Acoustics (4th ed.), New York, Wiley, Chap 10, pp. 284~286.
- Methodology, STAR-CD(Version 4.12), 2009, Computer Software, CD-adapco, Melville, NY.
-
Tahry, S. H. E., 1983, K-Epsilon Equation for Compressible Reciprocating Engine Flows, Journal of Energy, Vol. 7, No. 4, pp. 345~353.
[https://doi.org/10.2514/3.48086]

-
Lien, F. S., 1996, Low-Reynolds-number-eddy-viscosity Modeling Based on Nonlinear Stress-Strain/Vorticity Relations, Proceedings of the 3rd Symposium on Engineering Turbulence Modeling and Measurements.
[https://doi.org/10.1016/B978-0-444-82463-9.50015-0]


Jae-Yong Kim received the B.S degree in Naval Architecture and Ocean Systems Engineering from Kyungnam University in 2014. He is currently working toward the Ph. D. degree in noise and vibration at Seoul National University. He is especially interested in predicting acoustic performance of the silencers and acoustic metamaterials.

Jee-Hun Song received his B.S. degree in Naval Architecture and Ocean Engineering from the Seoul National University, Korea, in 2003, and his Ph.D. in 2007. Currently he is a professor of Naval Architecture and Ocean Engineering at Chonnam National University, Korea. His primary research interest is vibration and noise analysis in structures.