주변 유체와 연성된 수중 구조물의 진동분석을 위한 스펙트럼 요소법

1. 서 론

원자력 발전에서 사용되는 중수로는 급수펌프를 이용하여 핵연료봉 집합체에 중수를 가압하여 핵분열을 일으키는 원리를 사용한다. 이 때 가압된 중수에 의해 발생되는 압력파는 핵연료봉 집합체를 가진하여 구조적인 불안전성을 발생시킨다. 구조적인 불안전성을 억제하기 위해서는 핵연료봉 집합체의 진동특성을 분석하고, 불안전한 거동을 제어할 수 있는 지지격자의 설계가 필요하다⁽¹⁾.

핵연료봉 집합체의 진동 특성을 분석하기 위해서는 유한요소법을 가장 보편적으로 사용한다. 유한요소법으로 형상함수를 사용하여 핵연료봉 집합체의 구조와 유체를 각각 모델링하고 접촉면에 대해 표면속도와 압력구배를 연성시켜 행렬 방정식을 유도할 수 있다^(2,3). 하지만, 구조와 유체가 연성된 수중 구조물의 거동을 유한요소법으로 계산하게 되면 해석의 정확성을 검증하기 위해 수많은 시행착오를 해야 한다. 또한, 고주파수의 진동해석에 대해서는 사용되는 요소의 개수가 증가하고 계산되는 행렬의 크기가 증가하여 계산시간이 많이 소모된다.

유한요소법의 정확성과 시간 경제성을 극복하는 방법으로 스펙트럴 요소법이 개발되었다. 스펙트럴 요소법은 편미분방정식의 해의 기저에 대한 형상함수를 사용하기 때문에 요소와 노드점의 개수가 적어도 정확한 해를 구할 수 있다. 스펙트럴 요소법은 주로 구조해석에서 사용되지만 형상이 단순한 구조물에 대해 구조 유체 연성해석에서도 응용되고 있다. 가장 먼저 배관계의 내부 정상 유동에 따른 구조진동의 특성을 연구한 사례가 있다⁽⁴⁾. 또한, 배관계의 비정상 유동과 파이프의 변위가 상호작용된 진동해석도 연구되었다⁽⁵⁾. 더 나아가 압력에 따라 단면적이 변하는 유연관에 대해서도 스펙트럴 요소법이 적용된 연구가 존재한다⁽⁶⁾. 스펙트럴 요소법을 이용하여 외부유동을 모사하거나 구조물 간의 질량연성을 고려한 진동해석은 수행되었으나 수치해석 결과에 대한 정확성이 검증되지 않았다⁽⁷⁾.

이 연구에서는 가장 먼저 핵연료봉 집합체의 구조진동에 대한 방정식을 도출하였다. 수중 구조물의 부가질량과 주변 압력을 계산하여 스펙트럴 요소법에 적용하였다. 스펙트럴 요소법의 정확성과 시간 경제성을 검증하기 위해 유체 구조 연성을 고려한 유한요소 방정식을 사용하여 결과 비교 및 고찰을 수행하였다.

2. 수중 구조물의 진동 해석을 위한 스펙트럴 모델링

2.1 수중 구조물의 지배방정식

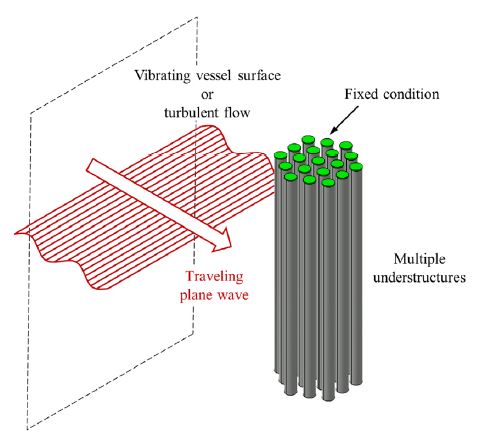
Fig. 1과 같이 중수로에서 사용하고 있는 핵연료봉 다발체는 다수의 원형 실린더 구조물로 이루어져 있다. 급수펌프의 작동으로 인해 핵연료봉 보관용기의 표면진동과 난류유동이 발생하여 유체의 압력변동을 일으켜 평면파의 형태로 수중 구조물에 도달하게 된다. 평면파가 다발체 부근에 도달하게 되면 입사파와 함께 구조물 간 벽면에 의해 산란파가 발생되어 진동을 일으킨다^(8,9).

Fig. 1

Flexural vibration of underwater structures subjected to traveling plane wave

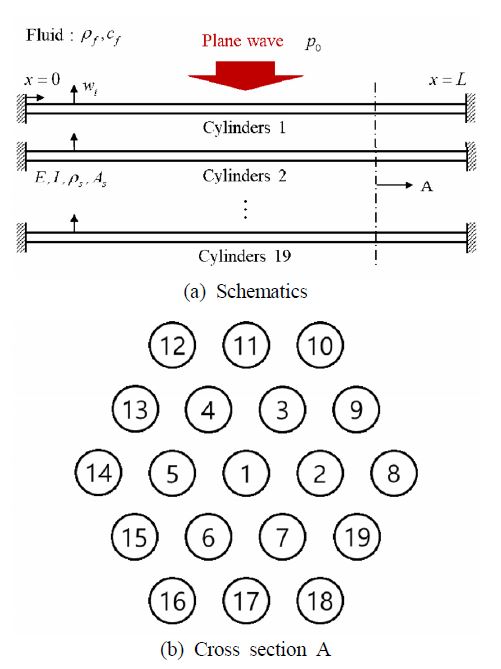
Fig. 2와 같이 핵연료봉 집합체의 굽힘 진동을 계산하기 위해 개별 연료봉을 원형보로 모델링하였다. 또한, 핵연료봉 집합체의 배치는 중수로에서 사용하는 CANDU형 가압 중수로에서 사용하는 핵연료봉 집합체로 가정하였다⁽¹⁰⁾. 이를 통해 i번째의 보에 대한 파동방정식을 다음과 같이 나타냈다.

Fig. 2

Underwater structures consisting of 19 cylinders

$\[ EI\frac{{\partial }^4{w}_i}{\partial x^4}+{\rho }_s{A}_s\frac{{\partial }^2{w}_i}{\partial t^2}=F_{\upsilon ,i}+F_{p,i} \]$

(1)

여기서 E는 보의 탄성계수, I는 관성모멘트, ρ_s는 보의 밀도, A_s는 보의 단면적, i는 보의 번호로서 1에서 N까지의 범위를 갖는다. x와 t는 각각 보의 진동에 대한 위치와 시간 변수이며, w_i는 보의 변위를 나타낸다. F_v는 점성 유체력을 말하며, F_p는 유체에 의해 전달되는 외력을 말한다. 점성 유체력은 유체의 밀도와 감쇠에 의해 결정되며, 유체가 공기인 경우에는 무시할 수 있다. 압력파에 의한 힘은 외부의 충격이나 난류에 의해 발생된다.

점성 유체력 F_v는 정제된 유체의 헬름홀츠 방정식을 사용하며 다음과 같이 계산하였다.

$\[ F_{\upsilon ,i}=-{\rho }_f\pi R_i^2\sum _{i=1}^N{\alpha }_{il}{\ddot{w}}_l \]$

(2)

여기서 ρ_f는 유체의 밀도, R은 원형보의 반지름을 말한다. α_il는 l번째 보의 진동에 의한 i번째 보의 무차원 부가질량을 뜻하며, 집합체의 연료봉 벽면 경계조건과 식 (2)에 의해 결정된다. 단일 연료봉의 경우에는 무차원 부가질량이 1로 계산되며, 다수의 경우는 주변 연료봉과의 간격으로 인해 스퀴즈 필름 효과가 발생하여 부가질량이 1보다 크게 나타난다. 또한, 유체의 점성에 의한 감쇠력이 증가할수록 무차원 부가질량의 허수부가 증가하며 구조물의 진동에 대한 감쇠효과가 향상된다.

외력 F_p을 계산하기 위해서는 핵연료봉 집합체의 주변 압력을 사용해야 한다. 집합체의 주변 압력은 다음과 같이 음향 파동방정식의 다중 산란파 이론을 사용하였다⁽¹¹⁾.

$\[ \begin{array}{l}p\left(r_i,{\theta }_i\right)=\sum _{n=-\infty }^{\infty }\left[\begin{array}{c}\\ p_0{e}^{-\mathrm{i}{k}_f\gamma }{\mathrm{i}}^n{J}_n\left(k_f{r}_i\right)e^{\mathrm{i}n{\theta }_i}+\\ \end{array}\right.\\ \left.\sum _{\begin{array}{c}j=1\\ j\ne i\end{array}}^N{B}_{n,j}\sum _{n=-\infty }^{\infty }{H}_{n-m}^{\left(1\right)}\left(k_f{R}_{ij}\right)e^{\mathrm{i}\left(n-m\right){\psi }_{ij}}{J}_m\left(k_f{r}_i\right)e^{\mathrm{i}m{\theta }_i}\right]\end{array} \]$

(3)

여기서 p₀는 입력파의 압력크기, γ는 입력파의 시작점 좌표, J_n은 n차 1종 베젤함수, B_n는 경계조건에 의해 결정되는 계수를 뜻한다. 경계조건은 원형보의 벽면조건을 사용하였으며, 식은 다음과 같다.

$\[ {\left.\frac{\partial p}{\partial r_i}\right|}_{r_i=R_i}=0, i=\mathrm{1,2},\cdots ,N \]$

(4)

입력파에 의해 발생되는 외력은 주변 산란파에 의한 압력을 적분하여 다음과 같이 계산하였다.

$\[ F_{p,i}={\int }_0^{2\pi }p\left(R_i,{\theta }_i\right)R_i\cos {\theta }_{i}d{\theta }_i \]$

(5)

3. 검증을 위한 유체-구조 연성해석의 유한요소 모델링

스펙트럴 요소법의 정확성을 검증하기 위해 유체-구조 연성을 고려한 유한요소법을 사용하여 핵연료봉 집합체의 수치해석 모델을 구축하였다. 핵연료봉 집합체는 3차원 고체의 파동방정식을 사용하였으며, 식은 다음과 같다⁽¹²⁾.

여기서 ü는 구조물의 3차원 가속도벡터를 뜻하며, σ는 구조물의 응력 텐서, F는 외력 벡터. R은 유체로부터 받는 반력을 뜻한다. 핵연료봉 주변의 유체는 점성유체의 3차원 음향 파동방정식을 사용했으며, 식은 다음과 같다.

여기서 p는 유체의 압력섭동을 말하며, v는 유체의 동점성계수, c는 유체의 음속, r_f는 고체표면으로부터의 반력을 뜻한다. 유한요소법을 통해 식 (12)와 (13)을 행렬로 표현하면 다음과 같이 유체 구조 연성을 고려한 방정식을 유도할 수 있다⁽¹³⁾.

여기서 u_s는 고체의 변위행렬, p은 유체의 압력행렬, M_s, K_s는 고체의 질량, 강성행렬, M_f, C_f, K_f는 유체의 질량, 감쇠, 강성행렬, f_s, f_f는 각각 고체와 유체의 외력행렬을 뜻한다. S는 표면행렬로 고체와 유체가 만나는 면의 형상함수를 서로 곱한 후 적분하여 계산하였다.

스펙트럴 요소법과 비교하기 위해 식 (14)의 해를 조화함수의 형태로 가정하여 다음과 같이 주파수에 대한 변위응답과 압력으로 나타내었다.

여기서 u_s, p, f_s, f_f는 주파수에 대한 함수로 앞서 스펙트럴 요소법으로 유도된 변위행렬과 비교가 가능하였다.

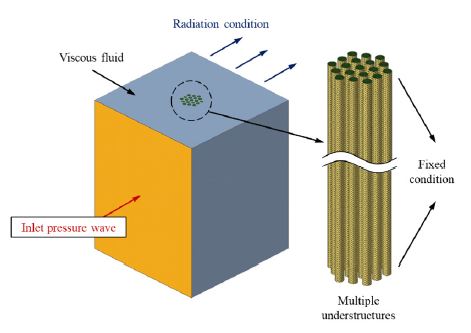
Fig. 3과 같이 유한요소법의 경계조건으로는 앞서 스펙트럴 요소법과 동일하게 핵연료봉 다발체의 양 끝단에 고정단 조건을 주었다. 다발체 주변의 유체에 대해서는 평면파의 패턴이 같을 수 있도록 입력조건과 무반사조건을 주어 스펙트럴 요소법에서 사용하는 압력장과의 패턴을 비교하였다.

Fig. 3

Boundary condition of finite element method for underwater structures

4. 스펙트럴 요소법과 유한요소법의 해석결과를 통한 비교분석

핵연료봉을 반지름이 0.005 m, 길이가 0.5 m인 원형보 가정하였고, 재질은 지르코늄(E = 68 GPa, ρ_s = 6,520 kg/m³)으로 설정하였다. 집합체 주변의 액체는 온도 40℃인 중수(ρ_f = 1100 kg/m³, c = 1400 m/s, v = 0.713×10^-6 m²/s)로 가정하였다. 핵연료봉의 개수는 1개, 7개, 19개로 늘려가면서 진동 특성을 비교하였다.

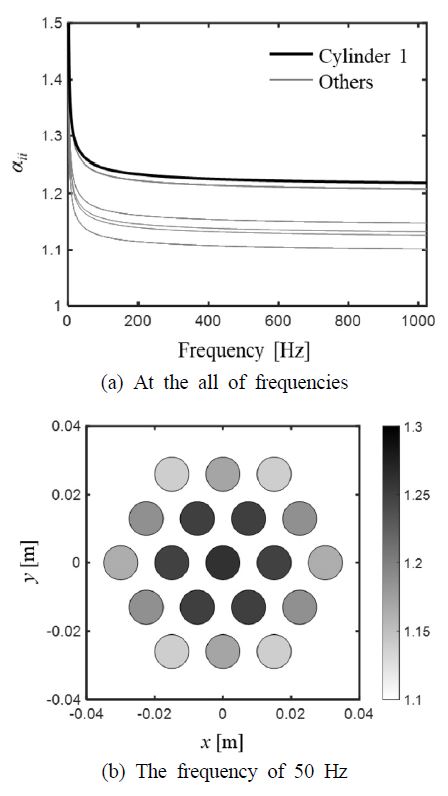
Fig. 4는 다발체의 각 원형보에 대해 무차원 부가질량을 계산한 결과이다. 무차원 부가질량은 가진주파수가 증가할수록 수렴하는 경향을 보였으며, 다발체의 가장 중앙인 1번째 실린더에서 높은 부가질량 값이 계산되었다. 또한, 가장자리로 갈수록 부가질량이 상대적으로 낮음을 관찰하였다. 이는 주변 구조물들의 거리가 가까워져 스퀴즈 필름 효과가 발생하여 부가질량이 증가한 것으로 보인다.

Fig. 4

Predicted added masses of underwater structures

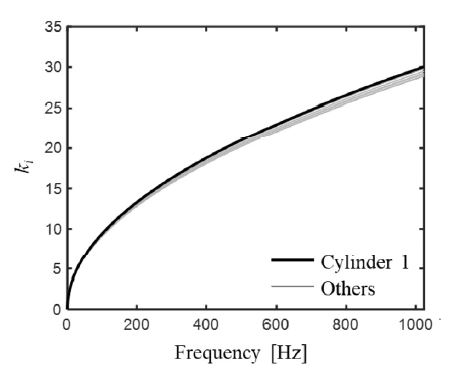
Fig. 5는 다발체의 각 원형보에 대해 분산곡선을 계산한 결과이다. 모든 보에 대해서 분산곡선의 거의 유사하게 나타나지만, 1번째 실린더에서 주파수에 따른 파수의 증가량이 가장 높은 것으로 관찰되었다. 보의 음속은 영률과 질량, 단면적의 제원에 따라 달라지는데, 부가질량이 상대적으로 높은 1번째 실린더가 다른 보에 비해 음속이 낮아져 파수가 높은 것으로 판단된다. 또한, 다발체의 개별 보마다 크기가 다른 파수가 계산되었으며, 이를 통해 실린더 간의 모드가 예측될 것으로 보였다.

Fig. 5

Predicted dispersion curve of underwater structures

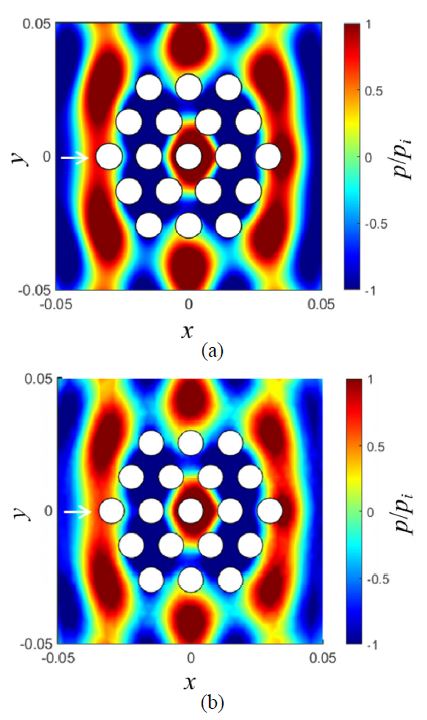
Figs. 6과 7은 다발체 구조물의 압력파가 도달했을 때의 압력장 무늬를 관찰한 결과이다. 식 (3)으로 계산된 해와 유한요소법에서 계산된 압력장 패턴이 매우 유사하였다. 이를 통해 이 연구에서 사용된 유한요소 모델의 결과값이 비교적 정확하다는 것을 알 수 있었다. 또한, 입력파의 가진주파수가 증가할 수록 압력장의 패턴이 복잡하게 나타나는 경향을 보였다. 이는 저주파수의 가진은 모든 원형보에 대해서 힘의 크기와 방향이 일정하지만, 고주파수로 갈수록 원형보에 따라 힘이 다르게 작용될 것으로 분석되었다.

Fig. 6

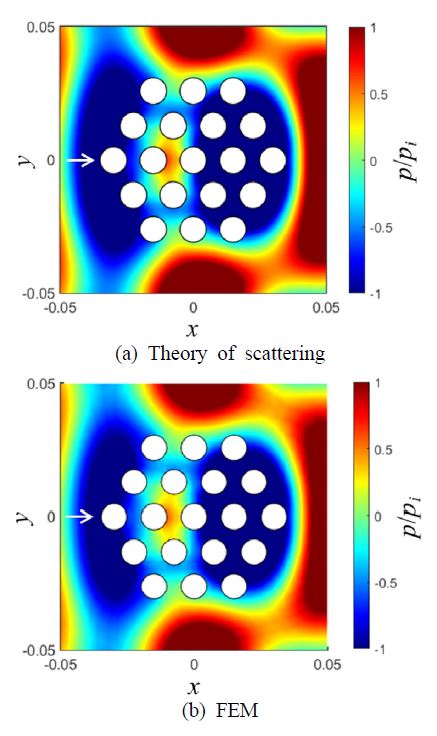
Comparison with predicted pressure wave patterns near 19 cylinders induced by the plane wave with a wavelength of kfR = 0.5 by using (a) and (b)

Fig. 7

Same as Fig. 6, but kfR = 1.0

Fig. 8과 같이 입력파에 대하여 다발체 내부의 개별보에 작용하는 외력의 크기를 비교하였다. 외력은 입력파의 주파수와 비례하는 경향을 보였다. 또한, 중심으로부터 가장 외곽에 위치하는 10, 12, 16, 18번째의 구조물에 작용하는 외력이 다른 구조물에 비해 외력의 크기가 상대적으로 높았다. 또한, 안쪽에 위치한 구조물의 외력은 상대적으로 바깥쪽에 비해 낮게 작용했다.

Fig. 8

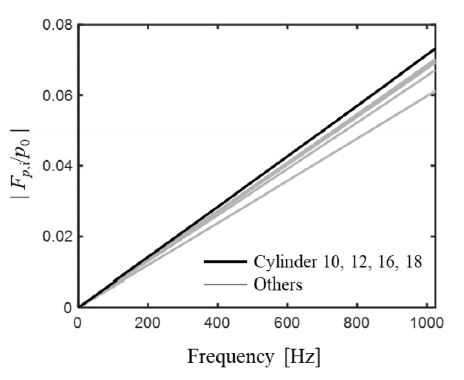
Amplitudes of pressure forces acting on the underwater structures induced by traveling plane wave and scattering wave

Fig. 9는 다발체의 실린더 개수를 변경해가면서 입력파의 크기에 대한 변위 전달함수를 비교한 결과이다. 단일 원형 보의 경우는 일반 보의 전달함수와 유사하게 예측되는 반면에 실린더의 개수가 많아질수록 2번째 모드에서 공진주파수가 분리되는 것을 알 수 있었다. 이는 실린더 간의 위상차에 의해 발생되는 모드로 인한 것으로 알려져 있다⁽⁷⁾. 다른 모드에 대해서는 입력파의 파장이 구조물의 간극에 비해 넓기 때문에 위상차가 존재하지 않고 진동하여 중첩모드가 발생하지 않은 것으로 예측된다.

Fig. 9

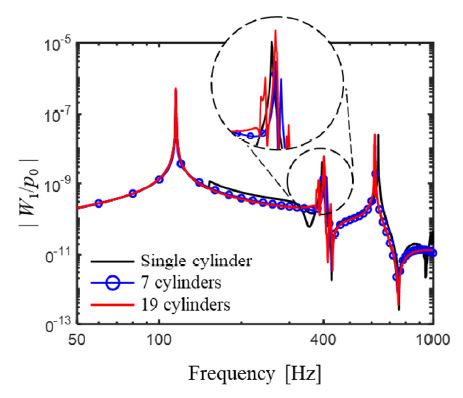
Transfer function for underwater structures varying the number of cylinders subjected to pressure force

Table 1의 유한요소법에서 사용된 요소의 개수를 살펴보면 스펙트럴 요소법에 비해 매우 많은 것을 알 수 있다. 유한요소법의 경우, 요소의 개수가 증가하게 되면, 해석의 정확도가 향상되지만 계산량이 많아져 해석속도가 늦어진다. 반면에 스펙트럴 요소법을 사용하게 되면, 요소의 개수가 유한요소법에 비해 상대적으로 적어 해석속도가 빠르다.

Table 1

Comparison with the numbers of used elements for underwater structure consisting of 19 cylinders

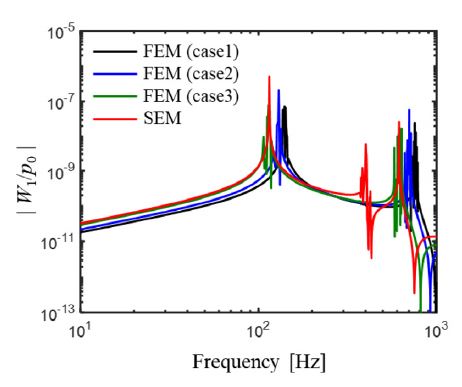
Fig. 10은 스펙트럴 요소법과 유한요소법의 전달함수를 비교한 결과이다. 요소의 개수가 많은 case3의 경우는 case1과 2에 비해 스펙트럴 요소법과의 공진주파수가 거의 일치하는 경향을 보였다. 또한, 스펙트럴 요소법은 유한요소법에 비해 요소의 개수가 작음에도 불구하고 유한요소법의 전달함수와 매우 유사하게 계산되었다. 게다가 유한요소법에서 예측하지 못했던 2차 모드를 스펙트럴 요소모델에서 예측되어 해석의 정확성과 해석시간의 경제성을 모두 검증할 수 있었다.

Fig. 10

Comparison with predicted transfer function using SEM and FEM

5. 결 론

이 논문에서는 주변 유체와 연성된 구조물의 진동 특성을 분석하기 위해 스펙트럴요소 모델을 유도하고 기존의 유한요소 모델과 비교하여 정확성을 검증하였다. 대상 구조물은 중수로에서 사용하는 핵연료봉 다발체를 선택하였고, 연료봉을 원형보로 가정하여 파동방정식을 유도하였다. 급수펌프에서 발생하는 입사파를 모델링하기 위해 산란파의 해를 사용하였다. 유도된 파동방정식은 해의 기저를 통한 형상함수를 이용하여 스펙트럴요소 방정식을 유도하였다. 해석의 정확성을 확인하기 위해 3차원 유한요소 모델을 사용하여 유체와 구조물을 모델링하였다.

다발체 내부의 실린더 별로 부가질량을 계산한 결과, 가장 안쪽의 실린더에서 스퀴즈 필름 효과에 의해 상대적으로 높은 부가질량이 계산되었다. 분산곡선 예측결과 부가질량에 의해 가장 안쪽 실린더에서 주파수별파수의 크기가 높게 예측되었다. 주변 유체의 압력장을 비교해본 결과 산란파의 해를 적용한 압력장과 유한요소법의 수치해와 매우 유사하게 패턴이 형성되었다. 또한, 가진주파수가 증가할수록 복잡한 패턴의 압력장이 계산되었다. 예측된 압력장을 통해 다발체 내부의 실린더별 힘을 계산하였고, 이를 스펙트럴요소모델에 적용하였다. 실린더의 전달함수를 예측한 결과 개수가 증가할수록 일부 공진주파수에서 중첩모드가 발생되었고, 다른 모드에서는 입력파 파장이 구조물의 간격에 비해 길어서 중첩모드가 발생하지 않았다. 마지막으로 유한요소법과의 전달함수 비교 결과, 요소의 개수가 증가할수록 스펙트럴요소법으로 예측된 전달함수와 유사함을 알 수 있었다. 또한, 스펙트럴요소법은 유한요소법에 비해 적은 요소의 개수임에도 불구하고 전달함수가 정확하게 계산되었고, 위상차에 의한 중첩모드 형상을 반영하여 기존 방법에 비해 빠르게 예측할 수 있다. 이 연구결과를 통해 원자력 분야의 핵연료봉 다발체 진동해석 뿐만 아니라 수중 구조물의 예측기술 향상 및 강성설계 등으로 활용될 수 있다.

Acknowledgments

이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2019R1G1A109725213).

References

• Choi, M., Kang, H., Yoon, K. and Song, K., 2004, Vibration Analysis of A Dummy Fuel Rod Continuously Supported by Spacer Grids, Nuclear Engineering and Design, Vol. 232, No. 2, pp. 185~196. [https://doi.org/10.1016/j.nucengdes.2003.11.007]
• Dolfen, H., Bertocchi, F., Rohde, M. and Degroote, J., 2019, Vibrations in a 7-rod Bundle Subject to Axial Flow: Simulations and Experiments, Nuclear Engineering and Design, Vol. 353, Article no. 110227. [https://doi.org/10.1016/j.nucengdes.2019.110227]
• Bertocchi, F., Rohde, F., De Santis, D., Shams, A., Dolfen, H., Degroote, J. and Vierendeels, J., 2020, 3. Fluid-structure Interaction of a 7-rods Bundle: Benchmarking Numerical Simulations with Experimental Data, Nuclear Engineering and Design, Vol. 356, Article no. 110394. [https://doi.org/10.1016/j.nucengdes.2019.110394]
• Lee, U. and Oh, H., 2003, The Spectral Element Model for Pipelines Conveying Internal Steady Flow, Engineering Structures, Vol. 25, No. 8, pp. 1045~1055. [https://doi.org/10.1016/S0141-0296(03)00047-6]
• Lee, U. and Park, J., 2006, Spectral Element Modelling and Analysis of a Pipeline Conveying Internal Unsteady Fluid, Journal of Fluids and Structures, Vol. 22, No. 2, pp. 273~292. [https://doi.org/10.1016/j.jfluidstructs.2005.09.003]
• Lee, U. and Jang, I., 2012, Spectral Element Modeling and Analysis of the Blood Flows in Viscoelastic Vessels, Applied Mathematics and Computation, Vol. 218, No. 13, pp. 7295~7307. [https://doi.org/10.1016/j.amc.2012.01.008]
• Yang, W., Kang, H. and Park, J., 2020, Flexural Vibration Analysis of Nuclear Fuel Rod Bundles Interacting with Surrounding Fluid Subjected to Pressure Wave, Applied Sciences, Vol. 10, No. 7, p. 2282. [https://doi.org/10.3390/app10072282]
• Païdoussis, M. P., Price, S. J. and Langre, E., 2011, Fluid-structure Interactions Cross Flow Induced Instabilities, Cambridge, New York.
• Tian, W. X., Zhang, K., Hou, Y. D., Zhang, Y. P., Qiu, S. Z. and Su, G. H., 2016, Hydrodynamics of Two-phase Flow in a Rod Bundle Under Cross-flow Condition, Annals of Nuclear Energy, Vol. 91, pp. 206~214. [https://doi.org/10.1016/j.anucene.2016.01.025]
• Mohany, A. and Hassan, M., 2013, Modelling of Fuel Bundle Vibration and The Associated Fretting Wear in a CANDU Fuel Channel, Nuclear Engineering and Design, Vol. 264, pp. 214~222. [https://doi.org/10.1016/j.nucengdes.2012.08.039]
• Cho, S., Yang, W., Lee. S. and Park, J., 2016, Flexural Wave Cloaking Via Embedded Cylinders with Systematically Varying Thicknesses, Journal of Acoustical Society of America, Vol. 139, No. 6, pp. 3320~3324. [https://doi.org/10.1121/1.4950738]
• Cook, R., 2007, Concepts and Applications of Finite Element Analysis, John Wiley & Sons, Inc., New York.
• Park, Y. and Lee, D., 2020, Effects of Helicotrema Size in the Motions of Basilar Membrane with Consideration of Fluid-structure Interactions, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 5, pp. 425~431. [https://doi.org/10.5050/KSNVE.2020.30.5.425]