Variational Autoencoder를 이용한 데이터 및 지식기반 회전기기 이상 진단

1. 서 론

회전 기계는 동력 전달의 용이함과 에너지 변환의 간편함으로 인해 현대 산업 사회에서 없어서는 안 되는 기계이다. 이에 따라 회전 기계의 운전 신뢰성 확보는 국부적으로 기계 성능 유지에 따른 공정의 가동을 보증할 뿐만 아니라, 산업 전체적으로 경제성과 연결되어 있어서, 산업 경쟁력 향상의 중요한 요인이 되고 있다. 일반적으로 회전 기계는 윤활, 열화상 및 초음파 등 다양한 물리량에 의하여 기계 감시가 가능하지만, 회전 운동이라는 특징 때문에 진동에 의한 감시/진단 기술이 각광받아 왔다^(1,2). 단순히 진동의 실효치(크기)를 감시하는 기술부터 다양한 신호 처리 기법에 의해 효과적인 특징(feature)을 추출하여 감시 및 진단을 수행하는 다양한 기술이 개발되었다^(3~6).

이와 같은 기계 진단 기술에 신경망으로 대표되는 기계학습기법은 진단의 자동화라는 관점에서 20여 년 전부터 많은 시도가 있었으며, 성공적으로 산업에 적용되었다^(7~10). 최근 인공지능 기술의 급격한 발전에 힘입어 진동기반 기기 상태감시 및 진단 기술의 자동화를 위한 기계학습 기법의 새로운 전기가 마련되고 있으며, 다양한 기술개발이 진행되고 있다. 전문가에 의한 다양한 분석 및 경험을 이용해 효과적인 진동의 특징을 추출하고, 이를 기반으로 기기의 상태를 진단하고 예측하는 전통적인 방법에서 벗어나, 영상을 이용하거나 주파수 분석과 같은 간단한 분석결과만을 이상 진단 모델의 입력으로 사용하여 상태를 진단하는 기법들이 개발되고 있다⁽¹¹⁾.

Variational autoencoder(VAE)⁽¹²⁾는 데이터를 기반으로 새로운 데이터를 생성하는 모델의 하나로서, 학습 중 데이터의 차원을 축소하여 중요한 특징만을 자동적으로 추출하는 특성을 가지고 있다. 이와 같은 특성은 잘 학습된 VAE에 새로운 데이터를 입력으로 사용했을 때, 중요 특징 공간으로의 투영(projection)된 데이터를 출력으로 얻을 수 있도록 한다. 따라서 입력 데이터와 출력 데이터의 차이를 이용하여, 현재 측정 데이터가 학습에 사용된 데이터와 얼마나 다른지를 판단할 수 있고, 이를 기계 이상 진단에 직접적으로 적용 가능하다. 이와 같은 학습은 정상 데이터만으로 이상 진단을 수행할 수 있다는 장점을 지니고 있어서, 실제 고장 데이터 획득이 불가능한 대형 기계시스템의 진동기반 진단에 효과적으로 적용될 수 있다. 또한, VAE 학습 과정에서 입력과 출력에 대한 차이를 손실 함수(loss function)로 정의하는데, 이 손실 함수를 이상 점수(anomaly score)로 정의하면, 다차원(multi-dimensional) 데이터를 하나의 단일 지수로 변환하여 이상 진단을 수행할 수 있다.

이 논문에서는 VAE를 이용한 이상 진단의 절차를 설명하며, 이 때 이상 점수 정의 및 기준값 설정에 대하여 제안한다. 또한, VAE의 수학적 배경에 내재된 가중치 부가에 대한 원리를 설명하고, 이를 이용하여 데이터 기반만의 이상 진단이 아닌 전문가의 지식이 반영된 이상 진단 기술을 제안한다. 마지막으로 스팀터빈발전기에서 획득한 다채널 진동데이터를 이용하여, 제안된 이상 진단 기술을 적용하고 효용성을 보인다.

2. Variational Autoencoder(VAE)를 이용한 이상 진단

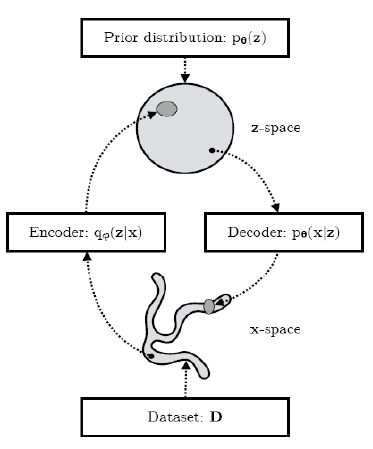
Variational autoencoder(VAE)는 기계학습의 데이터 생성 기법의 하나로서, Fig. 1과 같이^(1,3) 다차원 통계적(stochastic) 데이터를 은닉 변수(latent value)로 변환하는 인코더(encoder)와 은닉 변수를 다시 다차원의 데이터로 생성하는 디코더(decoder) 구조를 가지고 있다. 여기에서 은닉 변수도 입/출력 데이터와 마찬가지로 통계적 특성을 갖는 랜덤 변수(random variable)이다. 이와 같은 VAE는 일반적으로 어떤 다차원 데이터를 작은 차원으로 압축하고 다시 확장함으로써, 데이터의 중요하지 않은 부분은 제거하고 핵심적인 정보만을 갖는 부분만을 남기는 필터링의 역할을 할 수 있다. 이와 같은 특성을 이용하면, 다차원의 신호의 이상을 확인할 수 있으며, 기계 상태감시를 위한 이상 진단 방법으로 활용이 가능하다.

Fig. 1

Concept of variational autoencoder

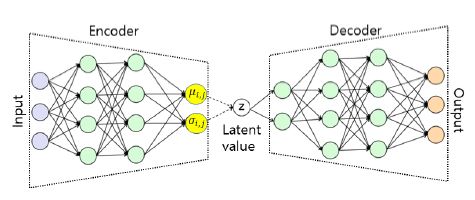
VAE 구조 중 Fig. 2의 인코더 부분과 디코더 부분은 해석적으로 풀기 어려운 구조(intractable)이며, 이에 수치적으로 이들을 다룰 수 있도록 가중치(weight)와 절편(bias) 및 활성화 함수(activation function)로 이루어진 신경망(neural network)으로 근사화하는 것이 일반적이다. 최근 신경망 기술의 고도화에 따라 다수의 층(layer)을 갖는 깊은(deep) 신경망 구조가 많이 사용되고 있으며, 이에 대한 자세한 사항은 참고문헌⁽¹²⁾에 설명되어 있다.

Fig. 2

Structure of variational autoencoder

VAE는 식 (1)과 같은 손실 함수를 최소화하여 모델을 얻을 수 있다.

여기에서 $$ -{{\rm E}}_{q_{\varphi }}\left[\mathrm{l}\mathrm{o}\mathrm{g}{p}_{\theta }\left(x_i|z\right)\right]$$는 Fig. 2의 입력(input)과 출력(output)의 오차(error)의 기댓값을 의미하며, $$ D_{KL}\left[q_{\varphi }\left(z|x_i\right)∣p_{\varphi }\left(z|x_i\right)\right]$$은 인코더의 실제 사후 확률 분포($$ p_{\varphi }\left(z|x_i\right)$$)와 근사화 확률 분포($$ q_{\varphi }\left(z|x_i\right)$$)의 유사한 정도를 나타내는 쿨백-라이블러 발산(Kullback-Leibler divergence)이다. 사전 확률 분포 및 출력의 확률 분포를 가우시안(Gaussian) 분포로 가정한다면, 식 (1)은 식 (2)로 변환할 수 있다.

여기에서 $$ {\mu }_{i,j}^{\text{'}}$$와 $$ {\sigma }_{i,j}^{\mathrm{2}\mathrm{\text{'}}}$$는 각각 출력 데이터의 평균 및 분산을 각각 의미하며, D는 입/출력 데이터의 차원(벡터 크기)이다. μ_i,j와 $$ {\sigma }_{i,j}^2$$은 은닉 변수의 평균과 분산이며, J는 은닉 변수의 차원을 각각 의미한다.

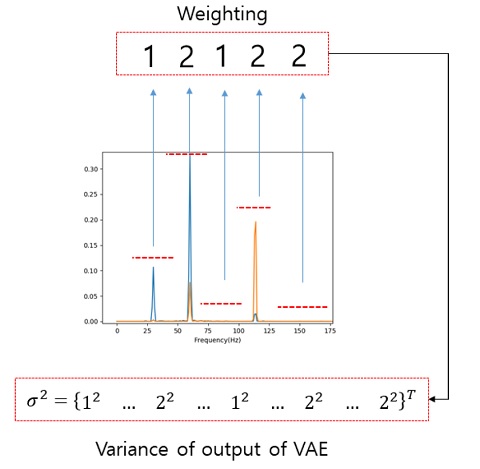
출력 데이터의 평균($$ {\mu }_{i,j}^{\text{'}}$$)은 일반적으로 일정값으로 정해질 수 있으나, 분산($$ {\sigma }_{i,j}^{\mathrm{2}\mathrm{\text{'}}}$$)은 VAE를 설계하는 과정에서 전문가가 그 값을 선택할 수 있다. 즉, 학습 데이터를 이용하여 VAE를 학습하는 과정에서 분산($$ {\sigma }_{i,j}^{\mathrm{2}\mathrm{\text{'}}}$$)을 임의로 조정할 수 있는 변수(user parameter)로 선정하여, 원하는 부분에 가중치를 부여할 수 있다. 이는 학습된 VAE가 출력(생성)하는 데이터의 분산을 임의로 결정할 수 있다는 것을 의미한다. 예를 들어 D차원을 갖는 데이터에서 전문가가 원하는 요소들에게 가중치를 부여하여, 이를 중요시 여기는 이상 진단 모델을 구축할 수 있는 것이다. 이는 VAE를 이용한 이상 진단 모델이 학습 데이터 기반으로 구축되지만, 전문가의 의도를 반영할 수 있다는 것을 의미한다. 이 논문에서는 입력 데이터로 진동 스펙트럼을 이용하는데, 미리 주요한 주파수 대역을 정하면, 이에 적절한 가중치(분산)를 선정하여, 진단 모델 학습 과정에서 손실 함수 정의에 반영할 수 있다(Fig. 3 참조). 이와 같은 방법은 데이터 기반이 주를 이루는 기계학습 기반 이상 진단 기술에 알려진 지식 또는 경험을 진단 모델에 추가할 수 있는 바탕이 된다.

Fig. 3

Weighting of spectrum in VAE

VAE를 이용한 이상 진단 모델이 정상 데이터만을 이용하여 학습되면, 식 (2)에서 정의된 손실 함수를 이상 점수(anomaly score)로 이용 가능하며, 이상 진단을 실시할 수 있다. 앞서 설명한 것과 같이, 손실 함수의 최소화는 학습(정상) 데이터와의 오차를 작게 만들고, 데이터의 확률 분포를 최대한 유사하게 만드는 것이기 때문에, 손실 함수의 값이 어떤 기준값 이상이 되면, 대상 기기에 이상이 있다고 판단할 수 있다. 기준값은 기존의 경험을 통해 절대적인 값을 이용할 수 있으나, 기기마다 설치 상태 및 외부 환경에 대한 고려가 필요하기 때문에, 시운전 기간 동안 데이터 수집 이후 기준값을 정하는 방법이 효과적이다. 특히, 이상 점수는 운전 조건 및 외부 요인에 따라 변하게 되고, 이와 같은 변화가 확률 분포를 이루기 때문에, 분포 형태를 고려하여 결정하는 것이 바람직하다.

학습(정상) 데이터를 이용한 이상 점수 분포는 데이터에 따라 다양한 형태를 가지고 있기 때문에 일반적인 분포를 정의하기 어렵다. 이에 다양한 확률 분포의 특성이 반영 가능한 편향된(skewed) 정규 분포의 형태의 Pearson type 3⁽¹⁴⁾의 확률 분포 함수로 곡선 맞춤을 실시한다. 정상 데이터를 학습 데이터로 이용했음을 고려하여, 누적 확률 분포(cumulative probability density)가 99.9 % 이상인 지점을 이상 기준값으로 결정할 수 있다. 마지막으로 측정데이터로부터 이상 점수를 산출하고, 기준값과 비교함으로서 이상 진단을 수행할 수 있다.

3. 스팀터빈 발전기 진동 특성

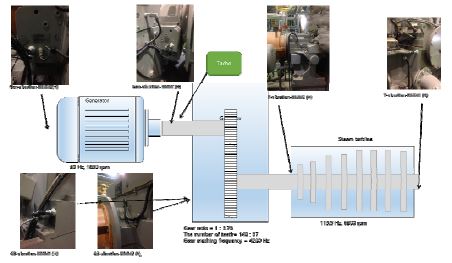
앞서 제안한 이상 진단 방법을 30 MW급 스팀터빈 발전기(Table 1 참조)에 진동(가속도)을 측정(Fig. 4참조)하여,하여, 이상을 진단하는 시스템에 적용했다. 스팀터빈 발전기는 보일러로부터 스팀을 공급받아 터빈에서 회전운동에너지를 생성하고, 이 회전운동을 감속기를 통하여 감속(토크 증가)시킨 후 발전기를 통하여 전기를 생산한다. 스팀터빈 발전기는 전기를 생산하는 일정 회전속도(발전기 기준 약 30 Hz)에서 동작하는 기기로서, 회전운동에 의한 진동이 효율적인 기기 감시 변수로서 사용되어 왔다. 진동의 측정 지점은 ISO 20816⁽¹⁵⁾에 기반하여, 각 부품의 베어링 부분으로 선정되었으며, 측정 물리량 또한 ISO 20816에 기반하여 진동 속도로 결정되었으며, 진동 속도 센서의 상세 제원은 Table 2와 같다.

Table 1

Specification of steam turbine generator

Fig. 4

Location of vibration sensors

Table 2

Specification of vibration sensor

Table 3

Direction of vibration sensors

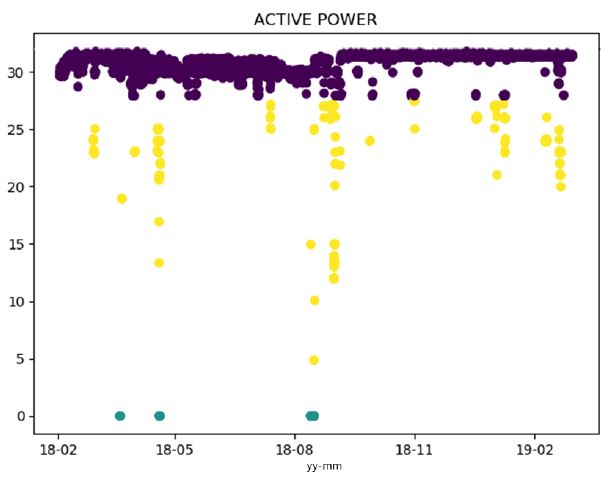
계절 변화가 기기에 미치는 영향을 고려할 수 있도록 데이터 획득은 2018년 2월부터 2019년 1월까지 1년 측정을 실시했으며, 진동 샘플링 주파수는 25600 Hz로 사용하여 약 10000 Hz까지 데이터를 확인할 수 있도록 했다. Fig. 5는 데이터 획득 기간 중 발전량을 나타낸 그림으로서, 30 MW 정격 운전이 실시된 구간과 감발(발전량을 낮춤) 구간을 확인할 수 있으며, 발전기가 정지된 구간도 확인할 수 있다. 이 연구를 통해 개발된 이상 진단 기법을 검증하기 위하여, 정격 운전 구간을 정상으로 가정했으며, 정격 이하의 발전이 이루어진 상황을 이상으로 가정했다.

Fig. 5

Power of steam turbine generator

이상 진단에 사용되는 VAE는 입력/출력 데이터로 측정 진동 데이터의 스펙트럼을 사용한다. 앞서 언급한 것과 같이 회전기계의 대표적인 특성들을 스펙트럼을 통해서 확인 가능하기 때문이다⁽¹⁾. 데이터 획득 장비로부터 측정된 원래 신호(raw data)는 푸리에(Fourier) 변환을 통해 주파수 영역의 스펙트럼으로 변환했다. 이 때, 터빈/기어/발전기의 회전 주파수, 기어 맞물림 주파수 또는 베어링의 특성 주파수 등을 고려하여, 1 Hz 간격의 주파수 해상도를 갖도록 데이터 처리를 수행했다.

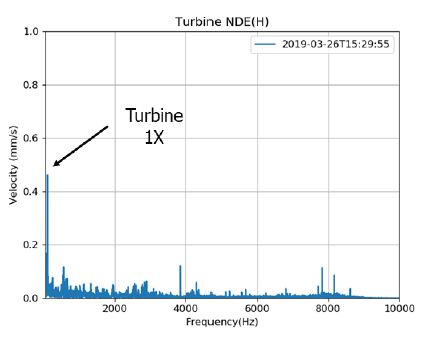
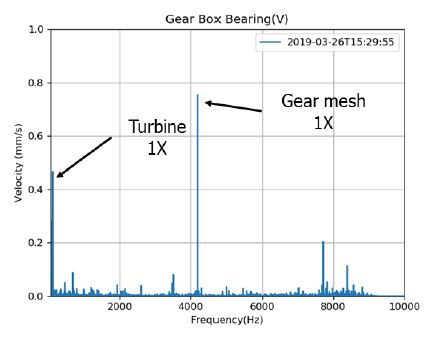
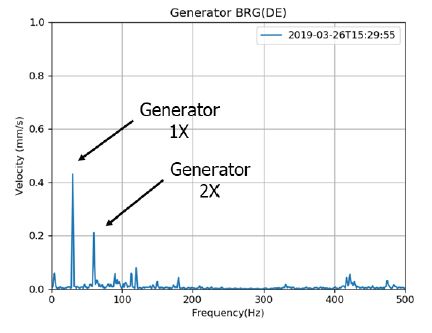
Figs. 6 ~ 8은 터빈, 감속기 및 발전기의 진동 스펙트럼을 각각 보여주고 있다. 터빈의 경우 회전 속도의 1차(6800 r/min, 113 Hz)의 성분이 주요 성분이며, 4000 Hz 이하에서 유동에 의한 광대역 진동이 관찰된다. 4000 Hz 부근에서 기어 맞물림 주파수(4200 Hz)의 측대역(sideband) 성분이 작게 나타나는 것을 볼 수 있는데, 이는 기어 맞물림 주파수에 터빈 회전속도가 변조되어 나타난 것이다. 이에 비해 감속기에서는 기어 맞물림 주파수(4200 Hz) 성분이 지배적으로 나타난다. 발전기는 회전속도의 1차(30 Hz), 2차(60 Hz)가 지배적이며, 이외의 주파수 성분은 거의 나타나지 않는다.

Fig. 6

Spectrum of turbine bearing

Fig. 7

Spectrum of gearbox bearing

Fig. 8

Spectrum of generator bearing

4. 스팀터빈 발전기 이상 진단

수집된 진동 스펙트럼은 VAE 학습의 효율성을 증가시키기 위하여, 학습 데이터 중 최대값을 이용하여 정규화(normalization)하고 입력 데이터로 사용했다. 이에 따라 VAE 입력은 61440(1 Hz ~ 10 240 Hz사이 1 Hz 해상도 스펙트럼 6채널)개이며, 인코더(encoder)와 디코더(decoder)가 각각 2개의 층을 갖고, 출력 또한 61440개의 스펙트럼을 갖는다. 활성화 함수로는 소프트플러스(softplus) 함수를 이용했으며, 각 층의 구조는 Table 4와 같다.

Table 4

Structure of variational autoencoder

이 논문에서는 진동 데이터로부터 나타나는 협대역 진동 특성을 모두 반영하기 위하여 1 Hz 해상도 스펙트럼을 입력으로 사용했으나, 대상 기기의 특성에 따라서 멜 스펙트럼(Mel spectrum), 옥타브밴드 파워 레벨, MFCC(Mel frequency cepstral coefficient) 등의 다양한 특징(feature)의 이용이 가능하다.

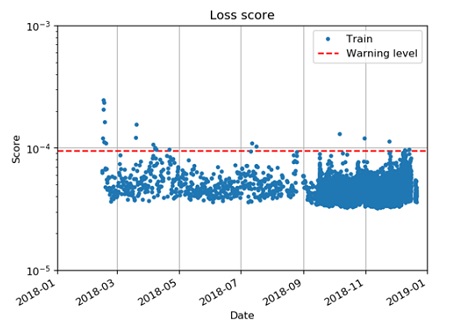
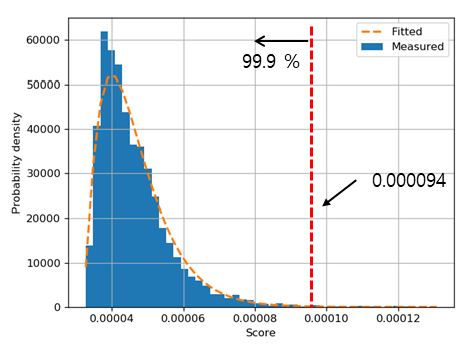
Fig. 9는 정상 데이터(30 MW 정격 출력, 4984개)를 이용하여 학습한 이후, 학습 데이터의 이상 점수(손실 함수 값)를 보여준다. 학습은 손실을 최소화하는 방향으로 진행되기 때문에 학습데이터에 대해서 일정한 크기의 이상 점수를 확인할 수 있으나, 각각 데이터의 국부적인 변화(기기 운전 조건의 미세한 변화)에 의하여, Fig. 10과 같은 분포를 갖게 된다. 이에 앞서 절에서 제안한 것과 같이 pearson type 3의 확률 분포로 곡선 맞춤을 실시했으며, 누적 확률 99.9 % 값을 이상 진단 기준치(0.00094)로 사용했다. Fig. 9를 보면, 정상 데이터임에도 불구하고 이상으로 분류되는 지점이 존재하나, 이상 진단의 보수적인 접근을 위하여, 위와 같이 99.9 %의 값을 기준치로 사용했다.

Fig. 9

Anomaly score(loss function) for training data

Fig. 10

Statistical distribution of loss function

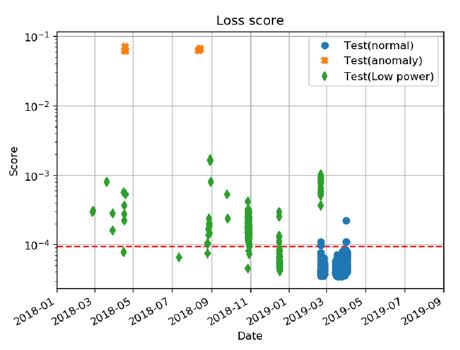
앞의 학습 데이터와는 다른 2019년 2월부터 2019년 5월까지 데이터 1061개를 시험(test) 데이터로 사용했으며, 2018년에 발전이 정지된 상태 및 감발 상태에서의 데이터(222개)를 이상으로 가정하여 시험을 진행했다. 그 결과를 Fig. 11과 Table 5에 각각 정리하였으며, 정확도 94.5 %로 이상 진단이 이루어졌음을 확인할 수 있다. 실제 정상인 데이터를 이상으로 분류하는 경우는 극히 적으나, 실제 이상(감발)의 경우를 정상으로 판단하는 경우가 많은 것을 확인할 수 있다. 이는 감발의 정도에 따라 정상 상태(정상 출력)와 유사한 상태가 존재하기 때문으로 판단된다.

Fig. 11

Anomaly score(loss function) for test data without weighting

Table 5

Confusion matrix of anomaly detection

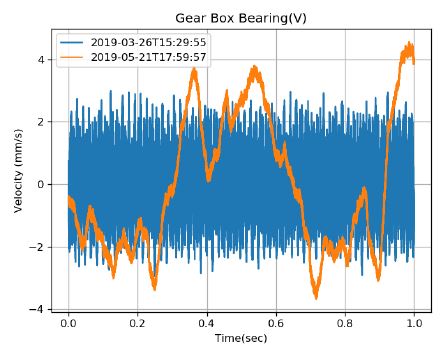
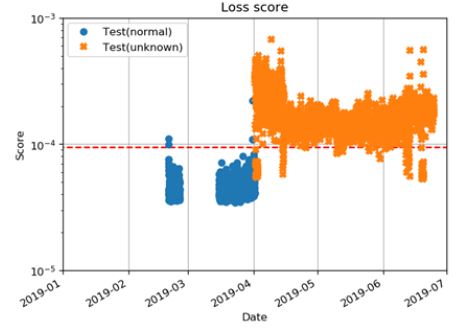
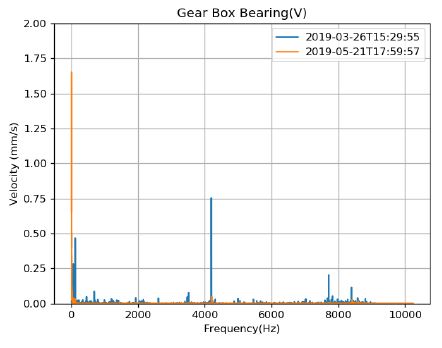
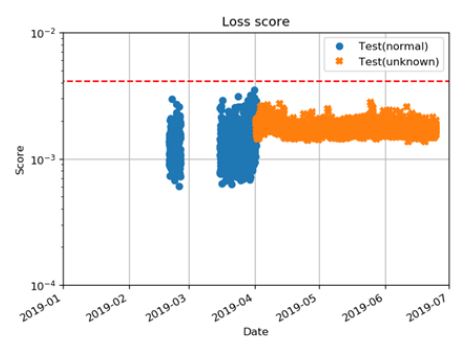
2019년 4월 이후 스팀터빈 발전기는 정상적인 운전을 지속했으나, Fig. 12와 같이 기어박스 수직 센서에 이상이 생긴 현상이 관찰되었다. 이 경우 센서 데이터 저주파수 성분으로 인해 Fig. 13과 같이 이상 점수가 크게 나타난다. 그러나 비록 센서의 문제로 인해 정상적인 신호가 들어오지 않았으나, Fig. 14와 같이 스펙트럼을 살펴보면 기어 맞물림 주파수(4200 Hz) 성분은 조금 측정이 되었음을 확인할 수 있다. 이에 따라 기어 맞물림 주파수 성분이 있는 3000 Hz ~ 5000 Hz 주파수 영역의 분산($$ {\sigma }_{i,j}^{2\text{'}}$$)을 0.1로 하여 그 주파수 영역의 가중치(3.16)를 높여서 학습 후 이상 진단을 실시하면, Fig. 15와 같이 정상으로 진단 결과가 나타남을 확인할 수 있다. Fig. 13과 15는 다른 손실 함수에 의해 학습되었으므로, 다른 확률 분포를 갖게 되고 서로 다른 이상 기준값이 도출되었다.

Fig. 12

Normal & abnormal vibration signals

Fig. 13

Anomaly score of abnormal sensor data without weighting

Fig. 14

Spectra of normal & abnormal sensors

Fig. 15

Anomaly score of abnormal sensor data with weighting

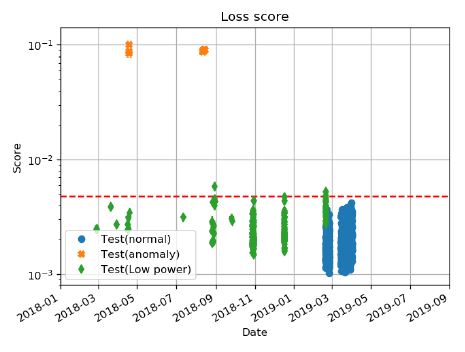
앞서 모든 주파수 대역에 같은 가중치를 준 결과(Fig. 11)와 달리, 3000 Hz ~ 5000 Hz 영역에 가중치를 3.16으로 주었을 때의 결과를 Fig. 16에 나타내었다. 앞서 Fig. 11과 유사하게 발전이 정지된 상태는 이상으로 가정했으며, 정상과 이상의 중간 상태라고 할 수 있는 감발 운전의 이상 진단 결과를 분석했다. 발전이 정지된 상태의 경우, 정상운전 때와의 차이가 명백하기 때문에 이상 점수가 Fig. 11과 Fig. 16에서 유사한 수준으로 나타나나, 감발 운전의 경우 가중치 부여에 따라 다른 이상 점수를 나타낸다.

Fig. 16

Anomaly score of test data with weighting

기어 맞물림 주파수 성분이 존재하는 대역에 가중치를 적용한 Fig. 16을 보면, 감발 상태도 정상 운전 상태로 판단하는 것을 확인할 수 있다. 이는 기어 맞물림 주파수 성분의 진동 크기는 감발에 따라 큰 차이가 없다는 것을 의미하며, 이에 따라 감발 운전 조건을 이상으로 가정하지 않을 때는 위와 같이 가중치를 줌으로서 감발 운전 조건을 정상으로 분류할 수 있음을 의미한다.

기존의 이상 진단에서 기준치를 설정하는 방법은 메이커의 자료 또는 기존의 기준치를 동일하게 사용하는 방식으로 물리적으로 그 기준치가 설정된 이유에 대한 분석이 부족했다. 이에 따라 기준치 변경 및 관리에 대한 체계적인 접근이 불가능하여, 과도한 오경보 및 이상 진단의 실패 사례가 많다. 이 논문에서 제시한 사용자 경험이나 논문에서 제시하는 가중치 부여 방식을 통하면, VAE와 같이 데이터 기반 진단 방법에 전문가의 경험과 물리적 의미를 추가하여 진단 모형을 만들 수 있으며, 이는 향후 더 정밀한 진단 및 복잡한 기계에 대한 진단에 효과적인 방법이 될 것으로 기대된다.

5. 결 론

진동을 이용한 기계시스템의 감시 및 진단은 다채널 데이터를 이용하여, 유용한 특징을 추출하고, 알려진 기준 또는 전문가의 경험을 기반으로 진단하는 방식으로 개발되어 왔다. 최근 기계학습 기법의 급격한 발전으로 인해, 손쉽게 빅데이터를 이용한 네트워크 기술 적용이 가능해 지고 있다. 이 논문에서는 variational autoencoder(VAE) 구조를 이용하여, 기계시스템의 이상을 진단하는 기술을 제안했다. 다채널 데이터를 하나의 이상 점수로 변환하고, 이를 감시함으로서 이상 발생의 유무를 확인할 수 있다. 또한, VAE에 내재된 가중치 적용을 통해서, 측정된 데이터에만 의존한 진단이 아닌 전문가 지식과 경험을 반영한 이상 진단 모델의 생성이 가능하다는 것을 보였다. 제안된 기술은 기계 상태에 대한 직관적인 감시에 유용할 것으로 판단되며, 조기 경보 및 잔여 수명 예측으로도 응용 가능할 것으로 기대된다.

Acknowledgments

이 연구는 2020년도 산업통상자원부의 재원으로 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구 과제(No. 20203010020010, 디지털 기반 해상풍력단지 통합 O&M 서비스 솔루션 개발 및 실증) 및 한국기계연구원 기관고유사업(인공지능 기반 기계 시스템 예측 진단 및 사고대응 기술 개발)의 결과입니다.

References

• Randall, R. B. 2011, Vibration-based Condition Monitoring: Industrial, Automotive and Aerospace Applications, Wiley, Chichester, U.K. [https://doi.org/10.1002/9780470977668]
• Shin, K. H., 2017, Development of Damage Indexes for Condition Monitoring of Rotating Machinery Using Vibration Signals and Its Application to a Large Centrifugal Compressor, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 7, pp. 915~923. [https://doi.org/10.5050/KSNVE.2017.27.7.915]
• Baek, D. J., Lee, Y.-B., Kim, S.-J., Kim, C. H. and Jang, G. H., 2003, A Fuzzy Expert System Based on Hybrid Database for Fault Diagnosis of Industrial Turbomachinery, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 13, No. 9, pp. 703~712. [https://doi.org/10.5050/KSNVN.2003.13.9.703]
• Park, S. T., Woo, H.-S., Won, J. I. and Park, S. B., 2012, Fault Detection of Rolling Element Bearing for Low Speed Machine Using Wiener Filter and Shock Pulse Counting, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 22, No. 12, pp. 1227~1236. [https://doi.org/10.5050/KSNVE.2012.22.12.1227]
• Lee, M. J., Jeon, J. Y., Kang, T., Han, S.-W. and Park, G., 2016, Application of Compressive Sensing and Statistical Analysis to Condition Monitoring of Rotating Machine, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 6, pp. 651~659. [https://doi.org/10.5050/KSNVE.2016.26.6.651]
• Ha, J. M., Ahn, B. H., Yu, H. T. and Choi, B. K., 2017, Feature Analysis based on Genetic Algorithm for Diagnosis of Misalignment, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 2, pp. 189~194. [https://doi.org/10.5050/KSNVE.2017.27.2.189]
• An, J. L., Han, Tain, Yang, B.-S., Jeon, J. and Kim, W. C., 2002, Fault Diagnostics Algorithm of Rotating Machinery Using ART-Kohonen Neural Network, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 12, No. 10, pp. 799~807. [https://doi.org/10.5050/KSNVN.2002.12.10.799]
• Lee, J. M., Hwang, Y., Kim, S.-J. and Song, C., 2003, Application of Hidden Markov Model Using AR Coefficients to Machine Diagnosis, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 13, No. 1, pp. 56~62. [https://doi.org/10.5050/KSNVN.2003.13.1.048]
• Han, H. S., Chong, U. P. and Cho, S., 2011, Neural-network-based Fault Detection and Diagnosis Method Using EIV(errors-in variables), Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 21, No. 11, pp. 1029~1035. [https://doi.org/10.5050/KSNVE.2011.21.11.1020]
• Ko, J., Choi, C. K., Kang, T., Han, S., Park, J. H. and Yoo, H. H., 2015, Fault Diagnosis of Rotating System Mass Unbalance Using Hidden Markov Model, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 25, No. 9, pp. 637~643. [https://doi.org/10.5050/KSNVE.2015.25.9.637]
• Sun, K. H., Huh, H., Tama, B. A., Lee, S. Y., Jung, J. H. and Lee, S., 2020, Vision-Based Fault Diagnostics Using Explainable Deep Learning with Class Activation Maps, IEEE Access, Vol. 8, pp. 129169~129179. [https://doi.org/10.1109/ACCESS.2020.3009852]
• Kingma, D. P. and Welling, M., 2013, Auto-encoding Variational Bayes, arXiv preprint arXiv 1312.6114, .
• Kingma, D. P. and Welling, M., 2019, An Introduction to Variational Autoencoders, arXiv preprint arXiv:1906.02691, . [https://doi.org/10.1561/9781680836233]
• Vogel, R. W. and McMartin, D. E., 1991, Probability Plot Goodness-of-fit and Skewness estimation Procedures for the Pearson Type 3 Distribution, Water Resources Research, Vol. 27, No. 12, pp. 3149~3158. [https://doi.org/10.1029/91WR02116]
• ISO 20816-1, 2016, Mechanical vibration - Measurement and Evaluation of Machine Vibration - Part 1: General Guidelines.