[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 31, No. 3, pp.298-307

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Jun 2021

Received 15 Feb 2021 Revised 08 Mar 2021 Accepted 15 Mar 2021

DOI: https://doi.org/10.5050/KSNVE.2021.31.3.298

PSO 알고리즘을 이용한 트랙킹 진동량 추정과 최적 제어기 설계

이문노^†

Estimation of Tracking Vibration Quantity and Optimal Controller Design Using a PSO Algorithm

Moonnoh Lee^†

Correspondence to: ^†Member, Dept. of Computer Engineering, Dong-Eui University, Professor E-mail : mnlee@deu.ac.kr ‡ Recommended by Editor Cheol Ung Cheong

Abstract

This paper presents a method for estimating the vibration quantity and designing a controller using a PSO algorithm for controlling the uncertainties of tracking actuator and disk reflectivity. After estimating the vibration quantity of an actual tracking loop through measurement, the proposed method calibrates the estimated vibration quantity by additionally reflecting the effect of the uncertainties. A minimum tracking loop gain can be appropriately modeled using the estimated vibration quantity. It can be applied to an H_∞ objective function to efficiently attenuate the tracking vibration and also to an objective function that prevents the tracking loop gain from becoming larger than necessary. An optimal tracking controller can be designed by minimizing the complementary objective functions using a PSO algorithm. The proposed estimation and design method is applied to a DVD track-following system and verified experimentally.

Keywords:

Track-following System, Tracking Vibration Quantity, Disk Reflectivity, Minimum Tracking Loop Gain, Robust H_∞ Objective Function, Particle Swam Optimization

키워드:

트랙 추종 시스템, 트랙킹 진동량, 디스크 반사율, 최소 트랙킹 루프 게인, 강인 H_∞ 목표 함수, 디스크 반사율, 입자 군집 최적화

1. 서 론

광디스크 드라이브나 플레이어의 트랙 추종 시스템은 광디스크의 편심적인 회전에 의해 발생하는 트랙킹 진동량에 대해 정밀한 트랙 추종을 위해 적절한 루프 게인을 가지도록 설계되어야 한다⁽¹⁾. 트랙킹 루프 게인이 너무 작으면 발생하는 트랙킹 진동을 효율적으로 제어할 수 없고 너무 크면 예기치 않은 작은 외란에도 광픽업이 목표 트랙을 벗어나 불안정해질 수 있다⁽²⁾. 그러면 트랙 추종 제어를 정상화한 후에 목표 트랙으로 다시 이동해야 하므로 광디스크 접근 시간은 증가하게 된다.

일반적으로 광디스크 표준에서 정의된 최대 진동량과 최대 진동 가속도를 토대로 최대로 발생될 수 있는 트랙킹 진동량을 계산할 수 있다^(1,3). 그러나 실제 드라이브에서는 이론적인 최대치보다 작은 크기와 주파수 범위의 트랙킹 진동량이 발생하기 때문에 설계된 트랙킹 루프는 필요 이상의 높은 게인을 가지게 된다. 그래서 실험을 반복하여 목표 성능을 만족할 때까지 제어기 파라미터를 조정하여야 한다.

트랙킹 진동량을 정확하게 추정할 수 있다면 목표 성능을 만족하는 트랙킹 루프 게인을 적절하게 설계할 수 있다. 특정한 드라이브에서 발생되는 트랙킹 진동량은 트랙킹 루프 조정 알고리즘을 토대로 추정할 수 있다^(4,5). 이 방법은 측정을 통해 특정 주파수에서의 트랙킹 루프의 위상이 목표 위상이 될 때까지 트랙킹 제어기의 DC 게인을 조정하고 조정된 결과를 트랙킹 진동량 추정에 사용하였다. 그러나 DC 보상 게인만을 조정하여 진동량을 추정하는 한계가 있고 디스크 반사율의 차이와 액추에이터 불확실성의 영향을 고려하지 않았기 때문에 특정 트랙킹 루프에서만 적용할 수 있다.

이 논문에서는 디스크 반사율과 트랙킹 액추에이터의 불확실성의 영향을 고려한 트랙킹 진동량 추정과 제어기 설계 방법을 제안한다. 실제 측정 데이터를 이용하여 특정 트랙킹 루프에 대한 진동량을 추정한 후에 디스크 반사율과 액추에이터의 불확실성의 영향을 추가로 반영하여 추정된 진동량을 보정한다. 제안된 진동량 추정 방법은 2단계로 구성되고 PSO(particle swarm optimization) 알고리즘을 적용하여 단계별 목표 함수를 최소화한다. 추정된 트랙킹 진동량을 토대로 최소 트랙킹 루프 게인을 모델링하고 트랙킹 진동 감쇠를 위한 H_∞ 목표 함수와 트랙킹 루프 게인이 필요 이상으로 커지지 않도록 하는 목표 함수를 설정하는데 적용한다. 설정된 목표 함수들은 복잡한 함수이기 때문에 PSO 알고리즘을 적용하여 목표 함수들을 최소화하는 트랙킹 제어기를 설계한다. 제안된 진동량 추정과 제어기 설계 방법은 DVD 트랙 추종 시스템에 적용하고 비교 실험을 통해 타당성을 검증한다.

2. PSO 알고리즘을 이용한 트랙킹 진동량 추정 방법

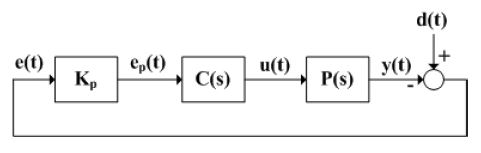
광디스크 드라이브나 플레이어는 광디스크에 초점을 맞추는 포커싱 제어를 실행한 후에 광픽업이 트랙 중심을 따라가는 트랙 추종 제어를 시작한다. Fig. 1은 트랙 추종 시스템의 블록도를 나타낸다.

Fig. 1

Block diagram of the track-following system

여기서 K_p는 증폭 게인, P(s)는 트랙킹 액추에이터, C(s)는 트랙킹 제어기를 나타낸다. 트랙킹 에러 e(t)는 트랙 중심과 빔스팟 사이의 차이를 나타내며 실제 드라이브에서는 게인 K_p에 의해 증폭된 에러 e_p(t)을 측정할 수 있다. 광디스크는 제조상의 차이로 디스크 반사율이 차이가 있기 때문에 디스크마다 증폭된 에러 e_p(t)의 진폭이 다를 수 있다. 디스크 반사율의 차이는 증폭 게인 K_p이 특정 영역의 불확실성을 가지는 것으로 표현할 수 있다.

K p = K p -, K p +, K p n = K p + + K p - / 2

(1)

광픽업이 트랙을 정밀하게 추종하기 위해 트랙킹 액추에이터는 voice-coil 모터를 사용하며 공칭 액추에이터 P_n(s)의 특성은 1차 공진주파수(f₀), 감쇠 상수(ξ), DC 감도(K_DC)를 사용하여 다음과 같이 근사화될 수 있다.

P n s = K D C 2 π f o 2 (1 - ξ 2) s 2 + 2 ξ 2 π f 0 s + 2 π f 0 2 1 - ξ 2

(2)

그리고 파라미터의 변화를 고려하여 계수 파라미터가 특정 영역의 불확실성을 가지는 것으로 트랙킹 액추에이터는 모델링될 수 있다.

P s = b 2 -, b 2 + s 2 + a 1 -, a 1 + s + a 2 -, a 2 +

(3)

광디스크의 편심 때문에 광디스크가 회전하면 수십 트랙 이상을 벗어날 수 있는 트랙킹 진동 d(t)이 발생한다. 트랙킹 진동은 디스크의 회전 주파수와 그 정수배의 주파수에서 상대적으로 큰 성분을 가진다. 각 주파수에서 발생하는 트랙킹 진동 성분 D(jω)은 Fig. 1로부터 증폭 게인, 트랙킹 에러, 트랙킹 제어기, 트랙킹 액추에이터에 의해 다음과 같이 나타낼 수 있다.

D j ω = = E j ω + Y j ω = 1 + K p C j ω P j ω E j ω = 1 + L j ω K p - 1 E p j ω

(4)

증폭 게인 식 (1)과 트랙킹 액추에이터 식 (3)은 불확실성을 포함하고 있기 때문에 각 주파수에서 발생하는 트랙킹 진동량을 직접적으로 계산할 수 없다. 그래서 식 (4)에 공칭 증폭 게인 K_pn, 공칭 액추에이터 모델 P_n(jω), 제어기 $C^j ω$ 를 적용하여 다음과 같이 트랙킹 진동량을 추정할 수 있다.

D^j ω = 1 + K p n C^j ω P n j ω K p n - 1 E p j ω

(5)

제어기 $C^j ω$ 는 진동량 추정 알고리즘에 의해 디스크 반사율과 액추에이터의 불확실성의 영향을 최대한 반영하도록 조정된다. 이 논문에서 제안하는 진동량 추정 알고리즘은 2단계로 구성된다. 먼저 측정된 데이터를 토대로 특정 트랙킹 루프에 대해 트랙킹 진동량을 추정한 후에 디스크 반사율과 액추에이터의 불확실성의 영향을 추가로 반영하여 추정된 진동량을 보정한다. 각 단계마다 적절한 목표 함수를 설정하고 PSO 알고리즘을 사용하여 목표 함수가 최소가 되는 제어기 $C^j ω$ 의 파라미터를 탐색한다.

2.1 특정 트랙킹 루프에 대한 진동량 추정

발생하는 트랙킹 진동량 식 (4)와 추정된 트랙킹 진동량 식 (5)의 차는 다음과 같이 나타낼 수 있다.

D j ω - D^j ω = L j ω - L^j ω E j ω L j ω = K p j ω C j ω P j ω, L^j ω = K p n C^j ω P n j ω

(6)

여기서 L(jω)는 트랙킹 루프 함수이고 $L^j ω$ 는 제어기 $C^j ω$ 이 적용된 공칭 트랙킹 루프 함수를 나타낸다. L(jω)는 디스크 반사율과 트랙킹 액추에이터의 불확실성 때문에 계산할 수 없지만 특정 드라이브에서는 트랙킹 루프 특성을 측정하여 진동량 추정에 사용할 수 있다.

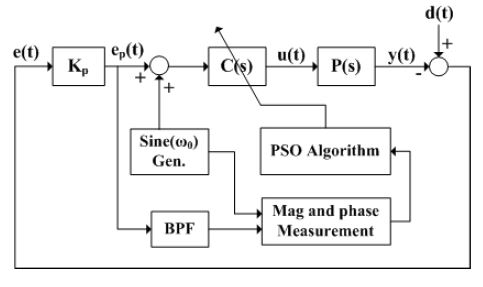
Fig. 2는 특정 트랙킹 루프에 대한 진동량 추정 블록도이다. 실제 드라이브의 트랙킹 루프 특성을 반영하기 위해 특정 주파수(ω₀)의 정현파 입력을 증폭된 에러 e_p(t)에 더하고 더한 출력을 트랙킹 제어기에 인가한다. 측정 노이즈와 루프 안정성을 고려하여 수백 Hz에서 제어 대역폭보다 낮은 주파수를 특정 주파수로 선택한다. 특정 주파수(ω₀) 성분만을 추출하기 위해 (0.9ω₀ < ω < 1.1ω₀) 대역만을 통과시키는 대역통과필터를 증폭된 에러에 연결한다. 측정 노이즈를 줄이기 위해 몇 주기 동안 특정 주파수(ω₀)의 정현파 입력 I(jω₀)와 대역통과필터의 출력 x(jω₀)사이의 진폭 비율(m)과 위상차(ϕ)을 측정하여 평균한다.

x j ω 0 I j ω 0 = L j ω 0 1 + L j ω 0 = m ∠ ϕ = a + j b

(7)

Fig. 2

Block diagram for estimating vibration quantity for a specific tracking loop

식 (7)을 전개하여 특정 주파수에서의 트랙킹 루프 함수 L(jω₀)를 구하고 게인 M(jω₀)과 위상 ϕ(jω₀)을 다음과 같이 계산한다.

L j ω 0 = a + j b 1 - a - j b = M j ω 0 ∠ ϕ j ω 0 M j ω 0 = a 2 + b 2 1 - a 2 + - b 2, ϕ j ω 0 = t a n - 1 b / a - t a n - 1 - b / 1 - a

(8)

L(jω)와 $L^j ω$ 는 선형 함수이기 때문에 특정 주파수에서 루프 게인과 위상이 거의 동일하면 L(jω)와 $L^j ω$ 의 루프 특성은 거의 동일하게 된다. 따라서 제어기 $C^j ω$ 를 조정하여 (L(jω₀)- $L^j ω 0$ )을 최소화하면 (D(jω)- $D^j ω$ )을 최소화할 수 있다.

L j ω 0 - L^j ω 0 = L j w 0 - K p n C^j ω 0 P n j ω 0

(9)

특정 주파수에 대해 측정한 트랙킹 루프 게인과 위상 식 (8)을 이용하여 식 (9)를 최소화하는 제어기 $C^j ω$ 을 구한다. 이를 위해 다음의 목표 함수 J_1e를 설정하고 J_1e를 최소화하는 제어기 $C^j ω$ 을 구하기 위해 식 (10)과 같이 PSO 알고리즘을 사용한다.

J 1 e = M j ω 0 - M^j ω 0 ϕ j ω 0 - ϕ^j ω 0 L^j ω 0 = K p n C^j ω 0 P n j ω 0 = M^j ω 0 ∠ ϕ^j ω 0

(10)

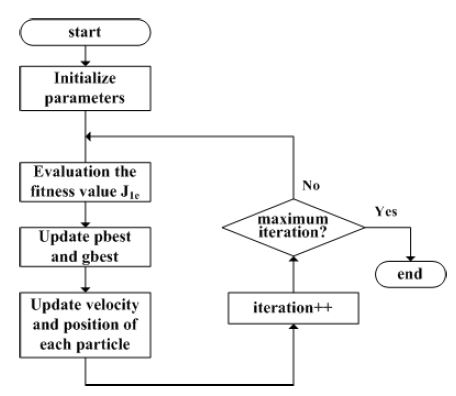
PSO 알고리즘은 일반적으로 새의 군집 행동 현상을 모방한 최적화 기법 중 하나이며, 비교적 쉽게 준최적해(sub-optimal solution)를 얻을 수 있다. PSO 기법은 계산 지능 최적화 방법 중에서 고속 처리, 구현의 용이성, 안정적인 수렴 특성을 가지고 있다. PSO 기법은 항상 전역적인 최적화를 보장하지는 않으나, 주어진 목표 함수 값이 최대한 작게 파라미터를 조정할 수 있다^(6~8). Fig. 3은 특정 트랙킹 루프의 진동량 추정을 위해 적용된 PSO 알고리즘의 흐름도이다.

Fig. 3

A flow diagram of a PSO algorithm for estimating vibration quantity

제어기 $C^j ω$ 의 파라미터를 최적화할 파라미터로 설정한다. 트랙킹 제어기는 보통 4차 이상이기 때문에 최적화할 파라미터 개수로 N_d=8을 설정하고 개체수 N_p와 최대 반복횟수 N_k를 설정한다. 진동량 추정을 위해 트랙 추종 제어를 실행해야 하므로 이를 위해 적용된 제어기의 파라미터 값을 토대로 위치의 최대값과 최소값을 설정한다.

각 개체에 대해 랜덤으로 초기 위치와 초기 속도를 생성하고 목표 함수 J_1e에 대한 적합도를 계산한다. 적합도가 최소가 되는 개체에 대해 Pbest_ij(Personal Best Position)와 Gbest_j(Global Best Position)값을 갱신하고 위치 X_ij(k)와 속도 V_ij(k)를 식 (11) ~ 식 (13)과 같이 업데이트한다^(6,7).

α = α m a x - α m a x - α m i n k N k

(11)

V i j k + 1 = α V i j k + c 1 × r a n d × P b e s t i j - X i j k + c 2 × r a n d × G b e s t j - X i j k

(12)

X i j k + 1 = X i j k + V i j k, i = 1, ⋯, N p, j = 1, ⋯, N d

(13)

여기서 양수 α는 반복횟수(k)에 따라 최대값 α_max에서 최소값 α_min로 변하는 가중치이고 양수 c₁와 c₂는 학습률을 나타낸다. rand는 [0,1]에서 균등하게 분포된 랜덤 숫자를 나타낸다. 종료 조건을 만족하거나 최대 반복횟수 N_k가 될 때까지 PSO 알고리즘을 반복한다. 종료 조건이 만족되면 각 파라미터의 최적화 값인 Gbest_j값에서 목표 함수식(10)을 최소화하는 제어기 $C^1 j ω$ 를 구할 수 있고 식 (5)에 대입하여 특정 트랙킹 루프에 대해 추정된 트랙킹 진동량을 계산할 수 있다.

D^1 j ω = 1 + K p n C^1 j ω P n j ω K p n - 1 E p j ω

(14)

2.2 디스크 반사율과 액추에이터 불확실성의 영향을 반영한 진동량 추정

앞 절에서 특정 드라이브의 트랙킹 루프에 대해 측정과 PSO 알고리즘을 이용하여 (D(jω)- $D^j ω$ )을 최소화되는 제어기 $C^1 j ω$ 를 구하여 트랙킹 진동량을 추정하였다. 그러나 트랙 추종 시스템은 디스크 반사율과 액추에이터의 불확실성이 존재하기 때문에 다른 드라이브의 트랙킹 루프에 측정 데이터식 (14)를 적용하면 추정 오차가 발생하게 된다. 모든 트랙킹 루프에 대해 측정을 통한 진동량 추정 방법을 적용할 수 없기 때문에 디스크 반사율과 액추에이터의 불확실성의 영향을 진동량 추정 방법에서 고려하여야 한다. 그래서 이 논문에서는 디스크 반사율과 액추에이터의 불확실성에 대해 트랙킹 루프 게인이 최대한 일정하게 유지하도록 하는 목표 함수를 추가로 고려하여 추정된 진동량을 보정한다.

불확실성을 포함하는 증폭 게인과 트랙킹 액추에이터의 곱 K_pP(s)는 분자와 분모 다항식으로 표현되므로 다음과 같이 Kharitonov 다항식을 가진다⁽⁹⁾.

K p P s = N s D s N 1^s = K p - b 2 -, N 2^s = K p + b 2 + D 1^s = s 2 + a 1 - s + a 2 -, D 2^s = s 2 + a 1 + s + a 2 - D 3^s = s 2 + a 1 - s + a 2 +, D 4^s = s 2 + a 1 + s + a 2 +

(15)

복소 평면의 경계를 토대로 증폭 게인과 일련의 극한(extreme) 액추에이터 모델을 반영한 극한 트랙킹 루프 함수는 Kharitonov 다항식 (15)를 사용하여 다음과 같이 구할 수 있다^(9,10).

L i s, δ = C s N l^s 1 - δ D j^s + δ D k^s ∪ C s 1 - δ N j^s + δ N k^s D l^s

(16)

여기서 δ=[0,1], (j,k)∈{(1,2),(1,3),(2,3),(3,4)}, l∈{1,2,3,4}이다. $N 1^s$ 과 $N 2^s$ 은 상수항만 있으므로 트랙킹 루프 함수 L(s)는 12개의 극한 트랙킹 루프 함수 L_i(s,δ)들을 가지게 된다. 그래서 δ=[0,1]에 대해 12개의 극한 트랙킹 루프 함수식 (16)을 고려하면 디스크 반사율과 액추에이터의 불확실성의 영향을 진동량 추정 방법에서 반영할 수 있다.

특정 트랙킹 루프에서 추정한 트랙킹 진동량식 (14)에서 디스크 반사율과 액추에이터의 불확실성을 반영하기 위해 다음의 목표 함수를 고려한다.

J 2 e = m a x i, δ 100 N ∑ k = 1 N M d j ω k - M i j ω k, δ M d j ω k × ϕ d j ω k - ϕ i j ω k ϕ d j ω k L d j ω k = K p n C^1 j ω k P n j ω k = M d j ω k ∠ ϕ d j ω k L i j ω k, δ = M i j ω k, δ ∠ ϕ i j ω k, δ, i = 1, ⋯, 12

(17)

목표 함수식 (17)은 특정 트랙킹 루프 함수 L_d(jω)와 12개의 극한 트랙킹 루프 함수 L_i(jω,δ)사이의 게인과 위상 차이의 곱으로 정의된다. 트랙킹 진동량이 발생하는 주파수 영역에 대해 N개의 주파수를 고르게 선택하고 각 주파수 ω_k에서 게인과 위상차의 곱을 구하여 평균한다. 식 (17)을 최소화하는 제어기 C(jω)을 구하기 위해 다음과 같이 Fig. 3의 PSO 알고리즘을 수정하여 사용한다.

트랙킹 제어기 파라미터를 최적화할 파라미터로 설정하고 추정된 제어기 $C^1 j ω$ 의 파라미터 값을 토대로 위치의 최대값과 최소값을 설정한다. 각 개체에 대해 랜덤으로 초기 위치와 초기 속도를 생성하고 목표 함수 J_2e에 대한 적합도를 계산한다. 적합도가 최소가 되는 Pbest_ij와 Gbest_j값을 갱신하고 위치와 속도를 업데이트한다. 종료 조건이나 최대 반복횟수를 만족하면 PSO 알고리즘이 종료되고 각 파라미터의 최적화 값인 Gbest_j값에서 목표 함수식 (17)을 최소화하는 제어기 $C^2 j ω$ 를 구하고 식 (5)에 대입하면 디스크 반사율과 액추에이터의 불확실성의 영향을 반영한 트랙킹 진동량을 구할 수 있다.

D^j ω = 1 + K p n C^2 j ω P n j ω K p n - 1 E p j ω

(18)

3. 추정된 트랙킹 진동량을 이용한 최적 제어기 설계

트랙 추종 시스템은 트랙킹 진동과 디스크 반사율과 액추에이터의 불확실성에 대해 트랙킹 에러가 최대 허용 에러 e_max보다 작게 유지되도록 제어하여야 한다. 이를 위해 트랙킹 진동량을 최대한 정확하게 추정하고 트랙킹 루프 게인이 최소 트랙킹 루프 게인보다 크게 설계한다⁽¹⁾. 이 논문에서는 추정된 트랙킹 진동량식 (18)을 목표 성능을 만족하는 트랙킹 제어기 설계에 사용한다. 최소 트랙킹 루프 게인 L_min(jω)은 추정된 트랙킹 진동량식 (18)과 최대 허용 에러 e_max로부터 다음의 식을 만족하는 함수 형태로 모델링될 수 있다.

L m i n j ω ≥ D^j ω e m a x

(19)

트랙킹 루프 게인 L(jω)이 L_min(jω)보다 크면 각 주파수에서 트랙킹 에러는 식 (20)과 같이 e_max보다 작게 된다.

E j ω = D j ω 1 + L j ω ≤ D^j ω 1 + L m i n j ω ≤ D^j ω L m i n j ω ≤ e m a x

(20)

식 (19)에서 모델링한 L_min(jω)은 트랙킹 진동 감쇠를 위해 강인 H_∞ 제어 알고리즘의 가중 함수로 사용될 수 있다. 강인 H_∞ 목표 함수는 다음과 같이 정의될 수 있다^(11,12).

J 1 c = m a x i, δ L m i n j ω 1 1 + L i j ω, δ ∞

(21)

여기서 i=1,…,12이고 δ=[0,1]이다. J_1c이 1보다 작으면 트랙 추종 시스템은 강인 안정하고 트랙킹 진동과 디스크 반사율과 액추에이터의 불확실성에 대해 트랙킹 에러가 e_max보다 작게 된다. 목표 함수식(21)을 최소화하는 트랙킹 제어기는 최적화 알고리즘을 사용하여 구할 수 있다. 그러나 식 (21)이 작은 값을 가질수록 트랙킹 루프는 더 높은 게인을 가지게 된다. 일반적으로 트랙킹 루프는 적절한 게인을 가져야 하며 필요 이상으로 루프 게인이 크면 예기치 않은 작은 고주파 외란에도 높은 제어기 출력을 만들어내어 광픽업이 목표 트랙을 벗어나 불안정해질 수 있다. 이러한 트랙 추종 제어의 특성을 반영하여 다음과 같이 N개의 주파수 ω_k에서 극한 트랙킹 루프 게인 L_i(jω_k,δ)과 최소 트랙킹 루프 게인 L_min(jω_k)의 차이의 평균을 최소화하는 다음의 목표 함수를 고려한다.

J 2 c = m a x i, δ 1 N ∑ k = 1 N L i j w k, δ - L m i n j ω k L m i n j ω k

(22)

목표 함수식 (21)과 식 (22)는 서로 반대되는 특성을 가지기 때문에 J_1c이 작은 값을 가질수록 J_2c는 큰 값을 가진다. 상호보완적인 목표 함수식 (21)과 식 (22)를 통해 트랙킹 루프가 적절한 루프 게인을 가지도록 하기 위해 다음의 적합도 함수를 사용한다.

J 2 = λ 1 J 1 c + λ 2 J 2 c

(23)

여기서 λ₁과 λ₂는 목표 함수식 (21)과 식 (22)에 대한 가중치이다. PSO 알고리즘을 적용하면 J_1c < 1을 만족하면서 적합도 함수 J₂를 최소화하는 트랙킹 제어기를 설계할 수 있다. 다음은 트랙킹 제어기 설계를 위한 PSO 알고리즘을 나타낸다.

Step 1: 개체수 N_p, 최적화할 파라미터 개수 N_d=8, 반복횟수 N_k를 초기화한다. 최적화할 각 파라미터의 최대값과 최소값을 설정한다.

Step 2: 각 개체에 대해 랜덤으로 초기 속도와 초기 위치를 생성한다. 생성된 위치로부터 트랙킹 제어기를 구성하고 J_1c을 계산하여 J_1c < 1인 개체만 초기 개체로 설정한다.

Step 3: 각 개체에 대해 목표 함수 J_1c과 J_2c을 계산하고 적합도 함수식 (23)을 계산한다.

Step 4: J_1c < 1를 만족하면서 적합도 함수가 최소가 되는 개체에 대해 Pbest_ij와 Gbest_j값을 갱신한다.

Step 5: 위치와 속도를 식 (11), 식 (12), 식 (13)에 의해 새롭게 업데이트한다.

Step 6: 종료 조건이 만족되지 않거나 최대 반복 횟수가 아니면 Step 3으로 가서 계속 수행한다. 종료 조건을 만족하면 최적화된 각 파라미터 값인 Gbest_j값을 통해 트랙킹 제어기를 구한다.

이 논문에서는 디스크 반사율과 액추에이터의 불확실성의 영향을 반영하여 트랙킹 진동량식 (18)을 추정하고 이를 토대로 최소 트랙킹 루프 게인을 모델링하고 목표 함수식 (21)과 식 (22)에 적용한다. 그리고 PSO 알고리즘을 적용하여 식 (23)을 최소화하는 트랙킹 제어기를 설계함으로써 트랙킹 에러는 최대 허용 에러보다 항상 작게 유지되고 트랙킹 루프 게인이 필요 이상으로 커지지 않게 된다.

4. 실험 결과

제안된 진동량 추정과 제어기 설계 방법을 검증하기 위해 DVD 트랙 추종 시스템에 적용하였다. 트랙킹 루프의 진폭과 위상을 측정하기 위해 필요한 실험 환경을 구현하였고 진동량 추정 알고리즘, PSO 알고리즘, 제어기 설계 알고리즘은 MATLAB를 사용하여 구현하였다.

Fig. 4는 트랙킹 루프 측정을 위한 실험 환경으로 광디스크 드라이브, DAQ 보드, 아날로그 회로로 구성된다. DAQ 보드는 50 kHz의 주파수로 증폭된 에러 e_p(t)를 측정하고 DAC를 통해 2 kHz의 정현파 입력 I(jω₀)를 출력한다. 그리고 DAQ 보드의 CVI 프로그램을 통해 1.8 kHz∼2.2 kHz 주파수만을 통과시키는 디지털 대역통과필터를 구현한다. 아날로그 회로는 출력된 정현파 입력과 증폭된 에러를 더하여 광디스크 드라이브에 인가한다.

Fig. 4

An experimental environment for a tracking loop measurement

실험에서 사용되는 트랙킹 액추에이터는 1차 공진 주파수 65 Hz, 감쇠 상수 0.158, DC 감도 0.95 mm/V이고 10 % 범위의 파라미터 불확실성을 고려하여 다음과 같이 모델링하였다.

P s = 150.6, 166.5 s 2 + 122.7, 135.6 s + 158460, 175140

(24)

실험 환경에서 0.37 ㎛의 트랙킹 에러가 1.2V로 변환되므로 공칭 증폭 게인 K_pn은 3.24×10⁶[V/M]이고 10 %의 디스크 반사율의 차이를 고려하여 증폭 게인은 식 (25)와 같이 나타낼 수 있다.

K p = 3.08 × 106, 3.40 × 106

(25)

실험에서는 제안된 진동량 추정 방법과 트랙킹 루프 조정을 통한 진동량 추정 방법^(4,5)의 성능을 비교하기 위해 DVD 12X에서 진동량을 추정하였다.

특정 트랙킹 루프에 대한 트랙킹 진동량을 추정하기 위해 인가된 2 kHz의 정현파 입력과 대역통과필터의 출력 x(jω₀)사이의 진폭 비율(m)과 위상차(ϕ)를 5주기 동안 측정하여 평균하였다. 그리고 식 (7)과 식 (8)을 통해 특정 주파수에서의 루프 게인 M(jω₀)=3.3과 위상 ϕ(jω₀)=-143°을 구하고 이를 토대로 목표 함수 J_1e를 식 (26) 같이 설정하였다.

J 1 e = 3.3 - M^j w 0 - 143 ° - ϕ^j w 0

(26)

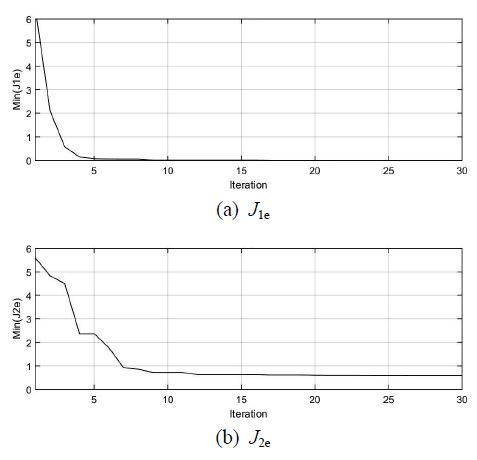
Fig. 3의 PSO 알고리즘을 적용하기 위해 개체수 N_p=10, 파라미터 개수 N_d=8, 최대 반복횟수 N_k=30, α_min=0.1, α_max=0.2, c₁=c₂=0.5를 설정하였다. Fig. 5(a)는 각 반복횟수에서 목표 함수 J_1e의 최소값을 나타낸다.

Fig. 5

The minimum values of the objective functions

목표 함수 (26)을 최소화하는 제어기 $C 1^s$ 는 다음과 같다.

4.7 × 106 s 3 + 4.9 × 1011 s 2 + 5.7 × 1015 s + 1.8 × 1019 s 4 + 4.6 × 105 s 3 + 1.9 × 1011 s 2 + 6.5 × 1015 s + 4.1 × 1018

(27)

공칭 액추에이터 모델, 공칭 증폭 게인, 트랙킹 에러, 제어기식 (27)을 식 (14)에 대입하면 특정 드라이브에서 발생하는 트랙킹 진동량을 추정할 수 있다.

디스크 반사율과 액추에이터의 불확실성의 영향을 반영하기 위해 식 (24)와 식 (25)를 식 (15)에 대입하여 극한 트랙킹 루프 함수 L_i(s,δ)를 구하고 목표 함수 J_2e를 다음과 같이 설정하였다.

J 2 e = m a x i, δ 13 ∑ k = 1 300 M d j ω k - M i j ω k, δ M d j ω k × ϕ d j ω k - ϕ i j ω k ϕ d j ω k

(28)

0 Hz ∼10 kHz 주파수 영역에서 300개의 주파수를 고르게 선택하여 각 주파수 ω_k에서 특정 트랙킹 루프 함수 L_d(jω_k)와 12개의 극한 트랙킹 루프 함수 L_i(kw_k,δ)사이의 게인과 위상차의 곱을 구하여 평균하였다. 목표 함수 J_2e를 최소화하는 PSO 알고리즘을 적용하기 위해 N_p=10, N_d=8, N_k=30, α_min=0.3, α_max=0.5, c₁=c₂=1.0를 설정하였다. Fig. 5(b)는 각 반복횟수에서 목표 함수 J_2e의 최소값을 나타낸다. PSO 알고리즘을 종료한 후에 J_2e의 최소값은 0.5840이고 식 (28)을 최소화하는 제어기 $C 2^s$ 는 다음과 같다.

6.0 × 106 s 3 + 4.2 × 1011 s 2 + 3.9 × 1015 s + 1.6 × 1019 s 4 + 7.4 × 105 s 3 + 2.7 × 1011 s 2 + 5.7 × 1015 s + 3.8 × 1018

(29)

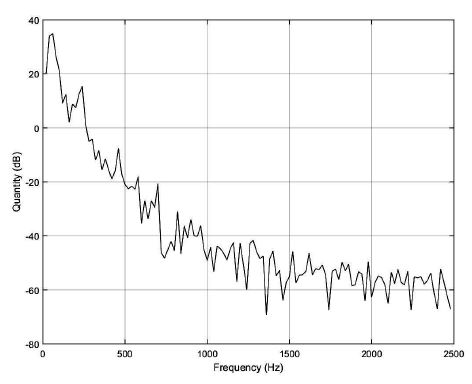
식 (29)를 식 (18)에 대입하면 디스크 반사율과 액추에이터의 불확실성의 영향을 반영한 트랙킹 진동량 $D^j ω$ 을 추정할 수 있다. Fig. 6은 제안된 트랙킹 추정 방법을 통해 DVD 12X에서 추정된 트랙킹 진동량을 나타낸다.

Fig. 6

The estimated tracking vibration quantity on DVD 12X

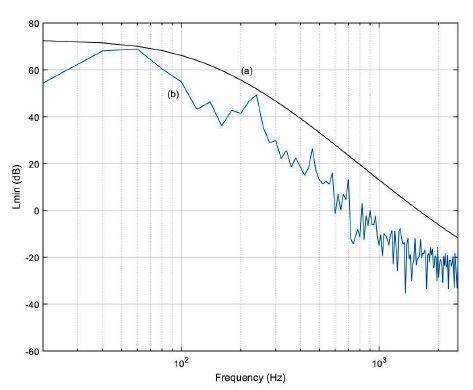
제안된 진동량 추정 방법의 타당성을 검증하기 위해 트랙킹 루프 조정을 통한 진동량 추정 방법과 비교하였다. Fig. 7의 (a)는 제안된 방법에 의해 추정된 진동량을 나타내고 Fig. 7의 (b)는 트랙킹 루프 조정 방법에 의해 추정된 진동량을 나타낸다. 디스크 반사율과 트랙킹 액추에이터의 불확실성이 영향을 미치는 저주파 영역에서 제안된 방법에 의해 추정된 진동량이 상대적으로 더 크다는 것을 알 수 있다.

Fig. 7

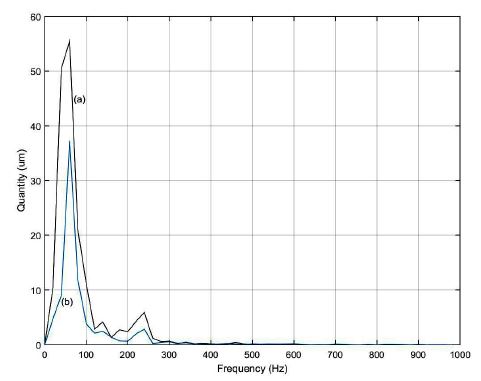
The tracking vibration quantities estimated by the proposed method (a) and the loop gain adjustment method (b)

추정된 트랙킹 진동량을 토대로 최소 트랙킹 루프 게인을 모델링하기 위해 e_max=0.03를 설정하였다. Fig. 8의 (a)와 (b)는는 최소 트랙킹 루프 함수 L_min(s)와 $D^s$ /e_max의 주파수 특성을 나타낸다. 최소 트랙킹 루프 함수 L_min(s)는 각 주파수에서 $D^s$ /e_max보다 게인이 크도록 다음과 같이 적절한 함수로 모델링하였다.

605 s 3 + 4.9 × 107 s 2 + 1.1 × 1012 s + 5.8 × 1015 s 4 + 5.0 × 103 s 3 + 8.3 × 106 s 2 + 5.6 × 109 s + 1.3 × 1012

(30)

Fig. 8

The Bode plots of the minimum tracking loop function (a) and D^s/emax (b)

발생되는 트랙킹 진동과 디스크 반사율과 액추에이터의 불확실성에 대해 트랙킹 에러가 최대 허용 에러보다 항상 작게 유지되고 예기치 않은 고주파 외란에도 불안정해지지 않도록 하기 위해 식 (30)을 식 (21)과 식 (22)의 목표 함수 J_1c과 J_2c에 적용하였다. J_2c에서는 제어 대역폭을 고려하여 0 Hz ∼5 kHz 범위의 100개의 주파수를 고르게 선택하였다.

J 2 c = m a x i, δ 1100 ∑ k = 1 100 L i j ω k, δ - L m i n j ω k L m i n j ω k

(31)

PSO 알고리즘을 위해 N_p=15, N_d=8, N_k=30, α_min=0.4, α_max=0.9, c₁=c₂=2.0을 설정하였고 적합도 함수 J₂는 J_1c과 J_2c의 중요도를 고려하였다.

J 2 = J 1 c + 0.5 J 2 c

(32)

PSO 알고리즘이 종료된 후 J_1c의 최소값은 0.906이고 J_2c의 최소값은 1.93이다. J_1c < 1을 만족하면서 적합도 함수 J₂를 최소화하는 트랙킹 제어기 C(s)는 다음과 같다.

5.7 × 106 s 3 + 2.4 × 1011 s 2 + 2.5 × 1015 s + 1.5 × 1019 s 4 + 6.9 × 105 s 3 + 2.3 × 1011 s 2 + 3.3 × 1015 s + 6.3 × 1018

(33)

Fig. 9(a)와 Fig. 9(b)는 설계된 트랙킹 루프 함수와 최소 트랙킹 루프 함수의 주파수 특성을 나타낸다. 목표 함수 J_1c이 1보다 너무 작지 않고 목표 함수 J_2c이 최소가 되도록 설계되었기 때문에 트랙킹 루프 게인이 최소 트랙킹 루프 게인보다 크지만 필요 이상으로 너무 크지 않는 것을 볼 수 있다.

Fig. 9

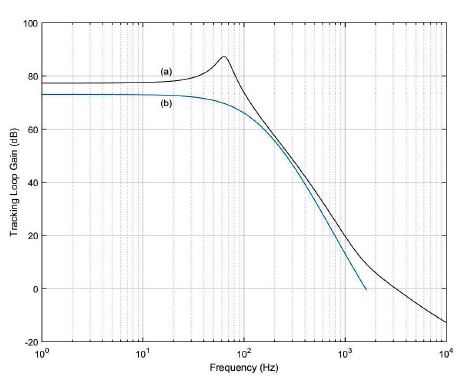
The Bode plots of the designed tracking loop function (a) and the minimum tracking loop function (b)

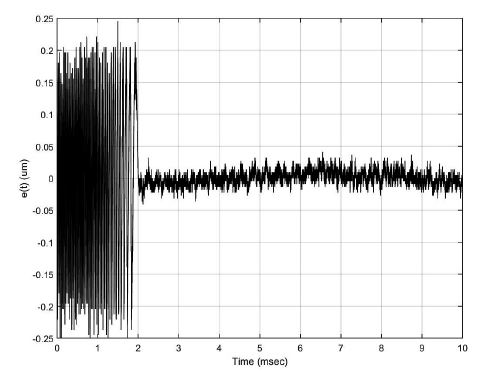
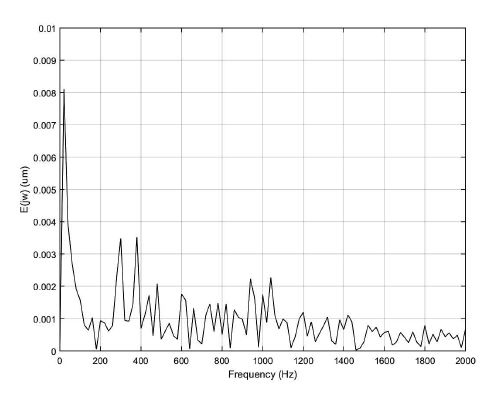
Fig. 10은 설계된 트랙킹 제어기를 트랙 추종 시스템에 적용하기 전과 후의 트랙킹 에러를 나타낸다. 트랙킹 제어를 시작하기 전에는 발생하는 트랙킹 진동에 의해 광픽업이 1 트랙을 지나갈 때마다 트랙킹 에러에 정현파가 출력된다. 그러나 트랙킹 제어기를 적용한 2 ms 이후에는 트랙킹 에러가 트랙 중심에서 최대 허용 에러 ±0.03 ㎛ 이내에서 유지되는 것을 볼 수 있다. Fig. 11은 트랙킹 제어기가 적용된 후의 트랙킹 에러의 주파수 특성을 나타낸다. 저주파에서 상대적으로 큰 주파수 성분을 가지지만 모든 주파수에서 ±0.03 ㎛보다 더 작은 값을 가지는 것을 볼 수 있다.

Fig. 10

The tracking error before and after applying the designed tracking controller

Fig. 11

The Bode plot of the tracking error after a designed controller is applied

5. 결 론

이 논문에서는 디스크 반사율과 액추에이터의 불확실성의 영향을 고려한 트랙킹 진동량 추정 방법을 제안하였고 추정된 진동량을 토대로 트랙킹 제어기를 설계하였다. 특정 드라이브의 트랙킹 루프에 대해 진동량을 추정한 후에 디스크 반사율과 액추에이터의 불확실성의 영향을 추가로 반영하여 추정된 진동량을 보정하였다. 제안된 진동량 추정 방법은 단계별 목표 함수를 최소화하기 위해 PSO 알고리즘을 사용하였다. 추정된 트랙킹 진동량을 토대로 최소 트랙킹 루프 함수를 모델링하였고 강인 H_∞ 목표 함수와 루프 게인이 필요 이상으로 커지지 않도록 하는 목표 함수에 사용하였다. 그리고 PSO 알고리즘을 적용하여 목표 함수들을 최소화하는 트랙킹 제어기를 설계하였다. 제안된 진동량 추정과 제어기 설계 방법은 DVD 트랙 추종 시스템에 적용하였고 실험을 통해 타당성을 검증하였다.

Acknowledgments

이 논문은 2019학년도 동의대학교 연구년 지원에 의하여 연구되었음.

References

Jin, K. B. and Lee, M.-N., 2003, Vibration Control Technology of an Optical Disk Drive, Journal of the KSNVE, Vol. 13, No. 1, pp. 48~55.
Yen, J. Y., Wang, F. J. and Chen, Y. Y., 1993, A Fuzzy Scheduling Controller for a Computerdisk File Track Following Servo, IEEE Transactions on Industrial Electronics, Vol. 40, No. 2, pp. 266~272. [https://doi.org/10.1109/41.222649]
Choi, J.-Y., Jun, H.-G., Chun, C.-H., Lee, M.-N., Yang, H.-S. and Park, Y.-P., 2002, Disturbance Measurement of Optical Disc and Servo Loop Design Related to Its Result, Proceedings of the International Conference on Motion and Vibration Control 6.1, pp. 326~332. [https://doi.org/10.1299/jsmeintmovic.6.1.326]
Lee, M.-N., Jin, K. B. and Lee, J. K., 2005, Estimation of Tracking Vibration Quantity for an Optimal Tracking Controller Design, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 15, No. 5, pp. 578~585. [https://doi.org/10.5050/KSNVN.2005.15.5.578]
Lee, M.-N. and Jin, K. B., 2008, A Controller Design Method for Constructing a Robust Track-following System, IEEE Transactions on Consumer Electronics, Vol. 54, No. 2, pp. 538~544. [https://doi.org/10.1109/TCE.2008.4560127]
Kennedy, J. and Eberhat R., 1995, Particle Swarm Optimization, Proceedings of ICNN’95 International Conference on Neural Networks IEEE, Vol. 4, pp. 1942~1948.
Shin, J.-H. and Lee, M., 2020, Pso-based Adaptive Neural Control for Trajectory Tracking of a Mobile Robot, Journal of Control, Automation, and System Engineering, Vol. 26, No. 6, pp. 506~516. [https://doi.org/10.5302/J.ICROS.2020.20.0052]
Li, S.-A., Hsu, C.-C., Wong. C.-C. and Yu, C.-J., 2011, Hardware/Software Co-design for Particle Swarm Optimization Algorithm, Information Sciences, Vol. 181, No. 20, pp. 4582~4596. [https://doi.org/10.1016/j.ins.2010.07.017]
Hsu, C.-C., Chang, S.-C. and Yu, C.-Y., 2007, Tolerance Design of Robust Controllers for Uncertain Interval Systems Based on Evolutionary Algorithms, IET Control Theory and Applications, Vol. 1, No. 1, pp. 244~252. [https://doi.org/10.1049/iet-cta:20050300]
Bhattacharyya, S. P., Chapellat, H. and Keel, L., 1995, Robust Control – the Parametric Approach, Upper Saddle River, New Jersey, Prentice Hall. [https://doi.org/10.1016/B978-0-08-042230-5.50016-5]
Zhou, K., Doyle, J. C. and Glover, K., 1996, Robust and Optimal Control, Upper Saddle River, New Jersey, Prentice Hall.
Doyle, J. C., Francis, B. A. and Tannenbaum, A. M., 1992, Feedback Control Theory, Macmillan, New York.

Moonnoh Lee received the B.S. degree in electronic engineering from Kyungpook National University in 1991, the M.S. and the Ph.D. degrees in electrical engineering from KAIST in 1993 and 1998. From 1998 to 2001, he worked for Samsung Electronics Co. as a senior research engineer. Since 2001, he has been with Department of Computer Engineering at Dong-Eui University, where he is currently a full professor. His research interests include robust control, optimal control, embedded systems, and intelligent systems.