요요 진동에너지 하베스터의 파력발전 적용에 관한 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
This study focuses on a yo-yo vibrational energy harvester tuned to a low frequency, which is common among ocean waves. The proposed device can be installed inside a buoy and is, thus, protected from the harmful marine environment. It is demonstrated that the excessive static deflection observed in the springs of conventional translational vibrating systems can be minimized in the proposed device. A prototype was built and tested on the harmonic motion generator. The maximum normalized RMS power was measured to be 3.6 Ws4/m2 at 0.45 Hz ; its 3 dB bandwidth was 0.30 Hz, which amounts to a period of 1.4 s.
Keywords:
Energy Harvesting, Wave Energy Converter, Yo-yo Vibrating System, Static Deflection, Low Frequency키워드:
에너지 수확, 파력발전장치, 요요 진동 시스템, 정적 처짐, 저주파1. 서 론
파력은 해양에너지 중 하나로 바다 표면에 존재하는 파동에너지를 의미하며 파력발전은 이를 전력으로 변환하는 기술이다. 파력발전이 상용화될 경우 연간 2000 TWh(tera watt-hour)의 전력공급이 가능하다고 평가되고 있으며 자원이 풍부한 영국 등 북유럽에서 활발하게 연구되고 있다(1). 파력발전장치는 크게 진동수주(oscillating water column), 월파(over-topping), 가동물체(oscillating body) 형으로 분류되며 이중 가동물체 파력발전 장치는 수면의 움직임에 따라 민감하게 반응하는 부이(buoy)의 움직임을 전기에너지로 변환하는 기술로서 파력에너지를 직접 이용하므로 에너지 효율이 높은 반면 구조적 안정성이 취약한 특징을 갖고 있다.
가동물체형 파력발전 장치는 부이와 해저면, 고정된 구조물, 또는 다른 부이와의 상대운동으로부터 전력을 생산한다. 부이의 운동은 파도의 크기 및 주기에 따라 변화하게 되는데, 일반적으로 부이의 질량와 부력의 형태로 나타나는 탄성에 의해 결정되는 공진주기와 파도의 주기가 일치할 때 가장 큰 운동이 나타나게 된다(2). 이러한 부이의 특성을 이용하여 발전효율을 높이기 위한 다양한 연구가 이루어져 왔다. Budar and Falnes(3)는 부이와 해저면을 연결하는 계류선(mooring wire)를 감는 플라이휠의 관성모멘트를 조절하여 부이의 공진주기를 변경하는 아이디어를 제시하였고 Li 등(4)은 가변관성 플라이휠(variable inertia flywheel) 장치를 제안하여 이를 구체화하였다. 또한 파도의 운동에 맞추어 계류선의 장력을 조절하거나(5) 잠금(latching)과 단속(de-clutching)을 적절하게 하여 부이의 운동을 증폭시키는 기법(6), 또는 내부 발전기의 댐핑력을 조절하여 발전효율을 높이는(7) 등의 방법 들이 제시되었다. 이러한 능동 또는 반능동 제어 방법은 파도의 변화에 효율적으로 적응할 수 있는 장점이 있는 반면 지속적인 제어가 필요하다. 최근 음의 강성을 구현하는 쌍안정 비선형 스프링을 사용하여 출력 및 발전 주파수 대역을 향상시킬 수 있는 수동제어 방식의 파력발전장치가 제안(8)되었으며 Younesian and Alam(9)은 3중 안정 시스템을 도입하여 발전대역을 보다 확장하였다. 이러한 능동 또는 수동형 가동물체형 파력발전 장치들은 모두 파도 및 부이의 운동으로 인해 계류선에 인가되는 장력을 이용하여 해저면 또는 부이에 설치된 발전기를 이용하여 전력을 생산한다.
이 연구에서 다루고자 하는 부이 내부에 내장된 공진형 파력발전장치는 파도 가진에 의해 발생하는 무게추의 관성력을 이용하여 발전을 하게 되므로 외부환경으로부터 발전장치가 완전히 분리되어 해수에 의한 부식 및 작동부에 해양생물이 부착되므로 발생할 수 있는 고장 등의 문제가 존재하지 않는 장점이 있다. Nabavi 등(10)과 Viet and Wang(11)은 파도의 흔들림(pitching) 가진으로부터 전력을 생산하는 부이 내장 공진형 파력발전장치를 제안하였다. 파도의 상하요동(heaving)을 이용하는 부이 내장 공진형 파력발전장치에 관해서는 Cho and Kweon(12), Choi 등(13), Han and Lee(14) 등이 개념제시 및 수치적 연구를 수행하였다.
일반적으로 파도 가진주파수는 0.1 Hz ~ 1 Hz 의 저주파 범위에서 나타나게 되므로 내장 공진형 진동시스템을 여기에 동조시킬 경우 무게추의 질량에 비해 상대적으로 작은 강성 값을 얻게 된다. 흔들림 방식의 내장 공진형 파력발전 장치의 경우 무게추가 수평운동을 하므로 이것이 큰 문제가 되지 않으나 상하요동 방식의 경우 파력발전장치의 출력을 높이기 위해 무게추의 질량을 높이게 되면 결과적으로 매우 큰 정적 처짐(static deflection)이 발생하게 되어 파력발전장치를 실제로 구현하려고 할 때 스프링의 내구성 및 장치의 크기 문제가 발생한다.
이 연구에서는 무게추의 직선운동을 얼레(reel)를 사용하여 회전운동으로 변환하여 전력을 생산하는 요요 에너지 하베스터(15~19)를 파력발전에 적용하여 상하요동을 위한 부이 내장형 파력발전 장치의 정적 처짐 문제에 대한 대안을 제시하고 수치해석 및 실험을 통해 장치의 성능을 검증하고자 한다.
2. 요요 에너지 하베스터
2.1 시스템 모델링
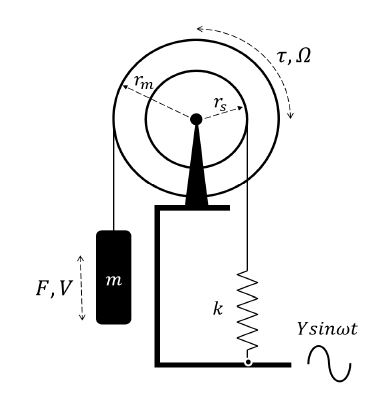
이 연구에서 다루고자 하는 요요 에너지 하베스터는 Fig. 1의 요요 진동시스템을 이용하여 전력을 생산한다. 요요 진동시스템은 동축상에 설치된 두 개의 얼레에 각각 무게추와 스프링을 와이어로 연결하고 무게추 및 스프링의 수직 변위를 얼레에 감아 회전변위로 변환하도록 고안되어 있다. 두 얼레의 반경은 각각 rm과 rs로 주어져 있으며 이로 인해 무게추와 스프링의 변위는 서로 다르게 나타나게 된다. 스프링의 강성계수를 k, 무게추의 무게를 m이라고 할 때, 직선운동을 하는 부분과 회전운동을 하는 부분의 임피던스(impedance)는 각각 다음과 같이 나타낼 수 있다.
| (1a) |
| (1b) |
여기서, F와 V는 각각 무게추에 작용하는 가진력과 무게추의 속도이며 τ와 Ω는 회전축의 토크와 각속도이다. c는 기계 및 전기적 감쇠상수이며 J는 무게추 부분을 제외한 회전부의 관성모멘트를 의미한다. ω는 파도의 각진동수를 나타낸다. 회전부와 직선부의 임피던스 사이에는 의 관계가 존재하므로 이를 이용하면 식 (1)을 다음과 같이 변환할 수 있다(15).
| (2) |
파도의 진폭이 Y 일 때, 이로 인해 무게추에서 발생하는 관성토크는 τ=-mrmYω2sinωt라 할 수 있다. 이를 식 (2)에 대입하면 얼레의 회전각속도의 크기를 식 (3)과 같이 얻을 수 있다.
| (3) |
식 (3)의 분모로부터 요요 진동시스템이 가장 큰응답을 나타내게 되는 비감쇠 공진주파수(f) 및 공진 주기(T)를 얻을 수 있다.
| (4) |
여기서, 이다. 식 (4)에서 볼 수 있듯이 요요 진동 시스템의 공진주파수는 시스템의 무게를 증가시키거나 강성계수를 낮추는 등 기본적인 물리량을 변화시키지 않고 기하적 파라메터인 nr 값을 변화시키는 것으로 조절할 수 있다.
2.2 특성
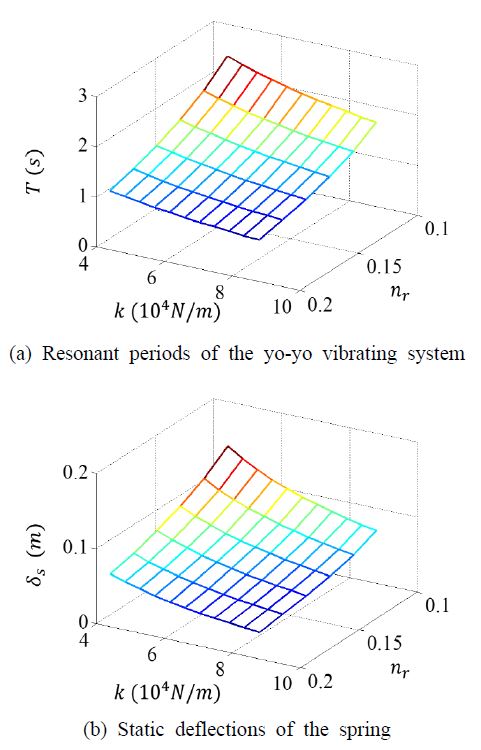
요요 진동 시스템의 특성을 알아보기 위해 Table 1의 파라메터를 적용하여 해석을 수행하였다. 무게추의 무게 및 무게추 얼레의 반경을 일정하게 유지한 상태에서 강성계수와 스프링 얼레의 반경을 각각 200 % 까지 증가시키며 시스템의 공진주기를 식 (4)를 이용하여 계산하였고 그 결과를 Fig. 2(a)에 나타내었다. 최대 공진주기(주파수)는 nr = 0.1, k = 44 × 103 N/m 일 때 2.38초(0.42 Hz)로 나타났다. 식 (4)에서 알 수 있듯이 공진주기는 얼레의 비율 nr와 강성계수의 제곱근에 각각 반비례한다. 따라서, 공진주기를 높이기 위해서는 강성계수보다 얼레의 반경비(nr)을 감소시키는 것이 보다 효율적인 것을 알 수 있다. Fig. 2(b)는 스프링의 정적변위를 다음 식을 이용하여 구한 후 동일한 조건에서 나타내었다.
| (5) |
Fig. 2(b)에서 스프링의 최대 정적 처짐은 140 mm로 나타나는 것을 알 수 있다. 강성과 반경비가 정적 변위에 미치는 영향은 식 (5)에서 알 수 있듯이 동일하다.
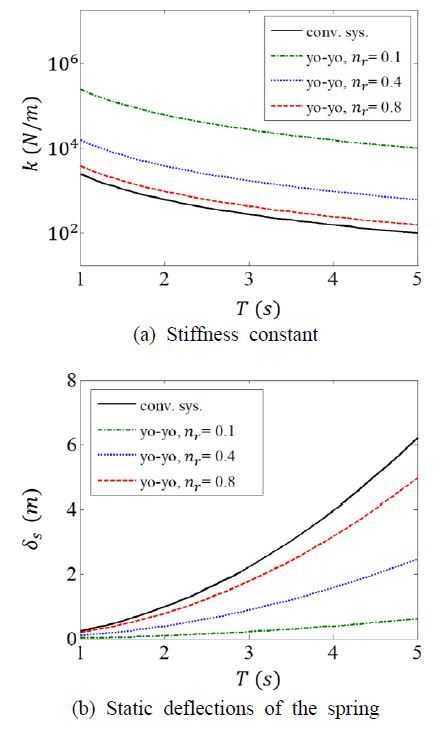
서론에서 기술한 바와 같이 진동시스템이 파도와 같은 저주파 진동환경에 동조될 경우, 스프링의 과도한 정적처짐이 발생할 수 있다. 요요진동시스템과 스프링과 질량이 직렬로 연결된 기존의 병진 진동시스템의 정적 처짐의 크기를 비교하기 위해서 무게추 질량을 고정한 상태에서 시스템의 공진주기(주파수)를 1초(1 Hz)부터 5초(0.2 Hz)까지 증가(감소)시킬 경우 요구되는 강성계수와 이때 스프링에 발생하는 정적처짐을 식 (4)와 식 (5)를 이용하여 계산하여 Fig. 3에 나타내었다. 검은 실선은 기존의 병진 진동시스템을 의미한다. 시스템의 공진주기가 길어질수록 강성계수가 급속히 감소하는 것을 볼 수 있으며 정적처짐은 이와 반대로 증가하는 것을 볼 수 있다. 이렇게 정적처짐이 크게 발생할 경우 장치의 크기가 증가할 뿐만 아니라 스프링의 과도한 변형으로 인한 내구성 문제가 발생하게 된다. 반면, 요요 진동시스템의 경우 Fig. 3에서 볼 수 있듯이 동일한 공진주기를 위해 요구되는 강성계수의 크기가 상대적으로 크게 나타나며 정적처짐의 크기는 작게 나타나게 되는데 nr값이 작을수록 정적처짐이 줄어들게 된다. 반경비가 0.1인 경우 기존시스템에 비해 강성계수는 100배 증가하고, 정적처짐은 0.1배로 줄어드는 것을 확인할 수 있다.
2.3 시작품 구성
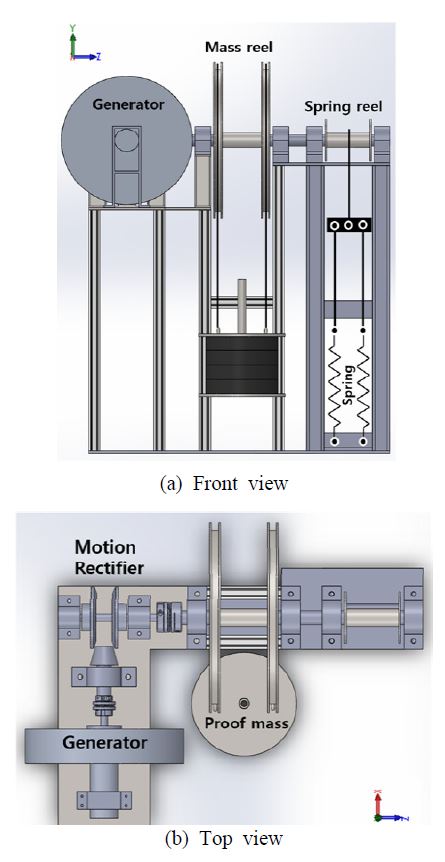
Fig. 4는 요요진동시스템에 회전 발전기를 결합한 시작품의 형태를 나타내고 있다. 무게추는 얼레에 감긴 2개의 와이어에 의해 매달려 있으며 마찬가지로 2개의 스프링이 스프링얼레에 감긴 와이어에 의해 당겨지고 있다. 무게추 얼레와 스프링 얼레는 축에 고정되어 함께 회전하며 반경비는 0.1이다. 지반가진으로 인해 무게추가 반복병진운동을 할 때, 축은 반복 회전운동을 하게 되는데 Fig. 4(b)에서 볼 수 있듯이 이는 베벨기어와 원웨이베어링을 이용하여 구성한 기계적 모션정류장치에 의해 단방향 회전운동으로 변환되어 발전기에 전달되어 전력을 생산하도록 구성하였다. 발전기의 회전 속도를 증가시키기 위해 모션정류장치의 기어비 N을 도입하였을 때 발전기의 출력 전압은 식 (6)과 같이 얻을 수 있다.
| (6) |
여기서 CV는 기전력과 회전속도 사이의 관계를 나타내는 발전기 속도상수이다.
2.4 실험 및 결과
요요 파력발전장치의 성능을 확인하기 위하여 가진실험을 수행하였다. Fig. 5(a)는 가진시험을 위해 제작된 파력발전장치 시작품의 전체 구성을 보여주고 있다. 질량과 스프링이 각각 무게추 얼레와 스프링 얼레에 매달려 있으며 각 얼레는 하나의 회전축에 의해 연결되어 있다. 회전축의 왕복 회전운동은 모션정류 장치를 거쳐 한방향의 회전운동으로 변환되어 AFPM(axial flux permanent magnet) 방식의 발전기에 전달되도록 구성하였다. 가진실험은 Fig. 5(b)의 조화운동발생장치(motion generator)를 제작하여 수행하였다. 조화운동발생장치는 모터의 회전운동을 병진운동으로 변환, 상부에 설치된 와이어에 매달린 시작품을 가진할 수 있도록 설계되었다. Fig. 5(c)는 측정장치를 보여주고 있다. 전압, 전류 및 전력은 발전기와 20 Ω의 부하저항을 파워메터(Yokogawa WT330)에 연결하여 측정하였으며 회전축의 각변위는 엔코더(오토닉스 E50S8-100-3-T-1)와 National Instrument사의 PXI 시스템을 이용하여 기록하였다.
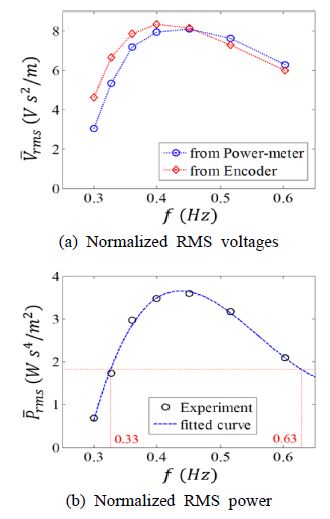
Fig. 6은 실험을 통해서 계측된 결과를 나타내고 있다. Fig. 6(a)는 파워메터에서 계측된 결과와 엔코더에서 얻어진 각변위를 속도로 변환한 후 이를 식 (6)을 이용하여 계산한 결과를 비교한 것이다. 계측결과는 모두 실효(root mean square)값으로 변환하여 나타내었으며 입력의 영향을 보상하기 위해 입력가속도로 나누어 정규화하였다. 최대 전압은 0.4 Hz에서 나타났으며 이는 주기 2.5초에 해당한다. 이는 수치적 연구에서 얻어진 공진주기 2.38초와 거의 일치한다. 발전기의 전압출력은 저주파 부분에서는 회전속도로부터 계산된 값보다 작으나 고주파에서는 더 큰 것을 확인할 수 있는데, 이는 속도에 따른 발전기의 효율변화에 의한 것으로 보인다.
Fig. 6(b)는 파워메터에서 얻어진 실효 전력값을 입력가속도의 제곱으로 정규화한 결과를 나타내고 있다. 최대 정규 실효전력은 0.45 Hz(주기 2.22초)에서 3.6 Ws4/m2로 나타나는 것을 볼 수 있다. 바다환경에서 파도의 주기는 시간에 따라 변동하게 되므로 파력발전장치 출력의 주파수 대역은 넓을수록 유리하다. 최고 전력 출력의 3 dB 이내에 해당하는 대역은 0.33 Hz에서 0.63 Hz로 나타나는데, 주기로는 1.6초에서 3.0초 사이에 해당한다. 즉 제안한 요요파력발전 장치의 발전 주기(주파수)대역은 1.4초(0.3 Hz)이다.
3. 결 론
이 논문에서는 파도의 상하요동에 의해 작동하며 부이 내부에 설치가 가능한 공진형 파력발전장치를 다루었다. 파도의 낮은 가진 주파수에 적용할 수 있는 요요 진동시스템을 이용한 파력발전장치를 제안하였고 육상 가진실험 결과를 제시하였다. 수치 예를 통해 공진주파수가 낮을 경우 요요진동시스템이 기존 병진 진동시스템에 비해 정적처짐이 작게 나타나는 것을 보였다. 가진실험에서 63 kg의 무게추를 적용하였을 때, 0.45 Hz에서 3.6 Ws4/m2의 정규화된 RMS 최대 출력을 얻었으며 주기대역은 1.4초로 나타나는 것을 확인하였다. 요요 파력발전 장치는 기존의 병진형 진동시스템을 이용한 파력발전 장치가 바다의 매우 낮은 저주파 가진 환경에서 나타내는 단점들을 보완할 수 있다고 판단되며 향후 추가 연구를 통해 실용성을 높여나가고자 한다.
Acknowledgments
이 논문은 2019년도 호서대학교의 재원으로 학술연구비 지원을 받아 수행된 연구임(2019-0842).
References
- Jung, D. H., 2012, Wave Power Generation – Market Perspectives and Strategies, KISTI Market Report, pp. 20~23.
-
Falnes, J., 2002, Ocean Waves and Oscillating Systems, Cambridge University Press, UK.
[https://doi.org/10.1017/CBO9780511754630]

-
Budar, K. and Falnes, J., 1975, A Resonant Point Absorber of Ocean-Wave Power, Nature. Vol. 256. pp. 478~479.
[https://doi.org/10.1038/256478a0]

-
Li, Q., Li, X., Mi J., Jiang, B., Chen, S. and Zuo, L., 2020, Tuable Wave Energy Converter Using Variable Inertia Flywheel, IEEE Transactions on Sustainable Energy, Vol. 12, No. 2, pp. 1265~1274.
[https://doi.org/10.1109/TSTE.2020.3041664]

- Li, B., Crozier, R. and Macpherson, E., 2011, Reactive Causal Control of a Linear Generator in Irregular Waves for Wave for Wave Power System, Proceeding of 9th European Wave and Tidal Energy Conference (EWTEC 2011), Southampton, UK.
-
Clément, A. H. and Babarit, A., 2012, Discrete Control of Resonant Wave Energy Devices, Philosophical Transactions of the Royal Society A, Vol. 370, No. 1959, pp. 288~314.
[https://doi.org/10.1098/rsta.2011.0132]

-
Vantorre, M., Banasiak, R. and Verhoeven, R., 2004, Modelling of Hydraulic Performance and Wave Energy Extraction by a Point Absorber in Heave, Applied Ocean Research, Vol. 26, No. 1-2, pp. 61~72.
[https://doi.org/10.1016/j.apor.2004.08.002]

-
Todalshaug, J. H., Ásgeirsson, G. S., Hjálmarsson, E., Maillet, J., Möller, P., Pires, P., Guérinel. M. and Lopes, M., 2016, Tank Testing of an Inherently Phase-Controlled Wave Energy Converter, International Journal of Marine Energy, Vol. 15, pp. 68~84.
[https://doi.org/10.1016/j.ijome.2016.04.007]

-
Younesian, D. and Alam, M. R., 2017, Multi-Stable Mechanism for High-Efficiency and Broadband Ocean Wave Energy Harvesting, Applied Energy, Vol. 197, pp. 292~302.
[https://doi.org/10.1016/j.apenergy.2017.04.019]

-
Nabavi, S. F., Farshidianfar, A. and Afsharfard, A., 2018, Novel Piezoelectric-Based Ocean Wave Energy Harvesting from Offshore Buoys, Applied Ocean Research, Vol. 76, pp. 174~183.
[https://doi.org/10.1016/j.apor.2018.05.005]

-
Viet, N. V. and Wang, Q., 2018, Ocean Wave Energy Pitching Harvester with a Frequency Tuning Capability, Energy, Vol. 162, pp. 603~617.
[https://doi.org/10.1016/j.energy.2018.08.067]

-
Choi, I.-H. and Kweon, H.-M., 2011, Extraction of Wave Energy Using the Coupled Heaving Motion of a Circular Cylinder and Linear Electric Generator, Journal of Ocean Engineering and Technology, Vol. 25, No. 6, pp. 9~16.
[https://doi.org/10.5574/KSOE.2011.25.6.009]

-
Choi, Y. H., Lee, C. J. and Hong D. S., 2012, Dynamic Design of a Mass-Spring Type Translational Wave Energy Converter, Korean Society of Manufacturing Technology Engineers, Vol. 21, No. 1, pp. 182~189.
[https://doi.org/10.7735/ksmte.2012.21.1.182]

-
Han, K. B. and Lee, H. W., 2013, The Research of Wide Band Vibration Energy Harvester Using Ocean Wave, Journal of the Korean Society of Marine Engineering, Vol. 37, No. 6, pp. 596~602.
[https://doi.org/10.5916/jkosme.2013.37.6.596]

-
Jang, S. J., Kim, I. H., Jung, H. J. and Lee, Y. P., 2011, A Tunable Rotational Energy Harvester for Low Frequency Vibration, Applied Physics Letters, Vol. 99, No. 13, 134102.
[https://doi.org/10.1063/1.3644130]

-
Jang, S. J., Kim, I. H., Park, K. and Jung, H. J., 2016, An Enhanced Tunable Rotational Energy Harvester with Variable Stiffness System for Low-frequency Vibration, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 230, No. 5, pp. 732~736.
[https://doi.org/10.1177/0954406215587727]

-
Kim, I.-H., Jang, S.-J., Park, S.-H., Jung, H.-J. and Kim, Y.-C., 2020, Tunable Yo-Yo Energy Harvester with Oblique Springs, Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science. Vol. 234, No. 16, pp. 3185~3194.
[https://doi.org/10.1177/0954406220913593]

-
Sim, K., Park, J. and Jang, S.-J., 2015, Electro-Mechanical Modeling and Performance Analysis of Floating Wave Energy Converters Utilizing Yo-Yo Vibrating System, Transactions of the Korean Society of Mechanical Engineers A, Vol. 39, No. 1, pp. 79~87.
[https://doi.org/10.3795/KSME-A.2015.39.1.079]

-
Jang, S.-J., Kwon, J.-T. and Kim, Y.-C., 2017, Performance Evaluation of an Oscillating Body Wave Energy Converter Utilizing Multi-stage Stiffness System, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 7, pp. 886~892.
[https://doi.org/10.5050/KSNVE.2017.27.7.886]


Seon-Jun Jang received a B.S., M.S. and Ph.D degree in Dept. of Mechanical Engineering of Yonsei University in 1999, 2001, and 2007, respectively. He is currently working as an associate professor at Hoseo University. His researches are mainly focused on the design of vibrational energy harvesters using multi coupled degree of freedom vibrating systems and wave energy converters.

Byeong-Ryong Kim is a Ph.D. candidate in the graduate school of mechanical engineering at Hoseo University. His research interests are energy harvesting, wave energy conversion, and artificial intelligent.