블레이드와 로터의 결합 조건에 의한 Mistuning 효과
© The Korean Society for Noise and Vibration Engineering
Abstract
In this study, the assembling conditions of blades and rotors are investigated by the FEM model of a blade with the different boundary conditions. It is assumed that the modal properties of blades are identical and the blade modal frequencies are changed by the assembling condition only. It is shown that the change in modal frequency by the assembling condition is approximately 0.25 % in normal operating conditions. However, the variance of blade response can be increased by more than 30 % under narrow-band random excitations.
Keywords:
Mistuning, Bladed Disk Assembly, Fir-tree Type Blade Root, Blade Boundary Condition, Narrow Band Random Excitation, Response Variance키워드:
미스튜닝, 블레이드 시스템, 전나무 형상 블레이드 하단부, 블레이드 경계조건, 좁은 주파수 밴드의 랜덤 가진력, 응답의 분산값1. 서 론
가스터빈의 각 단의 블레이드는 동일한 형상으로 제작되어 동일한 작동 상태에 있음에도 일부 블레이드의 진동이 심하게 진행되는데 이는 mistuning 효과라고 알려져 있다. 각 블레이드는 제작 공차로 인하여 모달 특성이 미세하게 차이가 나는데, 이로 인한 진동은 큰 폭으로 차이가 나서 피로 파손의 원인으로 파악되고 있다(1~3).
이러한 mistuning 효과를 해석하기 위하여 사용하는 모델링은 블레이드의 강성 행렬에 작은 크기의 변수를 포함하는 것이 일반적이다(4~6). 집중 질량의 단순한 모델에서(4,5) 유한요소 모델에 기반한 복잡한 모델까지 다양하게 사용되고 있는데(6), 최근에는 블레이드의 모달특성외에 형상의 차이에 의한 영향까지 고려하여 블레이드의 질량행렬에도 변수를 포함하여 해석하는 경우도 있다(7,8). 개별 블레이드의 유한요소법을 이용한 모달 해석에서는 블레이드의 상부 구조만 해석하거나(9), 블레이드의 하부와 로터를 접촉조건이나 커플링구조를 이용하여 동시에 해석하는 방법을 사용하였다(10,11). 블레이드의 하부는 작동과정에서 열팽창에 의하여 로터와 결합하는데, 이러한 결합 상태의 차이가 mistuning 효과에 미치는 영향에 대하여는 별다른 연구가 진행된 바가 없다.
이 논문에서는 블레이드의 개별적인 모달 특성은 동일하다고 가정하고, 로터와의 결합 조건에 의한 mistuning의 영향만을 분석하였다. 일반적으로 터빈 시스템에서는 동일한 주파수와 일정한 위상을 가지는 engine-order-excitation을 외력으로 사용하는 경우가 일반적이지만, 많은 경우에 터빈 시스템에 작용하는 외력은 비주기적인 특성을 가진다고 밝혀지고 있다(12). 그리고 주파수 대역이 넓은 white noise인 경우에는 mistuning 효과가 작다는 것이 알려져 있으므로(5) 좁은 주파수 대역을 가지는 비주기적인 힘을 블레이드에 작용하는 외력으로 가정하였다. 먼저 블레이드의 경계 조건에 의한 모달 해석의 차이를 살펴보고 이러한 차이에 의하여 발생하는 시스템의 응답을 분석하였다.
2. 블레이드의 모달 해석
2.1 블레이드의 모델링
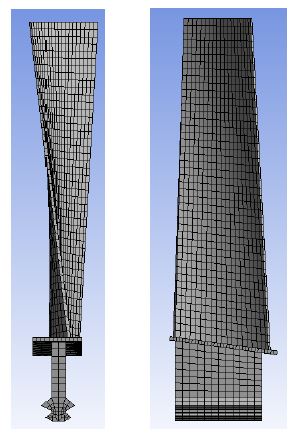
터빈 블레이드와 디스크의 결합은 dovetail 형태 또는 fir-tree 형태의 블레이드 하단의 형상을 사용한다. 일반적으로 fir-tree 형식이 많이 사용되고 있는데, 그 이유는 접촉면적을 넓게 하여 fretting 피로에 내구 수명을 길게 설계할 수 있기 때 문이다. 이러한 블레이드의 결합부는 축과 밀착되어 터빈 엔진의 작동 중에 발생하는 원심력과 열팽창, 고압가스로 인한 휨과 비틀림의 하중을 받는다. 이때 각각의 블레이드는 조립 공차와 결합 조건의 미세한 차이로 인하여 각각의 블레이드의 진동 특성도 달라진다고 할 수 있다. 이러한 진동 특성을 검토하기 위하여 fir-tree 형식의 GE J-85-CJ-610 엔진의 블레이드를 3차원 측정하여 확보한 3D 모델을 바탕으로 형상을 단순화하여 Fig. 1과 같은 유한요소모델을 생성하였다.
이 모델은 ANSYS-workbench의 multi-zone방법을 이용하여 육면체 요소를 기본으로 메쉬를 생성하였다. 메쉬 생성에 사용한 상세한 조건은 Table 1에 나타나 있고, 해석에 사용한 물성치는 Table 2에 나타나 있다.
2.2 블레이드의 경계조건
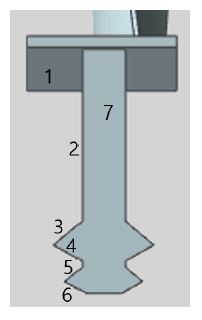
터빈 엔진의 작동 과정에서 블레이드의 fir-tree 결합부에서는 micro-slip이 발생하는데, 이러한 비선형의 실제 작동 조건을 선형진동해석에서 적용할 수 있는 경계조건으로 변환하는 것은 쉽지 않다. 왜냐하면 선형 해석의 경계 조건은 힘과 위치의 정보로 표현되어야 하는데 stick-slip이 발생하는 실제 조건을 힘과 위치로 정의하는 것은 어렵기 때문이다(11). 이러한 마찰 현상을 해석하는 일반적인 방법은 블레이드가 축에 고정되어 있다고 가정하고 별도의 마찰 댐퍼를 추가하는 방법이 사용된다(13). 이러한 비선형 해석없이 블레이드의 모달 특성을 분석하기 위하여 경계조건에서 결합 표면이 고정되는 상황과 결합 표면의 수직방향으로 움직임이 제한되는 상황을 예상하였다. 그리고 경계 조건의 차이에 의한 블레이드 동특성의 변동을 분석하기 위하여 결합부 표면을 Fig. 2와 같이 7개로 분리하였다.
우측의 표면은 좌측의 표면과 동일한 결합조건으로 가정하였다. 그리고 분리된 표면에 고정 조건과 수직방향의 구속 조건, 그리고 구속이 전혀 없는 자유 조건의 3가지 조건을 혼합하여 Table 3과 같이 6가지의 상황에 대하여 진동해석을 수행하였다. 여기서 ‘F’는 모든 방향에 대한 고정 조건을 나타내고, ‘C’는 표면의 수직 방향에 대한 구속 조건, 그리고 ‘-‘는 자유조건으로 구속이 없는 상태를 나타낸다.
2.3 블레이드의 모달 해석
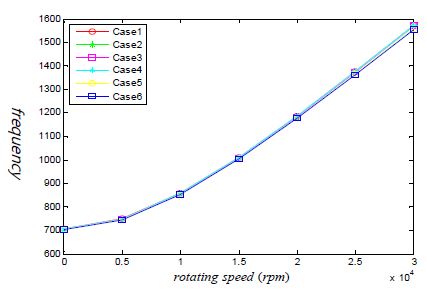
터빈의 회전 속도의 증가에 따라 블레이드의 제1 고유진동수를 해석한 결과는 Fig. 3에 나타나 있다. 회전의 중심축은 블레이드의 결합부 하단에서 345 mm에 위치한 것으로 설정하였다. 원심력에 의한 stress stiffening 효과로 인하여, 회전속도가 증가하면 블레이드의 고유진동수가 점점 증가하고 있으며, 경계 조건의 차이에 의한 영향도 점점 증가하고 있다. 즉 완벽하게 동일한 동특성을 가진 터빈 블레이드라고 하더라도, 결합 상태에 따라 각 블레이드의 고유진동수는 편차를 가질 수 있으며 이러한 결과는 Table 4에 정리되어 있다. 선정된 6가지의 경계 조건 이외에 다른 경계조건을 검토하여도 Table 4의 결과는 크게 변화하지 않았다.
3. 터빈 블레이드 시스템의 진동
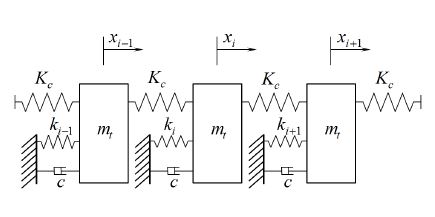
결합 상태에 따른 각각의 블레이드의 고유 진동수의 변동이 작동 상황에서 블레이드의 진폭에 미치는 영향을 알아보고자 Fig. 4와 같은 단순한 터빈 시스템의 모델을 사용하여 시스템의 응답을 수치적으로 계산하였다. 블레이드의 개수는 24개로 선정하였고 각 블레이드의 강성의 변동으로 고유진동수의 변동을 표현하였다. 그 외의 블레이드 질량과 댐핑 계수, 디스크의 영향에 의한 연결 강성은 일정하다고 가정하였다. 수치 해석에 사용된 시스템 계수는 Table 5에 정리되어 있다(4,5,13).
블레이드의 강성 변동에 의한 고유진동수의 표준 편차는 0.25 %로 설정하였고, 이 변동량은 작동 속도에 일정하다고 가정하였다. 터빈 시스템에 작용하는 외력은 댐핑비가 1 %인 band-pass filter를 사용하여 입력을 white noise로 하여 생성되는 narrow-band random excitation으로 설정하였다. 시스템의 운동 방정식을 간단하게 살펴보면 식 (1) ~ (2)와 같다.
| (1) |
| (2) |
여기서 M, C와 K는 블레이드 시스템의 질량, 댐핑 및 강성 행렬이다. 필터에서는 외력의 bandwidth를 결정하고 ωF는 외력의 주요주파수를 결정한다.
그리고 필터의 연결구조를 결정하는 CR에 의하여 외력의 correlation이 결정된다(5). 위의 운동방정식은 적절한 상태 변수를 선택하여 다음의 일차미분방정식으로 표현할 수 있다.
| (3) |
외력에 대한 블레이드의 응답은 진폭의 분산값으로 정의되고, 다음의 Lyapunov 방정식에서 구해진다(4,5).
| (4) |
식 (4)에서 각 행렬은 아래와 같다.
| (5) |
| (6) |
| (7) |
| (8) |
| (9) |
Q0는 white noise의 강도로 시스템의 응답에 단순한 비례값의 역할을 하므로 단위 값을 사용하였다. 각 블레이드 stiffness의 표준편차가 2150 N/m인 블레이드 시스템을 정규분포를 가지도록 천개를 생성하여 외력의 변화에 따른 블레이드의 응답 변화를 계산하였다.
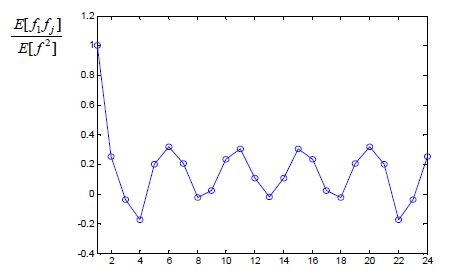
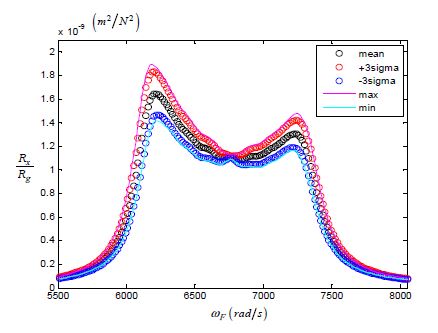
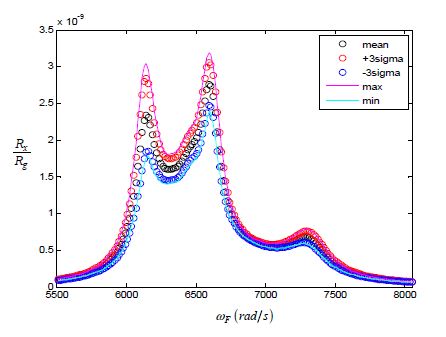
외력은 correlation 특성에 따라 서로 관련성이 없는 경우와 Fig. 5와 같은 correlation을 가지는 2가지 경우를 대상으로 하였다. 외력의 일정한 강도에서 블레이드 진폭의 분산값을 구하여 평균, 최대 및 최소값과 3시그마값을 Fig. 6과 Fig. 7에 나타내었다. Figs. 6, 7의 좌표축에 표시된 Rx와 Rg는 블레이드의 진폭과 외력의 분산값으로 식 (10)과 같이 표현된다.
| (10) |
| (11) |
Fig. 6에 표현된 것과 같이 외력이 서로 관련되지 않은 상태에서는 블레이드의 분산의 평균값은 공진 현상이 발생하는 주파수 대역의 6145 rad/s에서 큰 진폭을 나타내고 7225 rad/s에서는 상대적으로 작은 진폭을 보여주고 있다. 그리고 공진대역에서 최대 진폭은 최소 진폭과 비교하여 51 %의 증가를 보여준다. 외력이 correlation을 가지는 경우에는 Fig. 7과 같이 공진 대역의 6145 rad/s와 6595 rad/s에서 두개의 높은 피크 값을 보여주고 7060 rad/s 이후의 진폭은 비교적 낮아서 실질적으로 공진 대역이 좁아진 것과 같은 현상을 나타낸다. 그리고 좁아진 공진 대역을 기준으로 하여도 최대 진폭은 최소 진폭과 비교하여 73 %의 증가를 보여준다.
블레이드의 진폭의 분산값은 평균에 비하여 외력의 correlation이 없는 경우에는 최대 31 % 증가하고 correlation이 있는 경우에는 최대 38 % 증가하였다. 즉 결합 상태에서 발생하는 고유진동수의 변화가 약 0.25 %일 때 이에 따른 블레이드의 진폭은 30 %이상 증가할 수 있다는 것을 알 수 있다.
4. 결 론
터빈 블레이드의 mistuning의 원인에 대하여 각 블레이드의 모달 특성의 편차에 대하여는 많은 연구가 이루어졌으나 블레이드 결합 조건의 영향에 대하여는 별다른 연구가 이루어지지 않은 상태였다. 이 연구에서는 블레이드의 fir-tree 부분을 7구역으로 나누어서 축과의 결합 조건을 고정, 구속 및 자유조건으로 구분하여 적용한 결과 일반적인 15 000 r/min의 작동조건에서 약 0.25 %의 모달 주파수의 표준 편차를 발생시킬 수 있는 것을 확인하였다. 블레이드 시스템의 단순한 모델을 이용하여 블레이드의 결합 조건의 차이로 인하여 작동상태에서는 블레이드의 진폭은 30 %이상 증가할 수 있다는 것을 발견하였다. 블레이드의 진동은 외력의 correlation에 민감하게 반응하여, 공진 조건과 mistuning 영향이 변화하므로 이러한 영향을 충분히 고려하여 블레이드 시스템이 설계되어야 한다는 것을 알 수 있었다. 향후의 연구에서 블레이드의 작동상태에서의 micro-slip에 의한 영향을 고려하고 외력의 correlation에 대한 자료를 확보한다면 더욱 정확한 해석 결과를 얻을 수 있을 것으로 판단된다.
Acknowledgments
이 논문은 2020년도 한국기술교육대학교 교수 교육연구진흥과제 지원에 의하여 연구되었음.
References
-
Sogliero, G. and Srinivasan, A. V., 1980, Fatigue Life Estimates of Mistuned Blades Via a Stochastic Approach, AIAA Journal, Vol. 18, No. 3, pp. 318~323.
[https://doi.org/10.2514/3.7654]

-
Griffin, J. H. and Hoosac, T. M., 1984, Model Development and Statistical Investigation of Turbine Blade Mistuning, ASME Journal of Vibration, Acoustics, Stress, and Reliability in Design, Vol. 106, No. 2, pp. 204~210.
[https://doi.org/10.1115/1.3269170]

-
Sinha, A., 1986, Calculating the Statistics of Forced Response of a Mistuned Bladed Disk Assembly, AIAA Journal, Vol. 24, No. 11, pp. 1797~1801.
[https://doi.org/10.2514/3.9526]

-
Cha, D. and Sinha, A., 2002, Effects of the Nature of Excitation on the Response of a Mistuned Bladed Disk Assembly, ASME Journal of Turbomachinery, Vol. 124, No. 4, pp. 588~596.
[https://doi.org/10.1115/1.1508385]

-
Cha, D., 2017, Effects of Correlations of Narrow Band Random Excitations on the Response of a Mistuned Bladed Disk Assembly, International Journal of Precision Engineering and Manufacturing, Vol. 18, No. 6, pp. 853~862.
[https://doi.org/10.1007/s12541-017-0101-9]

-
Lim, S.-H., Bladh, R., Castanier, M. P. and Pierre, C., 2007, Compact, Generalized Component Mode Mistuning Representation for Modeling Bladed Disk Bibration, AIAA Journal, Vol. 45, No. 9, pp. 2285~2298.
[https://doi.org/10.2514/1.13172]

-
Sinha, A., 2009, Reduced-order Model of a Bladed Rotor with Geometric Mistuning, ASME Journal of Turbomachinery, Vol. 131, No. 3, 031007.
[https://doi.org/10.1115/1.2987237]

- Bhartiya, Y. and Sinha, A., 2013, Reduced Order Modeling of a Bladed Rotor with Geometric Mistuning via Estimated Deviations in Mass and Stiffness Matrices, ASME Journal of Engineering for Gas Turbine and Power, Vol. 135, No. 5, 052501.
-
Lee, A. S., Kim, Y. C. and Lee, D. H., 2004, Evaluation of Blades Vibration Reliabilities of KGT-74 Small Gas Turbine, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 14, No. 5, pp. 410~415.
[https://doi.org/10.5050/KSNVN.2004.14.5.410]

-
Yang, K. H. and Song, O., 2009, Variation of Dynamic Characteristics of a Low Pressure Turbine Blade with Crack Length, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 12, pp. 1281~1288.
[https://doi.org/10.5050/KSNVN.2009.19.12.1281]

-
Yang, K. H., Song, O., Cho, C. W., Yun, W. N. and Jung, N. G., 2010, Fracture Mechanism of Gas Turbine Compressor Blades in a Combined Cycle Power Plant, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 20, No. 11, pp. 1025~1032.
[https://doi.org/10.5050/KSNVE.2010.20.11.1025]

-
Choi, Y-S. and Lee, K-W., 2010, Investigation of Blade Failure in a Gas Turbine, Journal of Mechanical Science and Technology, Vol. 24, No.10, pp. 1969~1974.
[https://doi.org/10.1007/s12206-010-0614-y]

-
Cha, D., 2018, Performance of Friction Dampers in Geometric Mistuned Bladed Disk Assembly Subjected to Random Excitations, Journal of Sound and Vibration, Vol. 426, pp. 34~53.
[https://doi.org/10.1016/j.jsv.2018.04.012]


Douksoon Cha is an assistant professor of the Korea University of Technology & Education, Cheonan, Korea. He received his Ph.D. in Mechanical Engineering from Pennsylvania State University. His research interests include vibration of turbine blade, friction damper and nonlinear dynamic.