배관계 시간이력 다지점 가진 해석의 입력 방법에 관한 연구

2.1 모사 배관계 유한요소 해석

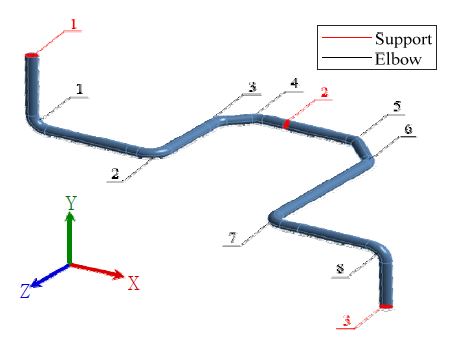
다지점 가진 시간이력 해석의 응답을 확인하기 위하여 실제 배관계와 유사한 형태의 모사 배관계를 대상으로 지진 응답 해석을 수행하였다. 상용 원전인 ARP1400의 가압기 밀림관을 모사한 배관계는 Fig. 1과 같다. 모사 대상은 8개의 곡관부를 포함한 배관계로 배관 단면의 외경은 330.2 mm, 두께는 33 mm이며 곡관부 굽힘은 495.3 mm의 곡률을 지닌다. 유한요소 해석의 모델은 Table 1과 같이 구성하였으며, 방법론에 따른 지진응답의 비교를 위하여 감쇠현상을 고려하지 않은 탄성해석을 수행하였다. 배관의 물성은 스테인리스강 재질이며 배관의 기존 밀도 7800 kg/m³에 유체에 해당하는 밀도를 인가하였다. 구체적으로 배관 내부를 차지하는 유체의 부피와 밀도를 통해 총 질량을 계산하여 구조물의 밀도에 추가하는 방식으로 배관의 밀도값을 결정하였다⁽⁸⁾.

Fig. 1

FEM diagram of NPP piping system

Table 1

Finite element model information

배관의 지지대는 높이에 따라 세 지점에 설치한 대상으로 모사하였다. 2번 지지대를 기준으로 1번과 3번 지지대의 설치 높이차는 각각 2.16 m와 2.68 m이다. 더불어 지지대가 설치되는 배관의 단면에 대한 경계조건을 설정함으로써 지지대를 모사하였으며, 지지대로 정의된 모든 단면에 대하여 완전히 구속되어 있음을 가정하였다. 구체적으로 모든 단면은 단면의 변형이 발생하지 않으며, 단면에 대하여 정의된 지지점은 모든 자유도가 구속된다. 또한 배관 구조물의 진행 중에 놓인 2번 지지대의 지진하중에 따른 거동 특성을 살펴보고자 전체 지지대를 고려한 모사 배관계와 더불어 1번, 3번 지지대만을 반영한 모사 배관계에 대해서도 지진해석을 수행하였다. 이 논문에서는 1번과 3번 지지대에 경계조건을 설정한 해석 경우를 ends supported, 그리고 모든 지지대에 대한 경계조건을 설정한 해석 경우에 대하여 all supported로 부르고자 한다.

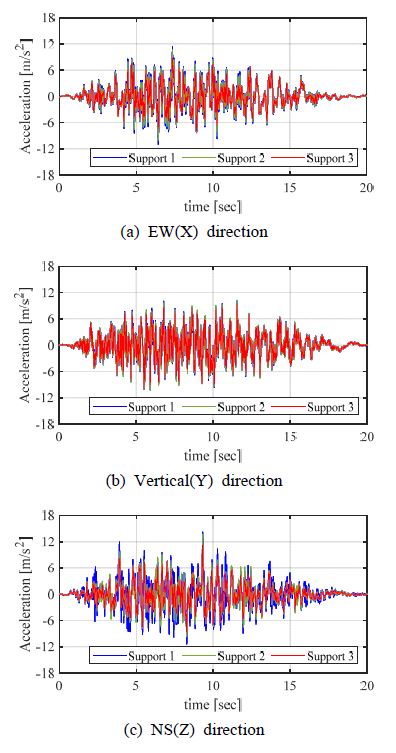
각 지지대에 대한 시간이력 가속도 데이터는 층응답 스펙트럼을 기반으로 만들어진 인공지진파이며 시간에 따른 가속도 개형은 Fig. 2와 같다. 이때 인공지진파는 모든 지지대에 대하여 동일한 위상을 갖도록 생성되었다. 또한 각 지지대에 작용하는 실제 가속도 크기에 대하여 평균 제곱근과 최대값을 Table 2에 나타냈다. 2번 지지대를 기준으로 1번과 3번 지지대에 작용한 가속도 크기의 평균 제곱근은 각각 +5.7 %와 –10.1 %에 해당하며, 인공지진파는 높이에 따라 인가되는 가속도 크기를 달리하여 생성되었다. 전체 입력의 시간은 20초이며, 관심 주파수 대역인 50 Hz까지의 성분을 파악하고자 time step은 5 ms로 설정하였다.

Fig. 2

Representative acceleration input data

Table 2

Input acceleration data on each support

지진해석은 상용 유한요소 해석 프로그램인 ANSYS 2021R1을 활용하였으며 모드중첩 시간이력해석의 경우 PCG(preconditioned conjugate gradient), 거대 질량법과 변위입력 시간이력해석의 경우 HHT(Hilbert-Huang transform) 알고리즘을 기반으로 지진해석이 수행되었다.

2.2 다지점 가진 시간이력 해석 방법론

입력 방법론에 대한 구분은 full transient 해석을 수행하는지에 대한 여부로 구분한다. 해석의 기본 단위인 절점에 대하여 모든 행렬항이 연산에 참여하는 full 시간이력해석은 transient 거동을 반영하기에 적절하지만 해석 부하가 높게 나타난다. 이와 달리 연산에 참여하는 행렬항을 줄인다면 시간이력해석이 지닌 비용적 단점을 완화할 수 있게 된다. 따라서 CMS(component mode synthesis)를 기반으로 연산행렬을 간소화할 수 있는 모드 중첩 시간이력 해석을 입력 방법으로 선정하였다⁽⁹⁾.

또한 지지점에 대하여 동일한 가속도 파라메터를 생성해내는 입력 방법론을 고려하고자 한다. 즉 지점에 대하여 직접 가속도 입력을 하지 아니하고, 하중 또는 변위값을 입력함으로써 지점에 대한 가속도를 생성하는 입력 방법론을 적용하고자 한다. 이때 하중을 입력으로 하는 입력 방법은 거대 질량법이며 지점 변위 입력 방법 또한 해당 분류에 속한다.

(3) 지점 변위 입력 시간이력 해석

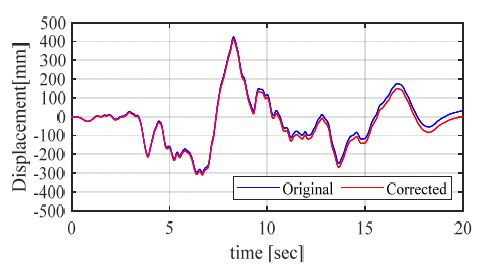
시간이력 변위를 입력으로 활용하기 위하여 가속도 데이터의 수치 적분이 요구되며, 이를 통해 기존 대표 가속도와 일치성을 지닌 가속도 개형을 생성할 수 있게 된다. 하지만 수치 적분 과정에서의 미지수인 초기 적분점의 설정에 따라 최종 시각에서 변위값이 초기 위치와 달라질 수 있다. 이러한 오차를 줄이고자 기준선 보정(baseline correction)을 수행하였으며⁽¹²⁾ Fig. 3과 같이 최종 시각에 나타나는 변위값을 보정함으로써 기존 대표 가속도와의 일치성이 드러나도록 변위 입력을 생성하였다.

Fig. 3

Generated time-history displacement input data (NS direction on support 1)

2.3 방법론에 따른 다지점 가진 유효성 및 지진해석 결과 일치성 검증

다지점 가진 조건에 부합하는지 판단하기 위하여, 방법론에 따라 층 높이에 따른 각 지지점에 대해 입력으로 활용된 가속도 값을 비교하고자 한다. 이를 위하여 각 지지대에 입력으로 활용된 시간이력 가속도 벡터의 크기에 대한 평균 제곱근 및 최대값을 Table 2에 나타내었다. 방법론에 따라 입력된 가속도는 대표 가속도 대비 최대 1.1 %의 오차를 지니며, 높이에 따라 입력된 가속도 크기의 차이를 확인할 수 있다. 다시 말해 세 방법론 모두 지지점을 입력 지점으로 하는 다지점 가진이 수행되었으며, 대표 가속도 데이터와 일치성을 지닌 유효한 지진해석이 수행되었음을 알 수 있다.

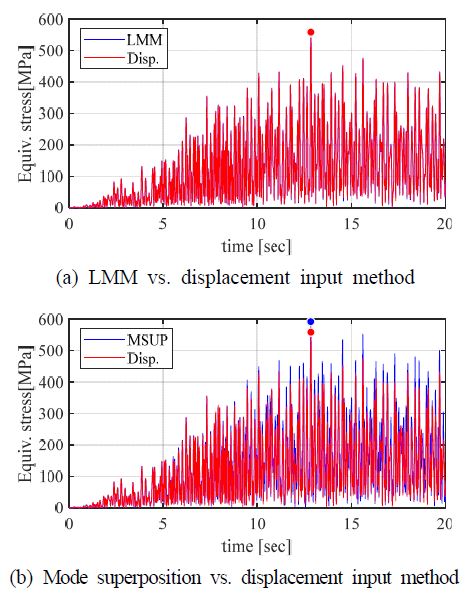
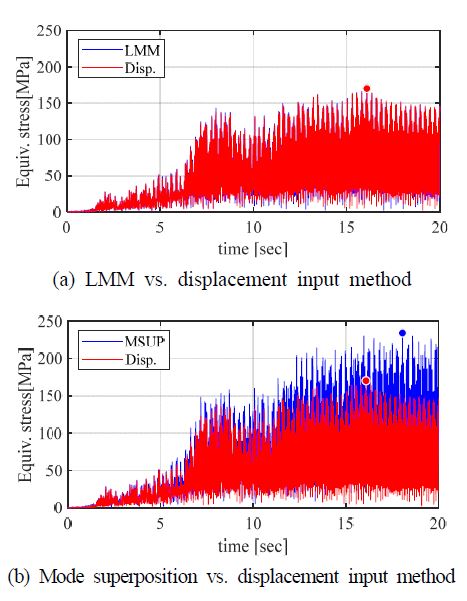
방법론에 따른 지진 해석 결과에 대한 일치성을 검증하고자 최대 응력이 나타난 지점인 취약부에 대한 시간이력 등가응력(von-mises stress)을 비교하였으며 ends supported 해석 경우는 Fig. 4, 그리고 all supported 해석 경우는 Fig. 5에 나타내었다. 또한 선도에서 지점으로 표시된 시간이력 응력 선도에 나타난 최대 응력에 해당하는 값과 최대응력이 발생한 시각을 Table 3에 나타내었다.

Fig. 4

Equivalent stresses of ends supported case

Fig. 5

Equivalent stresses of all supported case

Table 3

3Maximum equivalent stress[MPa]

Ends supported 해석 경우에 대하여 거대 질량법과 지점 변위입력 방법의 최대 응력이 발생하는 시각이 일치하며 그 경향성이 매우 유사하다. 또한 두 입력 방법에 대하여 최대 응력값의 차이가 0.5 %로 일치하는 결과가 나타난다. 이와 달리, 모드 중첩법을 이용한 가속도 입력방법은 경향성은 유사하지만 응력 분포가 변위 입력 대비 더 크게 나타남을 알 수 있다. 또한 최대 응력값을 기준으로 다른 입력 방법의 결과보다 약 6 % 크게 나타난다. 또한 ends supported 해석 경우에 대한 취약부는 1번 지지대 인근으로 모두 동일한 취약부를 갖는다.

All supported 해석 경우에 대하여 ends supported 해석 경우와 유사하게 거대 질량법과 변위입력 방법의 일치성이 높고 최대 응력이 발생하는 시각이 동일하다. 하지만 모드 중첩 방법과 변위 입력 방법 간의 최대 응력 발생 시각과 최대 응력의 크기 차이가 두드러진다. 최대 응력이 발생한 위치는 8번 곡관의 측면부로 동일하나, 최대 응력은 37.6 %의 차이를 지닌다.

정리하자면 거대 질량법과 변위 입력 시간이력 해석은 다지점 가진 시나리오 구성에 대한 응답의 일치성이 높게 나타나며, 모드 중첩 방법은 지지대의 개수가 많아질수록 오차가 더 커진다. 이러한 오차의 원인은 해석과정에서 요소가 가질 수 있는 자유도가 제한되기 때문이다. 구체적으로 full transient 해석에서의 요소가 가질 수 있는 자유도와 비교할 때, 한정된 모드 차수가 모달 좌표계로 자유도를 제한하기 때문에 transient 거동을 예측함에 있어서 오차가 발생한다. 따라서 모드 중첩 방법론을 적용한 입력 방법은 ends supported와 같은 단순한 지지대 구성을 지닌 모사 배관계에 한하여 적절한 입력 방법이 될 수 있다.

2.4 지지대 경계조건의 변경

방법론에 따른 응답의 유사성 확인을 위하여 기존의 유한요소해석 모델에서 지지대에 대한 정의는 배관에 지지대가 완전하게 결합한다는 가정 아래 지진해석을 수행하였다. 구체적으로 지지점으로 정의된 지지대의 단면에 대하여 단면의 변형을 허용하지 않고 단면에 놓인 모든 절점이 동일한 자유도를 갖도록 해석 모델을 구성하였다. 하지만 실제 지지대의 설치 및 결합조건은 다양하며, 지지대의 경계조건 설정에 따라 다른 시간이력 지진 응답이 도출될 수 있다. 따라서 대상 모사 배관계에 대하여 배관 구조물 중간에 놓인 2번 지지대에 대한 경계조건 설정을 달리하여 지진해석을 수행하였다. 구체적으로 2번 지지대의 경계조건에 대하여 단면에 놓인 각 절점에 대하여 독립적인 자유도를 가질 수 있도록 설정하여 시간이력 지진해석을 수행하였다.

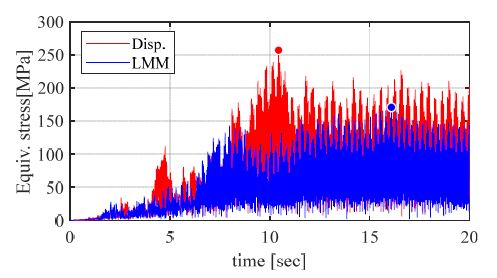
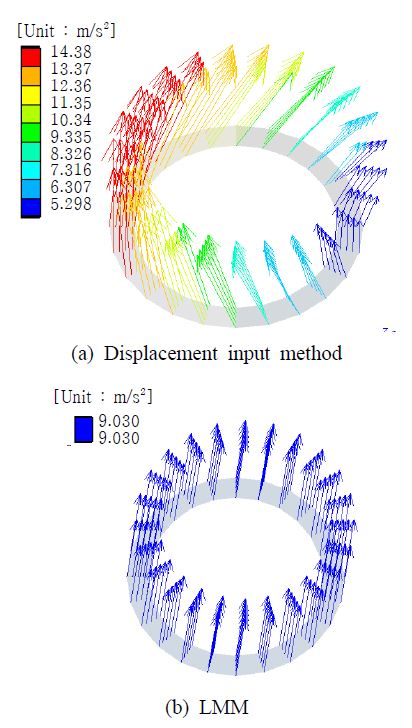
경계조건 설정을 변경한 지진 해석 경우에 대하여, 최대 응력이 발생하는 8번 곡관에 대한 등가응력 선도는 Fig. 6과 같이 나타난다. 거대 질량법의 경우 경계조건 설정을 변경하지 않은 Fig. 5(a)와 동일한 응답이 도출되는 반면, 변위 입력을 통한 시간이력해석은 경계조건 설정의 변경이 반영된 응답이 도출된다. 또한 실제 해석에서 활용된 2번 지지대 단면에 대한 가속도 분포를 Fig. 7에 나타냈다. 변위 입력 방법은 Fig. 7(a)와 같이 단면 거동이 달라졌으나, 거대 질량법에 대해서는 Fig. 7(b)와 같이 경계조건 변경 이전 시점과 일치하는 응답이 나타남을 알 수 있다. 구체적으로 변위 입력에서 나타나는 단면 거동은 단면 중심점에 대하여 3축 회전이 가능한 거동을 나타내지만 거대 질량법의 경우 회전에 대한 자유도가 반영되지 않았으며 두 대상 구조물은 서로 다른 동적인 특성을 갖는다. 따라서 배관 구조물의 동특성 변화가 반영된 변위 입력 방법에 대해서는 더 많은 자유도가 부여됨에 따라 Fig. 6에서와 같이 8번 곡관과 같은 취약부에서 국부적으로 응력 집중이 발생하여 더 큰 응답을 나타내기도 한다.

Fig. 6

Equivalent stress of all supported and changing boundary condition on support 2

Fig. 7

Acceleration distribution on support 2 of displacement input method and LMM

정리하자면 변위 입력 방법을 통해 의도하는 경계조건의 설정이 가능하며, 거대 질량법의 경우 단면 거동에 대한 자유도를 부여했음에도 완전하게 구속되어 있는 지지대를 모사한 해석 경우와 유사한 응답을 나타낸다. 따라서 다지점 가진을 고려한 배관계의 지진해석 중에서도 지지대 설치 조건에 따른 구조물의 동특성 변화를 반영하고자 할 때, 거대 질량법은 한계가 존재하며 변위 입력 방법이 적절하다고 할 수 있다.