데이터 기반 모델축소법을 이용한 효율적인 비선형 구조해석 개발

1. 서 론

다양한 공학 분야에서 대규모 자유도를 갖는 문제를 효과적으로 해결하기 위해, 차원 축소를 통한 축소 모델을 구성하는 노력이 이루어져 왔다. 이러한 차원 축소 방식은 해석의 정확도를 유지하면서 반복 계산이 요구되는 대용량 문제에 대한 효율적인 접근 방법으로 대두되고 있다. 대표적인 모델축소법인 축소 기저법(reduced basis method)으로 주성분 분석(principal component analysis, PCA)⁽¹⁾과 적합 직교 분해(proper orthogonal decomposition, POD)⁽²⁾ 등이 적용되어왔다. 나아가, 비선형 문제에 대한 효율적인 축소모델을 구성하기 위해, hyper-reduction 기법으로 경험적 보간법(empirical interpolation method, EIM)⁽³⁾ 및 이산 경험적 보간법(discrete empirical interpolation method, DEIM)⁽⁴⁾ 그리고 ECSW(energy-conserving sampling and weighting, ECSW)⁽⁵⁾와 같은 접근법이 제안되었다. 최근에는 시스템 응답 도출에 대한 효율성만 고려된 기존의 축소 기법에 대하여, 비선형 시스템 행렬 구축의 효율성을 높이기 위해 등가 강성 행렬 기법(stiffness evaluation procedure, STEP)⁽⁶⁾이 적용된 모델축소법⁽⁷⁾이 제안되었다.

최근 인공지능 기술의 급격한 발전과 함께 다양한 공학 분야에 관련 응용 연구가 활발히 이루어지고 있으며, 복잡한 해석 모델에 대해 데이터 기반의 예측 모델^(8,9)을 구축하여 효율성을 극대화하는 등의 시도가 이루어지고 있다. 특히, 반복 계산이 요구되는 최적설계 또는 비선형 해석에 효과적으로 적용할 수 있는 딥러닝/머신러닝 기반의 모델축소법은 대용량 해석에 따른 계산 비용의 한계점을 개선할 수 있는 다양한 방법론^(10-13)으로써 제시되고 있다.

나아가, 딥러닝 기술의 인공신경망(artificial neural network, ANN) 기반 모델축소법이 적용된 연구로, 차원 축소 네트워크인 오토인코더(autoencoder, AE)와 ANN의 네트워크 구조 중 하나인 다층퍼셉트론(multi-layer perceptron, MLP)을 적용하여 유동해석에 대한 축소 모델⁽¹⁴⁾을 개발하였으며, 적합 직교 분해와 합성곱 신경망(convolutional neural network, CNN)을 적용하여 비정상 유동 예측을 위한 축소 모델⁽¹⁵⁾이 개발되었다.

이 논문에서는 대표적인 모델축소법인 적합 직교 분해와 ANN 기반의 차원 축소 네트워크인 AE를 연계한 POD-AE 기반 모델축소법을 제시한다. 나아가, 축소 모델링 관점에서 보다 효율적이고 훈련 안정성이 높은 모델을 정의하기 위해 변이형 오토인코더(variational autoencoder, VAE)를 고려하였으며, 이를 기존의 AE와 비교 분석하였다.

2. POD-AE 기반 모델 축소법

2.2 POD-AE 기반 모델축소법

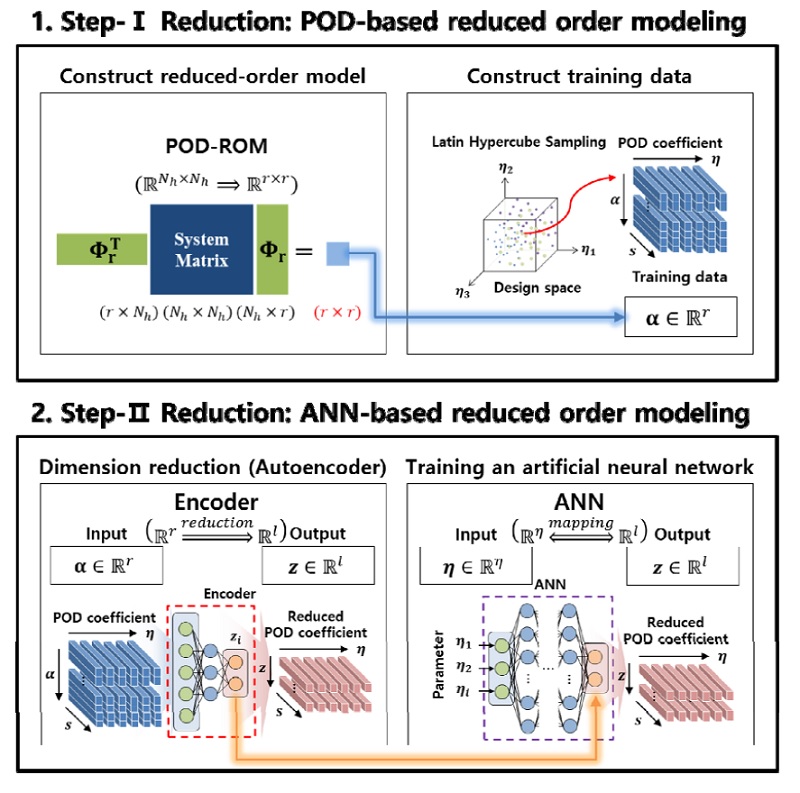
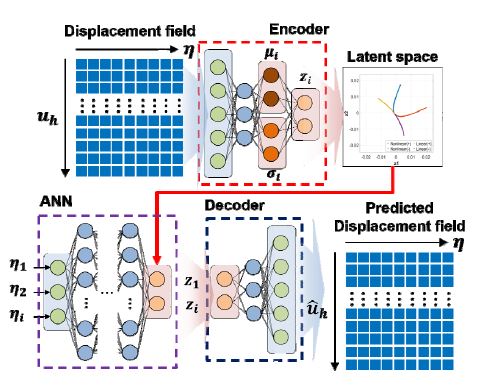
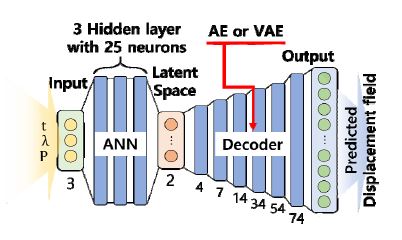
POD-AE 기반 모델축소법은 효율적인 데이터 확보 및 축소 차수 모델 구성을 위한 offline 단계와 매개변수 해석이 수행되는 online 단계로 구성된다. 이때, offline 단계는 Fig. 1과 같이 두 가지 단계의 축소 차수 모델링을 통해 수행된다.

Fig. 1

POD-AE based model order reduction with the unsupervised-supervised learning

먼저, 적합 직교 분해를 통해 축소 차수 모델을 구성하고, 이를 통해 훈련 데이터인 설계변수 변화에 따른 적합 직교 계수 α(η)를 효율적으로 확보한다. 다음으로, ANN의 대표적인 차원 축소 네트워크인 AE를 통해 한 단계 더 차원 축소를 수행하여 축소된 적합 직교 계수 z(η)를 얻는다. 마지막으로, 입력과 출력에 대한 복잡한 관계를 학습할 수 있는 ANN의 장점을 활용하여, 설계변수가 포함된 매개변수 η 입력에 대한 축소된 적합 직교 계수 z(η)를 출력하도록 훈련한다.

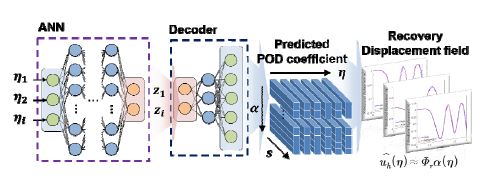
POD-AE 기반 모델축소법의 online단계는 Fig. 2에 나타내었으며, 앞서 학습된 ANN과 AE의 디코더와의 네트워크 연계를 통해 정립된다. 결과적으로, 매개변수 입력에 대하여 적합 직교 계수 α(η)를 예측하며, 전체 자유도에 대한 변위 응답으로 복원하는 과정 $$ \widehat{{\mathit{u}}_{\mathit{h}}}\left(\mathit{\eta }\right)\approx {\mathit{\Phi }}_{\mathit{r}}\mathit{\alpha }\left(\mathit{\eta }\right)$$을 거친다. 따라서 비선형 구조해석을 위한 복잡한 지배방정식 없이 매개변수 입력에 대하여 변위 응답으로의 예측이 가능하다.

Fig. 2

POD-AE based model order reduction method combined ANN and decoder

2.3 AE 기반 모델 축소

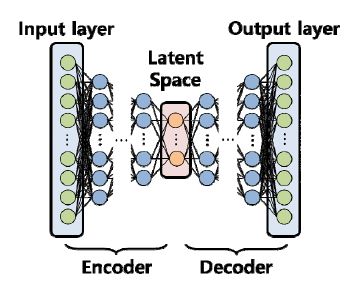
이 절에서는 전술한 POD-AE 기반 모델축소법에서 적용한 AE를 소개한다. ANN 기반의 대표적인 차원 축소 네트워크인 AE는 라벨이 되어있지 않은 훈련데이터를 사용하여 지도 없이 학습하는 비지도 학습 방법(unsupervised learning)으로 주어진 입력보다 낮은 차원을 갖는 잠재 공간(latent space)에서의 데이터의 밀집된 표현을 학습할 수 있는 ANN의 네트워크 구조 중 하나이다⁽¹⁷⁾.

Fig. 3은 AE의 기본 구조를 나타내며, 식 (3)과 같이 입력을 잠재 공간에서의 내부 표현(latent representation, code)으로 바꾸는 인코더(encoder)와, 식 (4)와 같이 내부 표현을 다시 입력과 동일한 출력으로 재구성하는 디코더(decoder)로 구성된다. 이러한 AE의 인코더-디코더 구조는 입력을 내부 표현으로 압축하고 다시 출력으로 재구성한다. 이를 통해, 인코더는 고차원의 입력 데이터를 저차원의 내부 표현인 잠재 공간으로 압축하여 입력 데이터에 대한 특징과 패턴을 찾을 수 있다. 또한, 식 (5)와 같이 입력과 출력에 대한 평균 제곱 오차(mean squared error, MSE)를 손실 함수(loss function)로 적용하고, 이를 최소화함으로써 학습이 수행된다.

$\[ \mathit{z}=f_{\varphi }\left(\mathit{x}\right) \]$

(3)

$\[ \widehat{\mathit{x}}=g_{\theta }\left(\mathit{z}\right) \]$

(4)

$\[ L_{AE}\left(\varphi ,\theta ;x^{\left(i\right)}\right)\begin{array}{l}=MSE\left(x^{\left(i\right)},{\widehat{x}}^{\left(i\right)}\right)\\ =\frac{1}{n}\sum _{i=1}^n\left( x^{\left(i\right)}-g_{\theta }\left(f_{\varphi }\left(x^{\left(i\right)}\right)\right)\right)\end{array} \]$

(5)

Fig. 3

Architecture of AE

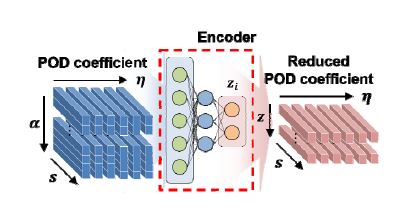
따라서 POD-AE 기반 모델축소법을 고려할 경우, 적합 직교 계수 α(η)를 AE의 입력 데이터로 적용하여, Fig. 4와 같이 잠재 공간으로 축소된 적합 직교 계수 z(η)를 얻을 수 있으며, 이는 ANN의 출력에 해당하는 훈련데이터로 사용된다.

Fig. 4

Reduced POD coefficient with encoder of AE

그러나 AE는 훈련 과정에서 난수 발생기에 의존함에 따라 형성된 잠재 공간의 분포가 매번 달라진다. 이는 2.2절에서 제시한 과정 중, 잠재 공간에서의 내부 표현을 이용한 기존 해의 추정 단계에서 어려움이 따를 수 있다. 따라서 이 연구에서는 확률론적인 접근 방법이 적용되어 잠재 공간 형성에 대한 규제가 존재하는 VAE를 고려하고자 한다.

3. VAE 기반 모델축소법

AE에서의 변형된 구조를 갖는 차원 축소 네트워크인 VAE를 통해 축소 차수 모델을 구성한다. VAE는 비지도 학습 기반의 생성 모델(generative model)의 유형 중 하나로써 확률기반의 변분 추론(variational inference)을 통해 데이터의 분포를 추론하는 네트워크이다⁽¹⁸⁾.

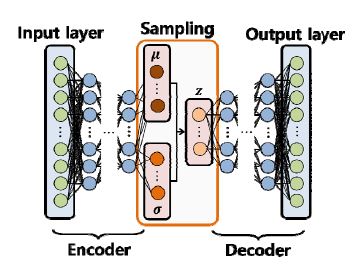
Fig. 5는 VAE의 기본 구조를 나타내며, AE의 구조에서 샘플링(sampling)이 추가적으로 존재하는 특징을 가지고 있다. VAE에서도 기존의 AE에서와 마찬가지로, 훈련 과정에서 입력에 대하여 잠재 공간으로의 압축과 이에 대한 재구성 과정을 통해 입력 데이터에 대한 특징과 패턴을 추출하며, 동시에 잠재 공간으로의 압축(또는 차원 축소) 과정을 통해 차원 축소 네트워크로써 사용될 수 있다.

Fig. 5

Architecture of VAE

VAE에서의 각 구성 요소는 확률론적인 접근 방법이 적용된다. 먼저, 인코더는 입력 데이터 x가 주어졌을 때, 내부 표현 z의 확률 분포를 추론하는데, 이는 사후 분포(posterior distribution) p_θ(z|x)를 의미하며, 이는 수학적 엄밀해를 도출하는데 어려움이 존재한다. 따라서 변분 추론 기법을 적용하여 식 (6)과 같이 인코더에서 정규 분포의 모수인 평균 μ과 분산 σ을 변수로 갖는 q_ϕ(z|x)를 도입하고 사후 분포 p_θ(z|x)를 근사한다. 다음으로 평균과 표준편차에 관한 정규분포를 따르는 내부 표현 z에 대하여 샘플링을 수행하고, 식 (7)과 같이 디코더에서 내부 표현 입력에 대한 재구성인 $$ \widehat{\mathit{x}}$$를 출력한다. 이때, 인코더에서 얻은 평균 μ, 표준편차 σ 및 가우스 정규 분포 ϵ를 통해, z = μ + σ⨀ϵ와 같은 재매개변수화 기법(reparameterization trick)이 적용된다. 이를 통해 미분이 가능해짐에 따라 훈련 과정에서의 역전파(backpropagation)⁽¹⁹⁾ 알고리즘 적용이 가능해진다.

또한, VAE는 식 (8)과 같은 손실함수를 적용하고, 이를 최소화함으로써 훈련된다. 식 (8)에서 우변의 첫 번째 항은 입력과 출력에 대한 평균 제곱 오차이며, 두 번째 항은 인코더의 실제 사후 분포와 근사한 분포와의 유사한 정도를 나타내는 척도인 쿨백-라이블러 발산(Kullback-Leibler divergence, KLD)이다. 자세한 정식화 과정은 참고문헌 19번에 제시되어 있다.

식 (8)과 같은 잠재 공간 형성에 대한 규제가 포함된 VAE를 적용하면 훈련데이터에 대한 분포를 고려한 잠재 공간을 얻을 수 있으며, 이를 통해, 앞서 설명한 AE의 난수 발생기 의존성에 대한 한계점을 개선할 수 있다. 이 연구에서는 VAE 기반 모델축소법의 적용 가능성을 분석하기 위해 완전 차수 모델의 변위 응답을 직접 이용하였으며, 이를 AE가 적용된 모델축소법과 비교하고자 한다.

VAE 기반 모델축소법은 ANN과 연계하여 Fig. 6과 같이 정립된다. 이는 비선형 문제에서 복잡한 지배방정식의 풀이 또는 비선형 항에 대한 근사 없이, VAE의 인코더에서 사전에 정의한 매개변수 공간에서의 변위 응답을 통해 직접적으로 차원 축소를 수행할 수 있다. 또한, 내부 표현은 훈련데이터의 분포를 학습하도록 하는 잠재 공간 형성에 대한 규제가 존재하는 VAE를 통해 정의되기 때문에, 보다 유의미한 내부 표현을 얻을 수 있다. 이를 통해, 매개변수 입력에 따른 내부 표현과의 관계를 학습하여 최종적으로 변위 응답을 추종하는 과정 중에서 ANN의 훈련 안정성을 도모할 수 있다.

Fig. 6

VAE based model order reduction method combined ANN and decoder

4. 수치 해석 결과

4.1 POD-AE 기반 모델축소법

(1) 문제 정의

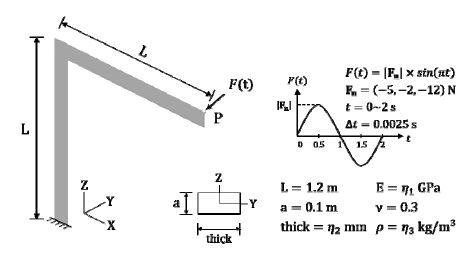
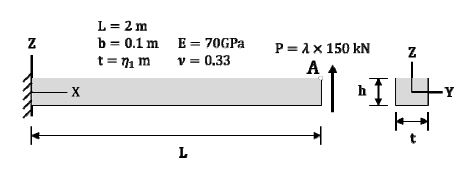
POD-AE 기반 모델축소법의 정확성과 효율성을 확인하기 위한 수치 해석 예제로 동적 하중을 받는 L-shape 프레임을 고려하였다. Fig. 7은 L-shape 프레임의 형상, 물성 및 경계조건을 나타내며, Co-rotational⁽²⁰⁾ 정식화 기반의 삼각형 shell 요소를 사용하여 8001개의 절점과 48 006개의 자유도를 갖도록 이산화하였으며, in-house code를 통해 해석을 수행하였다.

Fig. 7

Model configuration and boundary condition for a L-shape frame

나아가 매개변수 변화를 고려하기 위하여 Table 1과 같이 영률 및 밀도와 같은 재료의 특성과 두께에 대한 3차원의 설계변수 공간을 정의하였다.

Table 1

Design space for L-shape frame

(2) POD-AE 기반 모델축소법 적용

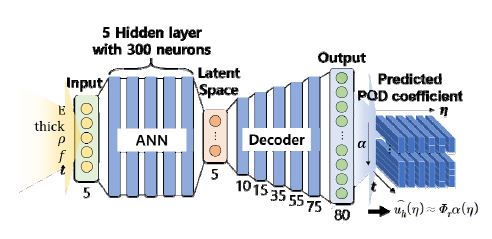
먼저, 적합 직교 분해 기반 축소 차수 모델을 구성하기 위해, Table 1에 제시된 설계변수 공간의 상한과 하한 값의 8개 조합에 대한 완전 차수 모델 해석을 수행하고 스냅샷 행렬을 구성하였다. 나아가, 스냅샷 행렬에 대한 특이값 분해를 통해 적합 직교 모드 Φ를 도출하였으며, 총 80개의 적합 직교 모드를 선정하였다. 따라서 축소 변환 행렬 Φ₈₀을 이용하여 적합 직교 분해 기반 축소 차수 모델을 구성하였고, 설계변수 변화에 따른 적합 직교 계수 α(η)를 효율적으로 획득하여 AE의 훈련데이터로 적용하였다. 다음으로 AE 훈련을 통해 80에서 5 자유도를 갖도록 차원 축소를 수행하였으며, 잠재 공간으로 축소된 적합 직교 계수 z(η)를 도출하였다. 마지막으로 설계변수(η(영률, 두께, 밀도))와 힘, 시간을 ANN의 매개변수 입력으로, 축소된 적합 직교 계수 z(η)를 출력으로 정의하여 매개변수 입력에 대한 축소된 적합 직교 계수 z(η)의 관계를 학습하였다.

앞서 학습된 ANN과 AE의 디코더와의 네트워크 연계를 통해, 최종 구성된 POD-AE 기반 모델 축소 프레임워크는 Fig. 8에 나타내었다. 따라서 POD-AE 기반 모델축소법을 통해 매개변수 입력만으로 변위 응답을 최종적으로 도출할 수 있다.

Fig. 8

Reduced-order model using POD-AE

(3) 매개변수에 따른 변위 응답 예측 비교

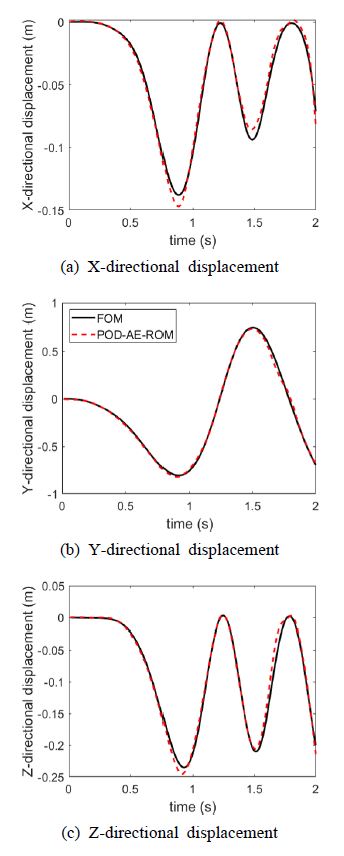
앞서 구성한 POD-AE 기반의 모델축소법(Fig. 8)을 적용하여, 완전 차수 모델(FOM)과 POD-AE 기반의 축소 차수 모델(POD-AE-ROM)에서의 변위 응답을 비교하였다. 이때, 훈련데이터에 포함되지 않은 임의의 조건인 설계 변수 η = [85, 0.003, 2670]를 매개변수 입력으로 적용하였다.

Fig. 9는 각 모델 별 X-, Y-, Z-방향의 변위 응답 결과 비교를 나타낸다. FOM과 POD-AE-ROM에서 각 방향의 변위 응답에 대하여 평균 제곱근 오차를 비교하였을 때, 최대 0.0208이내로 잘 일치하는 것을 확인하였다. 또한, POD-AE-ROM에서 소요된 해석 시간은 1.17초로 실시간 변위 예측이 가능함을 확인하였다.

Fig. 9

Comparison of the displacement history for L-shape frame

4.2 AE와 VAE 비교

(1) 문제 정의

다음으로 VAE의 적용 가능성을 확인하기 위해, 수치 해석 예제로 끝단에서 전단 하중 P를 받는 외팔보를 고려하였다. 외팔보의 형상, 물성 및 경계조건은 Fig. 10에 나타내었으며, in-house code를 통해 4절점 평면응력 요소를 사용하여 84 자유도를 갖도록 이산화하여 해석을 수행하였다.

Fig. 10

Model configuration and boundary condition for a 2-D cantilever beam

또한, Table 2와 같은 매개변수 공간에 따른 외팔보의 기하 비선형 정적해석과 선형 정적해석을 통해 변위 응답인 훈련데이터를 구성하였다. 이때, 훈련데이터는 41개의 두께 변화를 고려하였으며, 비선형과 선형, 하중의 방향에 대하여 대칭적인 훈련데이터를 구성하였다.

Table 2

Parameter space for 2D cantilever beam

(2) ANN 기반 모델축소법 비교

먼저, AE와 VAE의 인코더를 통해 총 84에서 2 자유도를 갖도록 차원 축소를 수행하였다. 각 차원 축소 네트워크의 인코더 구조는 6개의 은닉층을 가지며, 각 은닉층에서 [74-54-34-14-7-4-(2-2,VAE)]의 뉴런으로 구성하였다. 이때, 디코더는 차원 축소 네트워크의 구조적 특징에 의해 인코더와 대칭적으로 존재한다. 다음으로, 앞서 도출한 잠재 공간으로 축소된 변위 응답을 ANN의 출력으로, Table 2의 매개변수를 입력으로 정의한 ANN을 훈련하였다. 최종 구성된 ANN 기반 모델 축소 프레임워크는 Fig. 11에 나타내었다.

Fig. 11

Artificial neural network-based model order reduction framework

(3) 매개변수에 따른 변위 응답 예측

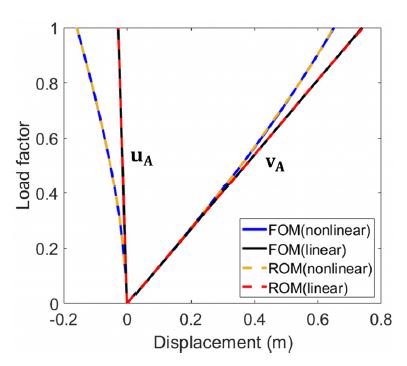
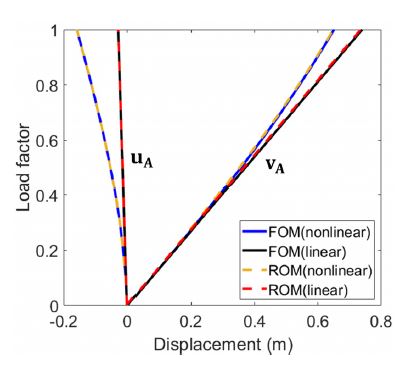
앞서 구성한 ANN 기반 모델축소법(Fig. 11)에 대하여 디코더가 AE 또는 VAE일 때의 변위 응답을 비교하였다. 이때, 훈련데이터에 포함되지 않은 임의의 조건인 두께가 t = 0.062m일 때를 매개변수 입력으로 적용하였다.

Figs. 12~13은 각각 디코더가 AE 또는 VAE일 때의 변위-하중 선도 예측 결과를 나타내며, FOM의 비선형 및 선형 해석 결과와 비교하였다. 이때, AE에서의 변위 응답은 FOM과 비교하였을 때, 최대 평균 제곱근 오차 0.012이하로 예측되었다. 또한, VAE에서는 최대 평균 제곱근 오차 0.004이하로 예측되었다. 따라서 ANN 기반 모델 축소 네트워크에서 AE와 VAE 모두 예측 성능 측면에서 좋은 결과를 보이는 것을 확인하였다.

Fig. 12

Load-displacement result from AE based model order reduction

Fig. 13

Load-displacement result from VAE based model order reduction

(4) 잠재 공간으로 축소된 변위 응답 분표 비교

각 차원 축소 네트워크 모델인 AE와 VAE에서의 잠재 공간은 각각의 인코더를 통해 입력 데이터에 대한 특징과 패턴이 밀집된 표현 즉, 내부 표현이 정의되는 공간이다. 따라서 AE와 VAE의 입력 데이터인 전체 자유도에서의 변위는 잠재 공간으로 차원이 축소된 내부 표현으로써 표현된다. 그러나 잠재 공간에서 정의되는 내부 표현은 각 네트워크에서 잠재 공간 형성에 대한 차이에 따라 서로 다르게 표현된다.

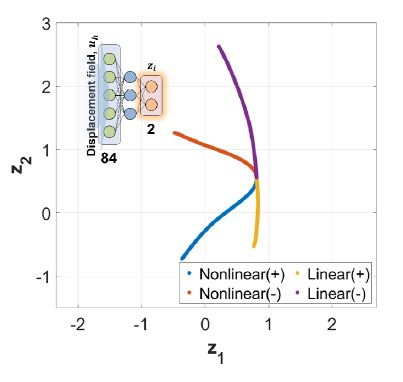
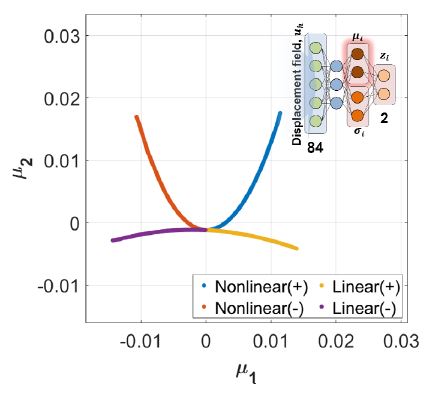
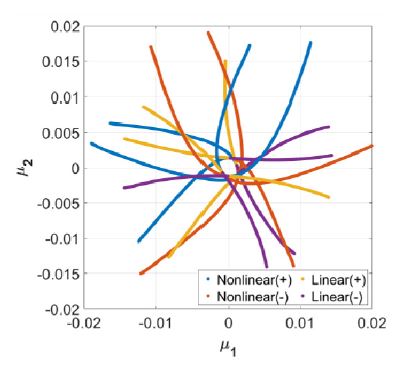
내부 표현에서 ANN의 입력 데이터인 매개변수의 특징이 충분히 포함되지 않을 때, 전술한 ANN 기반 모델축소법에서 내부 표현을 이용한 기존 해의 추정 단계에서의 어려움을 초래할 수 있다. 따라서 각 차원 축소 네트워크 모델의 인코더를 통해 도출된 내부 표현인 잠재 공간으로 축소된 변위 응답 분포를 비교하였다. 이때, Fig. 14와 Fig. 15는 각각 AE와 VAE의 잠재 공간을 나타낸다.

Fig. 14

Dimension reduction from encoder of AE

Fig. 15

Dimension reduction from encoder of VAE

각 차원 축소 네트워크 모델의 잠재 공간은 입력 데이터의 특성과 관련된 영역으로 그 분포가 형성됨을 알 수 있다. 또한, VAE의 경우(Fig. 15), 입력 데이터의 특징이 반영된 보다 정제된 형태의 잠재 공간이 도출됨을 확인하였다.

반면에 AE의 경우(Fig. 14), 난수 발생기에 의존하는 훈련 과정에서 VAE와 같은 입력 데이터와 관련된 잠재 공간 형성에 대한 규제가 없기 때문에, 입력 데이터의 특징이 드러나지 않는 것을 알 수 있다. 이를 보다 명확하게 확인하기 위해, 각 차원 축소 네트워크 모델을 반복 훈련하였다.

(5) 훈련 시도별 축소된 변위 응답 분표 비교

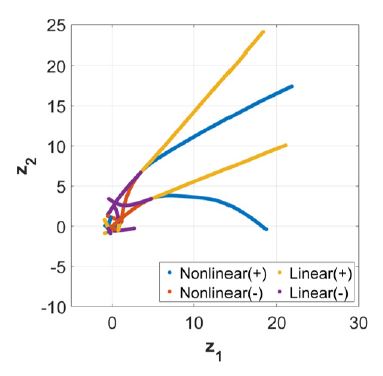
각 차원 축소 네트워크 모델을 통한 잠재 공간 형성 시 난수 발생기에 대한 의존적인 훈련 과정의 규제에 대한 영향을 확인하기 위해, 동일한 차원 축소 네트워크에 대하여 동일 조건에서 5번 반복 훈련을 수행하였다. 이를 통해, 각 네트워크의 구조적 특성에 따라 형성되는 잠재 공간의 분포를 비교하였다.

AE에서의 잠재 공간은 매 훈련 시도 마다 잠재 공간이 형성되는 분포가 달라지며, 난수 발생기에 대한 큰 의존성을 갖는 것을 알 수 있다(Fig. 16). 반면에, VAE에서의 잠재 공간은 매 훈련 시도 마다 유사한 분포의 잠재 공간이 형성되었다(Fig. 17). 따라서 AE와 VAE에서의 차이는 훈련 과정에서의 잠재 공간에 대한 규제가 존재하는 손실 함수의 존재 여부에 의해 나타나는 특징임을 확인하였다.

Fig. 16

Latent space from AE with 5-trial training procedure

Fig. 17

Latent space from VAE with 5-trial training procedure

5. 결 론

이 논문에서는 효율적인 비선형 구조해석을 위하여 데이터 기반 모델축소법으로 적합 직교 분해와 AE가 적용된 POD-AE 기반 모델축소법을 제시하였다. 여기서, L-shape 프레임에 적용하여 임의의 매개변수 입력에 대한 변위 응답을 예측하였다. 이때, 완전 차수 모델에서의 변위 응답과 최대 평균 제곱근 오차 0.0208 이하로, 기 개발 모델축소법의 정확성을 검증하였다. 또한, 해석에 소요된 시간은 1.17초로 실시간으로 변위 응답 예측하여 그 효율성을 확인하였다. 다음으로, 축소 모델링 관점에서 네트워크 훈련 안정성의 개선 가능성을 확인하기 위해, VAE 기반 모델축소법을 제시하였다. 이때, 2차원 외팔보의 정적 해석 문제에 적용하여 기존의 AE와 비교하였다. 임의의 매개변수 입력에 대하여 완전 차수 모델의 변위 응답과 최대 평균 제곱근 오차 0.012이하로 AE와 VAE 모두 예측 성능 측면에서 좋은 결과를 보였다. 그러나 최대 변위가 발생하는 지점에서 y축 방향 변위의 정확도는 전체 예측 정확도보다 상대적으로 낮았으며, 이를 개선하기 위해 VAE에 관한 hyperparameter 분석을 수행할 예정이다.

나아가, 각 차원 축소 네트워크의 잠재 공간을 비교하였다. 이때, VAE에서 입력 데이터에 대한 특징이 담긴 보다 정제된 형태의 축소된 변위 응답이 항상 같은 분포의 잠재 공간 내에서 도출되는 것을 확인하였다. 여기서 항상 같은 분포의 잠재 공간을 갖는 잠재 공간은 훈련데이터의 가감 혹은 해석 모델의 차원 증가로 인한 추가적인 훈련이 요구될 때, 잠재 공간에서의 내부 표현을 이용한 기존 해의 추정 단계에서 훈련 안정성을 개선할 수 있을 것으로 기대된다. 따라서 VAE에서 항상 같은 분포의 잠재 공간을 갖는 것을 확인함으로써, 축소 모델의 훈련 안정성을 개선할 수 있는 가능성이 존재한다. 향후 VAE과 ANN의 네트워크 연계 시, ANN의 hyperparameter 최적화를 통해, 훈련 안정성과 효율성을 확인할 예정이다. 나아가, 대용량 모델에 대한 적용 가능성을 확인하고 transient 및 steady-state 응답을 포함한 보다 긴 시간 영역 해석을 수행하여 VAE 기반 모델축소법을 보완할 예정이다.

Acknowledgments

이 연구는 2020년도 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다(No.2020R1C1C1006006).

References

• Vidal, R., Ma, Y. and Sastry, S., 2005, Generalized Principal Component Analysis (GPCA),  IEEE Transactions on Pattern Analysis and Machine Intelligence, Vol. 27, No. 12, pp. 1945~1959. [https://doi.org/10.1109/TPAMI.2005.244]
• Chatterjee, A., 2000, An Introduction to the Proper Orthogonal Decomposition, Current Science, Vol. 78, No. 7, pp. 808~817.
• Barrault, M, Maday, Y., Nguyen, N. C. and Patera, A. T., 2004, An ‘Empirical Interpolation’ Method: Application to Efficient Reduced-basis Discretization of Partial Differential Equations, Comptes Rendus Mathematique, Vol. 339, No. 9, pp. 667~672. [https://doi.org/10.1016/j.crma.2004.08.006]
• Chaturantabut, S. and Sorensen, D. C., 2010, Nonlinear Model Reduction via Discrete Empirical Interpolation, SIAM Journal on Scientific Computing, Vol. 32, No. 5, pp. 2737~2764. [https://doi.org/10.1137/090766498]
• Farhat, C., Chapman, T. and Avery, P., 2015, Structure-preserving, Stability, and Accuracy Properties of the Energy-conserving Sampling and Weighting Method for the Hyper Reduction of Nonlinear Finite Element Dynamic Models, International Journal for Numerical Methods in Engineering, Vol. 102, No. 5, pp. 1077~1110. [https://doi.org/10.1002/nme.4820]
• Muravyov, A. A. and Rizzi, S. A., 2003, Determination of Nonlinear Stiffness with Application to Random Vibration of Geometrically Nonlinear Structures, Computers & Structures, Vol. 81, No. 15, pp. 1513~1523. [https://doi.org/10.1016/S0045-7949(03)00145-7]
• Lee, J., Lee, J., Cho, H., Kim, E. and Cho, M., 2021, Reduced-order Modeling of Nonlinear Structural Dynamical System via Element-wise Stiffness Evaluation Procedure Combined with Hyper-reduction, Computational Mechanics, Vol. 67, No. 2, pp. 523~540. [https://doi.org/10.1007/s00466-020-01946-7]
• Kim, S. W., Oh, K. Y. and Lee, S. C., 2021, Physics-informed Neural Network for Estimation of Lithium-ion Battery State-of-health,  Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 2,  pp. 177~184. [https://doi.org/10.5050/KSNVE.2021.31.2.177]
• Nguyen, A. T., Han, J. H. and Nguyen, A. T., 2017, Application of Artificial Neural Networks to Predict Dynamic Responses of Wing Structures due to Atmospheric Turbulence, International Journal of Aeronautical and Space Sciences, Vol. 18, No. 3, pp. 474~484. [https://doi.org/10.5139/IJASS.2017.18.3.474]
• Lee, S., Jang, K., Cho, H., Kim, H. and Shin, S., 2021, Parametric Non-intrusive Model Order Reduction for Flow-fields Using Unsupervised Machine Learning, Computer Methods in Applied Mechanics and Engineering, Vol. 384, 113999. [https://doi.org/10.1016/j.cma.2021.113999]
• Im, S., Lee, J. and Cho, M., 2021, Surrogate Modeling of Elasto-plastic Problems via Long Short-term Memory Neural Networks and Proper Orthogonal Decomposition, Computer Methods in Applied Mechanics and Engineering, Vol. 385, 114030. [https://doi.org/10.1016/j.cma.2021.114030]
• Kast, M., Guo, M. and Hesthaven, J. S., 2020, A Non-intrusive Multifidelity Method for The Reduced Order Modeling of Nonlinear Problems, Computer Methods in Applied Mechanics and Engineering, Vol. 364, 112947. [https://doi.org/10.1016/j.cma.2020.112947]
• Lee, K. and Carlberg, K. T., 2020, Model Reduction of Dynamical Systems on Nonlinear Manifolds Using Deep Convolutional Autoencoders, Journal of Computational Physics, Vol. 404, 108973. [https://doi.org/10.1016/j.jcp.2019.108973]
• Xu, J. and Duraisamy, K., 2020, Multi-level Convolutional Autoencoder Networks for Parametric Prediction of Spatio-temporal Dynamics, Computer Methods in Applied Mechanics and Engineering, Vol. 372, 113379. [https://doi.org/10.1016/j.cma.2020.113379]
• Wu, P., Sun, J., Chang, X., Zhang, W., Arcucci, R., Guo, Y. and Pain, C. C., 2020, Data-driven Reduced Order Model with Temporal Convolutional Neural Network, Computer Methods in Applied Mechanics and Engineering, Vol. 360, 112766. [https://doi.org/10.1016/j.cma.2019.112766]
• Cho, H., Kim, H. and Shin, S. J., 2020, Efficient Gird Deformation Using Deterministic Sampling-based Data Reduction, International Journal for Numerical Methods in Engineering, Vol. 121, No. 18, pp. 4028~4049. [https://doi.org/10.1002/nme.6425]
• Geron, A., 2019, Hands-on Machine Learning with Scikit-learn, Keras, and TensorFlow: Concepts, Tools, and Techniques to Build Intelligent Systems, pp. 674~715, O’Reilly Media, California.
• Kingma, D. P. and Welling, M., 2013, Auto-encoding Variational Bayes, ArXiv Prepr. ArXiv1312.6114.
• Werbos, P. J., 1990, Backpropagation through Time: What It Does and How to Do It, Proceedings of the IEEE, Vol. 78, No. 10, pp. 1550~1560. [https://doi.org/10.1109/5.58337]
• Cho, H., Kim, H. and Shin, S. J., 2018, Geometrically Nonlinear Dynamic Formulation for Three-dimensional Co-rotational Solid Elements, Computer Methods in Applied Mechanics and Engineering, Vol. 328, pp. 301~320. [https://doi.org/10.1016/j.cma.2017.08.037]