구조-음향 연성 시스템의 진동모드에 의한 소음 예측

1. 서 론

구조진동은 구조체가 결합된 음환경에 따라 음영역에 고유의 음장을 형성한다. 음영역과 구조체의 경계면에서 진동과 유체의 상호작용에 의하여 유발된 음장은 연성 정도에 따라 다르지만 각각 독립적인 영역에서의 진동과 음장과는 또 다른 음장이 발현하게 된다. 공동주택에서 발생하는 중량충격음은 구조-음향 다중 물리공간에서 발생하는 대표적인 구조기인 음압으로 구조체(슬래브)의 진동에 의해 유발된다는 점에서 두 물리량 간의 강한 상관성을 가지는 것으로 예상되고 있다.

구조-음향이 연계된 음영역에서 구조체의 진동으로 음압 또는 소음을 예측하는 것은 음환경(크기 및 형상, 음경계조건)에 따라 불확실성이 내재하지만, 진동계측의 용이성, 진동량에 의한 포괄적 소음규제나 소음알람기능 등의 측면에서 두 물리량 간의 상관성을 도출하는 것은 매력적인 연구 대상으로 인식되어 왔다. 또한, 바닥충격음 사후확인제도 도입과 관련하여 설계단계에서 바닥충격음을 예측하고 이에 따른 소음저감 방안을 수립하는 기법으로 바닥 진동에 의한 수음실 소음예측의 필요성은 증대하고 있다.

슬래브 진동과 그에 의한 소음과의 상관성에 근거하여 계측된 슬래브 진동으로 소음을 예측하고자 하는 연구가 있다^(1,2). 이들 연구는 진동레벨과 소음레벨의 상관성을 추정한 것으로 경량충격음의 경우 0.95 내외의 매우 높은 상관계수를 가지는 것으로 나타나고 있다. 그에 비해 중량 충격음의 상관계수는 0.46 ~ 0.9 사이로 편차가 크게 나타나고 있으며, 그 결과 가속도레벨을 층간소음 법적기준에 대한 판단기준 데이터로 활용하는 것은 정확도 측면에서 한계가 있음을 제시하고 있다. 중량충격음의 진동 상관성 개선을 위해 진동모드와 음향모드 관계를 이용한 연구가 있다⁽³⁾. 자유장에서의 진동과 음압레벨의 상관성은 0.91로 매우 높은 상관성을 가지는 것으로 나타났으나 구조-음향이 연계된 공간에서는 진동레벨과 음압레벨의 상관관계는 모드응답의 기여도, 구조체가 포함된 음환경의 모달특성과 연관된 불확실성에 따라 달라짐을 보였다. 기존 연구를 보면, 구조진동과 음영역 소음의 연관성을 파악하고자 하는 시도는 있었지만 여전히 두 물리량 사이의 정량적인 인과관계는 제시되지 못한 실정이다.

이 연구에서는 구조-음향이 연계된 시스템으로부터 구조진동이 소음로 발현되는 메커니즘을 분석하고, 진동 모달인자뿐만아니라 음환경이 반영된 음향 모달인자를 이용하여 이들이 수음실의 음향모드 형성에 미치는 영향을 평가함으로써 구조진동모드로부터 수음실 소음을 예측하는 기법을 제시한다. 구조진동-음향모드응답 예측의 정합성을 평가하기 위하여 시간영역 수치해석을 수행하였다. 진동수 영역 해석은 정상상태(stationary)의 음장해석에 적합한 반면, 충격하중에 의한 진동이나 이로부터 유발되는 음압(중량충격음과 같은 non-stationary 신호)특성을 반영하기 위해서는 시간영역해석이 적합하기 때문이다. 또한 시간영역해석은 시간이력 raw data를 확보할 수 있으므로 충격하중에 대한 최대진동, 최대음압과 같은 최대응답을 제공하며, 최대응답 발생지점 시간대역에 대한 1/3 옥타브 밴드 스펙트럼해석과 같은 2차 해석에 의해 최대 가속도레벨, 음압레벨을 용이하게 산정할 수 있다.

수치해석은 한 면의 일부가 셸 구조를 가지는 잔향실을 대상으로 수행하였다. 잔향실은 이상적인 음경계조건을 제공함으로써 진동과 소음의 관계를 명료하게 고찰할 수 있어 수치해석 대상으로 설정한 것이며, 셸 구조는 충격하중에 의하여 진동을 유발하고 잔향실에 중량충격음이 발현되도록 모사한 것이다.

수치해석에 의해 셸, 잔향실 계측위치로부터 진동, 음압 시간이력을 추출하고 이에 모드분해법을 적용하여 진동모드와 음향모드를 각각 구한 후 이 연구에서 제안된 진동의 음향모드 형성특성과 소음 예측기법을 검증하였다.

2. 음향모드 발현특성

2.2 진동모드에 의한 음영역 소음 예측

만약 진동모드를 알고 있다면, 인접 음향모드는 식 (8b)의 라플라스 변환을 통하여 다음과 같이 나타낼 수 있다.

$\[ q\left(s\right)=\frac{{\rho }_a{g}_a}{F_a\left(s\right)}\ddot{\eta }\left(s\right) \]$

(11)

즉, 진동모드(가속도)를 입력으로 사용하는 단자유도 시스템의 응답이 음향모드가 되는 것을 알 수 있다.

진동모드 또는 음향모드는 특정진동수(고유진동수부근)에서 큰 스펙트럼을 가지며 해당 진동수 부근의 파워 스펙트럼의 합이 진동 또는 음향의 크기를 나타낸다고 볼 수 있다. 그러므로 진동모드, 그로부터 유도된 음향모드의 분산은 식 (12)와 같이 나타낼 수 있다. 이 분산은 가속도 레벨, 또는 음압레벨을 산정하는데 사용할 수 있다.

$\[ E\left[\ddot{ \eta }\left(s\right)\ddot{\eta }\left(\tilde{s}\right) \right]={\int }_{}^{}{\left|\ddot{\eta }\left(w\right)\right|}^{2}dw \]$

(12a)

$\[ E\left[q\left(s\right)q\left(\tilde{s}\right)\right]={\rho }_a^2{g}_a^2{\int }_{}^{}{\left|\frac{\ddot{\eta }\left(w\right)}{F_a\left(w\right)}\right|}^{2}dw \]$

(12b)

여기서 E[ ]는 평균화기호, s = iw이고 w는 각속도이다. 식 (12a,b)에 각각 식 (9a,b)를 대입하여 직접 진동, 음향모드의 분산을 구할 수 있다. 특히 식 (9a,b)의 외부하중이 이상적인 충격하중이라고 가정하면 최고차항이 s에 관한 4차 방정식으므로 closed form으로 분산을 구할 수 있다⁽⁷⁾. Closed form으로 나타내면, 식 (12)의 진동모드와 음향모드의 분산은 각각의 고유진동수와 감쇠비 그리고 연성효과를 나타내는 g_s, g_a값을 포함한 변수로 이루어진다. 이들 변수를 이용하여 진동, 음향모드의 분산을 구하고 이로부터 진동, 음향모드의 가속도, 음압레벨을 구함으로써 두 모드간의 상관성을 진동수 영역에서 파악할 수 있게 된다.

음영역에 포함된 구조체의 면밀도가 음영역 매질의 밀도에 비하여 매우 큰 경우에는 연성효과가 미약하게 된다. 아파트의 슬래브와 같이 매우 비대한 질량체는 인접공기의 음압 영향이 작아 연성효과가 떨어질 수 있다. 이와 같이 구조체와 음영역의 연성효과가 작아서 무시할 수 있고 구조체의 진동만이 음영역의 음장을 유발하다고 가정하면, 더욱 간략히 진동모드, 음향모드의 분산을 구할 수 있다.

음장이 구조체에 미치는 영향을 무시하면 식 (8a)의 g_s = 0으로 할 수 있고, 진동이 음영역에 일방향으로 영향(in cascade)을 미친다고 볼 수 있으므로 식 (8b)의 g_a를 유지함으로써 다음과 같이 진동모드와 음향모드를 나타낼 수 있다.

$\[ \ddot{\eta }\left(s\right)=\frac{s^2}{F_s\left(s\right)}X\left(s\right) \]$

(13a)

$\[ q\left(s\right)=\frac{{\rho }_a{g}_a{s}^2}{F_s\left(s\right)F_a\left(s\right)}X\left(s\right) \]$

(13b)

구조체에 작용하는 이상적인 충격하중으로써 하중의 스펙트럼이 특정 진동수영역(low-upper bound, w_L < w < w_U)에서 일정한 값을 가지는 형태(band-limited white noise)로 가정하면 식 (14)와 같다.

$\[ S_{xx}\left(w\right)={\left|X\left(iw\right)\right|}^2=S_o\left(\mathrm{c}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{t}\right) \]$

(14)

이러한 충격하중에 대한 가정에 근거하여 식 (13a, b)를 각각 식 (12a,b)에 대입하여 적분하면 식 (15)와 같이 closed form으로 진동모드와 음향모드의 분산을 구할 수 있다⁽⁷⁾.

$\[ \begin{array}{l}E\left[\ddot{\eta }\left(s\right)\ddot{\eta } \left(\tilde{s}\right)\right]=S_o{\int }_{}^{}{\left|\frac{{\left(iw\right)}^2}{F_s\left(iw\right)}\right|}^{2}dw\\ =\frac{\pi S_o}{2}\frac{w_s\left(1+{4\xi }_s^2\right)}{{\xi }_s}\simeq \frac{\pi S_o}{2}\frac{w_s}{{\xi }_s}\end{array} \]$

(15a)

$\[ E\left[q\left(s\right)q\left(\tilde{s}\right)\right]\begin{array}{l}=S_o{\int }_{}^{}{\left|\frac{{\rho }_a{g}_a{\left(iw\right)}^2}{F_s\left(iw\right)F_a\left(iw\right)}\right|}^{2}dw\\ =\pi S_o{\rho }_a^2{g}_a^2\frac{N}{D}\end{array} \]$

(15b)

여기서, N = 2w_sw_a (ξ_sw_a +ξ_aw_s)

$\[ D=\begin{array}{l}4{\xi }_s{\xi }_a{w}_s{w}_a\left[{\left(w_a^2-w_s^2 \right)}^2\right.\\ \left.+4w_s{w}_a\left(w_s{w}_a\left({\xi }_s^2+{\xi }_a^2\right)+{\xi }_s{\xi }_a\left(w_s^2+w_a^2\right)\right)\right]\end{array} \]$

진동모드 분산에 대한 음향모드의 분산 비율(R)은 식 (16)과 같다.

$\[ R\left({\xi }_s,{\xi }_a,w_s,w_a,g_a\right)={\rho }_a^2{g}_a^2\frac{{\xi }_s}{w_s}\frac{N}{D} \]$

(16)

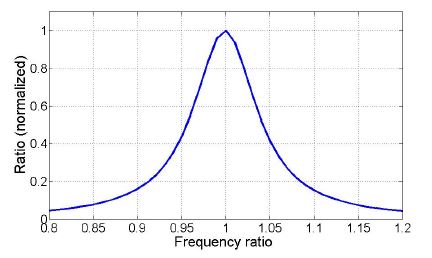
Fig. 1은 식 (16)에 의해 진동모드에 대한 음향모드의 고유진동수의 비율(w_a/w_s)로 나타낸 정규화된 분산 비율이다. 그림에서와 같이 음향모드의 진동수가 진동모드의 진동수에 벗어날수록 비율이 줄어들고 있으며, 진동수비가 5 %의 차이를 가질 때 최대분산비율의 40 %정도 되는 것을 알 수 있다.

Fig. 1

Covariance ratio

만약 진동모드가 음향모드와 매우 인접하여서 w_a = w_s라 가정하면 최대분산비율 식 (17)과 같다.

$\[ R\left({\xi }_s,{\xi }_a,w_s=w_a,g_a\right)=\frac{{\rho }_a^2{g}_a^2}{4w_s^4{\xi }_a\left({\xi }_s+{\xi }_a\right)} \]$

(17)

그러므로 식 (18)과 같이 진동모드 분산으로부터 음향모드 분산을 예측할 수 있다.

$\[ E\left[q\left.\left(s\right)\right)q\left(\tilde{s}\right)\right]=RE\left[\ddot{\eta }\left(s\right)\ddot{\eta }\left(\tilde{s}\right)\right] \]$

(18)

앞서 언급한 바와 같이 비율 R은 진동모드 고유진동수와 감쇠비, 음향모드 고유진동수와 감쇠비 및 연성계수 g_a에 의하여 결정되며, 특히 음향모드의 감쇠비가 큰 영향을 미친다. 그러므로 잔향실과 같이 감쇠가 작은 음영역에서는 같은 진동에 대해서 큰 음압이 유발되는 것을 예상할 수 있다.

3. 시간영역 연성 해석

3.1 구조-음향 연성시스템 모델링

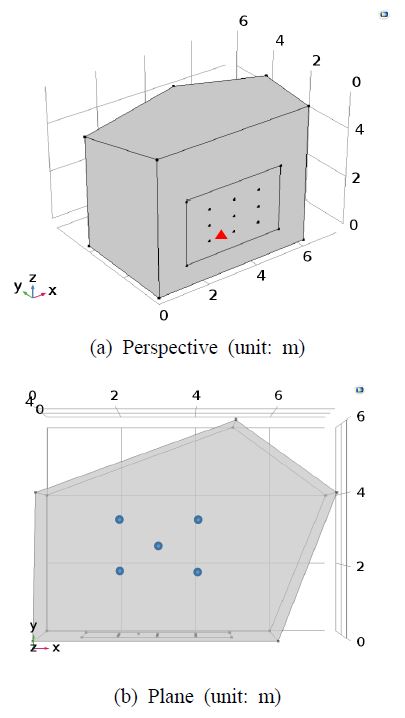
구조-음향 연성시스템으로 잔향실의 한 면 일부가 셸로 구성된 시스템을 설정하였다. 시간영역 연성해석은 COMSOL 프로그램을 사용하였으며, 모델링된 대상구조물이 Fig. 2에 나타나 있다. Fig. 2(a)는 잔향실 한 면에 포함된 셸(3.8 m × 2.6 m)을 나타내며, 셸 평면의 가로 세로 4등분 교차점 중 내부 9개의 가속도계 설치 위치와 셸 좌하부분에 삼각형으로 가진 점이 표시되어 있다. Fig. 2(b)는 잔향실 평면을 나타내는 것으로 5개의 마이크로폰 위치(높이 1.2 m)가 표시되어 있다.

Fig. 2

Modeling of reverberation chamber

Table 1은 모델링에 사용된 재료의 물성이다. 10 Hz 대역부터 진동 거동을 보기 위하여 셸의 두께를 조정하여 1차 고유진동수를 약 17 Hz 정도로 맞추었다. 셸의 감쇠는 레일리히 감쇠의 α, β 을 이용하여 10 Hz ~ 100 Hz 대역의 모달감쇠비가 2.5 % ~ 4.5 %가 되도록 설정하였다. 잔향실의 감쇠는 임피던스(벽면)로 구현하였으며, 음속의 400배로 설정하였다.

Table 1

Material properties

Table 2는 해석에 사용된 FEM 모델의 요소, mesh 최대크기와 시간이력 해석을 위한 시간간격 등을 나타내고 있다. Mesh의 크기를 이용하여 구한 유효 해석 진동수 범위는 약 170 Hz 까지이다. 충격하중은 이 연구진이 보유하고 있는 임팩트햄머를 벽체에 타격했을 때 실측한 하중 시간이력을 모사한 것이다. 해석을 위해 최대크기 400 N의 지속시간 20 msec의 사인파(sine wave)의 반파형태의 펄스로 이상화하였다. 가진 위치는 앞서 언급한 바와 같이 Fig. 2(a) 셸의 좌하영역에 삼각형으로 표시되었다.

Table 2

FEM model and analysis condition

3.2 연성 해석

(1) 모드 해석

구조-음향연성 FEM모델에 대한 고유치 해석 결과를 Table 3에 나타내었다. 연성효과가 고유값에 미치는 영향을 나타내기 위하여 셸과 잔향실이 독립적인 상태에서의 고유값과 연성된 상태에서의 고유값을 편의상 12개 이내로 비교한 것이다.

Table 3

Eigenvalues

Table 3에서 감쇠비는 허수부를 실수부로 나누면 구할 수 있다. 셸의 모드 감쇠비는 지정한 바와 같이 2.5 % ~ 4.5 % 사이, 음향모드의 감쇠비는 0.2 % ~ 0.4 %의 값을 가진다. Table 3에서 연성효과를 가지는 고유값을 보면 구조체 발현 고유값(굵은글씨 밑줄)은 고유진동수와 감쇠비가 모두 감소하는 경향을 나타내나 그 차이는 매우 작다. 연성된 음향모드의 경우 고유진동수는 큰 차이가 없으며, 감쇠비 또한 저차 음향모드를 제외하고는 큰 차이가 없다. 고유진동수, 감쇠비의 미소한 변화는 음향모드와 인접 진동모드의 연성효과에 의해 식 (10)과 같이 4차 다항함수의 해가 변화되기 때문이다. 또한, 음향모드의 감쇠비가 증가하는 것은 10배 이상 큰 진동모드 감쇠비가 음향모드의 감쇠비 증가를 견인하기 때문이다.

(2) 시간이력 해석

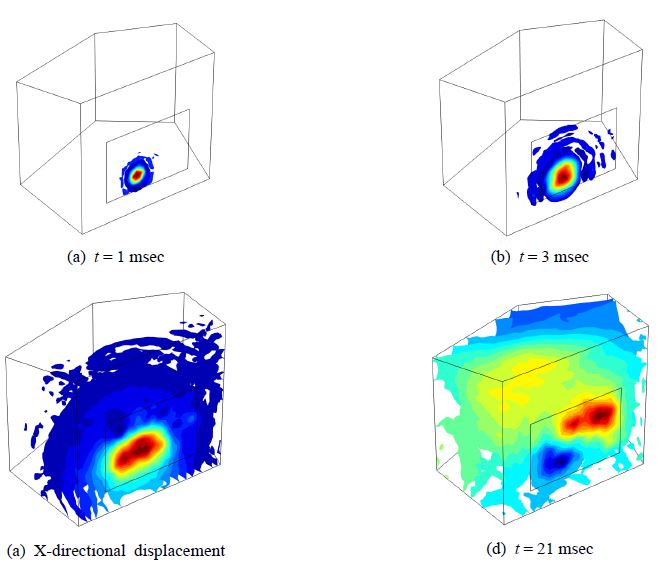
충격하중에 의한 셸 진동이 잔향실의 음압변화를 야기한다. Fig. 3은 시간에 따라 잔향실내 음압 전파 과정을 COMSOL의 isosurfaces 기능을 이용하여 도시한 것이다. 충격 후 t = 1 msec 경과 시, 셸 평면의 좌하 충격부분의 음압이 국부적으로 발생하다가 t = 3 msec를 지나 t = 9 msec에서는 셸의 크기를 넘어 잔향실 전반부로 확산되며, t = 21 msec에서 잔향실 전체로 확산되는 것을 볼 수 있다.

Fig. 3

Propagation of pressure

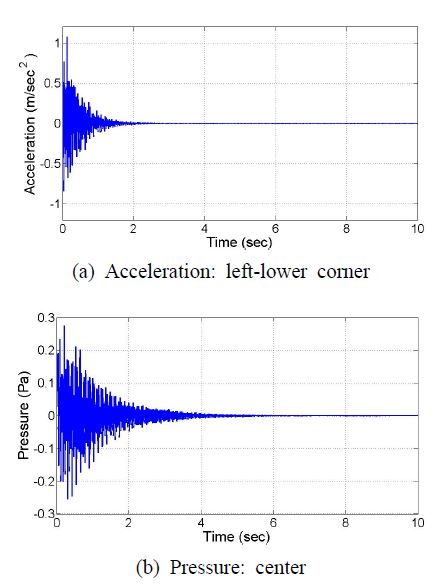
Fig. 4는 Fig. 2에 나타나 있는 가속도계, 마이크로 폰 위치에서의 가속도와 음압의 시간이력을 나타내고 있다. Fig. 4(a)는 셸 평면 좌하 모서리 부분의 가속도 시간이력이며, Fig. 4(b)는 중앙부에 설치된 마이크로폰의 음압 시간이력이다. 가속도 응답은 자유진동의 형태이며 2 초 이내에서 유지되지만, 음압의 경우 5 초까지 지속되는 것을 알 수 있다. 이것은 잔향실의 특성상 큰 임피던스에 의해 음영역의 감쇠비가 작기 때문인 것으로 사료된다.

Fig. 4

Time history

3.3 해석에 의한 음향모드 예측

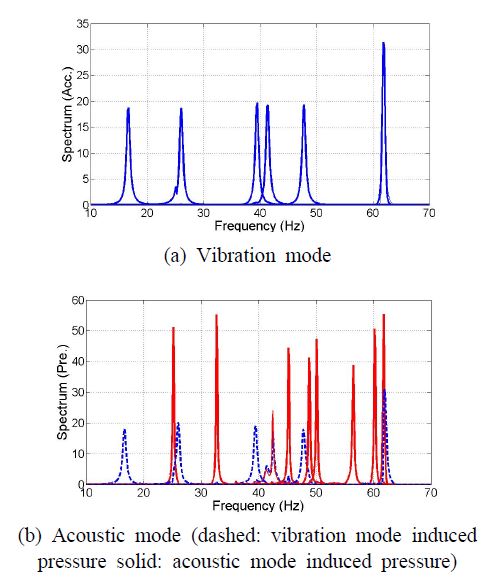
수치해석을 통해서 얻어진 9개의 가속도, 5개의 음압 시간이력에 모드분해법을 적용하여 진동모드와 음향모드를 추출하였다⁽⁸⁾. Fig. 5는 분해된 진동, 음향모드 시간이력에 푸리에 변환에 의해 10 Hz ~ 70 Hz 대역의 파워 스펙트럼으로 표현한 것이다. Fig. 5(a)는 진동모드(가속도)의 스펙트럼을 나타내는 것으로 매우 안정적인 모드분해가 이루어지는 알 수 있다. 음압에 의한 진동모드의 영향이 작아 스펙트럼의 형상에 큰 변화가 없다. 이것은 식 (9a)에서와 같이 연성효과가 작으면(g_s = 0) 분자 분모의 F_a(s)가 소거되어 단자유도 전달함수만 남기 때문이다.

Fig. 5

Power spectrum of modes

Fig. 5(b)는 음향모드의 스펙트럼을 나타낸다. Dashed line은 진동모드가 직접적으로 음압으로 전이(vibration mode induced pressure)된 것이며, solid line은 진동모드에 의하여 유발된 음향모드에 의해 발현된 음압(acoustic mode induced pressure)이라고 볼 수 있다. 음향모드 감쇠비가 진동모드 감쇠비에 비해 작으므로 스펙트럼이 좀 더 첨도가 크게 나타난다. Fig. 5(b)에서 40 Hz가 약간 초과하는 진동수 대역에서 음압 스펙트럼이 매끄럽지 못한 것은 이 연구에서 채용한 모드분해법에 의하여 진동모드와 음향모드가 인접하여 완전하게 분해가 되지 못한 것 때문이다.

Fig. 5(b)의 음압 스펙트럼에서 음향모드 외에 진동모드가 나타나는 것은 식 (9b)에서 보는 바와 같이 음향모드가 2자유도 시스템으로 표현되며 이것이 각각 2개의 단자유도(진동모드와 음향모드)로 분해되어 음압에 기여하기 때문인 것으로 사료된다.

앞서 언급한 바와 같이 진동모드는 인접한 음향모드에 영향을 미친다. 실제로 진동모드는 모든 음향모드에 영향을 미치지만 두 모드의 고유진동수가 멀리 떨어져 있으면 Fig. 1에서 보는 바와 같이 그 영향력이 급격히 줄어들므로 진동모드에 이웃한 음향모드만을 고려하는 것이다.

분해된 진동모드로부터 음향모드가 예측이 되는 지 검증하기위한 해석을 수행하였다. 이를 위하여 Table 3의 shell only 5차 진동모드(47.871 + 1.4390i)와 이웃한 acoustic only 6차 음향모드(48.826 + 0.14361i)를 대상으로 선정하였다. 이 두 모드는 연성효과에 의하여 Table 3의 coupled 고유값(47.822 + 1.4333i, 48.829 + 0.14539i)을 생성한다.

진동모드의 시간이력을 알고 있으므로, 이를 식 (8b)의 미분방정식의 입력으로 해석하여 음향모드의 시간이력을 구하고 이를 분해된 음향모드와 비교함으로써 예측 가능성을 검증하였다.

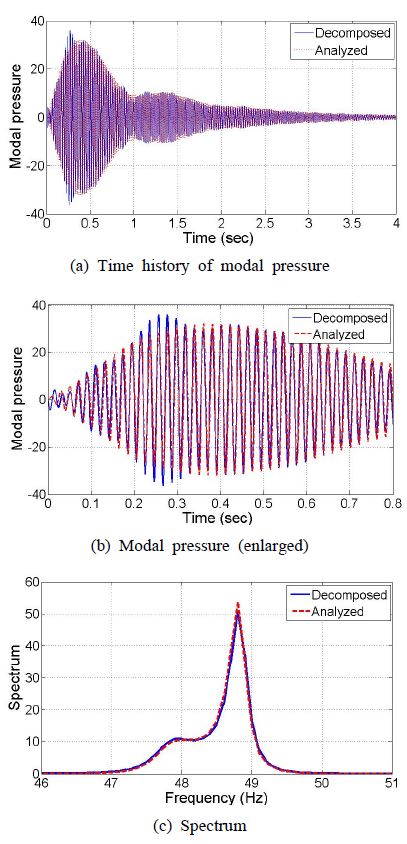
Fig. 6은 음향모드의 시간이력과 스펙트럼을 나타내고 있다. Fig. 6(a)는 계측음압으로부터 분해된 음향모드와 진동모드로부터 해석된 음향모드를 비교한 것이며, Fig. 6(b)는 최대음압이 발생하는 부분을 확대하여 비교한 것으로 매우 유사한 것을 알 수 있다. Fig. 6(c)는 스펙트럼을 비교한 것으로 음향모드의 예측이 신뢰성 있게 이루어진 것을 알 수 있다.

Fig. 6

Comparison of acoustic mode

이상과 같은 시뮬레이션을 통하여 구조체의 진동모드로부터 음향모드 예측이 가능함을 알 수 있다. 정교한 음향모드 예측을 위해서는 음영역에서 발생하는 고유의 음향특성(음향모드의 고유진동수 및 감쇠비)이 필요하다. 이 연구에서는 음영역(잔향실)에 대한 고유치해석을 통하여 음향특성을 이용할 수 있었지만, 실제 음환경에서는 이들 값을 추정할 수 있는 기술이 요구된다. 특히 음향모드의 감쇠비는 진동모드로부터 음향모드를 예측하는 매우 중요한 요소로써 음경계의 임피던스, 잔향시간 등으로부터 감쇠비를 추정하는 실험이나 기법 등의 요소기술개발을 위한 지속적인 연구가 요구된다.

4. 결 론

이 연구에서는 구조체와 결합된 음영역의 음압을 구조체의 진동으로부터 예측하기 위한 진동-음향모드의 연관성을 제시하고, 시간영역 구조-음향연성 시뮬레이션을 통해 진동모드로부터 음향모드 예측이 가능함을 검증하였다.

이상적인 음경계조건을 제공하는 잔향실에 대한 FEM해석에 의해 계측된 셸 진동과 음압에 모드분해법을 적용하여 진동모드와 음향모드를 각기 구하고 두 모드 사이의 연관성에 의해 진동모드로부터 음향모드의 예측이 이루어지는 것을 확인하였다. 보다 정밀한 음향모드 예측을 위해서는 해당 음향모드의 고유진동수와 감쇠비가 필요하며, 특히 음경계 영역으로부터 감쇠비를 구하는 것이 요구된다.

이 연구에서 제시된 음향모드 예측기술을 구조체 가속도레벨로부터 중량충격음 음압레벨 예측으로 확대하기 위해서는 계측 센서의 수, 각 모드의 진동 및 음압기여도와 음영역의 모달특성 파악을 위한 현장실험기술이 요구되며, 이에 대한 지속적인 연구가 이루어져야 할 것으로 사료된다.

Acknowledgments

이 연구는 국토교통부 국토교통기술촉진연구사업의 연구비 지원(21CTAP-C164107-01)과 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(2020R1F1A1070349).

References

• Song, M. J. and Kim, S. W., 2000, An Experimental Study on the Relationship between VAL in Mini-laboratory and SPL in Reverberation Room: Focused on the Floor Covering PVC, Journal of Architectural Institute of Korea, Vol. 16, No. 1, pp. 585~591.
• Kim, T. M., Bae, J. Y. and Yang, H. S., 2020, The Study on Characteristic of Floor Impact Noise Using the Structural Vibration on Floor Slab: Effective Plate, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 3 pp. 276~285. [https://doi.org/10.5050/KSNVE.2020.30.3.276]
• Hwang, J. S., Lee, K. S., Lee, T. J., Park, H. J. and Park, S. H., 2016, Participation Effect of Vibration Mode of Concrete Slab on Heavy Weight Floor Impact Noise, Journal of the Regional Association of Architectural Institute of Korea, Vol. 18, No. 6, pp. 127~134.
• Fahy, F., 1987, Sound and Structural Vibration: Radiation, Transmission and Response, Academic Press Inc. [https://doi.org/10.1115/1.3269418]
• Kim, T. C., Kang, S. J. and Seo, J. B., 1994, Noise Reduction of a Vehicle Acoustic Cavity Sample Using Coupled Structural-acoustic Finite Element Analysis, Proceedings of the KSNVE Annual Autumn Conference, pp. 288~294.
• Sakuma, T., Sakamoto, S. and Otsuru, T., 2014, Computational Simulation in Architectural and Environmental Acoustics: Methods and Application of Wave-based Computation, Springer, Tokyo. [https://doi.org/10.1007/978-4-431-54454-8]
• Crandal, S. H. and Mark, W. D., 1973, Random Vibration in Mechanical Systems, Academic Press, New York.
• Belouchrani, A., Abed-Meraim, K. and Cardoso, J.-F., 1997, A Blind Source Separation Technique Using Second-order Statistics, IEEE Transactions on Signal Processing, Vol. 45, No. 2, pp. 434~444. [https://doi.org/10.1109/78.554307]