[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 31, No. 6, pp.642-653

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Dec 2021

Received 06 Sep 2021 Revised 05 Oct 2021 Accepted 01 Nov 2021

DOI: https://doi.org/10.5050/KSNVE.2021.31.6.642

축소 기체 구조 모델을 이용한 고속 비행 복합형 무인 회전익기의 능동 진동 제어 시험

홍성부^* ; 박재상^†

Active Vibration Control Test of High-speed Compound Unmanned Rotorcraft Using Scaled Airframe Model

Sung-Boo Hong^* ; Jae-Sang Park^†

*Dept. of Aerospace Eng., Chungnam National University, Graduate Student

Correspondence to: ^†Member, Dept. of Aerospace Eng., Chungnam National University, Associate Professor E-mail : aerotor@cnu.ac.kr ‡ Recommended by Editor Jung Woo Sohn

Abstract

Active vibration control for a 25 %-scale model of a high-speed compound unmanned rotorcraft was experimentally studied. The compound rotorcraft uses wings, propellers, and a lift-offset coaxial rotor system with two blades per rotor. A small-scale airframe structure was manufactured using aluminum and steel and appropriately represents the dynamic similarity of the full-scale model. A ground vibration test (GVT) was used in this experimental work. An active vibration control system (AVCS) using two force generators and three accelerometers was applied for the active vibration control of the small-scale airframe model. Three accelerometers that measure acceleration signals in the vertical direction of the airframe are located at specific airframe locations: the remote cockpit unit, wing root, and wing tip. A 2P rotor hub pitch moment that produces a linear force generator was used to excite the airframe structure. The AVCS using the Fx-LMS algorithm was implemented using MATLAB Simulink, dSPACE ControlDesk, and MicrolabBox. This experimental study shows that the vibration responses of the airframe in the vertical direction at the specific airframe positions are reduced by 47.54 % ~ 84.67 %, and the test results compare reasonably with the simulation results.

Keywords:

Compound Rotorcraft, Active Vibration Control System, Fx-LMS Algorithm, Small-scaled Model

키워드:

복합형 회전익기, 능동 진동 제어 시스템, Fx-LMS 알고리즘, 축소 모델

1. 서 론

최근 회전익기 개발의 선진국에서는 기존의 헬리콥터의 단점인 저속 비행 속도(약 150 knot ~ 170 knot)와 짧은 항속 거리 등의 단점을 해결하고 수직 이착륙 및 제자리 비행 등의 기존 헬리콥터의 장점을 동시에 이용할 수 있는 다양한 형태의 전환형 및 복합형 회전익기의 개발에 집중하고 있다. 복합형 회전익기는 로터, 날개, 및 보조 추력 장치 등을 함께 사용하여 고속 비행을 구현한다. 특히, lift-offset 복합형 회전익기는 lift-offset 로터(강체 동축 반전 로터)⁽¹⁾와 보조 추력 장치를 함께 사용하는 복합형 회전익기이다. Sikorsky 사의 XH-59A, X2 Technology Demonstrator(TD)^(2,3), S-97 Raider, 및 SB > 1는 대표적인 lift-offset 복합형 회전익기(Fig. 1)이며, 우수한 고속 비행 성능을 비행 시험을 통하여 입증하였으나, 동시에 고속 비행 시 극심한 진동을 겪는다는 심각한 문제점이 확인되었다.

Fig. 1

Various lift-offset compound helicopters

회전익기 진동의 다양한 원인 중 메인 로터의 회전에 의해 발생하는 로터 허브 진동이 가장 주요하게 작용한다. 로터 당 블레이드 개수(N_b)의 정수배(n)만큼의 로터 허브의 진동 하중 성분(nN_bP = nN_b/rev)이 기체를 가진한다. 이때 1P(= 1/rev)는 무차원화 된 로터 회전 속도를 의미한다. Lift-offset 로터는 상/하 로터 사이의 간격을 유지하기 위하여 강성이 상당히 큰 블레이드(rigid blade)를 이용하므로 기존 헬리콥터에 비하여 진동이 매우 심대하며, 기체에 전달된 진동은 탑승감 저하, 구조의 피로 수명 단축, 및 유지비용 증가 등의 다양한 문제를 야기하고 lift-offset 복합형 회전익기의 최대 비행 속도를 제한할 수 있다.

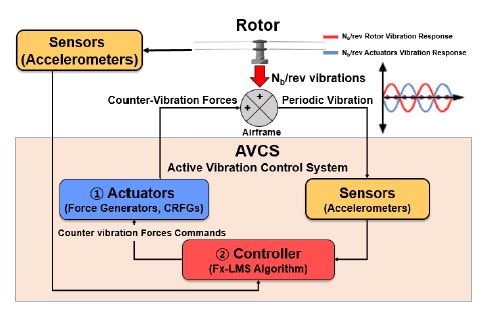
Lift-offset 복합형 회전익기는 고속 비행시 적절히 메인 로터의 회전을 감속시키기^(1~3) 때문에 댐퍼 등의 기존의 수동 진동 제어 기법보다 넓은 주파수 대역 및 비행 환경에 따라 변화되는 진동 특성에서도 적극적으로 적용 가능한 능동 진동 저감 기법의 적용이 필요하다. Sikorsky사는 X2TD^(2,3), S-97 Raider, 및 SB>1 Defiant와 같은 lift-offset 복합 헬리콥터의 기체 진동을 제어하기 위해 다양한 능동 진동 저감 기법 중 능동 진동 제어 시스템(active vibration control system, AVCS)을 사용하였다. AVCS(Fig. 2)는 기체 진동 신호와 진폭은 같고 위상은 반대인 진동 상쇄 신호를 이용하여 기체를 가진하여 기체 진동을 제어하는 기법으로, 진동 상쇄 하중을 생성하는 하중 발생기(force generator), 가속도계(accelerometer), 및 폐루프 피드백 제어기(closed-feedback controller)로 구성된다^(4~7).

Fig. 2

Concept of AVCS

NASA Langley Research Center와 Bell사는 AH-1G(Fig. 3(a)⁽⁸⁾) 및 V-22(Fig. 3(b)^(8,9))의 stick-line 모델의 축소 기체 모델을 이용한 능동 진동 제어의 시험 연구 결과를 바탕으로 V-22 기체에 multipoint adaptive vibration suppression system(MAVSS)로 알려진 고조파 제어(higher harmonic control, HHC) 기법의 적용 가능성을 판단하였다.

Fig. 3

Scaled airframe models

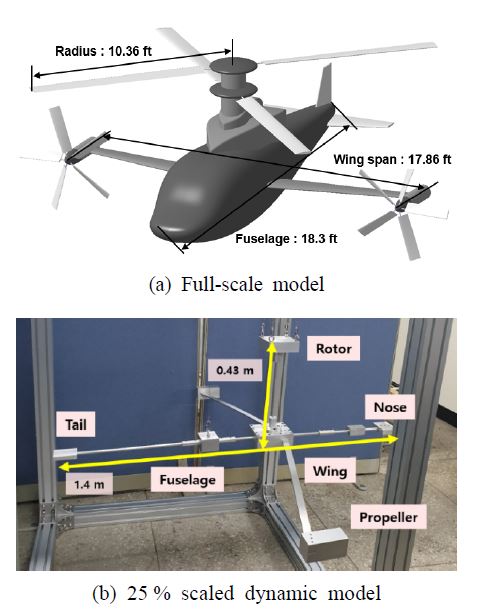
Lift-offset 로터와 한 쌍의 날개 및 프로펠러를 함께 사용하는 복합형 회전익기에 대하여서는 AVCS를 이용하여 동체뿐만 아니라 날개의 진동을 동시에 감소(제어)를 위한 연구가 필요하며 이를 시뮬레이션뿐만 아니라 시험을 통한 시연 연구가 수행되어야 한다. 따라서 이 연구에서는 현재 개념 설계 연구 중인 Lift-offset 동축반전 로터, 날개, 및 프로펠러를 동시에 사용하는 5000 lb급 복합형 회전익기(Fig. 4(a))에 대하여 축소 기체 모델을 설계 및 제작(Fig. 4(b))하고 이에 대한 AVCS 적용의 진동 제어 시뮬레이션 및 시연 연구를 수행한다.

Fig. 4

Unmanned lift-offset compound rotorcraft

이 논문의 25 % 축소 기체 모델은 3차원 설계 프로그램인 CATIA와 유한요소 해석 프로그램인 MSC.NASTRAN을 이용하여 설계하였다. AVCS를 이용한 능동 진동 제어 시험 연구를 위하여서는 3개의 선형 하중 발생기와 3개의 가속도계를 이용하였다. MATLAB Simulink, dSPACE ControlDesk, 및 MicrolabBox를 함께 사용하여 AVCS를 구현하였다. 시험 및 시뮬레이션 연구를 통하여 230 knot에서의 기체 수직 방향의 2P 진동 응답을 적절히 제어할 수 있음을 확인하였다.

2. 본 론

2.1 능동 진동 제어 테스트 벤치 구축

(1) 고속 비행 복합형 무인 회전익기의 25 % 축소 기체 구조 설계 및 제작

선행 연구 결과^(10,11)를 바탕으로 고속 비행 복합형 무인 회전익기 기체 구조의 진동 응답 측정 및 능동 진동 제어를 소규모의 연구실에서 시연하기에 적절할 수 있도록 stick-line 모델 기반의 1.4 m 크기의 축소 기체 구조(25 % 축소 모델, Fig. 4(b))를 설계 및 제작하였다. 축소 기체 구조의 재료로는 가공이 용이한 알루미늄 및 스테인리스 스틸을 이용하였으며, 3차원 설계 프로그램인 CATIA를 사용하여 설계하였다. 이때 상용 유한요소 해석 프로그램인 MSC.NASTRAN을 이용한 축소 기체에 대한 저차 모드 해석 결과가 선행 연구⁽¹⁰⁾의 full-scale 기체의 1차 날개 및 동체 모드 특성을 적절히 구현하도록 축소 기체 구조의 기하학적 형상과 단면적 등을 적절히 설계하였다. 축소 기체 구조 모델에 대한 설계, 모드 특성, 및 기체 진동 응답 시뮬레이션에 대한 자세한 소개는 참고문헌 11번에 주어져 있다.

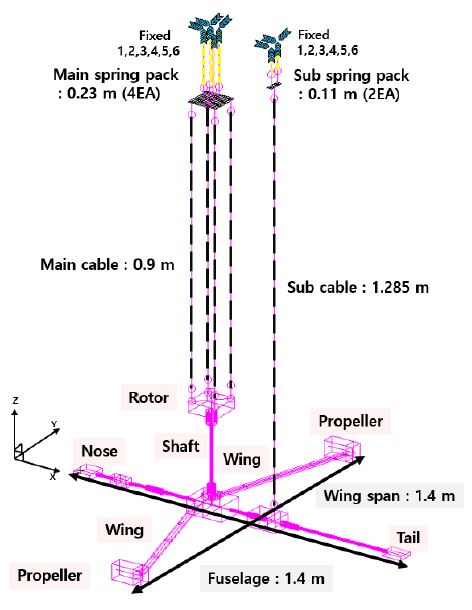
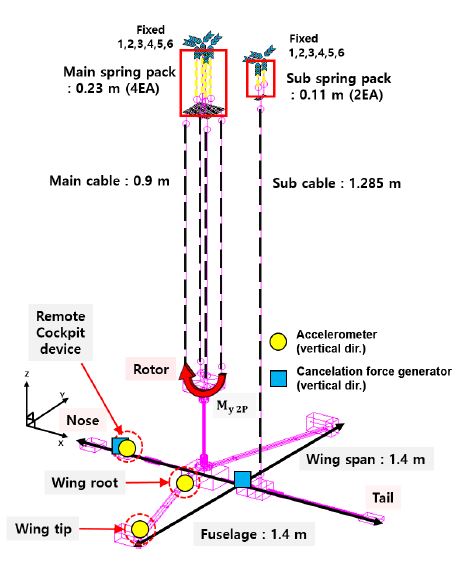
제작된 축소 기체 구조를 이용한 지상 진동 시험(GVT, ground vibration test)의 경계 조건을 자유 경계 조건의 비행 조건과 유사하도록 구현하기 위해 2개의 스프링 팩을 추가하여 축소 기체 구조를 이용한 지상 진동 시험을 구축하였다. 스프링 팩을 구성하는 스프링의 제원은 시제품 물성치를 사용하였으며 스프링과 강철 케이블(diameter = 1Φ)의 길이를 적절히 조절하여 6개의 강체 모드가 적절히 구현되도록 하였다. 이후 지상 진동 시험을 수행하여 제작된 축소 기체 모델이 비행 속도 230 knot의 선행 연구⁽¹⁰⁾의 full-scale모델의 기체 진동 응답을 적절히 구현할 수 있도록 스프링과 케이블의 개수 및 길이 등 최적의 조합을 결정하였다. 최종 설계 및 제작된 축소 기체 구조의 총 중량은 9.2 kg이고, 구축된 능동 진동 제어 시연 연구에 사용된 GVT 구성도는 Fig. 5와 같으며 230 knot 비행 속도에서의 2P 진동수의 값은 15.636 Hz이다.

Fig. 5

GVT model for 25 % scaled unmanned lift-offset compound rotorcraft

(2) 능동 진동 제어 시험 장치의 구성

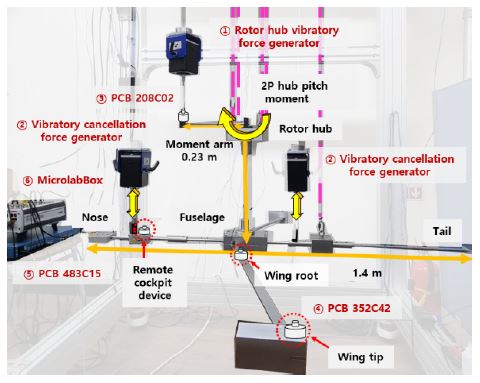
2P 로터 허브 하중 생성을 위하여 1개의 선형 하중 발생기(K2004E01 SmartShaker, Fig. 6의 ①)를 사용하였으며, lift-offset 로터의 2P 허브 하중 중 선행 연구⁽¹²⁾의 연구 결과를 참고하여 중 기체 진동 응답에 지배적인 영향을 보이는 허브 피치 모멘트(M_y2P)만 이용하였다. 2P 허브 피치 모멘트를 선형 하중 발생기로부터 생성하기 위해 강성이 높은 열처리된 강 재질의 모멘트 암을 사용하였다. 이 논문의 lift-offset 복합형 회전익기의 프로펠러는 수평 비행 시 축대칭 유동 조건에서 사용되므로 lift-offset 로터에 비하여 기체 진동의 유발이 매우 적다고 가정하였다.

Fig. 6

Experimental equipment for AVCS test

Stick-line 모델의 특성 상, 기체 축 방향에 대한 선형 하중 발생기의 가진이 쉽지 않으므로 이 시험 연구에서는 기체 수직 방향의 진동 응답 제어만 고려하였다. 기체 수직 방향의 진동 응답을 제어하기 위한 능동 진동 제어 시스템의 진동 상쇄 하중을 생성하는 2개의 선형 하중 발생기(K2004E01 SmartShaker, Fig. 6의 ②)는 각각 다른 위치에 기체 수직 방향으로 배치하여 사용하였다. 이 연구의 능동 진동 제어 시험에 사용된 선형 하중 발생기의 최대(peak-to-peak) 힘은 31 N이다. Remote cockpit device 위치에서 full-scale 모델의 유사한 크기의 진동 응답을 나타낼 수 있도록 로터 허브 진동 하중을 생성하는 선형 하중 발생기는 최대 힘의 90 %로 고정하여 사용하였으며, 진동 상쇄 하중 발생기의 경우, 선행 연구⁽⁴⁾를 참고하여 최대 힘의 60 %로 제한하여 사용하였다.

가진기로부터 축소 기체 구조에 전달되는 하중은 하중 센서(PCB 208C02, Fig. 6의 ③)를 사용하여 측정하였으며, 축소 기체 구조의 기체 주요 위치에서 기체 수직 방향의 진동 응답은 1축 가속도계(PCB 352C42, Fig. 6의 ④)를 사용하여 측정하였다. 신호 변환 및 필터링을 위하여 PCB사의 Model 483C15(Fig. 6의 ⑤)를 사용하였으며, 신호 획득, 연산 및 실시간 제어 신호 출력 장비로 dSPACE사의 MicrolabBox(Fig. 6의 ⑥)를 이용하였다.

2.2 능동 진동 제어 시스템(AVCS)

(1) Fx-LMS 알고리즘

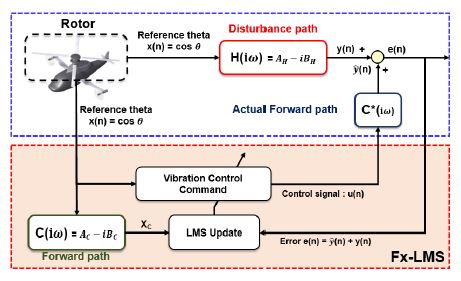
Fig. 7은 축소 기체 구조를 이용한 기체 수직 방향의 능동 진동 제어 시험을 위해 사용된 Fx-LMS 알고리즘 기반의 AVCS의 블록 다이어그램을 나타낸다^(7,10). Disturbance path(H(iω))는 2P 로터 허브 진동 하중으로부터 발생되는 기체 진동의 전달 함수 모델을 의미한다. Actual forward path(C^*(iω))는 진동 상쇄 하중 발생기의 제어 입력(control signal, u(n)))으로부터 발생되어 기체에 전달되는 상쇄 진동의 동특성을 나타내며, forward path(C(iω))는 지상 진동 시험을 통해 얻어진 actual forward path(C^*(iω))의 수학적 전달 함수 모델을 의미한다. Fx-LMS 알고리즘은 가속도계로 측정되는 에러 신호(e(n), 식 (1))가 최소가 되도록 하중 발생기의 제어 입력(u(n))을 지속적으로 업데이트한다. 이후 업데이트 된 제어 입력은 진동 상쇄 하중 발생기로 전달되어 2P 로터 허브 진동 하중에 의한 기체 진동(y(n))과 위상이 반대인 상쇄 진동 응답 ( $y^n$ )을 발생시켜 기체 진동을 제어(감소)한다^(4,5).

e n = y^n + y n = C * u n + y n ≈ C u n + y n

(1)

Fig. 7

Block diagrams for AVCS

Fx-LMS 알고리즘^(4~5)의 제어 입력(u(n))은 매 시간 스텝(time step)마다 경사 하강법(gradient descent⁽⁶⁾)을 이용하여 계산된다. 에러 신호(e(n))를 최소화 하기 위한 목적 함수(J)의 정의와 업데이트된 제어 입력(u(n+1))의 표현은 다음의 식 (2)와 (3)과 같다.

J = E e n 2 = e n H e n

(2)

u n + 1 = u n - 12 μ ∂ J n ∂ u n = u n - μ C H e n

(3)

이때, μ는 LMS 업데이트 방정식(식 (3))에 의해 실시간으로 계산되는 제어 입력의 수렴 속도를 결정하는 파라미터이며, μ의 값은 수렴 속도뿐만 아니라 제어기의 안정성을 결정하기 때문에 적절한 값을 사용하여야 한다. 이 논문에 사용된 AVCS 및 Fx-LMS 알고리즘에 대한 보다 자세한 내용은 선행 연구^(4~7)에 서술되어 있다.

(2) 시스템 식별

AVCS를 구성하는 전달 함수 모델은 선형 시불변 (linear time invariant, LTI) 시스템으로, 이때, 시스템 식별(system identification)은 이미 알고 있는 입력값과 측정을 통해 확인 가능한 출력값을 이용하여 미지의 전달 함수 모델을 얻어내는 과정을 의미한다. 이 연구에서는 2P 로터 회전 진동수의 로터 허브 하중과 진동 상쇄 하중을 사용하여 기체를 각각 가진하여 지상 진동 시험을 수행하고 기체 주요 위치에서 측정된 진동 응답을 이용하여 기체 동역학 모델 및 작동기 모델에 대한 각각의 전달 함수를 얻었다. 측정된 진동 응답의 2P 진동수 성분을 추출하기 위해 MATLAB curve fitting tool를 이용하여 푸리에 변환(fourier transform)을 수행하였다.

2P 로터 허브 진동 하중에 의한 기체 진동을 의미하는 disturbance path(H(iω))의 시스템 식별 과정은 아래 Fig. 8과 같다. 입력값인 reference signal(x(n))는 로터의 2p 신호의 위상을 나타내며, reference signal(x(n))의 θ(n)은 로터당 2개의 블레이드를 갖는 lift-offset 로터의 매 시간 스탭의 회전을 적절히 표현할 수 있도록 식 (4)와 같이 정의한다. 이때는 로터의 회전속도를 표현한다. 출력값은 가속도계를 통해 측정된 기체 주요 위치에서 2P 기체 진동 응답(y(n))이다.

θ n = N b × ω × t n

(4)

Fig. 8

System identification of disturbance path

제어 입력(u(n))으로부터 하중 발생기가 생성하는 기체 진동의 수학적 전달 함수인 actual forward path(C^*(iω))는 가진진동수와 진동 상쇄 하중의 크기에 따라 다르게 표현될 수 있다. 따라서 실시간으로 업데이트되는 제어 입력으로 인하여 변화하는 진동 상쇄 신호의 동특성을 적절히 표현하기 위해, 진동 상쇄 하중 발생기의 최대 힘의 0 % ~ 60 % 이내로 다양한 크기의 진동 상쇄 하중을 이용하여 기체를 가진하여 시스템 식별을 수행한다. 업데이트된 제어 입력으로부터 생성된 상쇄 진동 하중의 진동수는 유지된 채로 진폭와 위상만 적절히 변화시킬 수 있도록 하중 발생기의 제어 입력은 Cosine과 Sine 성분의 합인 조화 함수의 형태로 식 (5)와 같이 정의하였다.

u n = A cos ⁡ θ n + B sin ⁡ θ n

(5)

제어 입력에 따른 진동 상쇄 하중에 의한 2P 기체진동 응답 ( $y^n$ )은 식 (6)과 같이 표현 가능하다. 이때 A₂ 및 B₂는 MATLAB curve fitting tool을 이용하여 추출한 기체 주요 위치에서 2P 진동 응답의 1차 항의 상수이다.

y^n = C * u n = A A C * cos ⁡ θ n + B C * sin ⁡ θ n + B A C * sin ⁡ θ n - B C * cos ⁡ θ n

(6)

따라서 actual forward path(C^*(iω))의 전달 함수 모델은 식 (7)로 정리하여 나타낼 수 있으며, Fig. 9와 같이 표현된다.

C * i ω = A C * - i B C * A C * = A A 2 + B B 2 A 2 + B 2, B C * = A B 2 - B A 2 A 2 + B 2

(7)

Fig. 9

System identification of actual forward path

2.3 축소 기체 구조를 이용한 능동 진동 제어 시험 기법

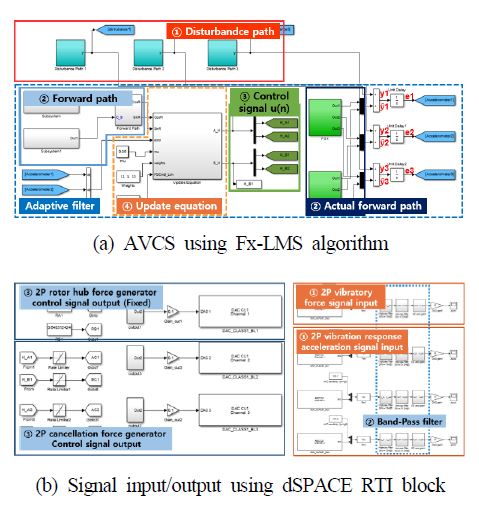
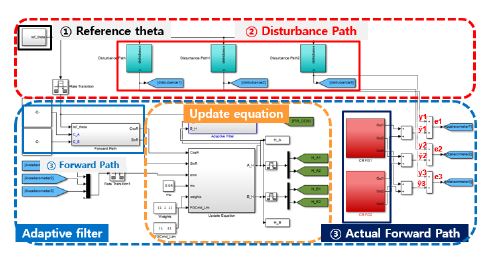
이 저자들의 선행 연구의^(10,11,13) 능동 진동 제어 시뮬레이션 프레임워크를 기반으로 MATLAB Simulink 환경에서 Simulink 블록과 dSPACE RTI(real-time interface) 블록을 사용하여 능동 진동 제어 시험에서 사용될 능동 진동 제어 알고리즘을 모델링하였다(Fig. 10). 축소 기체를 이용한 능동 진동 제어 시험에 사용된 하중 발생기의 가진진동수는 고속 비행 복합형 무인 회전익기의 2P 기체 진동 응답의 진동수를 표현하기 위하여 2P 진동수로 고정하였다. AVCS를 구성하는 disturbance path(Fig. 10(a)의 ①)와 actual forward path 및 forward path(Fig. 10(a)의 ②)의 전달 함수는 전술한 시스템 식별 과정을 통하여 얻었으며, 진동 상쇄 하중 발생기로 전달되는 제어 입력(Fig. 10(a)의 ③)은 전술한 LMS 업데이트 방정식(식 (3), Fig. 10(a)의 ④)을 이용하여 매시간 스탭(0.0001 s)마다 계산된다. 이때 선행 연구의⁽¹⁰⁾ 시뮬레이션 결과인 비행 속도 230 knot 에서의 고속 수평 비행 조건을 구현하기 위한 2P 로터 허브 진동 하중의 생성을 위한 하중 발생기의 제어 입력은 업데이트 되지 않고 고정된 값을 사용한다.

Fig. 10

MATLAB simulink block diagram for AVCS test

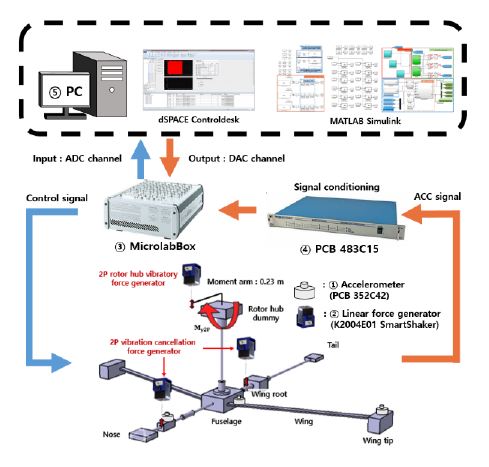
Fig. 11은 AVCS를 이용한 능동 진동 제어 시험의 개략도를 나타낸다. 이 논문의 AVCS는 3개의 가속도계(Fig. 11의 ①)와 2개의 진동 상쇄 하중 발생기 (Fig. 11의 ②)를 사용하여 구성되었다. 가속도계의 위치는 선행 연구⁽¹⁰⁾의 가속도계의 배치를 참고하여 remote cockpit device, wing root 및 wing tip에 기체 수직 방향으로 배치하였다. 2개의 진동 상쇄 하중 발생기의 위치는 stick-line 모델 기반의 축소 기체 구조의 형상 특성을 고려하고, 축소 기체 구조의 진동 상쇄 하중 발생기를 이용한 시스템 식별 결과를 바탕으로 적절히 결정하였다.

Fig. 11

Schematic diagram for active vibration control test using a small-scaled airframe model

축소 기체 구조의 주요 위치에 부착된 가속도계 (Fig. 11의 ①)의 신호는 MicrolabBox(Fig. 11의 ③)의 ADC 채널(Fig. 10(b)의 ①) 에 입력되며, 가속도계의 신호 수집 시 신호 처리 및 노이즈 필터링을 위하여 PCB사의 model 483C15(Fig. 11의 ④)와 high-pass filter와 low-pass filter를 결합한 band-pass filter(Fig. 10(b)의 ②)를 사용하였다. 2P 로터 허브 하중 및 진동 상쇄 하중을 생성하는 선형 하중 발생기를 구동하기 위한 제어 입력은 MicrolabBox의 DAC 채널 (Fig. 10(b)의 ③)로 출력된다. MATLAB Simulink 블록과 dSPACE RTI 블록을 사용하여 모델링 된 능동 진동 제어 알고리즘 모델은 PC(Fig. 11의 ⑤)의 dSPACE ControlDesk 프로그램에 연동되어 이 연구의 능동 진동 제어 시험을 전체적으로 제어한다.

2.4 축소 기체 구조의 유한요소 모델을 이용한 능동 진동 제어 시뮬레이션 기법

2.1절에 서술된 축소 기체를 이용한 능동 진동 제어 시험 연구 모델에 대하여 시뮬레이션 연구를 수행하기 위하여 Fig. 12의 해석 모델을 이용하였다. 그림의 해석 모델은 MSC.NASTRAN을 이용한 유한요소 모델로 구축되었다. 자세한 모델링 기법 및 축소 기체 모델의 동특성 해석 결과에 대한 서술은 참고문헌⁽¹¹⁾에 주어져 있으나, 다음과 같이 간단히 정리할 수 있다. 축소 기체 구조의 유한요소 모델링 시, 51개의 1D Bar 요소와 211개의 2D Shell 요소를 사용하였다. 번지 케이블과 스프링은 CBAR와 CBUSH 요소를 각각 이용하여 구현하였으며, 시험 연구 모델과 동일하게 6개의 강체 모드를 적절하게 표현할 수 있도록 모델링하였다. 2P 로터 허브 진동 하중의 생성을 위한 하중 발생기와 진동 상쇄 하중의 하중 발생기 역시 자유 경계 조건을 이용하여 구현 되었으므로 이 유한요소 모델링에서는 표현되지 않았다. 가속도계의 무게(0.0028 kg)는 축소 기체 구조의 전체 무게(9.2 kg)에 비하여 상당히 작은 값이므로 모델링하지 않았다. 유한요소 모델링 후, 주파수 응답 해석을 수행하여 이로부터 얻은 기체의 고유진동수가 자유 경계 조건의 모드 해석의 고유진동수와 유사함을 확인하였다^(10,11).

Fig. 12

Finite element model of a small-scaled airframe model for active vibration control simulation

이후 고속 비행 복합형 무인 회전익기의 축소 기체 구조의 유한요소 모델을 이용한 능동 진동 제어 시뮬레이션을 위해 MATLAB Simulink를 사용하여 MIMO 기반의 AVCS를 Fig. 13과 같이 모델링하였다. Reference theta(Fig. 13의 block ①)는 축소 기체 구조의 2P 허브 하중의 위상을 나타내며, disturbance path(Fig. 13의 Block ②)는 유한요소 모델의 2P 진동 응답 해석 결과의 전달 함수를 의미한다. Forward path 및 actual forward path(Fig. 14의 block ③)는 진동 상쇄 하중 발생기를 통해 생성되는 유한요소 모델로 표현된 기체 진동의 전달 함수를 나타내며, 하중 발생기의 기체 수직 방향의 하중은 운용 범위 내의 최대 힘(maximum force의 60 %)을 가진하여 전달함수 모델을 추출하였다. AVCS의 제어 입력을 계산하기 위해 능동 진동 제어 시험에 사용한 Fx-LMS 기법을 동일하게 사용하였으며, 에러 신호(e(n))를 최소로 만드는 최적의 제어 입력 신호(u(n)) 역시 시험 연구에서 사용된 LMS 업데이트 방정식(식 (3))을 이용하여 계산하였다.

Fig. 13

MATLAB simulink block diagram for active vibration control simulation

Fig. 14

Comparison of 2P vertical vibration responses between full- and small-scale models (230 knot)

2.5 연구 결과

(1) 지상 진동 시험

능동 진동 제어 시험을 위해 먼저 disturbance path (H(iω)) 및 actual forward path(C^*(iω))의 시스템 식별을 수행한다. 선행 연구의⁽¹⁰⁾ 비행 조건 230 knot에서의 고속 비행 복합형 무인 회전익기의 기체 진동 응답 해석 결과와 유사한 수준의 기체 수직 방향의 2P 진동 응답을 축소 기체 모델에서도 얻을 수 있도록 2P 허브 피치 모멘트의 크기를 Fig. 12의 MSC.NASTRAN 모델을 이용한 시뮬레이션을 통하여 결정하였다. 가속도계로 측정된 기체 수직 방향의 2P 기체 진동 응답은 MATLAB curve fitting tool을 이용하여 주파수 영역으로 변환하고 전술한 시스템 식별 과정을 통해 25 % 축소 기체 구조의 기체 수직 방향 2P 진동 응답의 동특성(disturbance path, H(iω))을 추출한다. 이후 2개의 진동 상쇄 하중 발생기를 각각 작동하여 작동기의 운용 범위 이내의 진동 상쇄 하중을 기체 구조 모델에 가한 후 측정된 가속도 신호를 분석하여 진동 상쇄 하중 발생기의 전달 함수 모델(actual forward path, C^*(iω)))을 식별하였다.

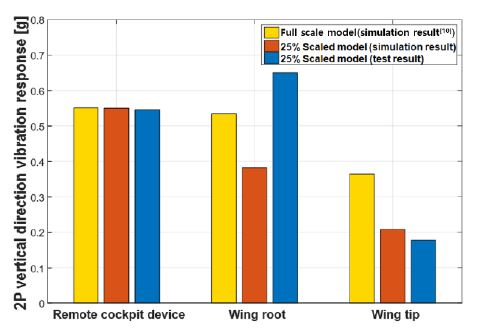
Fig. 14는 선행 연구⁽¹⁰⁾의 full-scale 모델을 이용한 GVT 모델의 기체 수직 방향의 2P 진동 응답 해석 결과와 이 논문의 축소 기체 구조를 이용한 GVT 모델의 기체 수직 방향의 2P 기체 진동 응답 해석 및 지상 진동 시험 결과를 비교하여 나타낸다. 선행 연구⁽¹⁰⁾의 full-scale 모델의 기체 진동 응답 해석에서는 3종류의 2P 로터 허브 진동 하중(F_x2p, F_z2p, 및 M_y2P)이 모두 이용된 반면, 이 연구의 축소 기체 모델의 경우, 2P 허브 피치 모멘트(M_y2P)만 사용하였다. 축소 기체 구조를 이용한 지상 진동 시험을 수행한 결과, 축소 기체 구조의 주요 위치(remote cockpit device, wing root 및 wing tip)에서 기체 수직 방향의 2P 기체 진동 응답이 선행 연구의⁽¹⁰⁾ full-scale 모델의 시뮬레이션 연구 결과와 비교하여 1.07 % ~ 51.27 %의 차이를 보였다. Remote cockpit device의 위치에서는 매우 작은 오차(－1.07 %)를 가지므로, 축소 기체 모델은 full-scale 모델의 2P 기체 진동 응답이 가장 극심한 remote cockpit device의 기체 진동 응답의 크기를 잘 모사하고 있다. 그러나, wing tip의 위치에서는 －51.27 %의 비교적 큰 오차가 확인되었다. Fig. 14의 평균 오차의 크기(24.74 %)는 선행연구^(8,14,15)의 평균 오차(15.46 %)의 크기와 비교 시, 다소 높으나, 이 연구의 모델의 경우 선행 연구에 비하여 상당히 고속 비행(230 knot) 조건임을 고려할 시, 얻어진 오차의 크기는 적합하다고 판단된다. 또한, 축소 기체 구조 모델의 wing tip에서 기체 진동 응답이 full-scale 모델 대비, 다소 낮게 예측 및 측정되었으나, 일반 헬리콥터 진동 목표⁽¹⁶⁾ 수준인 0.1 g 이상의 높은 진동을 보이므로 AVCS 적용 가능성을 평가하기 위한 적절한 지상 진동 시험 모델을 구축하였다고 판단하였다.

(2) AVCS를 이용한 능동 진동 제어

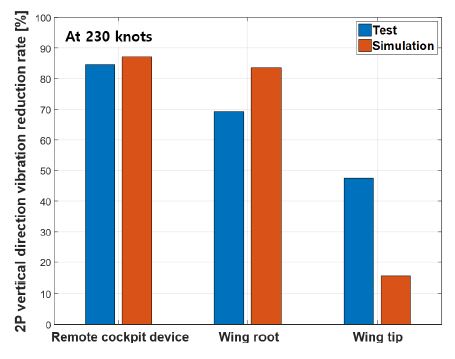
전술한 축소 기체 구조 모델과 AVCS를 이용하여 능동 진동 제어 시험 및 능동 진동 제어의 경향성 평가를 위한 시뮬레이션 연구를 수행하였다. 1축 가속도계를 이용한 축소 기체 구조의 수직 방향의 가속도계 신호는 30초간 수집되었으며, AVCS는 능동 진동 제어 시험 및 시뮬레이션 시작 6초 이후 19초 동안 적용하였다. 능동 진동 제어 시험 시작 15초 ~ 25초에 수집된 2P 기체 진동 응답의 피크의 절대값의 평균을 이용하여 능동 진동 제어 성능을 평가하였다. Fig. 15는 AVCS를 이용하여 제어(감소)된 기체 수직 방향의 진동 응답의 감소율을 나타내며, 시험의 경우 84.67 % ~ 47.54 %, 시뮬레이션의 결과에서는 87.12 %~15.44 %만큼의 진동 감소율을 얻을 수 있었다.

Fig. 15

2P airframe vibration reductions using AVCS

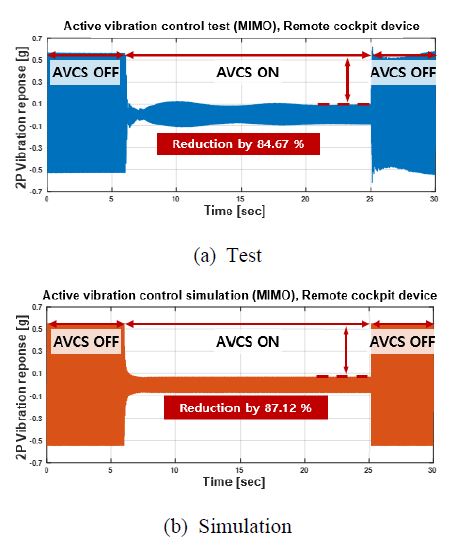
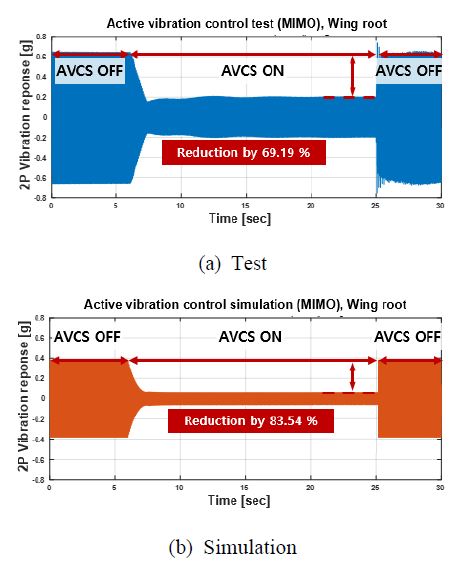
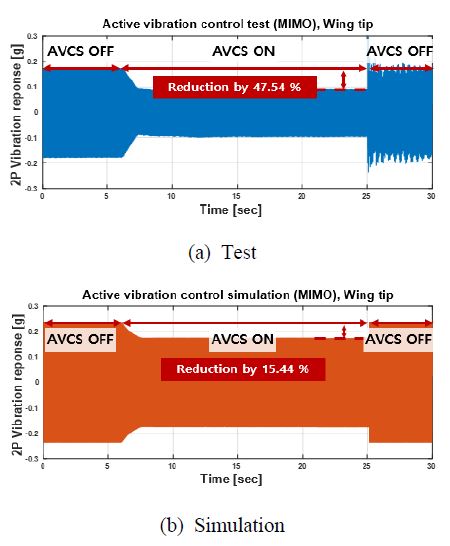
Figs. 16 ~ 18에 축소 기체 모델에 대한 능동 진동 제어의 시험 및 시뮬레이션 연구 결과를 시간 영역에서 나타내었다. Remote cockpit device 위치에서의 시험 및 시뮬레이션 결과가 각각 84.67 % 및 87.12 %의 우수한 감소율을 보이며(Fig. 16), 시험 및 시뮬레이션의 결과의 오차가 2.89 %로 상당히 유사함을 알 수 있다. Fig. 17에 주어진 wing root에서는 69.19 % 및 83.54 %의 진동 감소율을 시험 및 시뮬레이션에서 각각 얻었으며, 역시 우수한 진동 성능을 확인할 수 있다. 마지막으로 wing tip의 진동 응답은 시험 및 시뮬레이션에서 47.54 % 및 15.44 %만큼 각각 감소되었으며(Fig. 18), 이 연구에서 사용된 3곳의 진동 응답 제어 결과 중 가장 낮은 감소율을 보였다. Wing root 및 tip에서의 진동 감소율에 대한 시험 대비 시뮬레이션의 오차는 각각 20.74 % 및 67.52 %로 작은 오차는 아니지만, AVCS를 이용한 선행연구⁽⁴⁾의 진동 감소율에 대한 시험 대비 시뮬레이션의 오차(약 68 %)와 비교 시, 이 연구의 경우, 적절한 수준의 오차로 판단할 수 있다.

Fig. 16

Reduced 2P vertical direction vibration responses using AVCS at remote cockpit device

Fig. 17

Reduced 2P vertical direction vibration responses using AVCS at wing root

Fig. 18

Reduced 2P vertical direction vibration responses using AVCS at wing tip

이와 같은 진동 감소율에 대한 얻어진 오차는 축소 기체 구조의 진동 응답 해석 및 시험의 측정 결과의 차이로 인하여 발생되었으며, 축소 기체 구조에 사용된 재료 물성치와 축소 기체 구조 및 선형 하중 발생기의 자유 경계 조건 구현을 위해 사용된 스프링의 감쇠 효과를 시뮬레이션에서 적절하게 표현하지 못하였기 때문으로 판단된다. 또한 Fig. 16(a)에서 관찰되는 remote cockpit device 위치에서 AVCS작동 시 능동 진동 제어 시험 초기의 진폭의 출렁임은 자유 경계 조건 및 full-scale 모델의 동특성을 적절히 구현하기 위해 낮은 강성의 스프링을 사용하였기 때문으로 사료된다. 그러나 능동 진동 제어 시험과 시뮬레이션 모두 AVCS 작동 이후 능동 진동 제어를 위한 제어 입력이 2초 이내로 수렴되어 매우 유사한 거동을 보였다.

능동 진동 제어 시험 결과, wing root에서 기체 수직 방향의 제어된 2P 기체 진동 응답이 0.201 g로 일반 헬리콥터의 기체 진동 목표⁽¹⁶⁾ 수준인 0.1 g보다 높게 측정되었다(Fig. 17(a)). 그러나 AVCS 적용 이전의 기체 진동 응답(0.6508 g)에 비해 약 70 % 감소한 결과로 매우 높은 수준의 진동 감소율을 보였다. 또한 wing tip에서 AVCS를 이용한 능동 진동 제어 시험 결과 AVCS 작동 이전의 기체 진동 응답은 0.177 g로 0.1 g 이상의 높은 진동 응답이 측정되었으나, AVCS 작동 이후 0.0843 g로 제어(감소)되어 일반 헬리콥터 진동 목표 수준인 0.1 g이하의 진동 수준을 보이기 때문에 이 논문의 AVCS를 이용한 능동 진동 제어 시험 결과는 적절한 것으로 판단하였다. 따라서 이 연구의 lift-offset 복합형 회전익기의 동체에 AVCS를 적용하여 동체뿐만 아니라 날개 및 프로펠러 위치에서도 적절한 능동 진동 제어가 가능함을 확인하였다.

3. 결 론

이 연구에서는 lift-offset 로터, 날개 및 프로펠러를 사용하는 5000 lb급의 고속 비행 복합형 무인 회전익기에 대하여 축소 기체 구조를 이용한 기체의 능동 진동 진동 제어 시험 연구를 수행하였다. 축소 기체 구조는 실물 크기 모델의 230 knot 조건의 기체 진동 응답을 적절히 모사하며, 1.4 m 크기 (25 % small-scale model)로 설계 되었으며, 비행 조건을 모사할 수 있도록 지상 진동 시험 모델로 구현되었다.

기체 수직 방향의 2P 기체 진동 응답에 대하여 능동 진동 제어 시험을 위해 3개의 가속도계와 2개의 하중발생기로 구성된 MIMO 기반의 AVCS를 사용하였다. AVCS의 진동 상쇄 하중을 생성하는 제어 입력을 Fx-LMS 알고리즘에 의해 결정하였으며, 선행 연구의 능동 진동 제어 시뮬레이션 프레임워크를 기반으로 MATLAB Simulink 환경에서 AVCS를 구성하였다. MATLAB Simulink 블록과 dSPACE RTI 블록을 사용하여 구현된 능동 진동 제어 알고리즘 모델은 PC의 dSPACE ControlDesk 프로그램에 연동되어 이 연구의 능동 진동 제어 시험을 전체적으로 제어하였다.

축소 기체 구조에 AVCS를 적용하였을 경우, 대부분의 기체 주요 위치에서 기체 수직 방향의 2P 진동이 84.67 % ~ 47.54 % 감소함을 확인하였다. 축소 기체 구조의 Remote cockpit device 위치에서 시험-시뮬레이션의 진동 감소율이 매우 잘 일치(2.89 %의 오차)하였으며, 능동 진동 제어 시험과 시뮬레이션 모두 AVCS 작동 이후 능동 진동 제어를 위한 제어 입력이 2초 이내로 수렴되어 매우 유사한 거동을 보였다. 특히 wing tip에서 기체 진동 응답이 일반적인 헬리콥터의 진동 목표 값인 0.1 g 이하로 제어되었다. 이 연구를 통하여 lift-offset 복합형 회전익기에 AVCS를 사용하여 동체에서 생성된 진동 상쇄 하중으로부터 동체뿐만 아니라 날개 및 프로펠러 위치에서도 기체 진동 응답 제어가 가능함을 축소 기체 구조 모델을 이용한 시험 및 시뮬레이션을 통하여 확인하였다.

Acknowledgments

이 연구는 국방과학연구소의 지원으로 차세대 고속 복합형 무인 회전익기 특화연구실에서 수행되었습니다. 이 연구는 2020년도 정부 (교육부)의 재원으로 한국연구재단의 기초연구사업의 지원을 받아 수행되었습니다(2020 R1I1A3071793). 이 논문은 2021년도 정부 (과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구입니다(2021 R1A5A1031868).

References

Ruddell, A. J., Groth, W. and McCutcheon, R., 1981, Advancing Blade Concept(ABC) Technology Demonstrator, US Army Research and Technology Laboratories, USAAVRADCOM-TR-81-D-5.
Bagai, A., 2008, Aerodynamic Design of the X2 Technology DemonstratorTM Main Rotor Blades, Proceedings of American Helicopter Society 64th Annual Forum, Montréal, Canada.
Blackwell, R. and Millott, T., 2008, Dynamics Design Characteristics of the Sikorsky X2 TechnologyTM Demonstrator Aircraft, Proceedings of American Helicopter Society 64th Annual Forum, Montréal, Canada.
Kim, D.-H., Kim, T.-J., Jung, S.-U. and Kwak, D.-I., 2016, Test and Simulation of an Active Vibration Control System for Helicopter Applications, International Journal of Aeronautical and Space Sciences, Vol. 17, No. 3, pp. 442~453. [https://doi.org/10.5139/IJASS.2016.17.3.442]
Kim, D.-H., Kwak, D.-I. and Song, Q., 2019, Demonstration of Active Vibration Control System on a Korean Utility Helicopter, International Journal of Aeronautical and Space Sciences, Vol. 20, No. 1, pp. 249~259. [https://doi.org/10.1007/s42405-018-0106-3]
Kim, D.-H., 2021, Multicyclic Helicopter Vibration Control, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 3, pp. 247~259. [https://doi.org/10.5050/KSNVE.2021.31.3.247]
Lee, Y.-L., Kim, D.-H., Park, J.-S. and Hong, S.-B., 2020, Vibration Reduction Simulations for Rotor and Airframe of a Lift-offset Compound Helicopter Using Two Active Vibration Control Techniques, Journal of the Aerospace Science and Technology, Vol. 106, 106181. [https://doi.org/10.1016/j.ast.2020.106181]
Kvaternik, R. G., Juang, J.-N. and Bennett, R. L., 2000, Exploratory Studies in Generalized Predictive Control for Active Aeroelastic Control of Tiltrotor Aircraft, NASA/TM-2000-210552.
Piatak, D. J. and Kunz, D. L., 1999, Experimental Investigation of a Fullspan Tiltrotor Model with Higher-Harmonic Vibration Control, Proceedings of the Eighth ARO Workshop on Aeroelasticity of Rotorcraft Systems, State College, PA.
Hong, S.-B., Lee, Y.-L. and Park, J.-S., 2020, Airframe Vibration Reduction Simulations of High-speed Compound Unmanned Rotorcrafts Using Active Controls, 2020 Spring Conference of the Korean Society of Aeronautics and Space Sciences Proceedings, Sokcho, Korea.
Hong, S.-B., Kim, J.-S. and Park, J.-S., 2020, Design and Active Vibration Control Simulation for a Small-scaled Model of High-speed Compound Unmanned Rotorcrafts, 2020 Korea Institute of Science and Technology Annual Conference Proceedings, Online, Korea.
Kim, J.-S., Hong, S.-B., Kwon, Y.-M. and Park, J.-S., 2021, Effect of Lift-offset Rotor Hub Vibratory Load Components on Airframe Vibration Responses of High-speed Compound Unmanned Rotorcrafts, Journal of the Korea Institute of Military Science and Technology, Vol. 24, No. 3, pp. 255~263. [https://doi.org/10.9766/KIMST.2021.24.3.255]
Hong, S.-B., Kwon, Y.-M., Kim, J.-S. et al., 2021, Active Airframe Vibration Control Simulations of Lift-offset Compound Helicopters in High-speed Flights, Journal of the Korea Institute of Military Science and Technology, Vol. 24, No. 4, pp. 357~367. [https://doi.org/10.9766/KIMST.2021.24.4.357]
Settle, T. and Nixon, M., 1997, MAVSS Control of an Active Flaperon for Tiltrotor Vibration Reduction, Proceedings of the American Helicopter Society 53rd Annual Forum, Virginia, USA.
Yeo, H. and Chopra, I., 2001, Coupled Rotor/Fuselage Vibration Analysis Using Detailed 3-D Airframe Models, Mathematical and Computer Modelling, Vol. 33, No. 10~11, pp. 1035~1054. [https://doi.org/10.1016/S0895-7177(00)00299-5]
Walsh, D., Weiner, S., Arifian, K. et al., 2011, High Airspeed Testing of the Sikorsky X2 TechnologyTM Demonstrator, Proceedings of the American Helicopter Society 67th Annual Forum, Virginia Beach, VA.

Sung-Boo Hong is currently a graduate student in Department of Aerospace Engineering from Chungnam National University, Daejeon, Korea. His research interests include the active vibration control tests and simulations of rotorcraft.

Jae-Sang Park received Ph.D. degree in Mechanical and Aerospace engineering, from Seoul National University, Seoul, Korea in 2006. Dr. Park is currently an associate professor, Department of Aerospace engineering, Chungnam National University, Daejeon, Korea. His research interests include aerospace structural analyses and rotorcraft aeromechanics analyses.