측정 위치에 대한 강건성을 가지는 구조 진동 신호 기반의 결함 있는 복합재 구조물의 분류

1. 서 론

적층 복합재 구조물은 질량 대비 높은 강도를 갖고 있어, 경량화와 고강도화가 동시에 요구되는 시스템에 활용하는 것이 적합하다. 최근 적층 복합재 구조물은 항공기와 풍력 발전기의 블레이드 등 활용 분야를 확장하고 있으며, 가까운 미래에는 전기자동차의 차체 재료로도 활용될 것으로 기대되고 있다. 그러나 적층 복합재 구조물은 복잡한 파괴 특성을 가지고 있어 구조물의 주 재료로 활용되기에는 제한이 있다. 적층 복합재 구조물의 여러가지 파괴 모드 중에서 적층된 층 사이의 결합이 손상되는 층간 분리 현상은 가장 많이 발생하는 결함이다. 층간 분리 현상이 발생하게 되면 구조물의 강성이 크게 저하되고 이에 따라 구조물 전체의 동적 특성이 변하게 된다. 강성이 저하되면 구조물의 고유진동수가 감소하게 되고, 감소된 고유진동수가 구조물의 작동 주파수 또는 가진 주파수와 가까워지게 되면 시스템의 파괴도 발생할 수 있으므로, 적층 복합재 구조물에 발생한 결함은 반드시 탐지되어야 한다.

적층 복합재 구조물에 발생하는 층간 분리를 모델링하기 위한 연구가 다양하게 수행되었다. Saravanos 등은⁽¹⁾ 층간 분리가 구조물의 동적 변화에 미치는 영향을 이론 해석과 실험을 통하여 확인하였다. Cho와 Kim은⁽²⁾ 층간 분리가 발생한 구조물의 거동을 지그재그 변위장 이론을 바탕으로 설명하였다. Radu와 Chattopadhyay는⁽³⁾ 층간 분리가 있는 복합재 구조물의 동적 안정성을 고차 이론을 이용하여 해석하였다. Kim 등은⁽⁴⁾ 압전 재료가 포함된 스마트 복합재에 대하여 층간 분리에 의한 동적 특성 변화를 고찰하였다. 비파괴검사 등 다양한 방법을 통해 복합재 구조물 내부의 결함을 탐지하고자 하는 연구도 다양하게 진행되고 있다. Chattopadhyay 등은⁽⁵⁾ 항공기 구조물의 구조 건정성 모니터링과 결함 예측을 위한 다학제 접근법을 제안하였다. Swan 등은⁽⁶⁾ 복합재 구조물의 층간 분리를 탐지하기 위한 압전 센서의 최적 위치 선정에 대한 연구를 제안하였다. Hong 등은⁽⁷⁾ 복합재 구조물에 발생하는 충격 위치를 검출하고 충격에 의하여 구조물에 손상이 발생하였는지 판단하는 기법을 제안하였다. Han 등은⁽⁸⁾ 레이저 스캐닝과 정상파를 이용하여 평판 구조물의 결함을 탐지하는 기법을 제안하고 성능을 검증하였다. Cho 등은^(9,10) 유도 탄성파를 이미지로 변환하고 이미지를 기반으로 손상 위치를 탐지하거나, 손상 크기를 예측하는 기법을 제안하였다. 또한 초음파 등을 이용한 다양한 비파괴검사 기법들이 제안되었지만, 대부분 주파수 성분 차이가 크게 발생하는 수 kHz 이상의 고주파수 대역의 진동 신호를 이용하고 있으며, 진동 신호의 측정 위치가 변하게 되면 성능이 제한되는 단점이 있다. 또한 연속적으로, 실시간으로 결함을 탐지하는 것은 아직 어려움이 있다⁽¹¹⁾. 최근 Khan 등은⁽¹²⁾ 합성곱 신경망을 이용하여 적층 복합재의 12가지 결함을 분류하는 기법을 제안하였다.

이 연구에서는 1000 Hz 이하 저주파수 대역에서의 구조물의 진동 신호 실험 데이터를 이용하여 복합재 구조물의 결함 유무를 판단하고 결함의 위치를 분류할 수 있는 기법을 제안하고, 제안된 방법의 정확성을 검증한다. 결함이 없는 복합재 보와 결함을 인위적으로 생성한 두 가지 다른 복합재 보를 제작한 후, 고정-자유 경계조건에서 랜덤 가진을 인가하는 진동 실험을 수행하여 구조물의 진동 신호 데이터를 획득한다. 학습 데이터와 테스트 데이터로 사용될 진동 신호의 측정 위치를 달리하여 측정 위치가 다르더라도 강건하게 결함을 탐지할 수 있는지 확인한다. 측정된 진동 신호를 단시간 푸리에 변환을 통하여 이미지로 변환하고 학습과 테스트의 입력 데이터로 이용한다. 먼저 결함 유무를 탐지하기 위하여 오토인코더를 이용한다. 결함이 없는 보의 진동 데이터를 이용하여 오토인코더를 학습하고 모델을 구성한다. 학습된 오토인코더 모델에 결함이 없는 보의 진동 데이터와 결함이 있는 보의 진동 데이터를 입력하고 출력되는 데이터와 입력 데이터의 차이를 비교하여 결함 유무를 탐지한다. 두 번째는 합성곱 신경망 모델을 이용하여 결함이 없는 보의 진동 데이터와 결함의 위치가 다른 두 가지 보의 진동 데이터를 분류한다. 제안된 기법을 통하여 효과적으로 복합재 구조물의 결함을 탐지하고, 서로 다른 위치의 결함들을 구분할 수 있음을 확인한다.

2. 데이터 획득

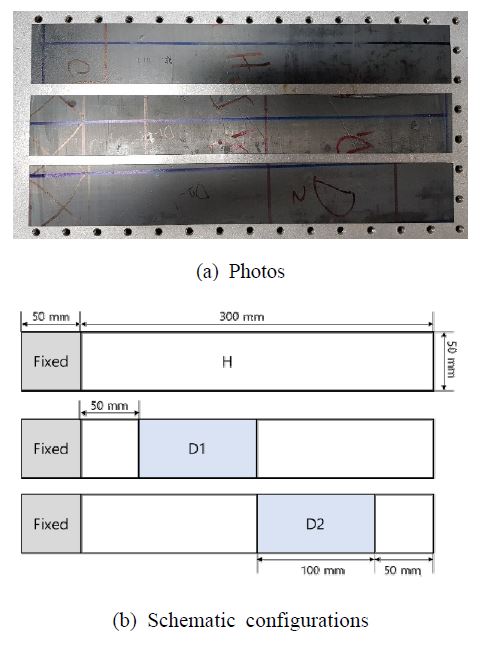
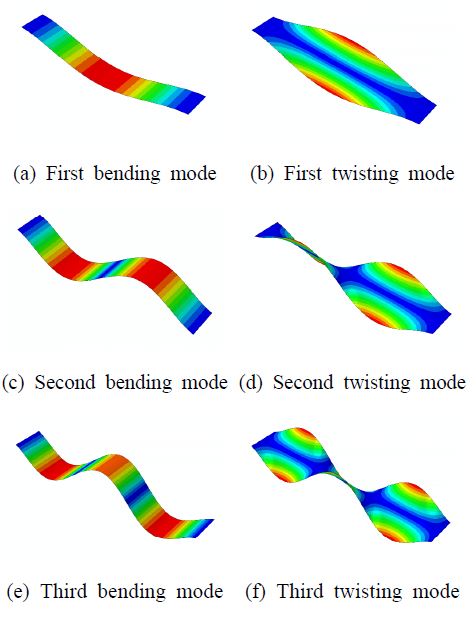
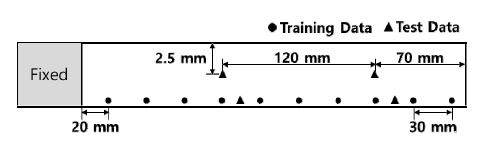
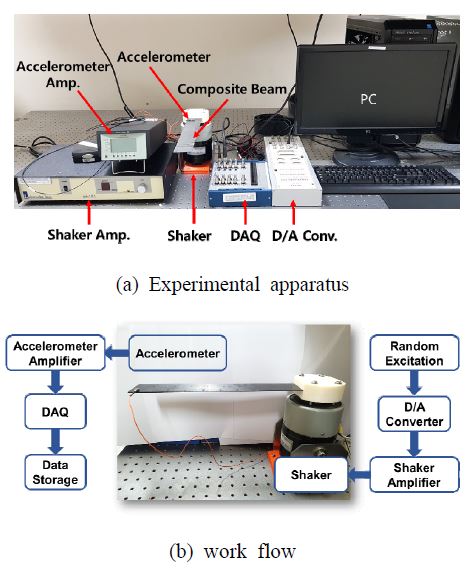
결함이 없는 복합재 시편과 위치가 서로 다른 층간 분리 결함이 있는 두 개의 복합재 시편을 탄소 섬유를 사용하여 제작하였다. 시편은 총 여덟 층을 적층하였고, 가운데를 기준으로 위 아래 네 개의 층을 0°와 90°로 교차하여 대칭적으로 적층하였다. 복합재 시편의 층간 분리 결함은 두께 방향의 가운데에 있도록 하였고, 0.03 mm 두께의 테프론 필름을 가운데 층에 부착하여, 고온 프레스 공정 후 시편 내부에 층간 분리가 유지될 수 있도록 하였다. 시편의 길이는 350 mm이고 폭은 50 mm, 두께는 1 mm이다. 시편 내부의 결함 위치를 다르게 하여, 고정단 가까운 쪽에 결함이 위치한 시편을 D1, 고정단 먼 쪽에 결함이 위치한 시편을 D2로 하였다. 층간 분리 결함의 크기는 길이 100 mm, 폭 50 mm로 하였다. 제작된 시편들의 사진을 Fig. 1(a)에 나타내었고, 세 가지 시편들의 개념도를 Fig. 1(b)에 나타내었다. 제작된 시편들의 진동 신호 측정 위치를 결정하기 위하여 유한요소해석을 수행하여 시편의 모드 형상을 확인하였고, 결과를 Fig. 2에 나타내었다. 폭이 넓은 시편 형태라 굽힘 모드와 비틀림 모드가 교차하여 나타나는 것을 확인할 수 있다. 시편의 진동 신호를 길이 방향의 끝 단과 폭 방향의 가운데에서만 측정하면 굽힘 모드에 대한 정보는 포함되나, 비틀림 모드에 대한 정보가 포함되지 않게 되므로, 진동 측정은 폭 방향의 끝 쪽에 센서를 부착하여 수행하도록 하였다. 제작된 복합재 시편의 진동 신호를 측정하기 위한 측정 위치를 Fig. 3에 나타내었다. Fig. 3에서 원형점으로 표시된 위치가 학습 데이터로 사용하기 위한 진동 신호를 측정한 위치이다. 길이 방향으로 동일한 30 mm의 간격으로 열 개의 위치에 가속도계를 부착하여 반복해서 진동 신호를 측정하고, 각 위치에서 20회 반복 측정을 수행하여 전체 200개의 학습 데이터를 확보하였다. Fig. 3에서 삼각형으로 표시된 위치는 테스트 데이터로 사용하기 위한 진동 신호를 측정한 위치이다. 실제 시스템의 적용에서는 항상 동일한 위치에서 측정된 진동 신호를 이용하는 것이 어려우므로, 테스트 데이터의 측정 위치를 학습 데이터 측정 위치와 다르게 선정하여 측정 위치가 다른 경우에도 효과적으로 결함 탐지가 가능한 지 검증하였다. 각 위치에서 15회 반복 측정을 수행하여 전체 60개의 테스트 데이터를 확보하였다. Fig. 4에 진동 실험을 위한 장치와 실험 방법을 나타내었다. SIMULINK를 이용하여 0에서 1000 Hz 사이의 랜덤 신호를 생성하여 가진기를 작동하도록 하였다. 진동 신호의 측정을 위해서는 가속도계를 사용하였고, 측정된 진동 신호는 증폭 장치와 데이터 획득 장치를 통하여 컴퓨터에 데이터를 저장된다. 가진기는 방진 테이블에 고정되어 있으며, 복합재 시편의 한 쪽 끝은 제작된 지그를 이용하여 가진기에 고정되어 있다.

Fig. 1

Prepared composite specimens

Fig. 2

First six mode shapes

Fig. 3

Vibration measurement points

Fig. 4

Experimental setup

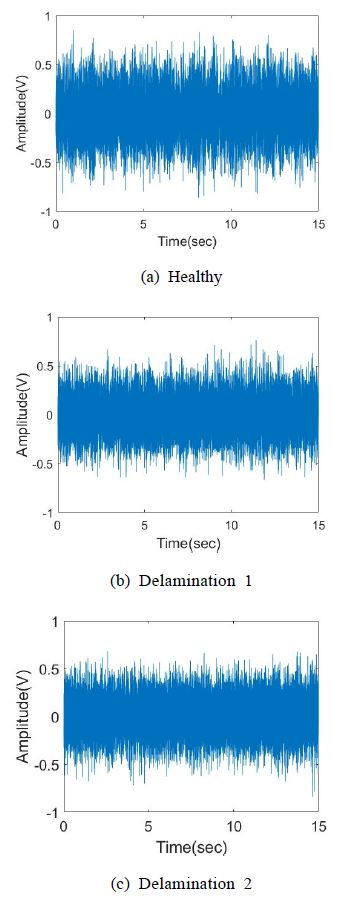
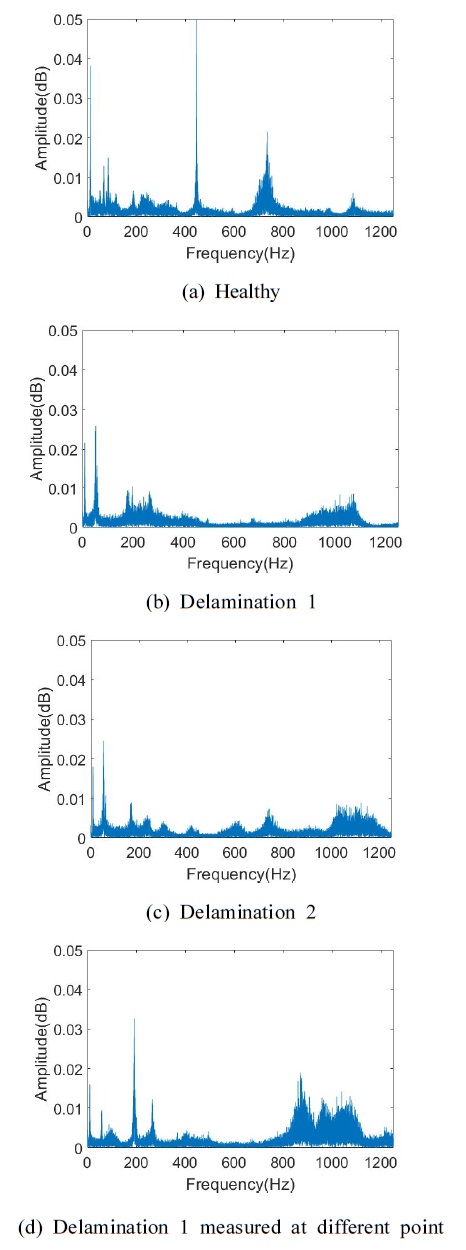
측정된 세 가지 다른 시편의 끝 단에서 측정한 진동 신호의 시간 응답과 주파수 응답을 Fig. 5와 Fig. 6에 각각 나타내었다. Fig. 5에 나타낸 시간 응답에서는 결함이 없는 시편과 결함이 있는 시편의 차이를 확인하기 어려운 것을 확인할 수 있다. Fig. 6에 나타낸 결함이 없는 시편과 결함이 있는 시편의 주파수 응답에서는 주파수 성분과 크기가 다소 차이가 있는 것을 확인할 수 있다. 일반적으로 층간 분리 결함이 있으면 공진 주파수가 감소하는 특성을 나타내나 이 연구에서 사용한 1000 Hz 이하의 저주파수 영역에서는 그 차이가 크게 나타나지 않는다. 또한, Fig. 6(b)와 Fig. 6(d)에 나타난 것과 같이 동일한 시편에서도 측정 위치에 따라 주파수 응답 특성이 다르게 나타날 수 있으므로, 주파수 성분과 크기 차이만으로 결함의 유무 또는 결함의 위치에 대한 분류를 수행하기에는 한계가 있다. 또한, 시간 응답과 주파수 응답에서는 각각 주파수 특성과 시간에 대한 특성 정보가 나타나지 않는 한계가 있으므로, 이 연구에서는 시간 특성과 주파수 특성을 동시에 표현할 수 있는 스펙트로그램(spectrogram) 데이터를 이용하여 결함을 탐지하고 결함 위치 분류를 수행한다.

Fig. 5

Time responses of the specimens

Fig. 6

Frequency responses of the specimens

3. 탐지 및 분류

3.1 오토인코더

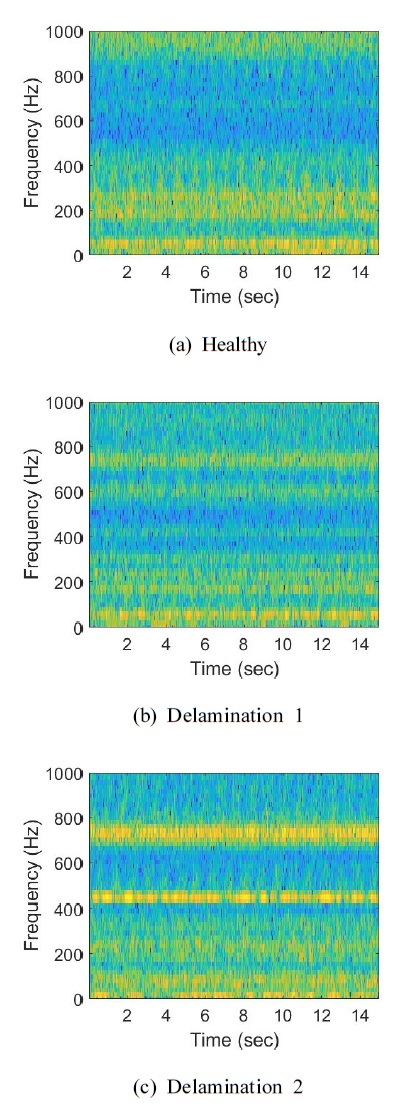
먼저, 결함의 유무만을 탐지할 수 있는 단순한 기법으로 오토인코더를 적용하였다. 오토인코더에 입력 데이터로 사용하기 위하여 측정된 진동 데이터를 단시간 퓨리에 변환을 통하여 이차원 이미지 데이터 변환하고 이를 Fig. 7에 나타내었다. 오토인코더는 입력 데이터의 정보를 압축하는 인코더와 압축된 정보로부터 입력 데이터를 다시 재생해 내는 디코더로 구성되어 있으며, 일반적으로 이미지 등의 입력 데이터와 유사한 특성을 갖는 데이터를 생성하기 위해 사용된다. 결함이 없는 복합재 시편의 데이터를 생성할 수 있도록 학습된 오토인코더 모델에 결함이 없는 복합재 시편의 테스트 데이터를 입력하면 출력된 데이터와 입력 데이터 사이의 오차가 작게 발생하지만, 결함이 있는 시편의 테스트 데이터를 입력하면 이에 대해서는 학습이 잘 되어있지 않으므로 출력 데이터와 입력 데이터 사이의 오차가 크게 발생하게 된다. 이러한 오차의 크기를 비교하여 결함의 유무를 판별할 수 있다. 입력 데이터와 출력 데이터 사이의 오차는 다음 식과 같은 평균제곱오차를 이용한다.

$\[ \frac{1}{m}\sum _{i=1}^m{\left(x_i-\widehat{x_i}\right)}^2 \]$

(1)

Fig. 7

Images from short-time fourier transformation

여기서 x_i는 입력 데이터, $$ \widehat{x_i}$$은 출력 데이터, m은 전체 데이터의 갯수이다.

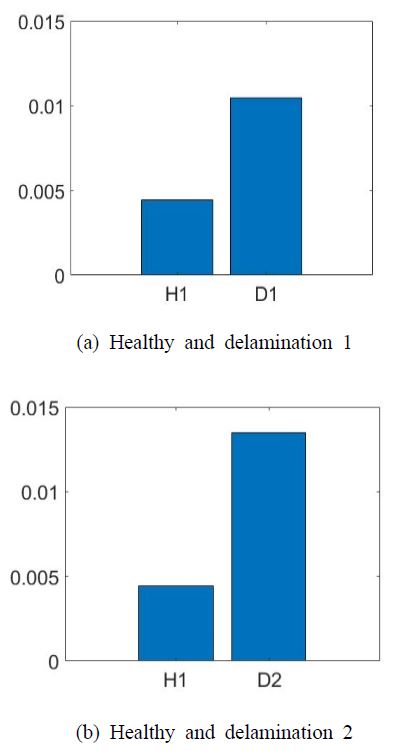
결함이 없는 복합재 시편의 학습 데이터 200개를 입력으로 하여 오토인코더 모델을 학습한다. 학습된 모델에 결함이 없는 시편의 테스트 데이터 60개와 D1 결함이 있는 복합재 시편의 테스트 데이터 60개를 입력하여 출력과 입력 사이의 오차를 계산하고 결과를 Fig. 8(a)에 나타내었다. D1 결함이 있는 경우 오차값이 더 크게 나타나는 것을 확인할 수 있다. 동일한 오토인코더 모델에 결함이 없는 시편의 테스트 데이터 60개와 D2 결함이 있는 복합재 시편의 테스트 데이터 60개를 입력하여 출력과 입력 사이의 오차를 계산하고 결과를 Fig. 8(b)에 나타내었다. D1 또는 D2 결함이 있는 경우, 결함이 없는 경우보다 출력과 입력 사이에 더 큰 오차값을 갖는 것을 확인할 수 있다. 오토인코더를 통해 생성된 출력과 입력을 비교하여 오차를 계산하고, 특정 값을 기준으로 오차가 더 작을 경우 결함이 없고, 더 클 경우 결함이 있다고 판단할 수 있다. Fig. 8의 결과에서는 0.005에서 0.006 사이의 값을 결함 유무를 판단하는 기준값으로 사용할 수 있을 것이다.

Fig. 8

Mean square errors between healthy and damaged composite specimen

3.2 심층 신경망

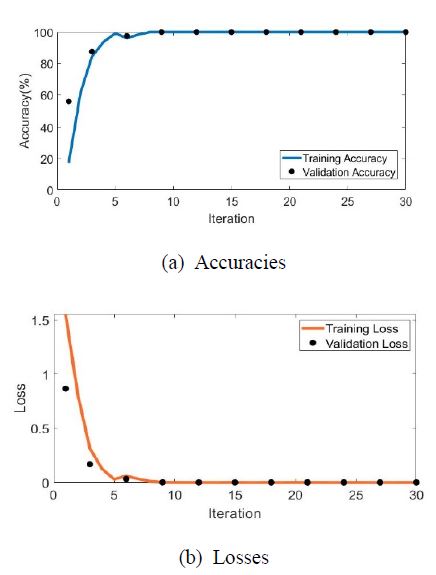
오토인코더를 이용할 경우 결함의 유무는 판단할 수 있었지만, 결함의 위치가 다른 시편을 구분할 수는 없다. 따라서, 결함의 위치가 다른 두 종류의 시편을 분류할 수 있도록 심층 신경망 알고리즘을 이용하였으며, 심층 신경망 중에서도 합성곱 신경망(convolutional neural network, CNN)을 이용하였다. 이 연구에서는 CNN 알고리즘의 사용을 위해 MATLAB 소프트웨어를 이용하였다. 또한 CNN 알고리즘의 학습과 테스트를 위해 활용된 이미지는 135 × 171 × 3의 크기를 가진다. 구성한 CNN 알고리즘은 총 15개의 layer를 가지며, 이를 Table 1에 나타내었다. 학습률(learning rate)은 loss가 충분히 빨리 감소하는 0.001로 설정하였으며, 반복(iteration) 3, 정확도의 수렴을 확인하기 위해서 반복 학습(epoch) 10으로 훈련을 진행하였다. 또한, 3회 반복(iteration)마다 검증(validation)을 진행하였고, 이에 따른 훈련 정확도와 검증 정확도는 Fig. 9(a)에 훈련 손실 및 검증 손실은 Fig. 9(b)에 각각 나타내었다.

Table 1

Structure of the CNN model

Fig. 9

Training curves of the CNN model

훈련된 CNN을 이용해 테스트를 진행한 결과를 Fig. 10에 나타내었다. 각 클래스 별로 입력 데이터와 다른 곳에서 측정된 60개의 테스트 데이터를 이용해 테스트를 진행한 결과, 결함이 있는 D2의 데이터를 결함이 없는 경우로 잘못 분류하는 경우가 발생하였으나, 결함이 없는 경우와 D1 결함이 있는 경우는 매우 정확하게 분류하는 것을 확인할 수 있다. 학습 데이터와 훈련 데이터의 측정 위치를 다르게 한 경우에도 97.2 %의 높은 분류 정확도를 갖는 것을 확인할 수 있으며, 상당히 높은 정확도로 결함의 위치가 다른 구조물 시편들을 분류할 수 있는 것을 확인하였다.

Fig. 10

Confusion matrix

4. 결 론

이 연구에서는 구조물에서 측정된 진동 신호와 심층 신경망을 이용하여 적층 복합재 구조물에 발생한 층간 분리 결함을 탐지하는 기법을 검증하였다. 특히 결함 탐지 및 분류를 위한 학습 데이터와 테스트 데이터의 진동 측정 위치를 달리하여 측정 위치 변화에 강건함을 가질 수 있는지 확인하였다. 결함이 없는 복합재와 서로 다른 위치에 결함이 있는 두 개의 복합재 구조물에 랜덤 가진에 대한 진동 신호를 측정하고, 단시간 푸리에 변환을 통해 이미지로 변환한다. 오토인코더의 입력과 출력 사이의 오차를 확인하여 구조물의 결함 유무를 탐지하는 것이 가능함을 확인하였다. 또한 심층 신경망을 적용하여 결함이 없는 구조물과 결함의 위치가 서로 다른 두 구조물에 대한 분류가 가능함을 확인하였다. 이 연구에서는 결함이 있는 구조물에 대한 실험 데이터도 충분히 확보한 상태에서 연구를 수행하였으나, 실제 환경에서는 결함이 있는 구조물의 데이터를 다량 확보하는 것은 어려운 단점이 있다. 이에 다음 단계 연구에서는 데이터 증강 기법을 적용하여 결함 탐지 성능을 검증할 계획이다.

Acknowledgments

이 연구는 과학기술정보통신부 및 정보통신기획평가원의 Grand ICT연구센터지원사업의 연구결과로 수행되었음(IITP-2021-2020-0-01612). 또한 이 논문은 2020년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업임(No. 2020R1I1A3074547).

References

• Saravanos, D. A. and Hopkins, D. A., 1996, Effects of Delaminations on the Damped Dynamic Characteristics of Composite Laminates: Analysis and Experiments, Journal of Sound and Vibration, Vol. 192, No. 5, pp. 977~993. [https://doi.org/10.1006/jsvi.1996.0229]
• Cho, M. and Kim, J. S., 2001, Higher-order Zig-zag Theory for Laminated Composites with Multiple Delaminations, Journal of Applied Mechanics, Vol. 68, No. 6, pp. 869~877. [https://doi.org/10.1115/1.1406959]
• Radu, A. G. and Chattopadhyay, A., 2002, Dynamic Stability Analysis of Composite Plates Including Delaminations Using a Higher Order Theory and Transformation Matrix Approach, International Journal of Solids and Structures, Vol. 39, No. 7, pp. 1949~1965. [https://doi.org/10.1016/S0020-7683(01)00168-8]
• Kim, H. S., Kim, J. and Choi, S. B., 2005, Study on Dynamic Characteristics of Delaminated Smart Composite Laminates, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 15, No. 4, pp. 395~403. [https://doi.org/10.5050/KSNVN.2005.15.4.395]
• Chattopadhyay, A., Peralta, P., Papandreou-Suppappola, A. and Kovvali, N., 2009, A Multidisciplinary Approach to Structural Health Monitoring and Damage Prognosis of Aerospace Hotspots, Aeronautical Journal, Vol. 113, No. 1150, pp.799~810. [https://doi.org/10.1017/S0001924000003456]
• Swann, C. and Chattopadhyay, A., 2006, Optimization of Piezoelectric Sensor Location for Delamination Detection in Composite Laminates, Engineering Optimization, Vol. 38, No. 5, pp. 511~528. [https://doi.org/10.1080/03052150600557841]
• Sung, D. W., Oh, J. H., Kim, C. G. and Hong, C. S., 2000, Impact Damage Detection of Smart Composite Laminates Using Wavelet Transform, Journal of the Korean Society for Composite Materials, Vol. 13, No. 1, pp. 40~49.
• Kang, S. H., Jeon, J. Y., Kim, D. H., Park, G., Kang, T. and Han, S. W., 2017, Damage Detection on Thin-walled Structures Utilizing Laser Scanning and Standing Waves, Transactions of the Korean Society of Mechanical Engineers, A, Vol. 41, No. 5, pp. 401~407.
• Kim, C., Jeon, Y., Park, J. and Cho, J. Y., 2021, Image Based Damage Detection Method for Composite Panel with Guided Elastic Wave Technique: Part I. Damage Localization Algorithm, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 49, No. 1, pp. 1~12. [https://doi.org/10.5139/JKSAS.2021.49.1.1]
• Kim, C., Jeon, Y., Park, J. and Cho, J. Y., 2021, Image Based Damage Detection Method for Composite Panel with Guided Elastic Wave Technique: Part II. Size Estimation Algorithm, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 49, No. 1, pp. 13~20. [https://doi.org/10.5139/JKSAS.2021.49.1.13]
• Wang, B., Zhong, S., Lee, T.-L., Fancey, K. S. and Mi, J., 2020, Non-destructive Testing and Evaluation of Composite Materials/Structures: A State-of-the-art Review. Advances in Mechanical Engineering, Vol. 12, No. 4, pp. 1~28. [https://doi.org/10.1177/1687814020913761]
• Khan, A., Ko, D.-K., Lim, S. C. and Kim, H. S., 2019, Structural Vibration-based Classification and Prediction of Delamination in Smart Composite Laminates Using Deep Learning Neural Network, Composites Part B: Engineering, Vol. 161, 586~594. [https://doi.org/10.1016/j.compositesb.2018.12.118]