건식저장용기의 연속 충돌 경사낙하 유한요소해석

1. 서 론

국내 원자력발전소에서는 현재 사용후핵연료를 원자력발전소에 임시보관하고 있다. 하지만 계속된 원자력 발전으로 폐기물이 증가함에 따라, 현재 임시보관 중인 사용후핵연료를 중간저장시설으로 이동해서 보관해야 한다. 이를 위해 건식저장용기(dry storage cask)가 사용된다.

건식저장용기는 운송 중 낙하 사고로 인해 내부 핵연료의 방사능이 유출될 경우 매우 심각한 사고로 이어질 수 있다. 이에 따라 국제원자력기구(IAEA)에서 규정한 낙하 사고에 대한 테스트를 통해 안정성 검증을 수행한다⁽¹⁾. 국제원자력기구의 다양한 낙하 사고 조건 중, 저장용기에 가장 큰 손상을 발생시키는 9 m 자유낙하와 1 m 관통낙하 해석에 대한 연구가 많이 수행되고 있다^(2~7).

특히 낙하 높이가 높은 9 m 자유낙하 조건에 대해 많은 연구가 수행되고 있다. 9 m 자유낙하는 수직방향 낙하, 수평방향 낙하, 초기 경사각을 주고 낙하시키는 경사낙하(oblique drop) 조건이 존재한다. 경사낙하의 경우 전체 저장용기에 고르게 충격 하중이 분포하지 않고, 모서리와 같은 특정 부분에 충격 하중이 집중되어 수직 및 수평낙하 보다 저장용기에 큰 손상을 유발할 수도 있고, 수직 및 수평낙하 보다 충돌 거동을 분석하기가 까다롭기 때문에, 이에 대한 연구가 필요하다.

건식저장용기의 경사낙하는 bottom 영역이 먼저 지면에 충돌하는 경우와 top 영역이 먼저 지면에 충돌하는 경우로 나뉘고, 수직방향 낙하에서 경사 조건을 준 corner drop과 수평방향 낙하에서 경사 조건을 준 slap down drop으로 나뉜다. 이 연구에서는 9 m bottom slap down 경사낙하 조건에 대해 해석을 수행했다.

Slap down 경사낙하 조건에서는 먼저 지면에 충돌하는 1차 충돌보다, 1차 충돌에 이어 발생하는 2차 충돌이 저장용기에 더 큰 충돌 응답을 유발하는 것으로 알려져 있다. 2차 충돌 응답을 기준으로 저장용기의 최대 충돌 응답이 발생하는 각도를 찾는 것이 중요한 이슈 사항이다. 이와 관련해서 많은 연구 등에서 건식저장용기의 최대 충돌 응답 발생 각도에 대한 연구가 수행되었다^(2,5,6).

이 연구에서는 bottom slap down 낙하 해석을 유한요소해석을 통해 수행하고, 최대 충돌 응답 발생 각도를 도출한다. 유한요소해석 프로그램은 충돌 해석에 널리 활용되고 있는 ANSYS LS-DYNA를 통해 수행한다. Bottom slap down 낙하에 대해 최대 충돌 응답 발생 각도를 2차 충돌 속도와 바닥면 반력을 통해 도출한다. 또한 건식저장용기 내부 구조 caniser와 disc에서 최대응력이 발생하는 구조적 취약부를 확인한다.

2. 건식저장용기 경사 낙하 해석

2.1 유한요소 해석 모델

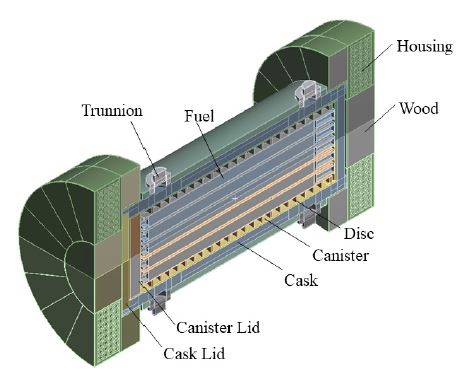
건식저장용기는 크게 impact limiter, cask, canister, disc, 핵연료로 구성되어 있으며, 전체 중량은 약 125톤이다. 해석 모델은 대칭성을 고려해서 Fig. 1과 같이 1/2 모델로 구성했으며, 총 785 316개의 요소로 모델링 되었다. 해석은 ANSYS LS-DYNA를 통해 수행했다.

Fig. 1

Structure of dry storage cask

건식저장용기의 각 구조의 모델링 방법에 대해 설명하면, 먼저 충돌 완충을 위해 설계된 impact limiter는 housing과 wood로 구성되어 있으며, 충돌에너지의 대부분을 흡수한다. Wood는 crushable foam 재료모델을 사용했고, housing은 isotropic bi-linear hardening 모델을 사용했다.

Impact limiter 안쪽에 저장용기을 보호하는 두꺼운 두께의 cask 구조가 있다. Cask와 impact limiter는 볼트로 연결되어 있는데, 이 연구에서는 볼트를 상세모델링 하지는 않고 node merge를 통해 볼트부의 cask와 impact limiter의 노드를 연결시켰다. Cask body와 lid도 원래 볼트를 통해 연결되지만, bonded contact 조건을 통해 구현되었다. 이렇게 볼트부를 단순하게 모델링한 이유는, 이 논문의 목적이 거시적인 경사낙하 거동을 주로 확인하기 위한 목적이기 때문에, 전체 거동에 영향이 거의 없는 볼트부는 상세하게 모사하지 않은 것이다.

Cask 안쪽에는 핵연료를 담는 canister 구조가 있다. Canister는 bottom 부에서 cask와 연결된다. 연결부는 bonded contact 조건을 적용했다. Canister 내부에는 핵연료를 지지하는 총 24개의 disc 구조가 있다. Disc와 canister는 약간의 유격이 존재하는데, 경사낙하 충돌 시 2차 충돌 부근에서 canister와 disc 간의 내부 충돌이 발생한다. 내부 구조 간의 충돌은 single surface contact 조건을 통해 반영한다. Cask, canister, disc는 모두 isotropic bi-linear hardening 모델을 적용했으며, Table 1에 각 건식저장용기 구조별 적용된 재료 물성을 도시했다.

Table 1

Material properties of dry storage cask

2.2 경사낙하 해석 조건

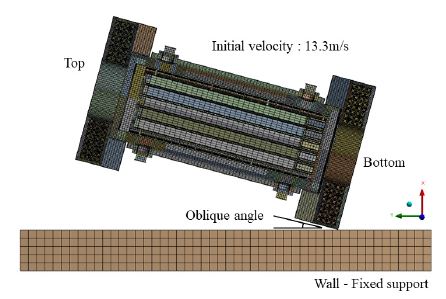
낙하 해석 조건은 국제원자력기구(IAEA)에 명시된 낙하 조건대로 건식저장용기의 가장 낮은 위치의 모서리에서 바닥면까지의 높이를 9 m로 설정했다. Fig. 2에 낙하 해석 조건을 나타내었다. 따라서 모서리와 바닥면이 처음 충돌할 때의 초기 속도는 음의 x방향으로 13.3 m/s이다. 중력 조건 역시 음의 x방향이다. 경사낙하조건은 bottom slap down 낙하로서 바닥면과 저장용기 사이의 각도를 0° ~ 30°로 변경시키며 해석을 수행했다. 이 연구에서는 거시적인 거동에 초점을 맞춰서 경향성을 분석했기 때문에 각도는 5° 단위로 변경했다.

Fig. 2

Oblique drop analysis conditions

바닥면은 전체 면에 대해 fixed support 조건을 적용했다. 따라서 바닥면은 고정된 rigid body와 같다. 이렇게 바닥면을 강체로 모델링하면, 저장용기에 더 큰 충돌 데미지가 발생하기 때문에 보다 보수적인 해석이 가능하다. 바닥면의 변형이 일어나지 않아 충돌에너지가 모두 저장용기의 변형에너지로 전환되며, 바닥면의 강성이 매우 높게 설정되서 충돌 시간도 짧아지기 때문에 저장용기에 가해지는 충돌력의 최대 크기가 더 커지기 때문이다.

2.3 경사낙하 각도별 해석 결과 및 최대 충돌응답 발생 각도 확인

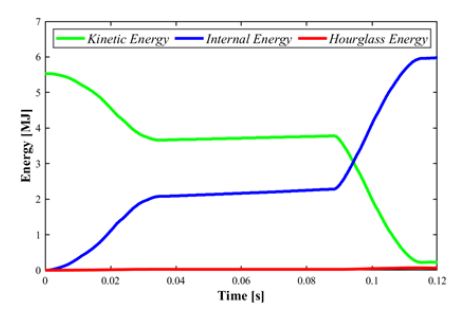
해석 수행 결과, 초기 운동에너지가 변형에너지인 내부에너지로 전환되고, hour glass 에너지는 변형에너지의 1 % 수준으로 나타났다. Fig. 3에 에너지 그래프를 도시했다.

Fig. 3

Oblique drop energy graph

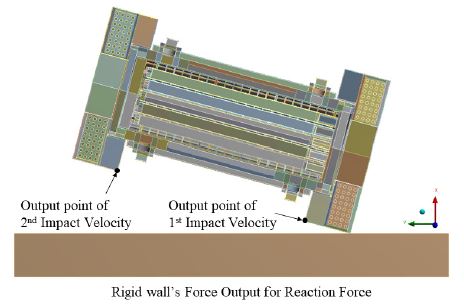
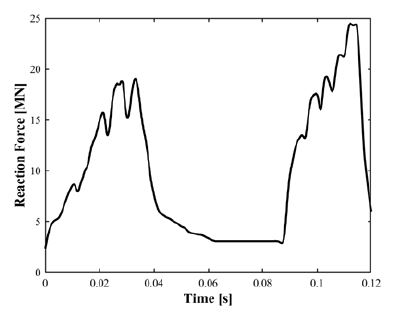
충돌 해석결과는 충돌 속도와 바닥면 반력의 충돌 응답을 통해 분석한다. 위의 물리량을 이용하는 이유는 충돌 속도와 힘이 가장 저장용기의 거시적 충돌 거동을 잘 표현할 수 있기 때문이다. Fig. 4에 충돌 속도와 바닥면 반력의 결과를 도출한 위치를 표시했다.

Fig. 4

Output point position

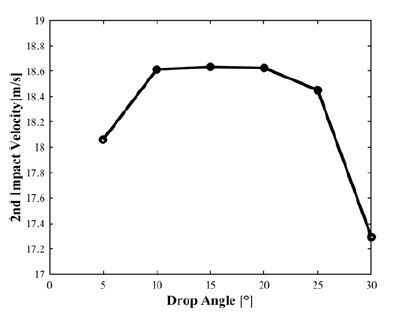
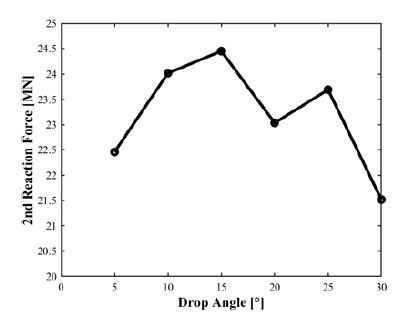
경사낙하 해석결과를 Table 2에 나타냈다. 해석을 수행한 모든 각도에 대해서 1차 충돌 응답보다 2차 충돌 응답이 크게 나타났다. 먼저, 충돌 속도의 경우 1차 충돌 속도는 13.3 m/s이지만, 2차 충돌의 경우 0° ~ 30° 모두 17 m/s 이상의 충돌 속도가 발생했다. 바닥면의 반력 또한 1차 충돌보다 2차 충돌일 때 높게 발생한다. 1차 충돌 시 최대 바닥면 반력은 19 MN 전후로 나타난다. 5도 경사각의 경우 1차 충돌보다 2차 충돌일 때 최대 바닥면 반력크기가 약 20 % 높게 나타나며, 15°는 약 30 %, 30°는 약 10 % 높게 나타난다. 30° 경사각까지 데이터를 나타낸 이유는 30°까지의 데이터로 경향성이 충분히 확인되기 때문이다.

Table 2

Impact velocity and Maximum Reaction Force by drop angle

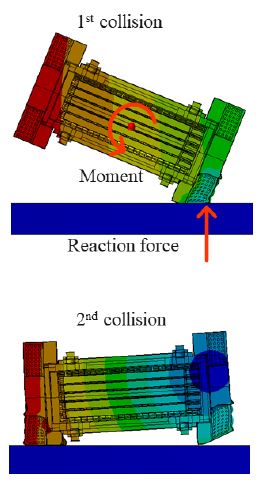
2차 충돌 응답이 1차 충돌보다 크게 발생하는 이유는, 1차 충돌 작용점과 저장용기의 질량중심이 같은 작용 선상에 위치하지 않기 때문에, 저장용기에 모멘트가 발생해서 회전운동을 하기 때문이다. Fig. 5에 저장용기의 1차 충돌과 2차 충돌 현상을 도시했다.

Fig. 5

Macroscopic analysis of bottom slap down drop

Table 2에 각도 별 2차 충돌 속도와 2차 충돌시 최대 바닥면 반력 값을 통해 15° 각도에서 가장 큰 충돌 응답이 발생하는 것을 알 수 있다. 경향성은 15° 각도 전후로 응답이 감소하는 것으로, 이전에 수행한 slap down drop 연구들의 경향성과 일치한다. Fig. 6과 Fig. 7의 그래프에 각도별 2차 충돌 속도와 최대 바닥면 반력 값의 경향성을 나타냈다.

Fig. 6

Maximum 2nd impact velocity by drop angle

Fig. 7

Maximum 2nd reaction force by drop angle

최대 충돌 응답이 15°에서 발생한 이유는, 먼저 15° 이상 각도에 대해서는 저장용기의 무게중심점과 1차 충돌점과의 거리가 가까울수록, 1차 충돌부에서 충돌에너지를 더 많이 흡수하기 때문이다. 하지만, 15° 각도 이하의 경사각으로 낙하할 경우, 체공 시간이 짧아 1차 충돌 후 모멘트로 인한 2차 충돌 속도 증가가 충분히 일어나기 전에 충돌하기 때문에 15° 보다 낮은 충돌 응답이 나타나는 것으로 보인다.

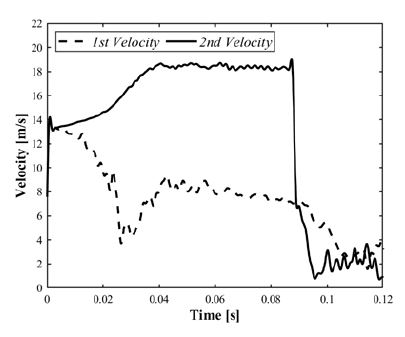
Fig. 8과 Fig. 9에 15° 경사낙하에서의 시간에 따른 속도 그래프와 바닥면 반력 그래프를 나타냈다. 약 0.06 s까지 1차 충돌이 발생하며, 약 0.02 s의 체공 시간 후 2차 충돌이 발생한다.

Fig. 8

1st and 2nd impact velocity at 15° drop

Fig. 9

Reaction force at 15° drop

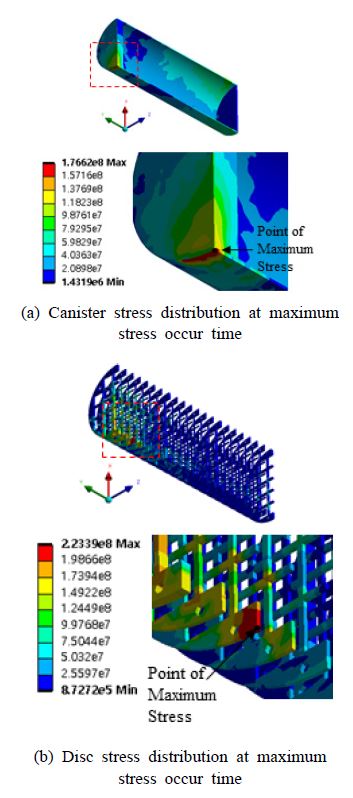
거시적인 충돌 거동을 나타내는 충돌 속도와 바닥면 반력 외에, 경사 각도에 따라 건식저장용기 내부 구조의 충격 응답을 확인하기 위해 최대 응력 결과를 확인했다. 내부 구조인 canister와 disc의 최대 응력은 2차 충돌 발생 부근에서 구조 간 추가 충돌이 발생하는 영역에서 발생했다. Fig. 10에 각 내부 구조의 최대 응력 발생 위치와 최대 응력이 발생할 때 응력 분표를 도시했다.

Fig. 10

Stress distribution of internal structures

내부 구조의 최대 응력은 거시적인 충돌 거동 외에 내부 복잡한 충돌 현상에 따라 경향성이 달라지지만, 5°, 15°, 30° 경사낙하의 해석 결과를 비교해보면, 거시적 충돌 응답 경향성과 동일하게 15°에서 최대 응력 값이 발생하는 것을 Table 3에서 확인할 수 있다.

Table 3

Maximum stress value of internal structures

3. 결 론

이 연구에서는 유한요소해석을 통해 건식저장용기 경사낙하 해석을 수행했다. 경사낙하 해석은 9 m Bottom slap down 낙하 조건으로 0° ~ 30° 각도 범위에서 수행했다. 충돌 속도와 바닥면 반력으로 충돌 응답을 확인했으며, 모든 각도 조건에서 1차 충돌 응답보다 2차 충돌 응답이 크게 나타났다. 최대 충돌 응답이 발생하는 각도는 15°로 나타났다. 15° 경사낙하 시 건식저장용기 내부 구조인 cask, canister, disc 간에 추가 충돌이 발생하며, 추가 충돌이 발생하는 부분에서 최대 응력이 발생했다. 최대 응력 결과도 15° 각도에서 가장 높게 나타났다.

Acknowledgments

이 성과는 정부(과학기술통신부)의 재원으로 한국연구장학재단의 지원을 받아 수행된 연구임(No.2019M2D2A2048296).

References

• International Atomic Energy Agency(IAEA), 2005, Regulations for the Safe Transport of Radioactive Material 2005 Edition, Section 7, TEST PROCEDURES, pp. 99~109.
• Ku, J. H., Seo, K. S., Kang, H. Y. and Kim, Y. J., 1995, A FEM Analysis of the Dynamic Behaivor of Spent Nuclear Fuel Transport Cask under Oblique Drop Impact, Transactions of the KSME, A, Vol. 19, No. 12, pp. 3252~3259.
• Jaksic, N. and Nilsson, K.-F., 2009, Finite Element Modelling of the One Meter Drop Test on a Steel Bar for the CASTOR Cask, Nuclear Engineering and Design, Vol. 239, No. 2, pp. 201~213. [https://doi.org/10.1016/j.nucengdes.2008.10.010]
• Kim, K.-S., Kim, J.-S., Choi, K.-S., Shin, T.-M. and Yun, H.-D., 2010, Dynamic Impact Characteristics of KN-18 SNF Transport Cask – Part 1: An advanced Numerical Simulation and Validation Technique, Annals of Nuclear Energy, Vol. 37, No. 4, pp. 546~559. [https://doi.org/10.1016/j.anucene.2009.12.023]
• Saito, Y., Kishimoto, J., Matsuoka, T., Tamaki, H. and Kitada, A., 2014, Containment Integrity Evaluation of MSF-type Cask for Interim Storage and Transport of PWR Spent Fuel, International Journal of Pressure Vessels and Piping, Vol. 117-118, pp. 33~41. [https://doi.org/10.1016/j.ijpvp.2013.10.007]
• Ammerman, D. J., 2013, Spent Fuel Transportation Risk Assessment: Cask Impact Analyses, Packaging, Transport, Storage & Security of Radioactive Material, Vol. 24, No. 3, pp. 121~127. [https://doi.org/10.1179/1746510914Y.0000000045]
• Shin, T.-M. and Kim, K.-S., 2009, Study on the Impact-proof Internal Structure Design of a Spent Nuclear Fuel Transport Cask, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 4, pp. 370~377. [https://doi.org/10.5050/KSNVN.2009.19.4.370]