블레이드 동특성 근사모델의 확률 분석을 통한 블레이드 구조 설계
© The Korean Society for Noise and Vibration Engineering
Abstract
For a rotor system in which the hub/control design and blade OML were determined, the internal structural shape of the blade was designed using the dynamic characteristic surrogate model to maximize the difference between the rotating natural frequency and the integral multiple of the rotational operating frequency. Based on the general blade structure design procedure, an analysis procedure for generating a dynamic characteristic surrogate model was established, and design variables were selected to define the shapes of the internal components. To generate a dynamic characteristic surrogate model, a space filling design method, a type of design of experiment, was applied to generate design variable input values for database configuration. In this process, a range of design variables and constraint conditions suitable for blade design conditions were considered. Based on the analysis results of the finite element 2D sectional properties for various shape input conditions, a 1D beam model dynamic analysis was performed to build a rotation natural frequency database. Using this database, a dynamic characteristic surrogate model for the blade structure design was generated. A regression model and an artificial neural network model were used as surrogate models, and the 1st ~ 4th modes of the blade rotation natural frequency were predicted with the surrogate model and compared with the actual analysis results. Additionally, the values of design variables that can satisfy the dynamic characteristic requirement were selected through probability analysis of the two dynamic characteristic surrogate models, and the accuracy of the predicted values was also confirmed by comparing the analysis results.
Keywords:
Blade Structure Design, Natural Frequency, Design of Experiments, Regression Model, Artificial Neural Network Model, Probability Analysis키워드:
블레이드 구조 설계, 고유 진동수, 실험계획법, 회귀 모델, 인공 신경망 모델, 확률 분석1. 서 론
고속으로 회전하는 블레이드를 구조 설계할 경우 회전 운영 조건에서의 고유 진동수는 매우 중요한 검토사항이다. 회전 조건에서 블레이드의 고유 진동수가 회전 주파수의 정수배에 근접할수록 공진에 의한 진동하중이 커지기 때문이다. 높은 차수의 고유 진동수는 진동 크기가 작기 때문에 무시할 수 있으나 낮은 차수의 고유 진동수는 진동 크기가 크기 때문에 신중하게 검토해야 한다.
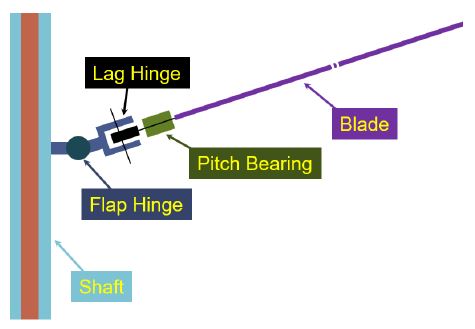
로터 시스템의 동특성에 영향을 주는 요소는 크게 허브/조종 구성품과 블레이드로 구분할 수 있다. 이 중 허브/조종 구성품은 길이가 짧고 3축 회전 힌지 역할을 하기 위해 가장 낮은 굽힘/뒤틀림 강성 단면을 포함하기 때문에 플랩/래그/뒤틀림의 1차 모드에 큰 영향을 미치게 된다(Fig. 1). 그 외 각 모드의 2차 이상의 모드에는 블레이드가 큰 영향을 미치게 된다. 이 연구에서는 허브/조종 구성품과 블레이드의 OML(outer mold line)이 결정된 블레이드에서 블레이드 내부 형상을 조절하는 설계 변수의 조절을 통해 블레이드 동특성을 예측하는 두 가지 근사모델을 생성하였으며, 두 근사모델의 확률 분석을 통해 최소 95.5 %의 확률로 동특성 요구도를 만족하는 설계 변수 값을 제시하는 구조 설계 방법을 기술하였다.
2. 본 론
2.1 블레이드 구조설계 절차 수립
블레이드 구조설계 절차는 일반적인 블레이드 구조 설계 절차와 마찬가지로 요구도 분석, 단면설계 수행, 단면 물성치 해석, 동특성/하중해석 및구조해석을 통한 요구도 만족 여부 확인으로 구성된다(1). 이 연구에서는 기본적인 구조 설계 절차를 바탕으로 근사모델 생성을 위한 해석 절차를 구성하였다.
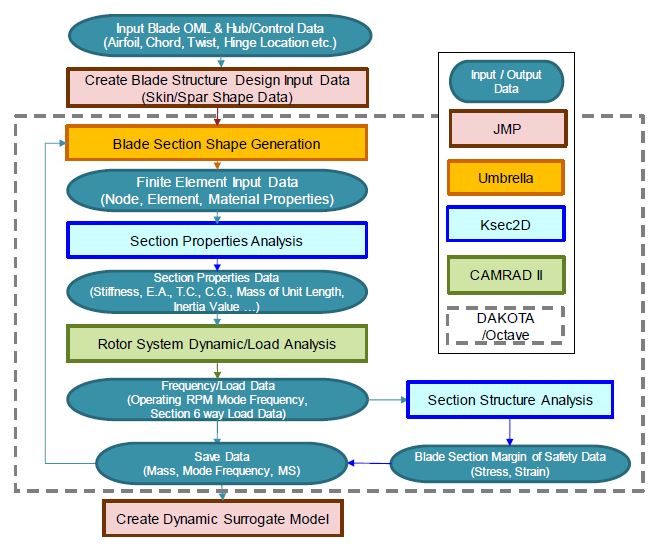
우선 해석 수행을 위한 블레이드의 OML 정보, 소재 정보 및 허브 특성 정보를 받아들인다. 그리고 실험계획법을 활용하여 블레이드 내부 구성품의 형상을 변경할 수 있도록 정의된 설계 변수 세트를 생성한다. 그리고 블레이드 OML과 각 단면별 내부 구성품 설계 변수 세트를 기반으로 블레이드 스팬 방향 단면에 대한 단면 형상을 생성한다. 이후 이를 유한요소 정보로 변환하고 단면 해석을 통해 단면 특성 정보를 획득한다. 그리고 획득된 단면 특성 정보를 기반으로 헬리콥터 통합 해석 프로그램을 통해 하중 및 동특성 정보를 획득한다. 여기서 하중 정보는 구조 해석에 적용하고, 계산된 안전여유를 앞선 과정에서 획득한 중량, 동특성과 함께 데이터 베이스로 구성한다. 그리고 모든 설계 변수 세트에 대해 해석 절차를 마치면 그 데이터 베이스를 바탕으로 근사모델을 구성하고 동특성 요구도를 만족하는 블레이드 형상을 도출한다. 이 과정에서 실험계획법을 활용한 설계 변수 세트 생성 및 데이터 베이스를 활용한 근사모델 구성은 JMP(2)를 사용하였고, 블레이드 단면 형상 생성 및 유한요소 이산화는 Umbrella(3), 단면 물성치 해석 및 단면 구조 해석은 KSec2D(4), 로터 시스템 하중/동특성 해석은 CAMRAD II(5)를 사용하였다. 그리고 이 절차들을 순차적으로 수행하고 목적값을 획득하는 드라이버로서는 Octave(6)/DAKOTA(7) 패키지를 이용하였다. Fig. 2는 동특성 요구도를 만족하는 블레이드 구조설계 근사모델을 생성하기 위한 해석 절차와 각 단계에서 사용된 소프트웨어들의 기능 및 산출물을 나타내고 있다.
2.2 블레이드 단면형상 선정 및 단면 설계 변수 분석
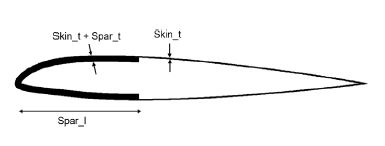
블레이드 단면 형상은 스킨-스파로 구성된 단순형상으로 선정하였다(Fig. 3). 이러한 단면 형상의 블레이드는 스킨이 뒤틀림 하중을 포함한 모든 전단하중을 감당하게 되고, 스파가 원심력을 포함한 인장하중을 감당하게 된다. 제작성이 간편한 스킨-스파 단면 형상은 스팬 길이가 상대적으로 짧고 블레이드 수가 많은 블레이드에 많이 적용된다.
블레이드 단면 설계 변수는 스킨과 스파를 구현할 수 있는 인자로 선정하였다. 먼저 스킨에 대해서는 스킨의 복합재 적층수를 나타내는 Skint를 설계 변수로 선정하였고, 스파는 스파의 복합재 적층수를 나타내는 Spart와 앞전부터 스파의 길이를 나타내는 Sparl을 설계 변수로 선정하였다.
그리고 단면 물리량 해석을 위한 블레이드 단면은 스팬 방향으로 총 10단면(rb / Rb = 0.303, 0.4, 0.5, 0.6, 0.7, 0.8, 0.85, 0.9, 0.95, 1)을 선정하였다. 그리고 그 중 블레이드 허브 체결 영역에 가까운 rb / Rb = 0.303, 0.4, 0.5 단면과 rb / Rb = 0.9, 0.95, 1단면은 각각 동일한 설계 변수를 적용하도록 하였다. 따라서 총 6개의 단면에 각각 3개의 설계 변수가 적용되어 총 18개의 설계 변수를 생성하였다. Fig. 3은 블레이드 단면 형상 및 설계 변수를 나타내고 있다.
2.3 블레이드 단면 설계 변수 생성
블레이드 단면 설계 변수 생성을 위해 실험계획법을 적용하였다. 우선 각 단면별 설계 변수들에 대해 최대값과 최소값을 설정하였다. 그리고 블레이드 구조 설계 특성을 고려하여 설계 단면이 블레이드 스팬 방향 끝단으로 갈수록 설계 변수의 값은 같거나 작아지도록 구속조건을 설정하였다.
즉, 블레이드 체결 영역의 단면 순번을 1로 설정하고, 블레이드 팁 영역으로 갈수록 순번이 증가한다고 설정하였으며 이 때, i번째 단면의 설계 변수 값은 i-1번째 단면의 설계 변수 값보다 같거나 작도록 설정하였다. Table 1은 설계 변수에 대한 범위를 나타내고 있고, 식 (1) ~ (3)은 설계 입력 변수에 대한 구속조건을 나타내고 있다.
| (1) |
| (2) |
| (3) |
where i = 1,2,3,4,5
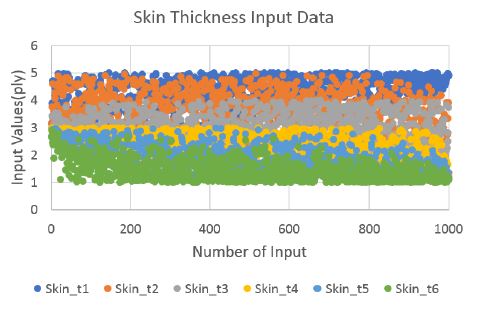
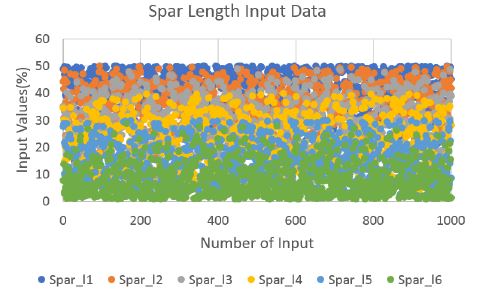
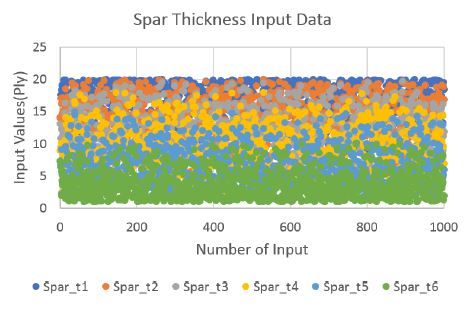
앞서 기술한 설계 변수 범위와 구속조건을 만족하는 단면 설계 변수 입력 샘플 1000 세트를 생성하였다. 설계 변수 입력 샘플 생성 방법은 공간 채움설계법(8)을 사용하였다. Figs. 4 ~ 6은 각 설계 변수에 대한 입력 샘플 생성 결과를 보여주고 있다. 이 결과는 각 설계 변수 별로 생성된 값들이 Table 1에서 정의한 설계 변수 범위 내에 들어가 있으며, 동시에 구속조건 식 (1) ~ (3)을 만족하여 i번째 단면의 설계 변수값은 i-1번째 단면의 설계 변수값보다 같거나 작음을 보여준다.
2.4 블레이드 동특성 근사모델 생성
1000세트의 설계 변수 입력 샘플에 대해 Fig. 2의 해석 절차를 수행하여 각 설계 변수에 대한 블레이드 동특성 자료를 확보한 후, 이를 기반으로 블레이드 동특성 근사모델을 생성하였다. 근사모델 생성은 데이터 베이스를 기반으로 통계적 기법을 통해 입력변수 값에 대한 결과를 예측하는 회귀(regression) 근사모델(9)과 인간의 뉴런 동작 원리를 기초로 하여 입력층에서 은닉층을 거쳐 출력층으로 전파되는 과정에서 각 뉴런들이 가지는 가중치와 바이어스 값을 조절하여 목적값을 예측하는 인공신경망(artificial neural networks, 이하 ANN) 근사모델(10)을 사용하였다.
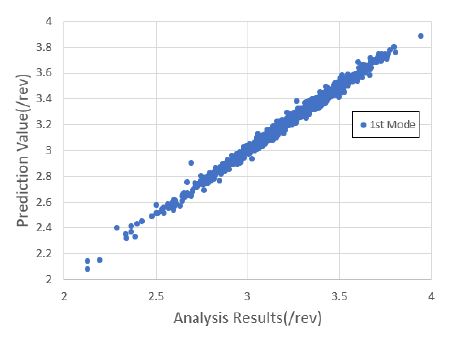
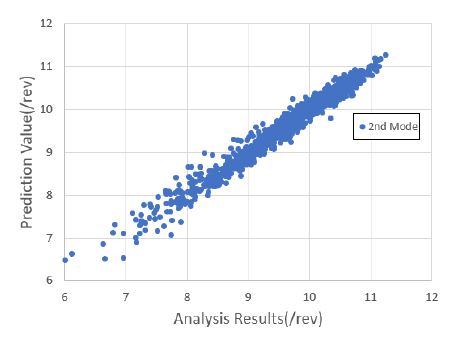
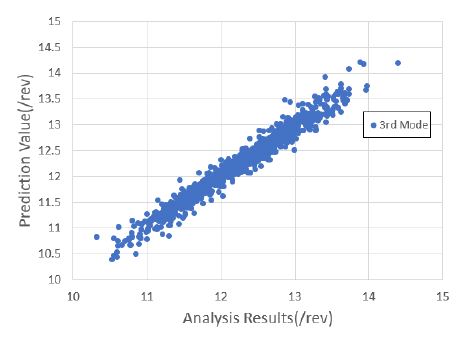
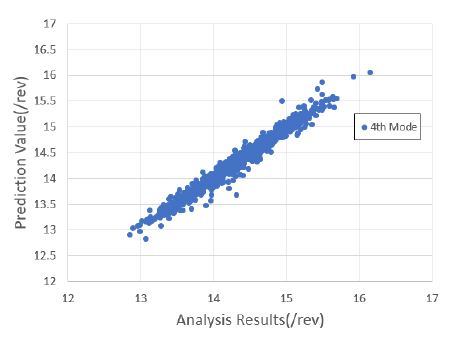
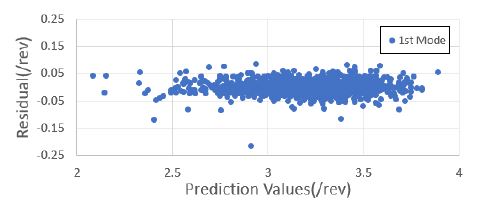
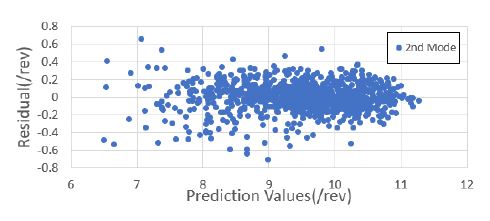
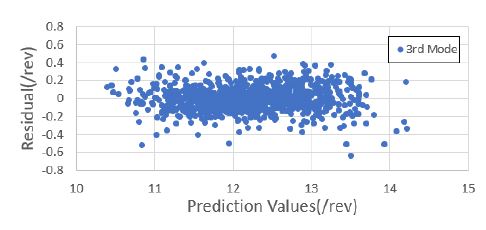
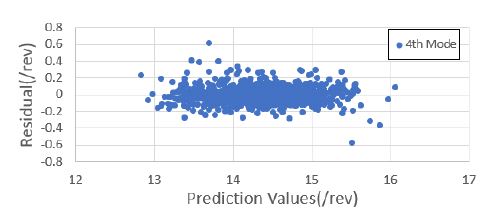
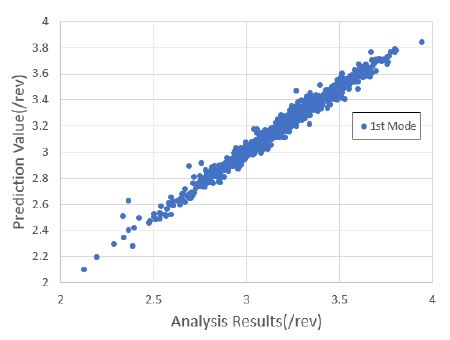
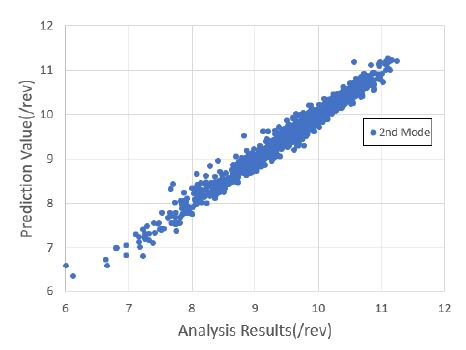
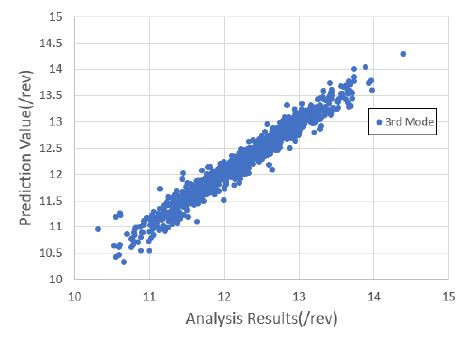
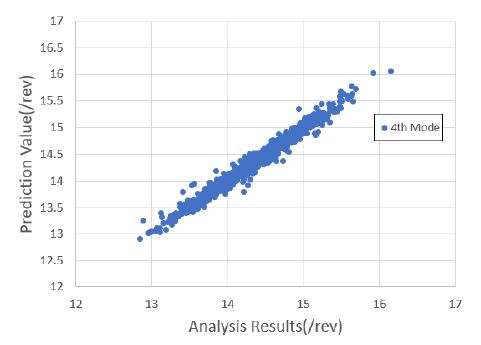
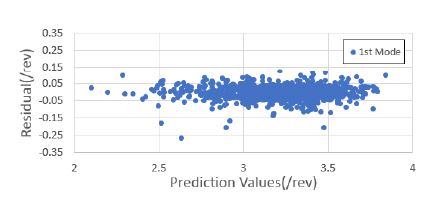
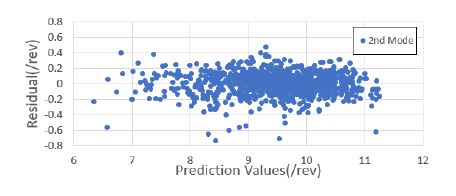
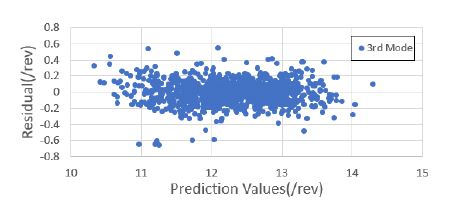
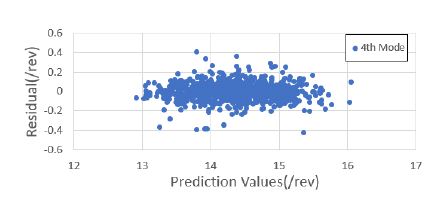
1000세트의 해석 정보를 기반으로 블레이드의 운영 회전수에 대한 고유 주파수를 예측하였다. 낮은 주파수를 기준으로 총 4개의 모드 주파수를 예측하였으며, 이를 위해 4개의 회귀 모델을 생성하였다. 모두 주파수 예측을 위한 회귀 모델은 근사모델 변수로 설계 입력 변수 외에 설계 입력 변수의 제곱과 각 설계 변수 간의 교차곱을 적용한 표준 최소 자승 모델을 사용하였다. Figs. 7 ~ 10은 1000세트의 샘플에 대한 해석값과 회귀 모델을 통한 예측값과의 비교 결과를 보여주고 있으며, Figs. 11 ~ 14는 해석값 대비 예측값의 잔차를 나타내고 있다. 그리고 Table 2는 4개의 모드 주파수에 대한 회귀 모델 예측값들의 상관 계수 제곱 R2(square of the correlation co-efficient)과 잔차에 대한 표준편차 σr를 나타내고 있다.
Figs. 7 ~ 10을 통해 알 수 있듯이, 4개의 모드에 대한 예측값은 해석값에 근사함을 알 수 있다. 그리고 Figs. 11 ~ 14를 통해 잔차가 만족스럽게 분포되어 있어, 샘플이 고르게 생성되었음을 알 수 있다(11). 또한 Table 2를 통해 R2이 모두 0.95 이상이므로 설계 변수에 대한 결과 영향도가 매우 높음을 알 수 있다.
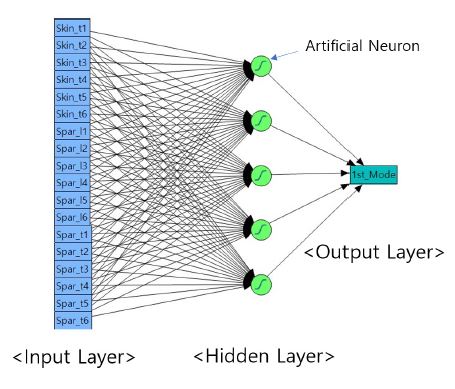
회귀 모델과 마찬가지로, 동일한 1000세트의 샘플을 기반으로 4개의 모드 주파수 예측을 위해 인공 신경망 알고리즘을 이용하여 4개의 근사모델을 생성하였다. 근사모델 생성에 사용된 뉴런의 개수는 3~10개의 조합을 반복학습 시켰으며 그 결과 뉴런의 개수가 5개 이상 넘어가게 되면 훈련에 사용된 손실 함수(loss function)인 평균 제곱 오차(mean squared error, MSE) 값이 더 이상 크게 줄어들지 않음을 확인하여 5개를 사용하였다. Fig. 15는 인공 신경망 모델의 다이어그램을 나타내고 있으며, 식 (4)는 인공 뉴런에 적용된 sigmoid 함수를 나타내고 있다.
| (4) |
where A, B, Ci = constant values
constant vector
input vector
훈련에는 666개의 샘플이 사용되었으며, 훈련된 모델의 성능 검증을 위해 나머지 샘플 334개가 사용되었다. Figs. 16 ~ 19는 1000개의 해석 정보에 대한 해석값과 인공 신경망 모델을 통한 예측값의 비교를 나타내고 있으며, Figs. 20 ~ 23은 해석값 대비 예측값의 잔차를 나타내고 있다. 그리고 Table 3은 4개의 모드 주파수에 대한 인공 신경망 모델 예측값들의 R2과 σr를 나타내고 있다.
Figs. 16 ~ 19를 통해 알 수 있듯이, 4개의 모드에 대한 예측값은 회귀 모델 결과와 마찬가지로 해석값에 근사함을 알 수 있다. 그리고 Figs. 20 ~ 23을 통해 잔차의 분포 또한 만족스럽게 분포되어 있음을 알 수 있다. 또한 Table 3의 R2값에 대한 학습결과(training)와 검증결과(validation)의 차이는 모든 모드에 대하여 최대 3 %이하 수준으로 매우 근소한 차이를 보였다. 검증결과 R2이 모두 약 0.95 이상으로서 인공 신경망 모델이 실제 해석 결과에 대한 예측 정확도가 높음을 알 수 있으며. 이때, 인공 신경망 모델의 예측 결과를 회귀 모델 결과와 비교해 보면, 1차 모드는 회귀 모델이, 2차 모드는 인공 신경망 모델이 더 정확하게 예측할 것으로 판단할 수 있다. 그리고 3, 4차 모드는 두 모델이 비슷한 상대오차를 나타낼 것으로 판단할 수 있다.
2.5 확률 분석을 통한 블레이드 구조 설계
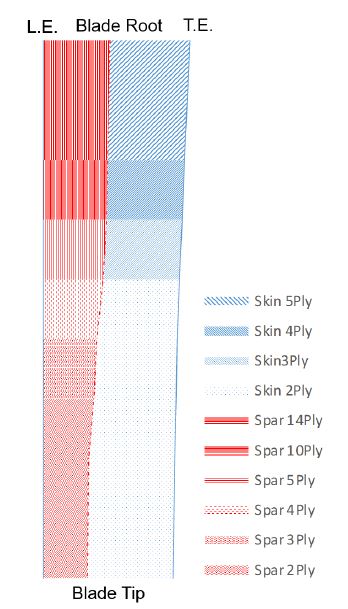
앞서 기술한 두 근사모델을 기반으로 회전 주파수의 정수배와 고유 진동수가 최대한 이격되는 구조 설계를 수행하였다. 먼저 1 ~ 4차 모드 주파수가 회전 주파수의 정수배와 0.2/rev 이상 이격되도록 동특성 요구도를 선정하였다. 그리고 두 근사모델의 각 모드별 σr을 고려하여, 근사모델을 통해 요구도를 만족하도록 구조 설계된 블레이드의 동특성 해석 결과가 요구도를 만족할 확률이 95.5 % 이상이 되도록 두 근사모델의 예측값 ±2σr 범위에서 요구도를 모두 만족하는 설계 변수를 선정하였다. 그리고 선정된 형상에 대해 해석을 수행하여 실제 해석 결과를 도출하고 근사모델을 통해 예측한 모드 주파수 값과의 차이를 확인하였다. Table 4는 선정된 설계 변수를 보여주고 있으며, Fig. 24는 그에 따른 블레이드 구조 설계 결과를 나타내고 있다. 스킨의 복합재 적층수는 블레이드 단면을 기준으로 전체 코드에 동일하게 적용되므로 스킨만 적용되는 블레이드 뒷전(trailing edge, 또는 T.E) 영역에 각 무늬별로 적층수를 정의하여 표현하였다. 반면에 스파는 블레이드 앞전(leading edge, 또는 L.E.)을 기준으로 스파 적용 길이와 복합재 적층 수를 나타내야 하므로, 점선을 통해 앞전으로부터 적용된 스파 길이를 나타내었으며 무늬를 통해 스파의 복합재 적층 수를 나타내었다.
그리고 Table 5는 선정된 설계 변수에 대한 95.5 % 확률의 모드 주파수 예측값 범위를 보여주고 있으며, Table 6은 그에 따른 블레이드 모드 주파수의 해석값과 각 근사모델의 예측값 그리고 그에 대한 상대오차를 나타내고 있다.
Table 6의 결과를 통해 4개의 모드 주파수가 2 % 이내의 오차로 예측되었으며, 해석을 통한 모드 주파수가 모두 0.2/rev 이상 이격되어 설계 목표를 만족하였음을 확인할 수 있었다. 1, 2, 4차 모드 주파수의 경우 두 근사모델의 분석 결과와 동일한 경향의 결과를 나타내었고 3차 모드의 경우는 두 근사모델의 분석 결과와 다르게 인공 신경망 근사모델이 상대적으로 더 정확한 결과를 나타내었으나, 설계 목표를 만족하는 것에는 크게 큰 문제가 없음을 확인하였다.
3. 결 론
이 논문에서는 허브/조종 형상과 블레이드 OML이 결정된 로터 시스템에 대해 데이터베이스를 기반으로 회귀 근사모델과 인공 신경망 근사모델을 생성하여 블레이드 동특성 요구도를 만족하는 구조설계를 수행하였다. 블레이드 동특성 근사모델을 구성하기 위한 데이터베이스 생성을 위하여 기존에 정의된 블레이드 구조 설계 절차를 기반으로 해석 절차를 구성하였다. 그리고 블레이드 단면 형상을 선정하고 단면 구성품인 스킨과 스파를 구현할 수 있는 인자를 단면 설계 변수로 선정하여 총 18개의 단면 설계 변수를 구성하였다. 이후, 실험계획법의 일환인 공간 채움 설계법을 활용하여 설계 변수 구속조건을 만족시키는 1000세트의 설계 변수 샘플을 생성하였다.
1000세트의 설계 변수 샘플값에 대해 회귀 근사 모델과 인공신경망 근사모델을 생성하였으며, 각 모델에 대한 분석을 통해 설계 변수에 대한 결과 영향도와 잔차의 분포 및 표준편차를 통해 근사모델의 신뢰성을 확인하였다. 이 후 두 근사모델에서 95.5 %의 확률로 동특성 요구도를 모두 만족시킬 수 있는 설계값을 도출하여 해석을 통해 설계 목표를 만족함을 확인하였으며, 각 근사모델에 대한 예측값들의 정확도 및 비교분석 결과 또한 확인하였다.
기 호 설 명
| Skint : | 블레이드 스킨 복합재 적충 수(ply) |
| Sparl : | 블레이드 코드 길이 대비 스파 길이(%) |
| Spart : | 블레이드 스파 복합재 적충 수(ply) |
| Rb : | 로터 시스템 반경(m) |
| rb : | 블레이드 단면 위치(m) |
| R2 : | 상관 계수 제곱 |
| σr : | 잔차의 표준편차 |
Acknowledgments
이 연구는 국방과학연구소의 지원(계약 번호 UC170032JD)으로 수행되었으며, 이에 감사드립니다.
References
-
Kim, T. J. and Cho, J. Y., 2018, Prop-blade Cross Section Design for QTP-UAV, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 46, No. 10, pp. 845~855.
[https://doi.org/10.5139/JKSAS.2018.46.10.845]

- Proust, M., 2021, JMP Documentation Library, SAS Campus Drive, Cary, NC 27513.
- Kang, Y. C., Cho, J. Y., Dhadwal, M. K., Jung, S. N. and Kim, T. J., 2011, Development of Program for Modeling of Cross Section of Composite Rotor Blade Using Open CASCADE, Proceedings of the KSAS Fall Conference, pp. 1787~1791.
-
Park, I. J., Jung, S. N., Cho, J. Y. and Kim, D. H., 2009, A Study on Calculation of Cross-section Properties for Composite Rotor Blade Using Finite Element Method, Journal of the Korean Society for Aeronautical and Space Sciences, Vol. 37, No. 5, pp. 442~449.
[https://doi.org/10.5139/JKSAS.2009.37.5.442]

- Johnson, W., 2007, CAMRAD II Comprehensive Analytical Model of Rotorcraft Aerodynamics and Dynamics. Volume I: Theory, Johnson Aeronautics, Palo Alto, CA.
- Eaton, J. W., Bateman, D., Hauberg, S. and Wehbring, R., 2019, GNU Octave Version 5.1.0 Manual: A High-level Interactive Language for Numerical Computations, https://www.gnu.org/software/octave/doc/v5.1.0, /.
- Adams, B. M., Bohnhoff, W. J., Dalbey, K. R., Ebeida, M. S., Eddy, J. P. et al., 2020, DAKOTA, a Multilevel Parallel Object-oriented Framework for Design Optimization, Parameter Estimation, Uncertainty Quantification, and Sensitivity Analysis: Version 6.12 User’s Manual, Sandia Technical Report SAND2020-12495, November.
- Proust, M., 2021, JMP Documentation Library: Design of Experiments Guide, SAS Campus Drive, Cary, NC.
- Proust, M., 2021, JMP Documentation Library: Fitting Linear Models, SAS Campus Drive, Cary, NC.
- Proust, M., 2021, JMP Documentation Library: Predictive and Specialized Modeling, SAS Campus Drive, Cary, NC.
- Montgomery, D. C. and Runger, G. C., 2014, Applied Statistics and Probability for Engineers - 6th Edition, Wiley, pp. 453~454.

Taejoo Kim received the M.S. and Ph.D. degrees in the Dept. of Aerospace engineering from Inha University in 2004 and 2020. He is a principal researcher in aeronautics research directorate of KARI. His research interests are helicopter rotor system composite blade and hub component structure design, analysis and test.

Seung-Kil Paek received the M.Sc. and Ph.D. degrees in the aerospace engineering from KAIST, Daejeon, Korea, in 1993 and 1998, respectively. Until 2006, he worked for T-50 supersonic jet trainer development as aeroelasticity engineer. Since then, he has been a principal researcher in the Aeronauctics Research Directorate of KARI and worked for Korean Helicopter Program. He is interested in flight vehicle aeroelasticity, active vibration control, model based system modeling and analysis, and multi-disciplinary analysis and optimization.

Jae Hyuk Lim received a B.S. degree in mechanical engineering from Inha University in 2000 and a Master and Ph.D. degree from KAIST in 2002 and 2006, respectively. He is currently an associate professor in the department of mechanical engineering at Jeonbuk National University. His research interests include attenuation of shock and vibration, multi-body dynamics, finite element methods, and machine learning applications.