원심진자 흡진기를 이용한 수력발전기 구동계 축소모델회전진동 저감 검토

1. 서 론

수력발전기 구동계는 다양한 회전 요소들로 구성되어 있으며 회전토크의 불균형에 의해 발생되는 다양한 형태의 회전진동이 발생된다^(1,2). 회전 모멘트는 물의 흐름과 발전기의 공극에서 발생하는 자기장에 의해 발생되는 자기 토크에 의해 발생된다⁽¹⁾. 한편으로는 물의 흐름 또는 작동 상황변화에 의한 랜덤 외란에 의해 랜덤 성분의 전자기 토크가 유발되며 다른 한편으로 물의 흐름, 기계적 토크, 전자기적 토크 등에 의해 발생되는 주기적인 외란도 다른 형태의 회전 진동을 발생시킨다. 평형을 이루어지지 않은 전자기력은 구동계에 횡방향 진동을 발생시킨다⁽²⁾. 수력발전기 구동계의 회전속도가 높지 않지만 회전진동과 횡방향 진동 또는 두 진동이 연성된 형태의 진동을 나타낸다. 따라서 구동계의 회전진동을 무시할 수 없다. 수력발전기의 시스템의 대형화에 따라 복잡한 수력 및 전자기력 가진이 두드러지게 된다^(1,2).

복잡한 시스템을 해석할 때 전체 시스템을 하위 구성 요소들로 나누고 각 하위 요소의 특성을 정의한 뒤 이들을 이용하여 전체의 시스템 특성을 파악하는 방법을 자주 사용한다. 하위 구성요소의 특성을 정의할 때 입력과 출력 사이의 관계를 주파수 함수로 정의하는 방법이 4단정수법이다. 이러한 접근 방법은 전체 시스템의 전달행렬을 하위 요소들의 전달행렬의 단순한 곱으로 나타낼 수 있다는 장점이 있다^(3~5).

회전 속도에 비례하는 주파수(목표 차수)에서 저감효과를 가지는 회전진동을 저감하기 위하여 원심진자흡진기(centrifugal pendulum absorber: CPA)가 다양한 형태로 회전시스템에 적용되고 있다^(6~10). 단순원심진자흡진기(simple CPA: SCPA)는 회전체의 중심으로부터 특정한 거리에 장착된 특정 길이의 암에 장착된 단순 진자를 이용한 CPA로 비교적 단순한 구조로 진동 저감 효과를 얻을 수 있다⁽⁹⁾.

이 연구에서는 수력발전기 구동계에서 발생하는 회전진동 저감을 위한 SCPA를 전달행렬법을 이용하여 검토한다. 구동계를 모사한 축소모델을 도입하고, 이에 대한 전달행렬을 유도한 다음 이론적인 해석과 상업용 소프트웨어를 이용한 해석으로 검증한다. 유도된 전달행렬과 이전 연구결과를 종합하여 SCPA를 장착한 축소모델의 전달행렬을 유도하고 이를 이용하여 SCPA 적용 시의 진동저감 효과를 검토한다. 아울러, 이 연구를 통하여 이전 연구에서 제시된 SCPA 전달행렬을 실제 시스템에 적용하여 실용성과 정확성을 추가 검증하고자 한다.

2. 수력발전기 축소 모델의 진동 분석

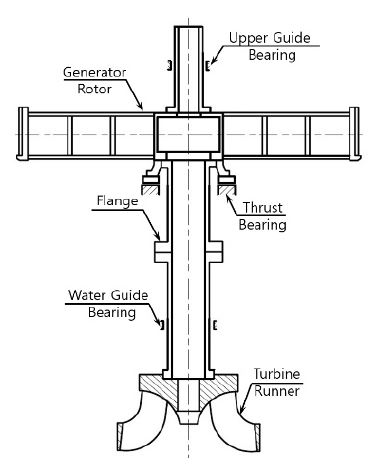
수력발전기 구동계는 발전기(generator) 및 터빈(turbine) 등 다양한 회전 요소들로 구성되어 있으며 이들 요소들의 특성이 전체 구동계의 회전 진동 특성을 결정한다⁽¹⁾. 이 연구의 대상인 수력발전기의 구동계는 Fig. 1에 설명되어있는 것과 같은 선행연구에서 분석되었던 시스템이다⁽²⁾.

Fig. 1

Schematic diagram of a reduced hydroelectric generator system

Fig. 1에서 보는 바와 같이, 구동계의 터빈에 가해지는 물의 흐름에 의해 발생된 회전토크가 축을 통해 전달되어 전체 시스템이 회전하게 된다. 또한, 앞 장에서 설명된 바와 같이 발전기에 작용하는 전자기 토크와 터빈에 작용하는 물의 가진력에 의해 다양한 회전진동이 발생한다.

2.1 수력발전기 축소 모델의 구성

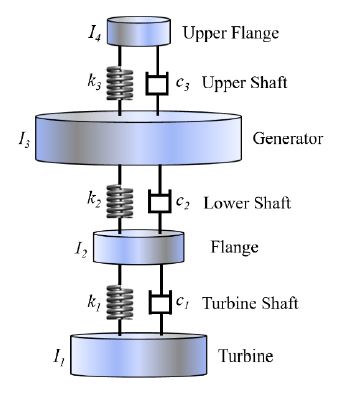
이 연구에서는 수력발전기 구동계의 동특성 분석과 추후 연구에서 예정된 검증 실험을 용이하게 하기 위하여 대상 구동계를 약 1/10 비율로 축소한 축소모델을 사용하여 수력발전기의 회전진동을 분석한다. 수력발전기 구동계 축소모델을 단순화한 이론적인 모델이 Fig. 2에 설명되어 있다.

Fig. 2

Theoretical simplification of the downsized drivetrain for hydroelectric generator

Fig. 2에서와 같이, 모델은 upper flange, generator, lower flange + turbine flange, turbine 등 4개의 관성요소를 가진 semi-definite 시스템으로 구성되었으며 각 관성요소는 회전축을 단순화한 강성(k) 및 감쇠(c) 요소로 연결되어 있다. Fig. 2의 단순화된 축소모델을 기준으로 시스템의 관성 및 강성 행렬을 유도하면 식 (1)과 같다.

$\[ \left[I\right]=\left[\begin{array}{cccc}{I}_1& 0& 0& 0\\ 0& I_2& 0& 0\\ 0& 0& I_3& 0\\ 0& 0& 0& I_4\end{array}\right] \]$

(1a)

$\[ \left[K\right]=\left[\begin{array}{cccc}{k}_1& -k_1& 0& 0\\ -k_1& k_1+k_2& -k_2& 0\\ 0& -k_2& k_2+k_3& -k_3\\ 0& 0& -k_3& k_3\end{array}\right] \]$

(1b)

감쇠 특성은 Rayleigh damping 가정에 따라서 계산하였다. 이 가정에 따라면 감쇠행렬은 식 (2)와 같이 관성 및 강성행렬로부터 유도할 수 있다.

$\[ \left[C\right]=\alpha \left[I\right]+\beta \left[K\right] \]$

(2)

여기서, α와 β는 각각 0.02 및 0.001로 적용하였다.

축소모델의 회전진동 특성이 원 시스템의 특성과 일치하도록 축소모델을 각 구성요소들의 기계적 특성을 선정하였다. Table 1에 원 시스템의 각 요소와 상당하는 축소 모델의 요소의 동특성이 비교, 설명되어 있다.

Table 1

Mechanical characteristics of the original and downsized drivetrain for hydroelectric generator

2.2 수력발전기 구동계 고유진동 특성

이 절에서는 Table 1에 나와 있는 기계적 특성을 가진 구동계의 원시스템과 축소모델에 대하여 관성 및 강성행렬을 이용한 이론적인 해석을 통하여 고유진동 특성을 파악한다. 이들 행렬을 이용하면 각 시스템의 고유진동 특성은 식 (3)을 이용하여 계산할 수 있다.

$\[ (-{\omega }^2[I]+[K\left]\right)\left\{\Theta \right\}=\left\{0\right\} \]$

(3)

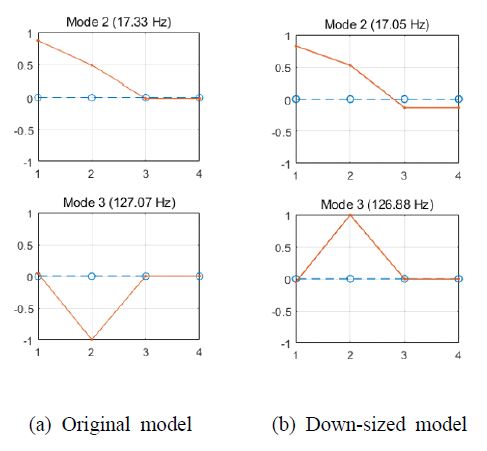
식 (3)에 설명되어있는 식을 이용하여 얻어진 두 모델의 고유진동 특성을 Fig. 3에 나타내었다.

Fig. 3

Modal characteristics of the drivetrain for the hydroelectric generator

Fig. 3에서 보는 바와 같이 두 모델은 모두 관심 주파수 영역 내에 17 Hz와 127 Hz 인근의 두 개의 고유진동수를 가지고 있으며 원시스템과 축소모델은 관심 주파수 영역에서의 고유진동수와 고유진동 모드가 모두 잘 일치하고 있음을 알 수 있다. 따라서, 앞에서 소개된 수력발전기 축소 모델을 기반으로 진동 특성을 분석한다.

3. 수력발전기 축소 모델의 진동 특성 분석

이 장에서는 앞에서 소개된 수력발전기 축소모델의 발전기와 터빈의 $$ \left|\dot{\omega }\right|/\left|T\right|$$를 전달행렬법을 적용하여 분석하고 그 결과를 1) 관성, 강성 및 감쇠 행렬 이용 방법, 2) 상업용 소프트웨어 simulation X 시뮬레이션 등을 이용하여 얻어진 결과와 비교함으로써 검증하였다.

이 연구에서는 수력발전기 구동계가 300 r/min의 명목속도(Ω)로 회전하고 있으며 터빈 부에는 식 (4)와 같은 명목 torque(T)와 조화함수 형태의 변동 torque(T_ν)가 작용한다고 가정한다.

선형 시스템으로 가정하면 각 요소에는 Ω와 함께 회전진동에 의한 조화함수 형태의 변동속도(ω_υi(t))가 동시에 발생된다고 가정할 수 있다(식 (5)).

이 연구의 목적이 구동계의 회전진동을 분석하고 저감하는 것임을 고려하여 아래 연구에서는 모델의 입력 토크 및 각 요소의 회전속도 중 시간에 따라 변동하는 성분에 집중하여 분석을 수행한다.

3.1 전달행렬법을 이용한 응답 특성

Fig. 2에 설명되어 있는 축소 모델은 Fig. 4와 같이 7개의 전달행렬을 이용하여 나타낼 수 있다. Fig. 4에 설명된 바와 같이 구동계를 구성하는 각 요소는 각각 하나의 전달행렬로 표시되었으며 전체 시스템의 전달행렬은 각 행렬을 연쇄적으로 곱하여 유도할 수 있다.

Fig. 4

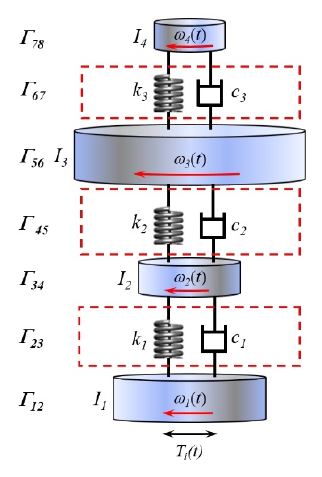
Transfer matrix representation of the down-sized model for the drivetrain of the hydroelectric generator

저자의 이전 연구⁽¹⁾와 Snowdon의 연구⁽²⁾에서의 관성 요소와 스프링 감쇠기의 전달행렬을 시스템의 기계적 특성을 이용하여 식 (6)과 같이 구할 수 있다.

$\[ {\Gamma }_{\left(2i-1\right)\left(2i\right)}=\left[\begin{array}{cc}1& i\omega I_i\\ 0& 1\end{array}\right] \]$

(6a)

$\[ {\Gamma }_{\left(2i\right)\left(2i+1\right)}=\left[\begin{array}{cc}1& 0\\ \frac{i\omega }{k_i+i\omega c_i}& 1\end{array}\right] \]$

(6b)

발전기의 accelerance($$ \left|\dot{{\omega }_3}\right|/\left|T_i\right|$$)는 driving point impedance 개념을 적용하여 식 (7)을 통하여 구할 수 있다.

$\[ {\Gamma }_{16}={\Gamma }_{12}{\Gamma }_{23}{\Gamma }_{34}{\Gamma }_{45}{\Gamma }_{56} \]$

(7a)

$\[ {\Gamma }_{68}={\Gamma }_{67}{\Gamma }_{78} \]$

(7b)

$\[ Z_{T_{16}}={\left({\Gamma }_{68}\right)}_{12}/{\left({\Gamma }_{68}\right)}_{22} \]$

(7c)

$\[ {TZ}_{16}=\frac{T_i}{{\omega }_3}={\left({\Gamma }_{16}\right)}_{11}{Z}_{T_{16}}+{\left({\Gamma }_{16}\right)}_{12} \]$

(7d)

$\[ \frac{1}{{TZ}_{16}}=\frac{{\omega }_3}{T_i}=\frac{1}{{\left({\Gamma }_{16}\right)}_{11}{Z}_{T_{16}}+{\left({\Gamma }_{16}\right)}_{12}} \]$

(7e)

$\[ \frac{{\dot{\omega }}_3}{T_i}=\frac{i\omega }{{\left({\Gamma }_{16}\right)}_{11}{Z}_{T_{16}}+{\left({\Gamma }_{16}\right)}_{12}} \]$

(7f)

터빈의 accelerance($$ \left|\dot{{\omega }_1}\right|/\left|T_i\right|$$)도 같은 방법을 적용하여 식 (8)과 같이 구할 수 있다.

$\[ {\Gamma }_{28}={\Gamma }_{23}{\Gamma }_{34}{\Gamma }_{45}{\Gamma }_{56}{\Gamma }_{67}{\Gamma }_{78} \]$

(8a)

$\[ Z_{T_{12}}={\left({\Gamma }_{28}\right)}_{12}/{\left({\Gamma }_{28}\right)}_{22} \]$

(8b)

$\[ {TZ}_{12}=\frac{T_i}{{\omega }_1}={\left({\Gamma }_{12}\right)}_{11}{Z}_{T_{12}}+{\left({\Gamma }_{12}\right)}_{12} \]$

(8c)

$\[ \frac{1}{{TZ}_{12}}=\frac{{\omega }_1}{T_i}=\frac{1}{{\left({\Gamma }_{12}\right)}_{11}{Z}_{T_{12}}+{\left({\Gamma }_{12}\right)}_{12}} \]$

(8d)

$\[ \frac{{\dot{\omega }}_1}{T_i}=\frac{i\omega }{{\left({\Gamma }_{12}\right)}_{11}{Z}_{T_{12}}+{\left({\Gamma }_{12}\right)}_{12}} \]$

(8e)

다음 절에서는 이렇게 구한 결과를 이론적인 해석 및 전한 시뮬레이션 결과를 이용하여 검증한다.

3.2 응답 특성 검증

첫 번째로 관성, 강성 및 감쇠 행렬을 이용한 이론적인 방법으로 축소 모델의 응답특성을 구하였다. 앞 장에서 설명한 바와 같이 감쇠 행렬(|C|)은 식 (2)를 이용하여 식 (9)와 같이 구할 수 있다.

$\[ \left[C\right]=\left[\begin{array}{cccc}{c}_1& -c_1& 0& 0\\ -c_1& c_1+c_2& -c_2& 0\\ 0& -c_2& c_2+c_3& -c_3\\ 0& 0& -c_3& c_3\end{array}\right] \]$

(9)

터빈에 조화함수 형태의 토크가 가해지는 경우 각 회전체에 발생되는 각 가속도는 다음 식으로 구할 수 있다.

$\[ \left\{\ddot{\Theta }\right\}=-{\omega }^2{\left(-{\omega }^2\left[I\right]+i\omega \left[C\right]+\left[K\right]\right)}^{-1}\left\{T\right\} \]$

(10)

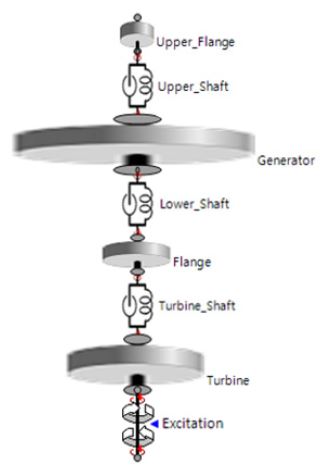
다음으로 상업용 software simulation X를 사용하여 축소 모델의 각가속도를 구하였다. Fig. 5에 축소 모델에 대한 simulation X 모델이 주어져 있다.

Fig. 5

Simulation X modeling of reduced hydroelectric generator

이 모델은 4개의 관성모멘트 요소를 3개의 스프링 감쇠기 요소로 연결한 구조이고 터빈에는 물의 흐름에 의한 가진 토크를 가할 수 있게 토크 요소를 연결하였다.

앞 절에서 소개한 전달행렬법을 이용하여 계산한 발전기와 터빈의 $$ \left|\dot{\omega }\right|/\left|T\right|$$를 위에서 언급한 이론적인 방법과 simulation X를 이용해 구한 결과와 Fig. 6에 비교하였다.

Fig. 6

ω˙/T of the generator and turbine in the down-sized model of the drivetrain (key: ◦ ◦ ◦: theoretical, ━: simulation X, ‑ ‑ ‑: TMM)

이론적인 방법과 전달행렬, 그리고 simulation X의 결과가 모두 잘 일치하는 것을 Fig. 6에서 확인할 수 있다. 따라서, 앞 절에서 정의된 구동계 축소모델에 대한 전달행렬들은 충분한 정확도를 가지고 있음을 확인할 수 있다.

4. 원심진자흡진기 적용

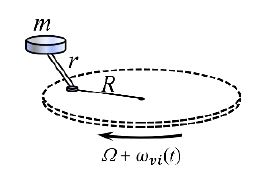
이전 연구에 따르면 수력발전기 구동계에 발생하는 회전진동은 다양한 차수(order) 성분을 포함한 가진토크에 의해 발생된다⁽¹⁾. 따라서, 실제 운전상태에서 구동계의 회전진동을 저감하기 위해서는 해당 차수 성분의 진동을 저감하는 것이 필요하다. 또한, 구동계의 회전수가 일정하게 유지되지 않으므로 회전수가 변동하는 경우에도 저감 효과를 유지할 수 있는 시스템이 필요하다. SCPA는 이러한 회전속도에 비례하는 주파수의 회전진동을 줄이는 데 효과적이다. SCPA에 대한 개략도가 Fig. 7에 주어져 있다.

Fig. 7

Schematics of a SCPA

Fig. 7에서 보는 것과 같이 SCPA는 중심에서 R만큼 떨어져 있는 부분에 피벗이 존재하고 이를 회전중심으로 반지름은 r인 Arm과 그 끝단에 달려있는 질량 m의 진자로 구성된다. SCPA는 진자 질량과 로터 중심과 피벗 사이 거리, 그리고 Arm의 길이에 의해 고유진동수가 정해지고 이는 식 (11)과 같다.

이 식에서 Ω는 로터의 명목 회전속도를 의미하고 CPA는 식 (11)에 주어진 ω_n주파수에서 진동 저감 효과를 가지므로 진동감쇠 효과가 회전속도에 비례하는 특징을 가진다는 것을 알 수 있다.

이전 연구에서 소개되었던 수력발전기 구동계에 작용하는 가진 토크를 감안하여 구동계 회전수의 1차 및 2차 진동을 저감하기 위하여 SCPA 적용을 검토한다. SCPA는 Fig. 2에 설명되어 있는 시스템의 고유진동 모드와 흡진기의 장착 편의성을 고려하여 구동계 flange 부에 장착하였다. 설계된 SCPA들의 제원을 Table 2에 정리하였다.

Table 2

Parameters of the 1st and 2nd order CPA system

4.1 전달행렬 모델

구동계 축소 모델에 SCPA를 적용하는 경우 예상되는 진동 저감 효과를 전달행렬법으로 검토하였다. SCPA가 적용된 축소 모델은 Fig. 8과 같이 전달행렬을 이용하여 표시할 수 있다.

Fig. 8

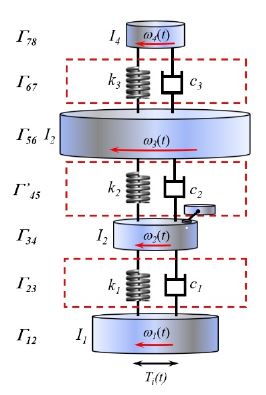
Transfer matrix representation of the down-sized model for the drivetrain of the hydroelectric generator with SCPA

SCPA가 적용된 축소모델의 전달행렬은 이전 연구를 통해 유도한 SCPA의 전달행렬을 이용하여 식 (6)에서 유도했던 축소모델 전달행렬을 수정함으로써 식 (12)와 같이 유도할 수 있다.

$\[ {\Gamma }_{\mathrm{c}\mathrm{p}\mathrm{a}}=\left[\begin{array}{cc}\frac{1+B}{B}& 0\\ \frac{1}{i\omega {mR}^{2}B\left(1+B\right)}& \frac{B}{1+B}\end{array}\right]\left[\begin{array}{cc}1& 0\\ k_{\mathrm{c}\mathrm{p}\mathrm{a}}^{\mathrm{*}}& 1\end{array}\right] \]$

(12a)

$\[ k_{\mathrm{c}\mathrm{p}\mathrm{a}}^{\mathrm{*}}=\frac{\mathrm{i}\omega }{{\mathrm{k}}_{\mathrm{c}\mathrm{p}\mathrm{a}}+\mathrm{i}\omega {\mathrm{c}}_{\mathrm{c}\mathrm{p}\mathrm{a}}} \]$

(12b)

$\[ Z_a={\left({\Gamma }_{\mathrm{c}\mathrm{p}\mathrm{a}}\right)}_{11}/{\left({\Gamma }_{\mathrm{c}\mathrm{p}\mathrm{a}}\right)}_{21} \]$

(12c)

$\[ {\Gamma }_{45}^{\text{'}}=\left[\begin{array}{cc}1& Z_a\\ 0& 1\end{array}\right]\left[\begin{array}{cc}1& Z_a\\ 0& 1\end{array}\right]{\Gamma }_{k2} \]$

(12d)

$\[ {\Gamma }_{k2}=\left[\begin{array}{cc}1& 0\\ \frac{1}{\left(\frac{k_2}{i\omega }+c_2\right)}& 1\end{array}\right] \]$

(12e)

식 (12)에서 K_cpa와 c_cpa는 SCPA의 강성과 감쇠를 나타내고, B는 SCPA의 거리비로 r/R을 나타낸다. K_cpa의 값은 mRrΩ² 이고 c_cpa는 Rayleigh 감쇠를 이용하여 구하였다⁽¹⁰⁾. 이렇게 정의된 전달행렬의 터빈에 회전 토크를 입력하고 응답을 구하는 요소에 해당하는 행렬에서 각가속도를 계산하여 accelerance를 구한다.

4.2 SCPA의 효과 분석

이 절에서는 Table 2에 설명된 두 종류의 SCPA를 적용했을 경우에 축소모델의 발전기와 터빈에 나타나는 FRF($$ \left|\dot{\omega }\right|/\left|T_i\right|$$)와 시간응답을 전달행렬법을 이용하여 구한 다음 SCPA를 적용하지 않았을 경우의 응답과 비교하여 SCPA의 효과를 분석하였다.

(1) FRF 비교

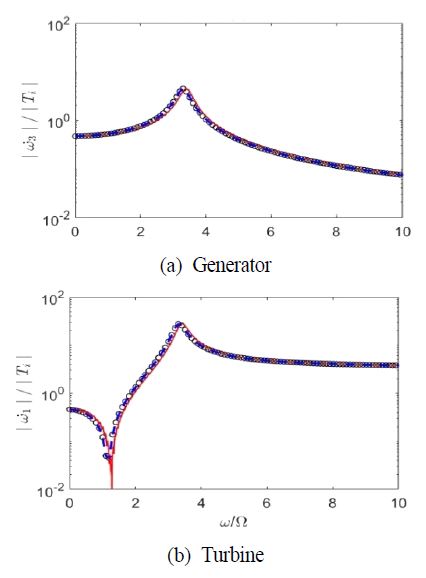
터빈에 가해지는 단위 조화가진에 의해 나타나는 발전기와 터빈의 $$ \left|\dot{\omega }\right|/\left|T_i\right|$$를 SCPA 적용 전, 후에 대한 전달행렬 모델을 이용하여 구한 다음 그 결과를 Fig. 9에 비교하였다.

Fig. 9

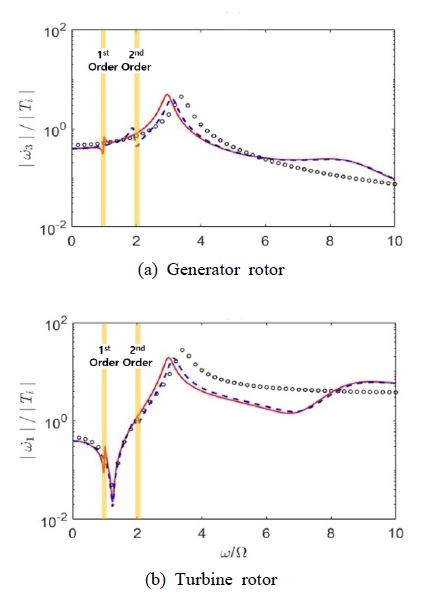
ω˙/T of downsized model of the drivetrain for hydro-generator system with CPA (key; ◦◦◦: original, ━: 1st order CPA, ‑ ‑ ‑: 2nd order CPA)

Fig. 9에서 보는 바와 같이 1차 및 2차 오더 성분의 회전 진동을 줄이기 위해 설계된 CPA를 부착한 수력발전기 축소모델 발전기의 각가속도가 황색으로 표시된 해당 오더 영역에서 충분한 진동 저감 효과를 나타내고 있음을 알 수 있다. 터빈의 경우 2차 오더 성분의 진동 저감 효과가 다소 적게 나타나지만 1차 오더 성분의 진동이 효과적으로 감쇠되는 것을 확인할 수 있다.

(2) 정상상태 시간 응답 비교

1차 오더와 2차 오더 성분의 회전 진동을 줄이기 위한 SCPA를 부착한 수력발전기 축소모델의 정상상태 시간응답을 전달행렬법을 이용하여 구한 다음, 원래 축소모델의 결과와 비교하여 진동 저감 효과를 확인하였다. 이 해석에서 사용된 입력은 터빈에 가해지는 식 (13)과 같은 조화입력은 경우에 대한 응답을 비교 검토하였다.

$\[ T\left(t\right)=\sin \left(2.32\pi t\right)+\sin \left(10\pi t\right)+\sin \left(20\pi t\right) \]$

(13)

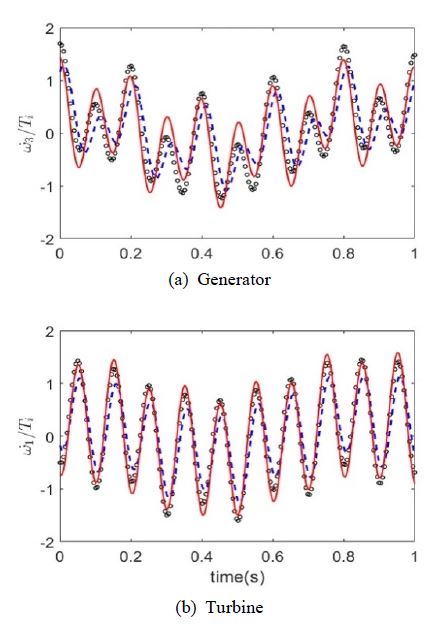
앞의 입력에 의해 세 종류 모델 내의 발전기 및 터빈에서 발생되는 정상상태 시간 응답을 Fig. 10에 비교하였다.

Fig. 10

Steady state analysis of CPA system (key; ◦◦◦: original, ━: 1st order CPA, ‑ ‑ ‑: 2nd order CPA)

Fig. 10에서 보는 바와 같이 SCPA가 적용됨에 따라 정상상태 시간응답에서도 비슷한 결과를 나타내는 것을 확인할 수 있다.

5. 결 론

수력발전기 구동계에서 발생하는 회전진동을 저감하기 위한 SCPA를 검토하였다. 첫 단계로 대상 구동계와 회전진동 특성이 일치하는 축소 모델을 도입하였다. 다음으로 축소모델의 조화응답 특성을 전달행렬법을 이용하여 검토한 다음 그 결과를 이론적인 해석과 컴퓨터 시뮬레이션을 통해 모델의 타당성을 검증하여 하였다.

다음으로 축소모델의 회전진동을 저감하기 위한 SCPA를 전달행렬법을 이용하여 검토하였다. 우선 구동계 축소모델의 1차 및 2차 회전진동을 저감하기 위한 SCPA의 제원을 검토하였다. 다음으로 이전 연구에서 소개된 SCPA의 전달행렬을 적용하여 축소모델에 대한 전달행렬을 수정한 다음 이를 이용하여 SCPA가 장착된 축소모델의 FRF와 시간응답을 계산하였다. 이 결과를 원래 모델의 응답과 비교하여 SCPA의 효과를 검토하였다. 결과에 따르면, 1차 오더 SCPA의 효과에 비해 2차 오더 SCPA의 효과가 더 우월한 것으로 나타났으며 발전기의 회전진동 저감 효과가 터빈의 효과에 비해 우월한 것으로 나타났다.

위의 결과를 종합해 볼 때, SCPA는 수력발전기 구동계의 회전진동을 저감하는데 충분한 효과를 가지고 있음을 알 수 있다. 또한 해당 시스템의 회전진동을 분석하는데 이전 연구에서 제시된 SCPA 전달행렬을 적용한 전달행렬법이 효과적임을 확인할 수 있다.

향후 연구에서는 이 연구에서 제시된 축소모델을 기준으로 제작된 실험장치를 이용한 실험을 통하여 이 연구 내용을 검증할 예정이다. 아울러, roll form type CPA등 다른 형태의 CPA system에 대한 전달행렬을 유도하고 이를 이용한 수력발전 구동계 회전진동 저감에 대한 연구도 진행할 예정이다.

Acknowledgments

이 논문는 한국수력원자력(주)에서 재원을 부담하여 경북대학교에서 수행한 연구결과입니다.

References

• Song, Z., Liu, Y., Guo, P. and Feng, J., 2018, Torsional Vibration Analysis of Hydro-generator Set Considered Electromagnetic and Hydraulic Vibration Resources Coupling, International Journal of Precision Engineering and Manufacturing, Vol. 19, No. 1, pp. 939~945. [https://doi.org/10.1007/s12541-018-0111-2]
• Si, X., Lu, W. and Chu, F., 2011, Lateral Vibration of Hydroelectric Generating Set with Different Supporting Condition of Thrust Pad, Shock and Vibration, Vol. 18, No. 1-2, pp. 317~331. [https://doi.org/10.1155/2011/867252]
• Snowdon, J. C., 1971, Mechanical Four-pole Parameters and Their Application, Journal of Sound and Vibration, Vol. 15, No. 3, pp. 307~323. [https://doi.org/10.1016/0022-460X(71)90427-5]
• Yun, J. H., Kwak, G. and Lee, H., 2019, Study on Performances of the Planetary Gear Type Anti-resonant Vibration Isolator Using Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 98~106. [https://doi.org/10.5050/KSNVE.2019.29.1.098]
• Yun, J. H. and Lee, H., 2018, Study on Performances of the Lever Type Anti-resonance Vibration Isolator Using Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 5, pp. 574~581. [https://doi.org/10.5050/KSNVE.2018.28.5.574]
• Taylor, E. S., 1936, Eliminating Crankshaft Torsional Vibration in Radial Aircraft Engines, SAE Journal, Vol. 38, No. 4, pp. 81~89. [https://doi.org/10.4271/360105]
• Denmant, H. H., 1992, Tautochronic Bifilar Pendulum Torsion Absorbers for Reciprocating Engines, Journal of Sound and Vibration, Vol. 159, No. 2, pp. 251~277. [https://doi.org/10.1016/0022-460X(92)90035-V]
• Shi, C., Parker, R. G. and Shaw, S. W., 2013, Tuning of Centrifugal Pendulum Vibration Absorbers for Translational and Rotational Vibration Reduction, Mechanism and Machine Theory, Vol. 66, pp. 56~65. [https://doi.org/10.1016/j.mechmachtheory.2013.03.004]
• Wedin, A., 2011, Reduction of Vibrations in Engines Using Centrifugal Pendulum Vibration Absorbers, Master’s Thesis in Automotive Engineering, Chalmers University of Technology.
• Kwak, G. and Lee, H., 2021, Investigation of the Point-mass Pendulum Centrifugal Pendulum Absorber Using Transfer Matrix Method, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 1, pp. 64~72. [https://doi.org/10.5050/KSNVE.2021.31.1.064]