교량 바닥판의 다중모드 진동 저감을 위한 2자유도 진동흡진기

1. 서 론

교량 구조물의 과도한 진동이나 처짐은 교량의 사용성을 저하시키고 구조물의 안전성에 문제를 야기하게 된다. 또한 반복적으로 작용하는 하중의 경우 포장면의 파손과 부재의 피로 문제를 발생시켜 보행자 및 차량 운전자에게 불안감을 느끼게 한다^(1~3). 따라서 교량 구조물의 진동을 저감시키기 위한 다양한 연구들이 수행되었다.

교량과 같은 대형 구조물에서는 가격이 저렴하고 간단한 수동 제어 장치인 진동흡진기에 대한 고려가 일반적이다. 진동흡진기의 기본적인 메커니즘은 진동흡진기의 공진주파수가 대상 구조물의 공진주파수에 인접하도록 하는 것이다^(4~6). 단자유도 형태의 진동흡진기는 차량 하중에 의한 교량의 진동에 대해 효과가 검증되었다. 그러나 풍하중에 의한 교량의 진동은 양력, 항력, 그리고 모멘트의 영향을 받기 때문에 다중모드를 가지게 되어 기존 진동흡진기로 효과적인 진동 저감이 어렵다. 다양한 모드의 진동 저감을 위해 Kwon⁽⁷⁾은 다중 단자유도 동조 질량 감쇠기 조합을 제안하고 상호 작용을 고려한 운동방정식을 도출하였다. Park 등⁽⁸⁾은 선형 및 회전자유도 진동흡진기를 복합적으로 사용하면 다중모드를 효율적으로 저감시킬 수 있음을 보였다. Zuo and Nayfeh⁽⁹⁾는 단일모드 제진을 위한 2자유도 진동흡진기를 제안하였으며 동일한 질량을 가지는 단자유도 진동흡진기에 비해 보다 뛰어난 성능을 가짐을 증명하였다.

나선(screw)은 Ball⁽¹⁰⁾에 의해 제안된 기하요소(entity)이다. Dimentberg⁽¹¹⁾는 나선을 이용하여 탄성적으로 지지된 단일강체의 운동방정식을 표현하였으며 Blanchet⁽¹²⁾은 나선이론을 이용해 표현한 연성된 다자유도 단일강체의 진동모드의 기하학적 의미를 규명하였다. Jang and Choi⁽¹³⁾는 두 개의 공간 진동체가 탄성체에 의해 직렬로 연결되어있는 경우 두 번째 물체가 다중모드 진동흡진기로 작동하는 조건을 연구하였다.

구조물의 다중 진동 모드를 기존 연구에서와 같이 복수의 진동흡진기 대신 단일 강체 2자유도 진동흡진기를 이용하여 제어할 수 있다면 보다 효율적인 다중모드 진동 저감이 가능하다. 이 연구에서는 나선이론을 이용하여 2개의 평면상의 강체로 구성된 진동계를 모델링한 후 다중 모드 제어를 위한 단일강체 2자유도 진동흡진기의 설계식을 제안하였다. 수치 예를 통해 풍하중의 영향을 받는 교량 바닥판이 갖는 2개의 모드를 제어할 수 있음을 보였다.

2. 설계 이론 및 수치 예

2.1 교량 바닥판의 강체 모델링

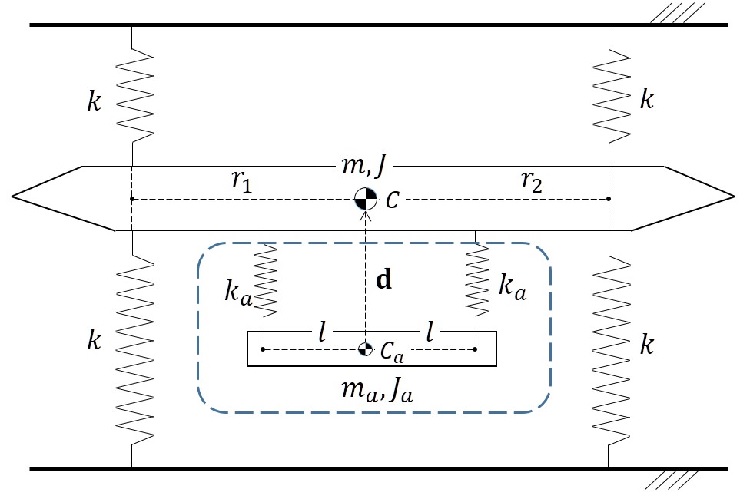
풍하중을 받는 구조물이 바람 방향 1차 모드 고유진동수가 1 Hz를 초과하거나 박스 내부의 단면 형상을 유지하기 위한 구조 부재가 적절히 설치된 경우에는 단면 비틀림에 대해 강체로 가정할 수 있다⁽¹⁴⁾. 따라서 풍하중을 받는 구조물에 대한 해석 및 실험에서 강체 모형을 많이 고려한다. Fig. 1은 Helgedagsrud 등⁽¹⁵⁾의 연구에서 제시된 교량바닥판의 동역학 모델을 나타내고 있다. 교량바닥판은 질량이 m이며 관성모멘트가 J 인 단일 강체로 모델링되었으며 교각과 바닥판을 연결하는 탄성체는 상하대칭 형태의 4개의 선형 스프링으로 모델링되었다. 선형 스프링들은 각각 무게중심으로부터의 거리가 r₁과 r₂인 지점에 위치해 있으며 강성은 모두 동일하게 k로 하였다. Fig. 1의 교량바닥판은 평면상에서 총 3개의 자유도를 갖게 되며 각 자유도의 운동은 서로 연성되어 있다. 기준점이 무게중심(C)과 일치할 경우 4개의 선형스프링들을 각각 선벡터(line vector)로 표현하여 구성한 자코비안 행렬은 식 (1)과 같다.

$\[ \mathbf{j}=\left[\begin{array}{cccc}0& 0& 0& 0\\ 1& 1& 1& 1\\ r_1& r_1& -r_2& -r_2\end{array}\right] \]$

(1)

Fig. 1

Modeling of the bridge deck with 2DOF tuned mass damper

식 (1)을 이용하여 미소 변위에 대한 강성행렬은 식 (2)와 같이 얻을 수 있다⁽¹⁶⁾.

$\[ {\mathbf{K}}_{\mathit{C}}=k{\mathbf{j}\mathbf{j}}^{\mathit{T}}=\left[\begin{array}{ccc}0& 0& 0\\ 0& 4k& 2k\left(r_1-r_2\right)\\ 0& 2k\left(r_1-r_2\right)& 2k\left(r_1^2+r_2^2\right)\end{array}\right] \]$

(2)

기준점에서 나타낸 관성행렬은 식 (3)과 같이 대각화된 형태로 나타낼 수 있다.

$\[ {\mathbf{M}}_{\mathit{C}}=\mathrm{diag}\left(m,m,J\right) \]$

(3)

교량바닥판이 Ω의 주파수로 미소 조화운동을 할 경우 변위는 식 (4)와 같이 나타낼 수 있다.

$\[ \mathbf{X}=\widehat{\mathbf{X}}{\mathrm{e}}^{j\mathrm{\Omega }t} \]$

(4)

여기서 $$ \widehat{\mathbf{X}}={\left[\begin{array}{lll}{\delta }_x,& {\delta }_y,& \varphi \end{array}\right]}^T$$이며 δ와 ϕ는 각각 선형 및 회전 변위의 크기를 의미한다. 식 (2)와 (3)의 강성, 관성행렬로부터 운동방정식을 구성하면 식 (5)를 얻을 수 있다.

$\[ \left({\mathbf{K}}_{\mathit{C}}-{\Omega }_i^2{\mathbf{M}}_{\mathit{C}}\right){\widehat{\mathbf{X}}}_{\mathit{i}}=0 \]$

(5)

식 (5)로부터 3개의 공진주파수 Ω_i와 공진모드 $$ {\widehat{\mathbf{X}}}_i$$를 얻을 수 있는데, 이중 강성행렬의 형태로 인해 1개의 강체 모드가 발생하므로 Fig. 1의 단일 강체 구조물은 2개의 공진주파수 및 공진 모드를 갖게 된다.

2.4 수치 예

Table 1은 교량바닥판 축소모형의 설계변수 및 진동 특성이다⁽¹⁵⁾. 축소모형은 5.0087 rad/s, 12.6351 rad/s의 2개의 공진주파수를 가지며 각각 수직병진 및 회전 모드를 나타낸다. 축소모형은 실스케일 모델과 공진주파수들의 비율이 일치되도록 설정되었다. Fig. 1과 같은 형태를 가지며 Table 1와 동일한 질량과 관성모멘트 및 진동주파수를 갖는 진동시스템은 Park and Jang⁽¹⁷⁾이 제안한 방법으로부터 Table 2와 같이 합성할 수 있다. 이 연구에서 제안하는 2자유도 진동흡진기는 Table 1의 공진주파수들을 식 (8)과 (17)에 따라 2자유도 진동흡진기의 2개의 공진주파수들과 각각 일치시켜 공진 모드를 소거할 수 있다. 진동흡진기의 질량과 교량바닥판 질량의 비율(μ)가 0.1이며 진동흡진기의 관성반경(ρ)이 56 mm이라고 할 때, 식 (8)로부터 진동흡진기의 설계변수들을 구하면 Table 3과 같다.

Table 1

Properties of small scale bridge deck

Table 2

Calculated properties of the bridge deck

Table 3

Properties of 2DOF vibration absorber

설계된 2자유도 진동흡진기의 성능을 평가하기 위해 모드 해석을 수행하였다. 전체 계에 대한 관성 및 강성행렬을 식 (18)과 같이 구할 수 있다.

$\[ {\stackrel{-}{\mathbf{M}}}_{\mathit{C}}=\left[\begin{array}{cc}{\mathbf{M}}_{\mathit{C}}& 0\\ 0& {\mathbf{K}}_{\mathit{C}}\end{array}\right],{\stackrel{-}{\mathbf{K}}}_{\mathit{C}}=\left[\begin{array}{cc}{\mathbf{K}}_{\mathit{C}}+{\mathbf{K}}_{\mathbf{C}}^{\mathit{a}}& -{\mathbf{K}}_{\mathbf{C}}^{\mathit{a}}\\ -{\mathbf{K}}_{\mathbf{C}}^{\mathit{a}}& {\mathbf{K}}_{\mathbf{C}}^{\mathit{a}}\end{array}\right] \]$

(18)

식 (18)의 행렬로부터 얻은 모드 벡터들의 행렬을 Ψ = [Φ Φ^a]^T라 할 때, 식 (19)를 이용해 주파수 응답을 구할 수 있다.

$\[ \left[\begin{array}{c}\widehat{\mathbf{X}}\\ {\widehat{\mathbf{X}}}^{\mathit{a}}\end{array}\right]=\sum _{r=1}^6\frac{{\left[\begin{array}{c}{\mathit{\Phi }}_{\mathit{r}}\\ {\mathit{\Phi }}_{\mathit{r}}^{\mathit{a}}\end{array}\right]}^T\left[\begin{array}{c}\widehat{\mathbf{W}}\\ 0\end{array}\right]\left[\begin{array}{c}{\mathit{\Phi }}_{\mathit{r}}\\ {\mathit{\Phi }}_{\mathit{r}}^{\mathit{a}}\end{array}\right]}{\left(1+j\beta \mathrm{\Omega }\right)k_r-{\Omega }^2{m}_r} \]$

(19)

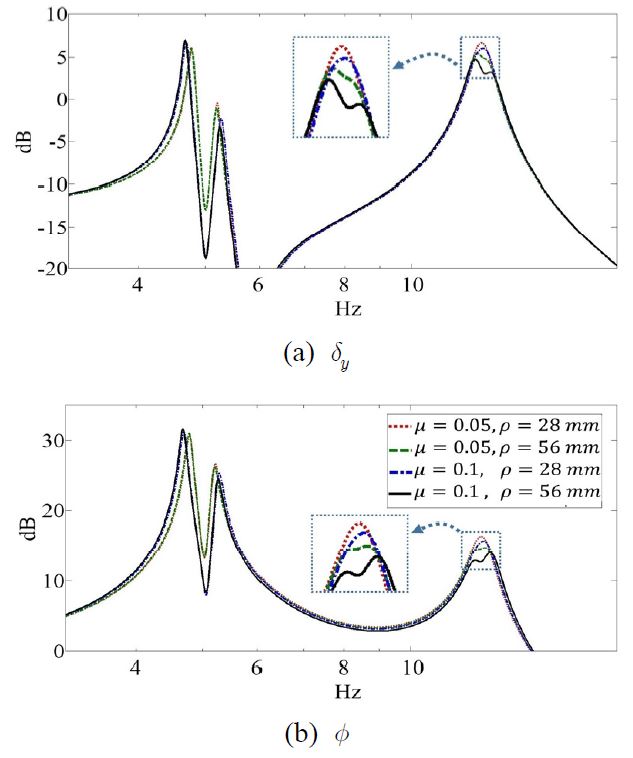
여기서 k_r, m_r은 각각 Ψ^TK_CΨ, Ψ^TM_CΨ의 r번째 원소이다. 또한 β는 비례감쇠계수이다. 식 (19)를 이용하여 구한 주파수 응답선도를 Fig. 2에 나타내었다. 녹색 점선은 진동흡진기를 적용하기 전 β=0.5 %인 경우의 응답이며 적색 파선은 진동흡진기를 적용한 경우의 비감쇠 응답을 나타낸다. 흑색 실선은 진동흡진기를 적용하고 β=0.5 %인 경우의 응답이다. 2자유도 진동흡진기에 의해 교량바닥판의 2개의 모드가 동시에 제어되는 것을 확인할 수 있다. 2자유도 진동흡진기의 성능은 기존의 단자유도 시스템과 달리 진동흡진기와 흡진 대상물체의 질량비(μ) 뿐만 아니라 진동흡진기의 관성반경(ρ)에도 영향을 받게 된다. Fig. 3은 질량비 및 관성반경을 각각 변경하였을 경우의 교량바닥판의 주파수 응답 특성을 나타내고 있다. 대체적으로 진동제어 성능은 질량비 및 관성반경이 커질수록 향상되는 것을 확인할 수 있다. 그러나 Fig. 3의 5 Hz 근처의 응답에서 볼 수 있듯이 질량비가 커질 때 오히려 일부 응답의 크기가 약간 증가하는 것을 관찰할 수 있는데 이것은 식 (17)에서 교량바닥판의 공진주파수와 2자유도 진동흡진기의 공진주파수가 정확히 일치하도록 설계하였기 때문인 것으로 보인다. 즉 제어하고자 하는 교량바닥판의 공진주파수와 2자유도 진동흡진기의 공진주파수 간의 약간의 차이가 있을 경우 보다 효율적인 제어가 가능할 수 있을 것으로 보이며 여기에 관한 최적화 연구를 추후 진행하고자 한다.

Fig. 2

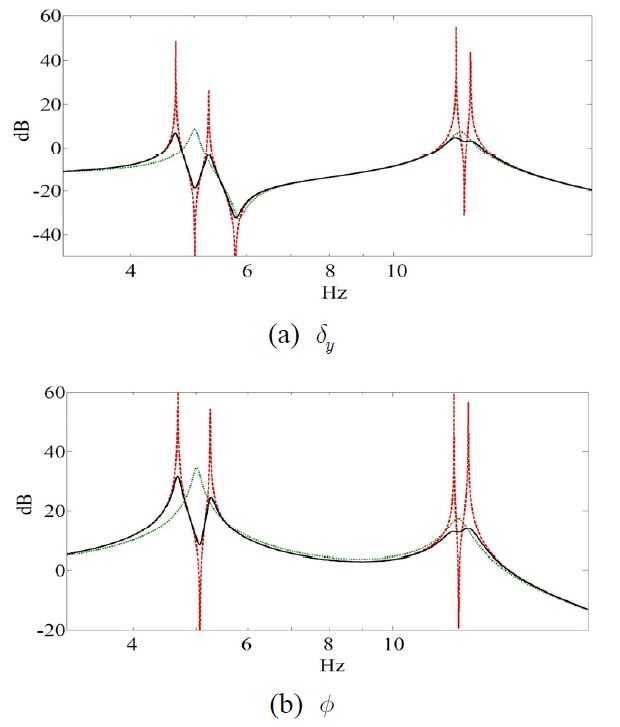
Frequency response of bridge deck without 2DOF absorber (green dotted), with 2DOF absorber (red dashed), and with damped absorber (black solid)

Fig. 3

Frequency response of bridge deck when μ=0.05 and ρ=28 mm (red dotted), μ=0.05 and ρ=56 mm (green dashed), μ=0.1 and ρ=28 mm (blue dash-dotted), and μ=0.1 and ρ=56 mm (black solid)

3. 결 론

이 연구에서는 풍하중의 영향을 받는 교량 바닥판의 다중모드 진동 저감을 위한 2자유도 진동흡진기의 설계 및 성능 검증 연구를 수행하였다. 2자유도 진동흡진기의 설계식을 제안하였으며 진동흡진기 적용 시 나타나는 교량바닥판 상사모델의 진동 특성을 수치 예를 통해 보였다. 그 결과 상사모델의 2개의 모드들을 제안된 2자유도 진동흡진기가 효과적으로 제어할 수 있음을 확인할 수 있었으며 단일 모드 진동흡진기 설계시 고려되는 질량비와 더불어 관성반경이 중요한 설계변수로 작용하는 것을 확인하였다.

Acknowledgments

이 논문은 2020학년도 군산대학교 신임교수 연구비 지원과 2022년도 정부(교육부)의 재원으로 한국연구재단의 지원을 받아 수행된 기초연구사업(NRF-2020R1I1A1A01073676)의 연구비 지원으로 수행되었습니다.

References

• Kim, N. S. and Jeon, B. G., 2007, Evaluation of Comport Limit on Bridge Vibration, Proceedings of the KSNVE Annual Spring Conference, pp. 161~170.
• Lee, H. S., Ha, S. Y., Hwang, I. H. and Lee, J. S., 2010, A Study on Modeling for Vibration Serviceability Evaluation, Proceedings of the Computational Structural Engineering Institute Conference, pp. 39~42.
• Jeon, G. H., Kim, S. H., Lee, J. H., Lee, S. W., Heo, J. Y., Lee, Y. S. et al., 2000, Development of Evaluation Procedures for Vibration and Displacement Serviceability of Bridges, Final Report TRKO201100007262.
• Kwon, H. C., Kim, M. C. and Lee, I. W., 1998, Vibration Control of Bridges under Moving Loads, Computers & Structures, Vol. 66, No. 4, pp. 473~480. [https://doi.org/10.1016/S0045-7949(97)00087-4]
• Nam, H., Fujino, Y. and Warnitchai P., 2008, Optimal Tuned Mass Damper for Seismic Applications and Practical Design Formulars, Engineering Structures, Vol. 30, No. 3, pp. 707~715. [https://doi.org/10.1016/j.engstruct.2007.05.007]
• Kim, H. T., Cho, N. S. and Seo, J. W., 2010, Experimental Evaluation of Tuned Mass Damper Performance, Proceedings of the KSNVE Annual Spring Conference, pp. 668~669.
• Kwon, S. D., 1998, Effectiveness of TMDs for Control of Traffic Induced Bridge Vibrations, Journal of the Korean Society of Civil Engineers, Vol. 18, No. 1-4, pp. 457~467.
• Park, S. G., Lee, S. B. and Choi, J. H., 2019, Plate Vibration Suppression with Translational and Rotational Dynamic Vibration Absorbers, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 21~29. [https://doi.org/10.5050/KSNVE.2019.29.1.021]
• Zuo, L. and Nayfeh, S. A., 2006, The Two-degree-of-freedom Tuned-mass Damper for Suppression of Single-mode Vibration under Random and Harmonic Excitation, Journal of Vibration and Acoustics, Vol. 128, No. 1, pp. 56~65. [https://doi.org/10.1115/1.2128639]
• Ball, R. S., 1900, The Theory of Screws, Dublin: Hodges, Foster.
• Dimentberg, F. M., 1965, The Screw Calculus and Its Application in Mechanics, Foreign Technology Division, Wright-Patterson Air Force Base, Ohio, Document No. FTD-HT_23-1632-67.
• Blanchet, P., 1998, Linear Vibration Analysis Using Screw Theory, Doctoral Dissertation, Georgia Institute of Technology, Atlanta, US.
• Jang, S. J. and Choi, Y. J., 2007, Geometrical Design Method of Multi-degree-of-freedom Dynamic Vibration Absorbers, Journal of Sound and Vibration, Vol. 303, No. 1-2, pp. 343-356. [https://doi.org/10.1016/j.jsv.2007.01.017]
• Ministry of Land, Infrastructure and Transport, 2016, Korea Highway Bridge Design Code (Limit State Design), Sejong: MOLIT.
• Helgedagsrud, T. A., Bazilevs, Y., Mathisen, K. M. and Øiseth, O. A., 2019, Computational and Experimental Investigation of Free Vibration and Flutter of Bridge Decks, Computational Mechanics, Vol. 63, No. 1, pp. 121~136. [https://doi.org/10.1007/s00466-018-1587-4]
• Griffis, M. and Duffy, J., 1991, Kinestatic Control: A Novel Theory for Simultaneously Regulating Force and Displacement, Journal of Mechanical Design, Vol. 113, No. 4, pp. 508~515. [https://doi.org/10.1115/1.2912812]
• Park, S. B. and Jang, S. J., 2020, Design Method for the 2DOF Electromagnetic Vibrational Energy Harvester, Smart Structures and Systems, Vol. 25, No. 4, pp. 393~399.