임팩트 해머 실험에 의한 주파수 응답 함수를 구함에 있어서 최적 데이터 세트를 구성하기 위한 MS 유사성 함수의 응용
© The Korean Society for Noise and Vibration Engineering
Abstract
Impact hammer testing is the most frequently used and widely adopted method for estimating the frequency response function (FRF). It requires averaging several impact test data to minimize random error. This method requires constant excitation conditions (excitation point, angle, duration, etc.) to be maintained when striking the impact hammer onto a structure. Consequently, choosing the set of data with the same excitation conditions among multiple repeated experimental data is important to obtain the best possible FRF, especially when commercial software is unavailable. In this paper, a method of selecting the optimal impact data set has been proposed using the recently developed the magnitude and shpae (MS) similarity function. The results show that the proposed method estimated the FRF of a structure efficiently with high coherence values.
Keywords:
Impact Hammer Test, Frequency Response Function, MS Similarity Function, Coherence Function키워드:
임팩트 해머 실험, 주파수 응답 함수, MS 유사성 함수, 기여도 함수1. 서 론
실험적으로 구한 주파수 응답 함수(frequency response function, FRF)는 구조물의 안정성 평가 또는 상태진단 등 다양한 목적을 위한 진동 특성의 분석에 있어서 매우 중요하다. 그러나 실험 과정에서는 오차가 발생할 수 있는 요인이 많이 있으며, 특히 실험적 모드 해석과 같은 많은 FRF가 사용되는 경우에는 오차가 누적되어 해석상의 오류가 발생될 수 있다. 따라서 과거로부터 양질의 FRF를 취득하기 위한 많은 연구가 수행되어 왔으며(1~7), FRF의 편향오차(bias error)와 누설오차(leakage error)를 줄이거나 창함수(window function)과 FRF 추정식(estimator)를 개선하는 등의 다양한 신호처리 방법들은 현재 상용화되어 보편적인 방법으로 사용되고 있다.
실험적으로 FRF를 구할 때, 일반적으로 가진기(shaker)를 이용하거나 임팩트 해머(impact hammer)를 이용하여 구조물을 가진하는데, 임팩트 해머를 이용한 가진 방법이 비교적 간단하고 편리하기 때문에 많이 이용되고 있다. 그러나 임팩트 해머 실험의 경우에는 가진기를 사용하는 경우보다 더 많은 실험적 오차가 발생할 수 있다. 예로서, 임팩트 실험을 이용하여 FRF를 구할 때 누설오차는 가진기를 사용할 때 보다 더 크게 발생할 수 있으며(4,5), 임펄스의 지속시간이 긴 경우 주파수 상의 신뢰 구간이 줄어들 수 있다(8).
최근에는 이러한 임팩트 해머 실험에서 발생할 수 있는 실험적 오차를 줄이기 위하여 해머 팁(tip)의 선정과 가속도계 부착 위치 선정 등 실험적 방법과 지수창 함수의 계수 설정 등과 같은 계측기의 설정 방법을 제시하고 있으나(9), 임팩트 해머 실험에서 발생하는 실험적 오차의 근본적인 원인에 대한 해결책은 되지 못하는 실정이다.
즉, 임팩트 해머를 이용한 방법으로 FRF를 구할 때 랜덤오차(random error)를 줄이기 위해서 약 5회 정도의 반복된 실험 데이터를 주파수 영역에서 평균해야 하는데(10), 이때 동일한 가진 위치와 동일한 가진 각도를 유지하는 것이 매우 중요하다(11). 그러나, 보통 손으로 가진하는 실험의 특성상 이를 유지하는 것은 매우 어렵고, 가진을 위한 특별한 지그(jig)를 제작하는 것도 어려운 경우가 많다.
반복적인 임팩트 해머 실험 과정에서 동일한 조건(가진 위치와 각도)를 유지하지 못하면 최종적으로 구한 FRF의 기여도 함수(coherence function)값은 낮아지게 되어 FRF의 신뢰도는 떨어지게 된다. 따라서 평균에 사용되어지는 데이터의 신뢰성을 확보하기 위하여 기여도 함수가 일반적으로 많이 사용되고 있다. 일반적으로 상용 소프트웨어를 이용한 임팩트 해머 실험에서는 최초로 취득한 데이터를 기준으로 삼고 연속해서 데이터를 취득할 때마다 FRF와 기여도 함수를 계산하여 1에 가까우면 채택(accept)하고 그렇지 않으면 폐기(reject)하여 다시 데이터를 취득하는 방식을 사용한다. 이러한 채택/폐기 알고리즘은 데이터를 취득하는 동시에 기여도 함수와 FRF를 구할 수 있는 편리함이 있지만, 기준으로 삼는 최초로 취득한 데이터가 좋지 않을 때는 재실험을 해야 하는 번거로움이 있다. 또한, 이러한 알고리즘이 포함된 상용 소프트웨어는 고가의 경우가 많아 장비가 구축되지 않는 환경에서 사용이 제한된다.
이러한 단점을 극복하기 위하여 Brandt 등(12)은 먼저 많은 샘플 데이터를 취득한 다음, 오프라인 또는 후처리(post processing) 방법을 이용하여 기여도 함수가 높게 나오는 데이터 세트를 선별하는 방법을 제안하였다. 이 연구에서 사용된 후처리 방법은 취득한 모든 샘플 데이터를 대상으로 조합이 가능한 데이터 세트에 대한 기여도 함수를 직접 계산하는 알고리즘을 제시하고 있는데, 취득한 데이터가 많을수록 경우의 수는 기하급수적으로 늘어나는 단점이 있다. 예로서 10개의 샘플 데이터 중 최적의 데이터 5개를 선별할 때 총 252가지의 데이터 세트를 고려해야 한다. 또한, 기여도 함수를 계산하기 위해서는 파워 스펙트럼(power spectrum)과 상호 스펙트럼(cross-spectrum)을 먼저 구해야 하므로 다소 복잡한 과정을 거치게 된다.
이 논문에서는 최근 개발된 MS 유사성 함수(magnitude and shape similarity function)를(13) 이용하여 기여도 함수를 직접 이용하는 알고리즘의 단점을 보완하며 고가의 상용 소프트웨어가 없는 경우에도 비교적 쉽게 최적의 데이터 세트를 선별하는 방법을 제안하고자 한다. 이 방법의 효과성을 검증하기 위하여 외팔보를 이용한 실험 데이터를 취득한 다음, MS 유사성 함수를 이용하여 선별된 최적의 데이터 세트에 대한 FRF와 기여도 함수를 함께 비교하였다.
2. 가상 FRF와 MS 유사성 함수
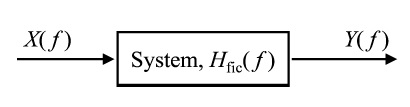
MS 유사성 함수는 가상 FRF라는 개념에 기초를 두고 있는데, 가상 FRF는 Fig. 1과 같이 주파수 영역에서 임의의 두 신호 X(f)와 Y(f)사이에 가상의 입력-출력 관계를 나타내는 주파수 응답 함수, Hfic(f)를 구성하여 X(f)와 Y(f)의 차이점을 분석하는 방법으로서 Shin 등(14)에 의해서 처음으로 소개되었다. 식 (1)과 식 (2)로 표현되어 진다.
Fig. 1에 나타낸 두 신호 X(f)와 Y(f)를 크기와 위상으로 구분하여 나타내면 식 (1)과 같으며, 가상 FRF의 크기와 위상은 각각 식 (2)로 표현될 수 있다.
| (1) |
| (2) |
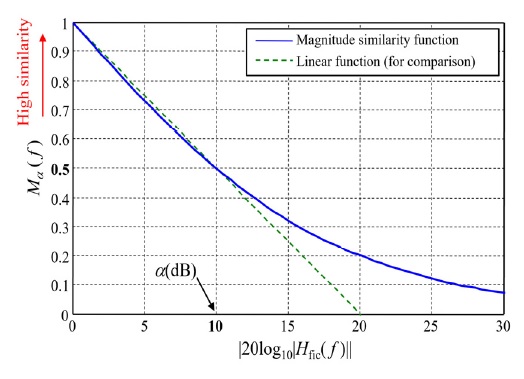
여기서, 가상 FRF의 크기 |Hfic(f)|는 X(f)와 Y(f)의 크기 관계를 직접적으로 나타내고 있으며, 위상 차이를 나타내는 argHfic(f)는 두 신호의 모양 관계를 간접적으로 나타내고 있으며, 이를 바탕으로 Shin(13)은 크기 유사성 함수(magnitude similarity function), Mα(f)와 모양 유사성 함수(shape similarity function), Sβ(f)를 식 (3)과 식 (4)와 같이 정의하였다.
| (3) |
| (4) |
Mα(f)와 Sβ(f)는 주파수 함수로서 0 ~ 1 사이의 값을 가지며 두 신호 X(f)와 Y(f)의 유사성이 클수록 1에 가까운 값을 갖는데, 특정 주파수 f에서 두 신호 X(f)와 Y(f)의 크기가 같은 경우에 크기 유사성 함수 Mα(f)는 1의 값을 가지고, α(dB) 차이가 날 때는 0.5의 값을 가지며 차이가 클수록 0에 가까운 값을 가진다. 예를 들면, α=10 dB인 경우에 대해서 두 신호의 크기 비를 dB로 나타낸 |20log10|Hfic(f)||와 Mα(f)의 관계를 Fig. 2에 나타내었다. Fig. 2에서 보듯이, |20log10|Hfic(f)||와 Mα(f)는 비선형적인 관계를 나타내지만 α(dB)까지, 즉 Mα(f)의 값이 0.5 ~ 1의 범위에서는 비교적 선형적인 관계를 나타내고 있다. 이러한 특성을 이용하여, 두 신호의 주파수별 크기 유사성을 정량적으로 나타낼 수 있다.
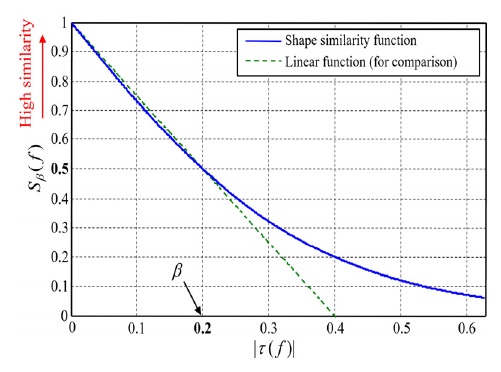
모양 유사성 함수 Sβ(f)는 가상 FRF의 위상을 미분하여 구한 그룹지연(group delay)을 이용하여, 두 신호 X(f)와 Y(f)에 상응하는 시간 영역에서의 신호 x(t)와 y(t)의 모양 차이를 나타내고 있다. 두 신호의 모양 차이와 그룹지연과의 관계는 13번째 참고문헌에 자세히 기술되어 있는데, 크기 유사성 함수와는 달리 ‘모양’이라는 정성적인 특성을 다루고 있기 때문에 여러 신호의 모양을 상대적으로 비교할 때 사용할 수 있다. 그룹지연 τ(f)과 Sβ(f)의 관계를 β=0.2인 경우에 대해서 Fig. 3에 나타내었으며, 크기 유사성 함수와 마찬가지로 |τ(f)|=β까지, 즉 Sβ(f)의 값이 0.5 ~ 1의 범위에서는 비교적 선형적인 관계를 나타내고 있음을 알 수 있다.
MS 유사성 함수는 Mα(f)와 Sβ(f)에 가중치를 부여하여 식 (5)와 같이 두 함수의 합으로 정의되는데, 가중치는 신호의 특성과 적용 대상에 따라서 적절하게 부여하며 가중치의 합은 1이 되도록 한다.
| (5) |
식 (3) ~ 식 (5)는 주파수 함수로서 주파수별 유사성을 분석할 때 유용하게 사용될 수 있으며, 식 (5) ~ 식 (6)과 같이 관심 주파수 구간(f1~f2)의 값을 평균한 MS 유사성 지수(index)를 이용하여 유사성 정도를 한 개의 수치로 나타내어 이용할 수도 있다.
| (6) |
| (7) |
이 논문에서 다루고자 하는, 양질의 FRF를 구하기 위한 최적 데이터 세트를 선정함에 있어서 식 (5)의 가중치 설정도 중요하다. 임팩트 해머 실험에서 실험적 오차가 발생할 수 있는 가장 큰 요인은 가진 각도와 가진 위치를 항상 동일하게 유지할 수 없는 점이다. 일반적으로 가진 각도에 따라서 FRF의 크기가 달라지며, 가진 위치에 따라서는 FRF의 크기와 위상 모두 달라질 수 있다. 그러나, 가진 위치가 미세하게 다른 경우는 FRF의 위상 차이는 거의 일어나지 않는다. 예로서, 참고문헌 15번에서 다룬 이론적 외팔보 모델에 대해서 가진 위치를 2 mm 차이를 두고 구한 FRF의 크기와 위상을 Fig. 4에 나타내었는데(15), FRF의 크기 변화는 명확하게 나타나지만 위상의 변화는 거의 없는 것을 알 수 있다.
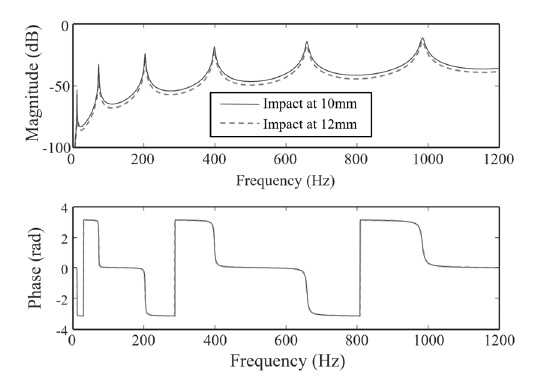
Comparison of magnitude and phase spectrum for the case of neighboring impacts using the mathematical cantilever beam model
또한, 모양 유사성 함수를 구하기 위해서는 식 (4)에 나타낸 것과 같이 그룹지연을 구하기 위한 미분 과정이 필요한 데 실험 데이터를 수치적으로 미분할 때 오차가 추가적으로 발생할 수 있다. 따라서, 이 논문에서는 가진 조건에 따른 FRF의 변화를 최소화할 수 있는 데이터 세트를 선정하는 것이 목적이기 때문에 크기 유사성 함수 Mα(f)만 이용하는 것이 더 효과적이다. 이는 MS 유사성 함수를 적용할 때 물리적 특성에 따라 Mα(f)와 Sβ(f)를 선별하여 사용하거나 식 (5)의 가중치를 적절히 적용해야 함을 보여주는데, 예로서 LTM(location template matching) 방법에(14,15) 적용할 때는 크기 유사성 함수는 고려하지 않고 모양 유사성 함수만 고려해야 한다.
3. 실험적 검증 및 결과
3.1 실험 장치 및 MS 유사성 함수의 적용 방법
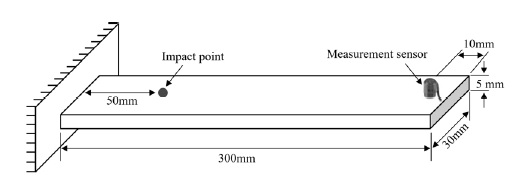
실험 대상으로 Fig. 5와 같은 300 mm × 30 mm × 5 mm 크기의 강(steel) 재질의 외팔보를 사용하였으며, 가속도 센서를 외팔보의 끝 단에서 10 mm 떨어진 곳에 부착하고 임팩트 해머의 가진 위치는 고정단에서 50 mm 떨어진 표시된 위치로 설정하여, 총 10개의 입력-출력 데이터를 취득한 다음 각각의 입력-출력 신호를 바탕으로 평균하지 않은 10개의 샘플 를 구하였다. 이때 손으로 임팩트 해머를 이용하였기 때문에 임팩트 해머의 가진 위치와 각도는 완벽히 동일하게 유지하지 못하였다. 따라서 샘플 FRF간의 차이가 발생할 수밖에 없으며, 이 논문에서는 샘플 FRF간의 크기 유사성 함수 Mα(f)를 비교하여 유사성이 가장 높은 5개의 샘플 FRF에 해당되는 입력-출력 데이터 세트를 이용하여 최적 FRF를 구하였다.
3.2 샘플 FRF 간의 MS 유사성 함수 비교
이 절에서는 샘플 FRF 사이의 유사성 함수가 어떻게 나타나는지에 대한 예를 기술하고자 한다. 모든 샘플 FRF를 비교한 결과, 크기 유사성이 가장 높은 쌍은 과 이고 유사성이 가장 낮은 쌍은 과 로 파악되었으며 Fig. 6과 Fig. 7에 각 쌍의 샘플 주파수 응답 함수와 크기 유사성 함수 Mα(f)를 나타내었다. 이때 크기 유사성 함수의 계수는 α=5 dB로 하여 계산하였는데, 상대적으로 유사성이 높고 낮음을 파악하면 되기 때문에 α값의 설정은 크게 중요하지 않다.
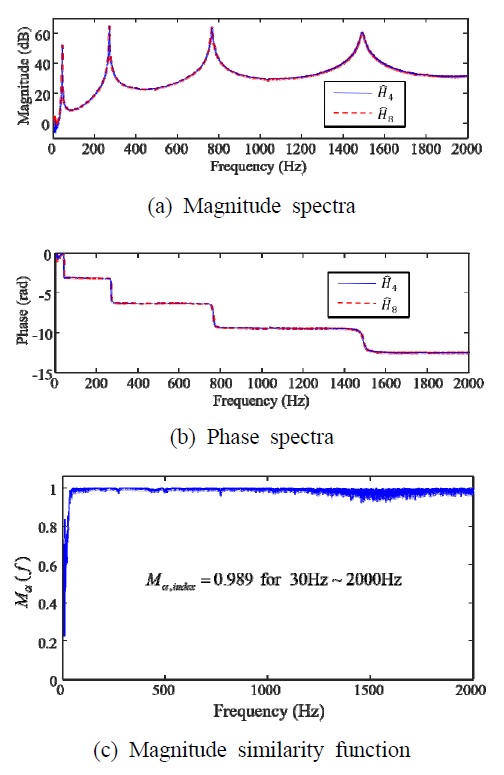
Sample FRFs(Hˆ4 & Hˆ8) and the corresponding magnitude similarity function (Mα, index= 0.989 for 30 Hz ~ 2000 Hz)
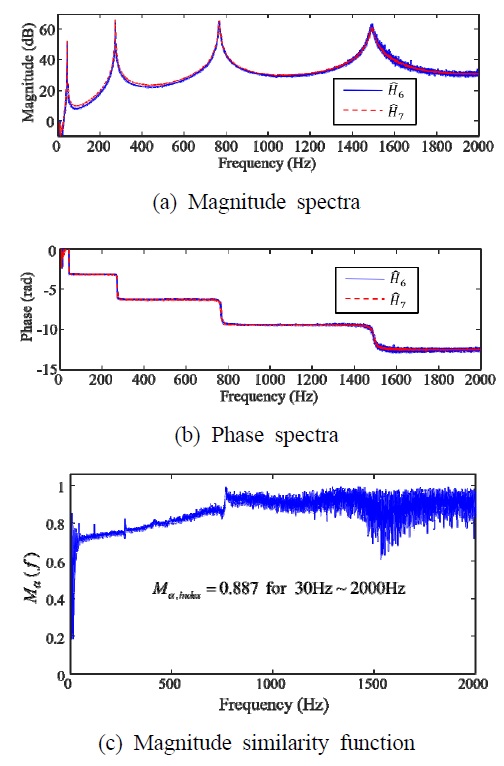
Sample FRFs(Hˆ6 & Hˆ7) and the corresponding magnitude similarity function (Mα, index= 0.887 for 30 Hz ~ 2000 Hz)
Fig. 6과 Fig. 7에 나타낸 두 샘플 FRF 쌍의 크기 유사성 함수를 비교하면, 과 사이의 크기 유사성 함수는 신호 대 잡음비(signal-to-noise ratio)가 낮은 약 30 Hz 이하의 성분을 제외한 전 주파수 영역에서 1에 가까운 값을 나타내고 있으며, 과 사이의 크기 유사성은 상대적으로 매우 낮은 값을 나타내고 있음을 알 수 있다.
샘플 FRF 사이의 유사성을 보다 정량적으로 나타내기 위해서 관심 주파수 대역을 30 Hz ~ 2000 Hz로 설정하고 식 (6)을 이용하여 크기 유사성 지수(Mα, index)를 계산한 결과 과 사이는 0.989, 과 사이는 0.887로 파악되었으며, 이는 유사성 지수를 이용하면 관심 주파수 대역에 대해서 샘플 FRF 사이의 상대적인 유사성을 잘 구분할 수 있음을 나타내고 있다.
3.3 최적 데이터 세트 선정 및 FRF의 질적 검증
앞 절에서와 같은 방법으로 모든 샘플 FRF 사이의 크기 유사성 지수를 계산하여 10×10 행렬 형태로 구성하여 Table 1에 나타내었다. 표를 구성할 때, 열(column)에 나타낸 각 샘플 를 기준으로 행(row)에 나타낸 각각의 샘플 FRF와의 유사성 지수를 나타내었으며 대칭적인 구조를 가지기 때문에 실제 필요한 유사성 지수는 총 45개이다. Table 1의 가장 아래 부분에 표시한 값들은 각각의 열에서 1을 제외한 가장 큰 4개의 합과 가장 작은 4개의 합을 표시하였다. Table 1에서 또는 을 기준으로 할 때 가장 큰 4개 유사성 지수의 합이 최대가 되는 것을 알 수 있으며, 이를 바탕으로 샘플 FRF 사이의 유사성이 가장 큰 5개를 선택하고자 하는 경우, 최적의 데이터 세트는 로 구성될 수 있음을 알 수 있다(Table 1에 볼드체로 표시). 비교를 위하여, 유사한 방법으로 가장 좋지 않은 데이터 세트는 로 구성될 수 있다(Table 1에 밑줄로 표시).
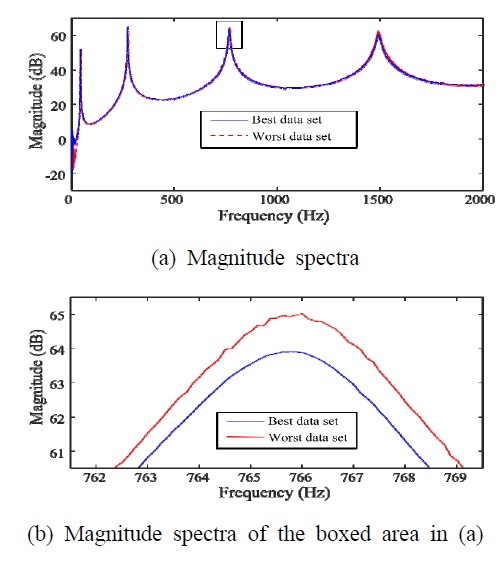
선별된 최적 입력-출력 데이터 세트(1, 3, 4, 5, 8)와 가장 좋지 않은 데이터 세트(1, 6, 7, 9, 10) 각각을 이용한 FRF와 기여도 함수(coherence function)를 Fig. 8과 Fig. 9에 각각 나타내었다. 두 경우를 비교하면, 최적 데이터 세트의 경우 관심주파수 대역(30 Hz ~ 2000 Hz) 전 영역에서 기여도 함숫값이 거의 1을 유지하고 있음을 알 수 있는 반면에 가장 좋지 않은 데이터 세트의 경우 고주파 영역에서의 기여도 함숫값이 현저히 떨어지는 것을 확인할 수 있다.
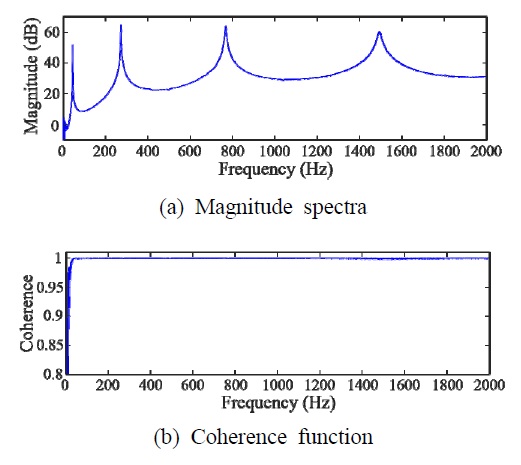
FRF using the best data set (1,3,4,5,8) and the corresponding coherence function (average value is 0.9998)
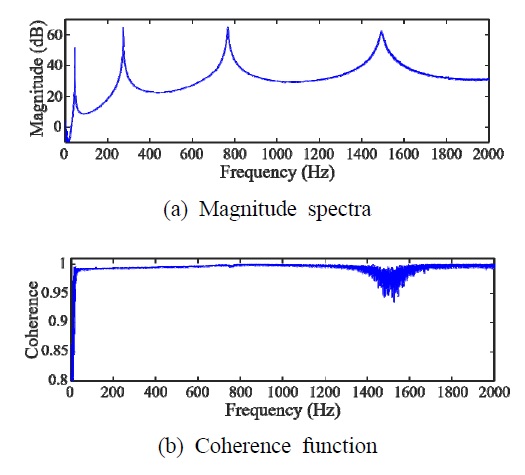
FRF using the worst data set (1,6,7,9,10) and the corresponding coherence function (average value is 0.9947)
또한, 신호 대 잡음비가 높은 고유진동수에서의 기여도 함숫값을 Table 2에 나타내었는데, 최적 데이터 세트를 사용한 경우가 상대적으로 매우 좋은 것을 알 수 있다. 두 FRF의 정성적인 비교를 위하여 Fig. 10에 함께 나타내었으며 Fig. 10(a)에 작은 박스로 표시한 부분을 Fig. 10(b)에 확대하여 나타낸 결과, 최적 데이터 세트의 경우에 인접 주파수 간에 진폭 변화가 상대적으로 적게 나타나 랜덤오차가 매우 적음을 알 수 있다.
상기의 결과들은 임팩트 해머 실험을 통한 최적 FRF를 구함에 있어서 MS 유사성 함수가 매우 효과적으로 사용될 수 있음을 보여주고 있다.
4. 결 론
이 논문에서는 임팩트 해머 실험을 통하여 FRF를 구하고자 할 때, 가진 각도와 가진 위치 그리고 충격력과 충격시간 등 가진 환경을 동일하게 유지하기 힘든 실험적 제약 조건을 극복하고 채택/폐기 알고리즘이 없는 저가의 실험 장비를 이용해서도 MS 유사성 함수를 적절히 적용함으로써 양질의 FRF를 구하는 방법을 제안하였다.
MS 유사성 함수는 크기 유사성 함수와 모양 유사성 함수로 구분하여 나타내는데, 이 논문에서 다루는 응용(application)의 경우에는 크기 유사성 함수가 적합하고 이를 바탕으로 최적의 입력-출력 데이터 세트를 선별할 수 있음을 보여주었으며, 이를 이용하여 구한 최적 FRF의 질이 매우 우수함을 기여도 함수와 비교하여 검증하였다.
Acknowledgments
이 논문은 안동대학교 기본연구지원사업에 의하여 연구되었음.
References
-
Burgess, J. C., 1975, On Digital Spectrum Analysis of Periodic Signals, The Journal of the Acoustical Society of America, Vol. 58, No. 3, pp. 556~567.
[https://doi.org/10.1121/1.380705]

- Park, Y., 1992, Improved Estimation of Frequency Response Function, Proceedings of the KSNVE Annual Spring Conference, pp. 67~73.
-
Dishan, H., 1995, Phase Error in Fast Fourier Transform Analysis, Mechanical Systems and Signal Processing, Vol. 9, No. 2, pp. 113~118.
[https://doi.org/10.1006/mssp.1995.0009]

-
Fladung, W. and Rost, R., 1997, Application and Correction of the Exponential Window for Frequency Response Functions, Mechanical Systems and Signal Processing, Vol. 11, No. 1, pp. 23~36.
[https://doi.org/10.1006/mssp.1996.0084]

- Ahn, S. J., Jeong, W. B. and Kim, S. Y., 2002, An Enhancement of Transfer Function Synthesis by Improving the Leakage Error of FRF, Proceedings of the KSNVE Annual Autumn Conference, pp. 517~522.
-
Ahn, S. J. and Jeong, W. B., 2002, The Errors and Reducing Method in 1-dof Frequency Response Function from Impact Hammer Testing, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 12, No. 9, pp. 702~708.
[https://doi.org/10.5050/KSNVN.2002.12.9.702]

-
Ahn, S. J. and Jeong, W. B., 2003, FRF Distortion Caused by Exponential Window Function on Impact Hammer Testing and Its Solution, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 13, No. 5, pp. 334~340.
[https://doi.org/10.5050/KSNVN.2003.13.5.334]

- Lee, S., Yoon H. G. and Lee, J. W., 2014, Error Factors in Impact Hammer Test for Frequency Response Function, Proceedings of the KSME 2014 Fall Annual Meeting, pp. 1101~1103.
-
Lee, S. and Lee, J. W., 2016, Investigation of Error Factors from an Impact Hammer Test for Developing a Statistic Based Technique for Model Updating, Transactions of the Korean Society of Mechanical Engineers A, Vol. 40, No. 2, pp. 185~198.
[https://doi.org/10.3795/KSME-A.2016.40.2.185]

- Trethewey, M. W. and Cafeo, J. A., 1992, Tutorial: Signal Processing Aspects of Structural Impact Testing, The International Journal of Analytical and Experimental Modal Analysis, Vol. 7, No. 2, pp. 129~149.
-
Avitabile, P., 2017, Modal Testing: A Practitioner’s Guide, Wiley, Hoboken, NJ.
[https://doi.org/10.1002/9781119222989]

-
Brandt, A. and Brincker, R., 2011, Impact Excitation Processing for Improved Frequency Response Quality, Structural Dynamics, Vol. 3, pp. 89~95.
[https://doi.org/10.1007/978-1-4419-9834-7_9]

-
Shin, K., 2016, An Alternative Approach to Measure Similarity between Two Deterministic Transient Signals, Journal of Sound and Vibration, Vol. 371, No. 2016, pp. 434~445.
[https://doi.org/10.1016/j.jsv.2016.02.037]

-
Shin, K., Yang, H., Lee, S. and Lee, Y., 2013, Group Delay based Location Template Matching Method for the Identification of the Impact Location on a Plate, Journal of Sound and Vibration, Vol. 332, No. 8, pp. 2111~2117.
[https://doi.org/10.1016/j.jsv.2012.12.007]

-
Shin, K., 2016, Analysis of the Effect of the Grid Spacing on the Application of the Location Template Matching Method Using a Cantilever Beam, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 5, pp. 609~615.
[https://doi.org/10.5050/KSNVE.2016.26.5.609]


Jonghan Kim received his B.S. degree in Mechanical and Automotive engineering from Andong National University in 2015. He is currently working toward the M.S. degree in the Department of Automotive Engineering in Andong National University. His research interests include vibration testing and signal processing applications for machinery health monitoring.

Kihong Shin graduated in Precision Mechanical Engineering from Hanyang University in 1989. He received his MSc degree from Cranfield University, UK in 1992. He then completed his Ph.D. study at the ISVR in University of Southampton, UK in 1996. He is currently a Professor in the Department of Mechanical & Automotive engineering in Andong National University. His main research interests include signal processing for sound and vibration applications, vibration isolation and vibration testing, and machinery condition monitoring.