Tachi-Miura Polyhedron 실린더 구조에서의 비선형 탄성파 전파 특성에 관한 연구

1. 서 론

최근 진동 및 충격 저감을 위한 방법으로 기계적 메타물질(mechanical metamaterials)에 대한 연구가 활발히 수행되고 있다. 메타물질은 자연에서 발견되지 않은 특성을 가지도록 공학적으로 설계된 물질로 광학, 진동 분야에 적용되고 있다^(1,2). 최근 3D 프린팅 기술을 필두로 한 제작공법 및 재료공학의 발전으로 다양한 메타물질이 개발되고 있으며 이를 이용해 진동 저감, 주파수 차폐, 파동 경로 유도에 활용되고 있다.

기존에 진동 및 충격 저감을 위해 사용되는 메타물질의 형태는 반복적으로 배열된 격자구조 형태로 불연속적인 물질 사이의 기계적 물성 차이를 이용한다. 하지만, 최근 종이접기 구조를 기계적 메타물질의 구성요소로 사용하고자 하는 연구가 활발히 진행되고 있다^(3~5). 종이접기 구조는 제작이 기존 격자 방식의 메타물질보다 용이하고 크기의 제약이 없다는 장점이 있다. 종이접기 구조는 그 패턴의 종류에 따라 음의 푸아송 비(Poisson’s ratio)⁽⁶⁾, 다중 안정성(multi-stability)^(7,8)를 가질 수 있다. 또한, 하나의 패턴에서 접힘부의 변형을 통해 구조적 강성 변화를 유발할 수도 있다⁽⁹⁾. 위와 같은 특성들을 이용하여 로봇공학, 건축 등의 영역에 활용되고 있다. 하지만, 지금까지 종이접기 구조에 관한 연구는 정적(static) 또는 준정적(quasi-static) 영역에서의 구조적 특성 분석이 주로 이루어졌다. 동역학적 관점에서 종이접기 구조의 folding/unfolding 거동에 관한 분석은 극히 적은 연구사례들이 존재한다.

이에 이 연구에서는 종이접기 구조 패턴에서의 동역학 해석을 통해 비선형 탄성파 전파 특성을 분석하고자 한다. TMP(Tachi-Miura polyhedron) 패턴을 선정하여 해당 패턴으로 이루어진 실린더 구조에서의 동역학적 분석을 위해 유한요소 해석 환경을 구축하였다. TMP 패턴은 두 개의 시트로 구성되어 체적을 갖는 구조로 음의 푸아송 비와 쌍안정성이라는 구조적 특성을 가지고 있다⁽⁶⁾. 또한, strain-softening 거동을 나타내는데 이러한 특성은 충격 및 진동 저감에 활용될 수 있다⁽⁶⁾. 접힘부와 시트의 기하학적 구성을 통해 재료에 상관없이 비선형 거동을 보이기 때문에 기계적 메타물질의 구성요소로 활용될 수 있다. 또한, 실린더 형태의 구조를 연결하여 블록 형태의 구조를 제작할 수 있기 때문에 대형 구조에도 활용될 수 있다⁽¹⁰⁾.

이 연구에서는 TMP 구조에서의 strain-softening 거동을 조사하고 이에 의한 비선형 탄성파 전파 특성 분석을 위해 유한요소 해석 환경을 구축하였다. 구축된 해석 환경을 바탕으로 진동 및 충격 저감을 위한 TMP 실린더 구조를 모델링하였고 해당 구조에서의 탄성파 전파 특성을 분석하였다.

2. TMP 패턴의 구조적 특성

2.1 기하학적 형상

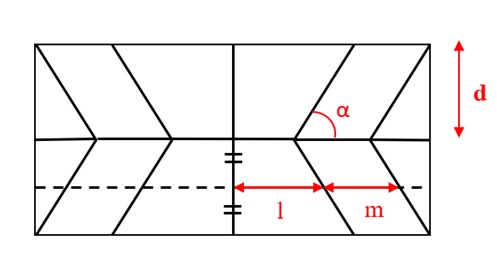
TMP 구조의 형상을 결정 짓는 기하학적 변수는 시트의 크기와 관련된 l, m, d와 각도 변수 α가 있다(Fig. 1). 해당 변수 값에 따라 구조의 형상 및 푸아송 비가 결정되지만 구조 강성과 같은 특성에는 큰 영향을 미치지 않는다⁽⁶⁾.

Fig. 1

Geometrical parameters for TMP unit cell

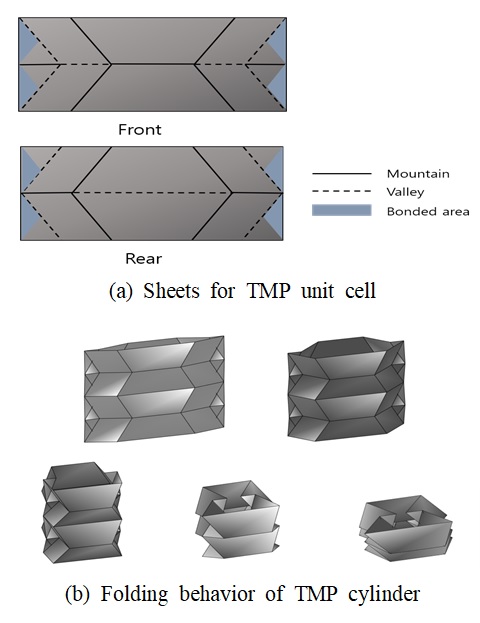
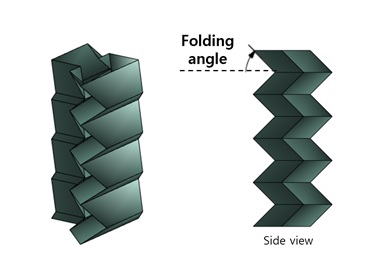
다양한 종이접기 패턴 중 TMP 패턴은 두 개의 시트로 구성되어 체적을 갖는 특징이 있다. Fig. 2와 같이 두 개의 시트가 결합하여 하나의 unit cell을 구성하게 되고 충분한 길이의 시트를 사용하면 TMP cylinder 구조를 제작할 수 있게 된다.

Fig. 2

Geometrical shape of TMP origami

2.2 Strain-softening Behavior

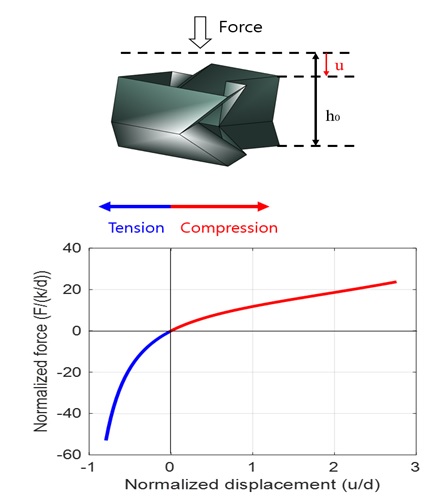
Yasuda 등⁽⁶⁾은 TMP 패턴의 접힘부를 torsional hinge로 모델링하여 동역학적 분석을 수행하였고 압축하중 하에서 strain-softening 거동이 나타남을 확인하였다. 힘-변위 관계식은 식 (1) ~ (4)를 통해 유도할 수 있고 Fig. 3과 같이 구조가 압축될수록 필요한 힘이 줄어들게 된다. 힘-변위 그래프에서 기울기는 구조적 강성을 의미하게 되고 압축 하중 하에서 구조 강성이 계속 줄어듦을 확인할 수 있다. 반대로 인장 하중 하에서는 구조 강성이 증가하게 된다.

$\[ \frac{F}{k/d}=-\frac{32}{\cos {\theta }_M}\left\{\begin{array}{l}\frac{2N-1}{2N}\left({\theta }_M-{\theta }_{M,0}\right)+\\ \left({\theta }_S-{\theta }_{S,0}\right)\frac{{\cos }^3{\theta }_G\sin {\theta }_M}{\cos \alpha \sin {\theta }_S}\end{array}\right\} \]$

(1)

$\[ {\theta }_M={\sin }^{-1}\left(\frac{h_0-u}{Nd}\right) \]$

(2)

$\[ {\theta }_G=2{\mathrm{t}\mathrm{a}\mathrm{n}}^{-1}\left(\tan \alpha \cos {\theta }_M\right) \]$

(3)

$\[ {\theta }_S={\mathrm{c}\mathrm{o}\mathrm{s}}^{-1}\left(\frac{\sin \left({\theta }_G/2\right)}{\sin \alpha }\right) \]$

(4)

N : Number of unit
θ₀ : Initial angle
k : Coefficient of torsional hinge

Fig. 3

Strain softening behavior described on force-displacement curve

해당 거동에 의해 구조상에서 탄성파 전파는 비선형적인 특성을 보이게 된다. 구조상에서 전파되는 탄성파의 속도는 구조 강성에 비례하게 되는데 압축 하중 하에서 구조 강성이 갈수록 작아지기 때문에 탄성파의 속도는 느려지게 되고 그 에너지는 점점 감쇠된다. 반대로 인장 거동에 의한 탄성파는 갈수록 빨라지기 때문에 그 에너지가 집중되는 현상이 나타나게 된다. 이러한 비선형적 특성에 의한 파동 왜곡(waveform distortion)에 의해⁽¹¹⁾ TMP 실린더 구조에 강력한 충격이 가해질 경우 먼저 발생한 압축 탄성파는 감쇠되고 후에 탄성력에 의해 발생하게 되는 인장 탄성파가 지배적으로 전파된다. 이러한 현상을 이용하여 충격 저감 구조 설계가 가능해지고 만약 실린더의 길이가 충분하다면 압축 하중이 가해졌음에도 구조의 끝부분에 인장 거동이 먼저 발생하는 특이한 현상이 발생하게 된다.

3. 유한요소 해석

3.1 모델링 기법

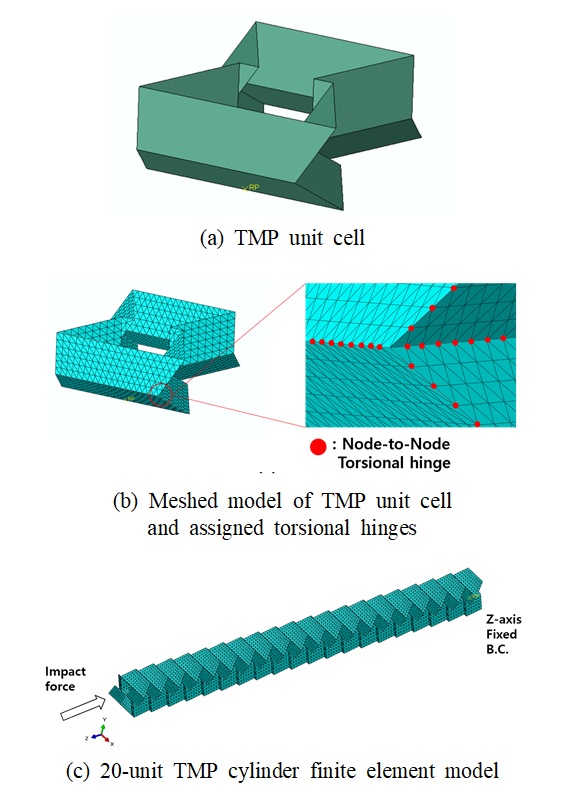
앞서 분석한 strain-softening 거동에 의한 비선형 탄성파 전파 특성을 분석하기 위해 유한요소 해석 기법을 사용하였다. 복잡한 형상의 종이접기 구조 모델링을 위해 파이썬 프로그래밍 언어 기반의 geometry 생성 코드를 작성하였고 이를 상용 구조해석 프로그램인 simulia ABAQUS에서 읽어 들여 하중 및 경계조건을 적용하였다. Fig. 4와 같이 모든 면을 유연 재료로 모델링하였고 충분한 요소로 meshing하였다. 요소 형태는 얇은 구조에 일반적으로 사용되는 3개의 node로 이루어진 삼각형의 shell(S3R)로 설정하였다. 종이접기 구조의 접힘부의 경우 node-to-node torsional hinge로 모델링하여 접힘부의 강성을 부여하였고 각 접힘부에 동일한 강성을 부여할 수 있도록 node 개수로 나누어 torsional hinge의 상수값을 부여하였다.

Fig. 4

Finite element model of TMP for analysis

TMP 실린더의 재질은 알루미늄으로 선정하여 재료적 물성치를 입력하였다(E=69 Gpa, ν=0.3, ρ=2.7 g/cm³). 기하학적 변수의 경우 다음과 같이 설정하였다(l, m, d, α)=(30 mm, 30 mm, 30 mm, 70°).

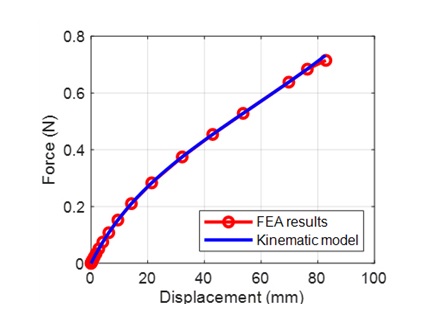
수립된 해석 환경을 기반으로 동역학적 분석을 하기에 앞서 유한요소 해석 기법의 정확성을 확인하기 위해 정적 해석(static analysis)을 수행하였다. 3개의 unit으로 이루어진 실린더 구조에 압축 하중을 가하여 force-displacement 데이터를 취득하였고 해당 결과를 Fig. 5와 같이 식 (1)과 비교하였다. 접힘부의 강성 값은 1 Nmm/rad, 초기 접힘각(Fig. 6)은 45°로 설정하였다. 정적 해석을 통해 TMP 실린더 구조 모델링 기법의 정확성을 일차적으로 확인하였다.

Fig. 5

Analytical results of FE model and comparison with kinematic model

Fig. 6

Definition of folding angle

3.2 초기 접힘각에 따른 탄성파 전파 특성

식 (1) ~ (4)에서 확인할 수 있는 것처럼 TMP 패턴의 strain-softening behavior에 영향을 주는 것은 초기 접힘각과 접힘부의 강성인 것을 알 수 있다. 식 (1)에 표현된 것처럼 접힘부의 강성(k)의 경우 구조 강성에 선형적으로 영향을 주게 되며, k 값이 커질수록 탄성파의 전파 속도가 빨라짐을 알 수 있다.

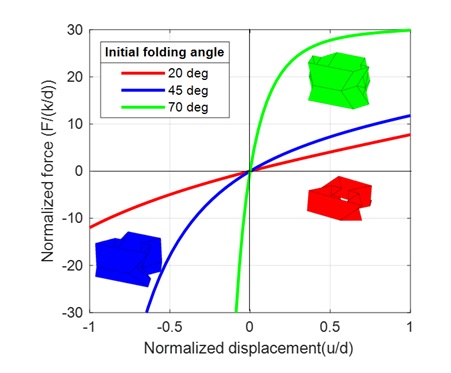
초기 접힘각에 따른 구조적 특성 변화는 Fig. 7을 통해 확인할 수 있다. 초기 접힘각이 클수록 구조 강성이 높아지게 되고 반대로 초기 접힘각이 작을수록 구조 강성이 낮아지게 된다. 이러한 특성에 의해 초기 접힘각의 크기와 탄성파의 전파 속도는 비례한다는 것을 알 수 있다. 이에 초기 각도가 20°, 45°, 70°인 TMP 실린더 구조를 각각 모델링하여 탄성파 전파 해석을 수행하였다. 모든 해석에 접힘부 강성은 1 Nmm/rad이다.

Fig. 7

Force-displacement curve corresponding to the initial folding angle

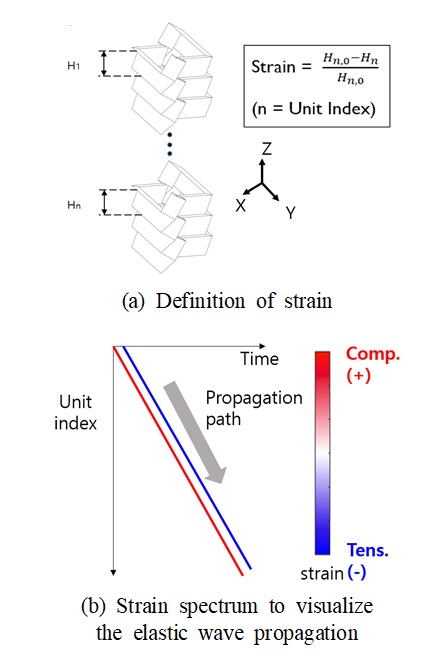
탄성파의 전파를 정량적으로 시각화여 특성을 분석하기 위해 unit cell의 strain을 정의하고 strain spectrum으로 표현하였다. TMP unit cell의 strain은 Fig. 8(a)와 같이 구조의 상대적 높이 변화량으로 정의하였고 압축 거동은 양의 부호(+)를, 인장 거동은 음의 부호(－)를 가지게 된다. 정의된 strain 값을 바탕으로 strain spectrum으로 표현함으로써 TMP 실린더에서의 탄성파 전파 특성 분석이 가능해진다. strain spectrum에서 x축, y축은 각각 시간, unit index를 나타내고 컬러맵은 strain 값으로 표현된다. 해당 spectrum을 통해 탄성파의 전파 속도를 비교할 수 있고 압축파, 인장파의 전파 특성을 시각적으로 확인할 수 있다.

Fig. 8

Definition of strain spectrum

3.3 해석 결과 및 의의

TMP 실린더의 마지막 유닛은 Z-axis fixed boundary condition을 적용하였고 충격 상황을 모사하기 위해 첫 유닛에 압축 방향으로 2 ms 동안 100 N의 힘을 가하였다. 해석 시간은 0.4초, time step은 0.0001 sec로 설정하여 충분한 시간 동안 계측하였다. 각 유닛 경계면의 변위 데이터를 저장하고 시간에 따른 각 unit의 strain 값을 계산하였다.

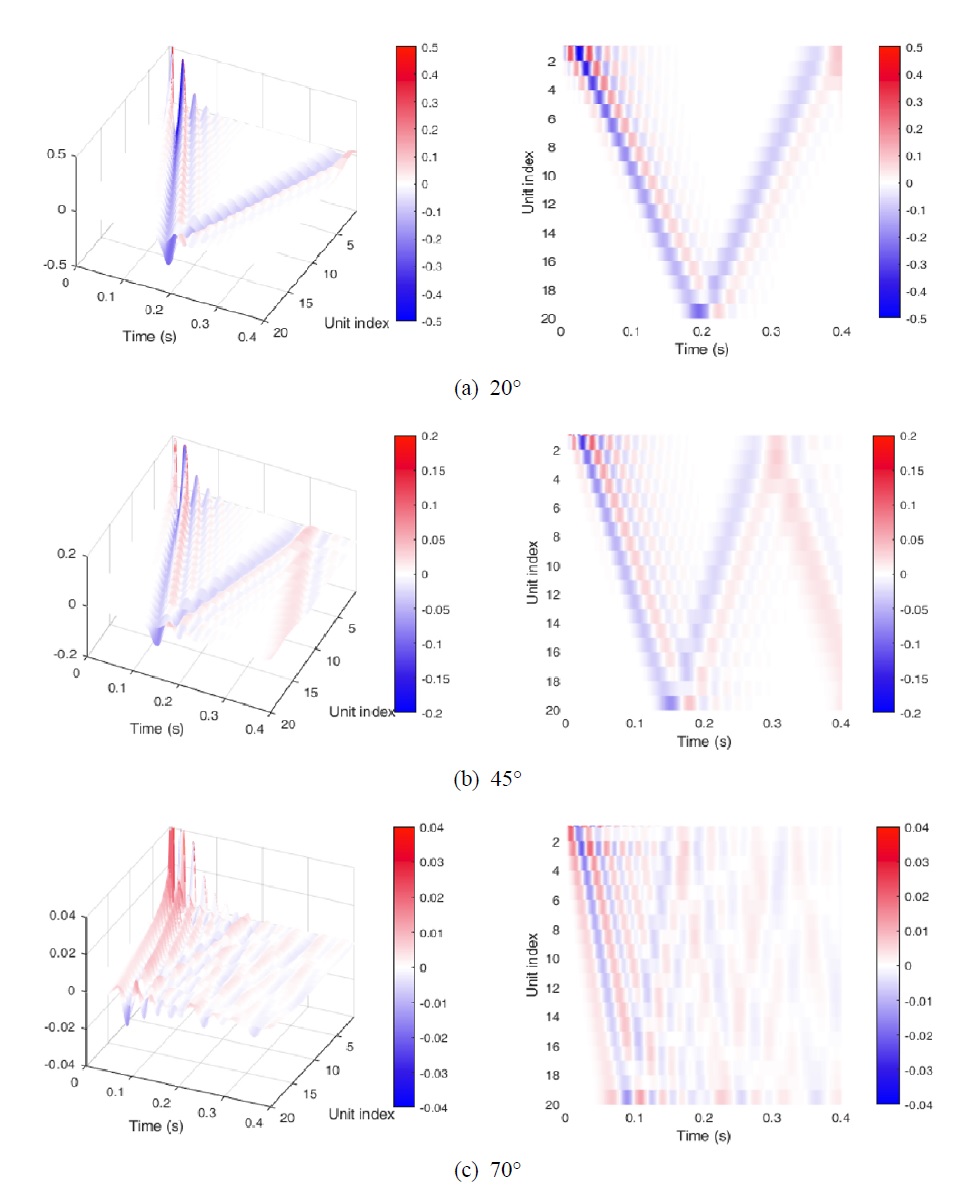
초기 접힘각에 따른 strain spectrum 결과들이 Fig. 9에 나타나 있다. 모든 경우에서 초기 충격이 가해진 상황을 살펴보면, 첫 unit에서 매우 큰 압축 파동이 발생함을 알 수 있다. 하지만, 해당 압축파는 빠르게 감쇠되어 strain 값이 작아지는 것을 알 수 있다. 또한, 구조의 탄성력에 의해 압축 거동 이후 인장 거동에 의한 탄성파가 생성되는 것을 확인할 수 있다. 초기 접힘각 20°, 45°의 경우 뒤늦게 생성된 인장파가 빠른 속도로 기존에 전파 중이던 압축파를 추월하여 마지막 unit에 먼저 도달하게 된다. 반면, 초기 접힘각이 70°인 해석 결과를 살펴보면, 두 파동이 거의 같은 속도로 전파되는 것을 확인할 수 있는데, 이는 Fig. 7에서 확인할 수 있는 것처럼 변위 구간에서 force-displacement curve가 거의 선형이기 때문이다. 반면, 다른 결과들은 변위 구간에서 strain-softening 거동이 두드러지기 때문에 두 파동의 속도 차이가 발생하게 된다. 이러한 결과와 마찬가지로 파동의 전파 속도를 비교해보면 구조 강성이 매우 큰 70° 경우가 가장 빠르고 구조 강성이 상대적으로 낮은 20° 경우에서 가장 느린 것을 확인할 수 있다.

Fig. 9

Numerical simulation results corresponding to the initial folding angle

이 해석 결과를 통해 TMP unit cell의 비선형적 특성이 탄성파 전파에 미치는 영향을 확인하였으며, 충격 저감에 있어서 효과적임을 확인하였다. 또한, 초기 접힘각에 따른 전파 특성을 비교 및 분석결과가 추후 TMP unit cell로 이루어진 충격 저감 구조 설계 시 활용될 수 있을 것으로 기대된다.

4. 결 론

이 연구에서는 Tachi-Miura polyhedron pattern으로 구성된 실린더 구조에서의 탄성파 전파 특성을 해석적으로 분석하기 위한 환경을 구축하였다. TMP unit cell의 strain-softening 거동에 비선형 파동 전파 특성을 분석하였고 초기 접힘각에 따른 특성 변화를 확인하였다. 해당 결과들은 종이접기 구조를 활용한 충격 저감 구조 설계에 활용될 수 있을 것으로 기대된다.

Acknowledgments

이 연구는 정부(과학기술정보통신부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(NRF-2021R1A2C2004563).

References

• Paulose, J., Meeussen, A. S. and Vitelli, V., 2015, Selective Buckling via States of Self-stress in Topological Metamaterials, Proceedings of the National Academy of Sciences, Vol. 112, No. 25, pp. 7639~7644. [https://doi.org/10.1073/pnas.1502939112]
• Coulas, C., Sounas, D. and Alù, A., 2017, Static Non-reciprocity in Mechanical Metamaterials, Nature, Vol. 542, pp. 461~464. [https://doi.org/10.1038/nature21044]
• Silverberg, J. L., Evans, A. A., McLeod, L., Hayward, R. C., Hull, T., Santangelo, C. D. and Cohen, I., 2014, Using Origami Design Principles to Fold Reprogrammable Mechanical Metamaterials, Science, Vol. 345, pp. 647~650. [https://doi.org/10.1126/science.1252876]
• Lv, C., Krishnaraju, D., Konjevod, G., Yu, H. and Jiang, H., 2014, Origami based Mechanical Metamaterials, Scientific Reports, Vol. 4, Article No. 5979. [https://doi.org/10.1038/srep05979]
• Waitukaitis, S., Menaut, R., Chen, B. G. and van Hecke, M., 2015, Origami Multistability: From Single Vertices to Metasheets, Physical Review Letters, Vol. 114, Article No. 055503. [https://doi.org/10.1103/PhysRevLett.114.055503]
• Yasuda, H. and Yang, J., 2015, Reentrant Origami-based Metamaterials with Negative Poisson’s Ratio and Bistability, Physical Review Letters, Vol. 114, Article No. 185502. [https://doi.org/10.1103/PhysRevLett.114.185502]
• Hanna, B. H., Lund, J. M., Lang, R. J., Magleby, S. P. and Howell, L. L., 2014, Waterbomb Base: A Symmetric Single-vertex Bistable Origami Mechanism, Smart Materials and Structures, Vol. 23, No. 9, Article No. 094009. [https://doi.org/10.1088/0964-1726/23/9/094009]
• Jianguo, C., Xiaowei, D., Ya, Z., Jian, F. and Yongming, T., 2015, Bistable Behavior of the Cylindrical Origami Structure with Kresling Pattern, Journal of Mechanical Design, Vol. 137, No. 6, Article No. 061406. [https://doi.org/10.1115/1.4030158]
• Suh, J. E., Kim, T. H. and Han, J. H., 2021, New Approach to Folding a Thin-walled Yoshimura Patterned Cylinder, Journal of Spacecraft and Rockets, Vol. 58, No. 2, pp. 516~530. [https://doi.org/10.2514/1.A34784]
• Yasuda, H., Gopalarethinam, B., Kunimine, T., Tachi, T. and Yang, J., 2019, Origami-based Cellular Structures with in Situ Transition between Collapsible and Load-bearing Configurations, Advanced Engineering Materials, Vol. 21, No. 12, Article No. 1900562. [https://doi.org/10.1002/adem.201900562]
• Hamilton, M. F., Blackstock, D. T. and Ostrovsky, L. A., 2008, Nonlinear Acoustics, Acoustical Society of America, Melville, NY.