전처리 되지 않은 진동 신호로 플랭크 웨어 예측하는 1D-CNN, 2D-CNN과 LSTM로 구성된 인공지능 네트워크
© The Korean Society for Noise and Vibration Engineering
Abstract
Turning processing machines have been widely employed due to their precision and versatility. As the number of cycles increases, the performance of these devices generally degrades owing to tool wear. Therefore, real-time tool condition monitoring (TCM) that utilizes statistical or machine learning methods has gained significant attention in both academia and industry. However, these methods necessitate sufficient data pre-processing, requiring a high degree of academic understanding as well as significant amount of time. Therefore, this research proposes an advanced artificial intelligence network to monitor a wide range of tools by utilizing raw signals without pre-processing. This study first developed a method consisting of 1D and 2D multi filters convolution neural networks (CNNs) and stacked long short term memories (LSTM). To activate the LSTM in a stable manner, the CNN plays a crucial role in dimensionality reduction. Accordingly, two dimensionality reduction approaches were proposed. These were layer normalized 1D&2D-CNN Multi filters. Then, following multi filters, the stacked LSTM was used to extract the sequential features. Next, the performance of the proposed network using the NASA milling dataset was observed and compared between the 1D/2D-CNN without Flank wear information, pre-processing, and previous research network inclusion. Consequently, although the 1D-CNN method did not have them, it achieved a similar level of accuracy as the present method using past Flank wear input.
Keywords:
Tool Condition Monitoring, Convolutional Neural Network, Long Short Term Memories, Flank Wear, 1D-CNN, 2D-CNN키워드:
툴 상태 감시, 합성곱 신경망, 장단기 메모리, 플랭크웨어, 1차원 CNN, 2차원 CNN1. 서 론
회전 기계 가공은 정밀한 가공과 기술의 유연성으로 제조 산업에서 많이 쓰이는 가공법이다. 일반적으로 기계 공정에서 직접적으로 워크 피스(work piece)를 연삭하는 툴은 사이클이 늘어남에 따라 비례해서 점진적으로 성능이 저하된다(1). 점진적인 성능 저하는 툴의 고장 및 생산물의 불량으로 이어진다. 툴의 고장은 생산품의 성능 저하나 기계 고장 같은 경제적 피해를 남긴다(2). 이런 측면에서 tool condition monitoring (TCM)은 결함을 사전에 예측하고 피해를 방지하는 중요한 역할을 한다. TCM을 평가하는 지표는 깨짐, 파손 그리고 측면 마모가 있다. 이 중 깨짐과 파손은 안정적 운행 상태에서 갑자기 나타나는 지표로 피해를 사전에 방지하기 어렵지만, 측면 마모는 서서히 발생하는 지표로 안정적 모니터링이 가능하다(3).
이러한 TCM 모니터링 방법으로는 기존에는 통계학을 기반으로 한 기법들이 사용했었다. Mohamed 등(4)은 3축 가속도계, 3축 동력계 신호의 root mean square (RMS), 평균, 분산, 첨도, spectral mean, spectral kurtosis, wavelet energy와 energy ratio의 특징을 데이터 전처리를 통해 추출했고, 이들 중 툴 마모와 피어슨 상관 계수(Pierson correlation coefficient)가 가장 높게 측정된 wavelet energy의 비율인 energy ratio를 선택해서 파티클 필터(particle filter)의 입력 데이터로 사용해 TCM을 평가했다. Karandikar 등(5)은 동력계 신호의 전처리를 통해 특징을 추출하고, 그 중 결정계수가 높은 두 개의 특징을 선택해서 naïve bayesian의 입력 데이터로 사용해서 TCM을 평가하는 기법을 제안했다. 통계적인 기법은 이처럼 신호들을 사용할 때 데이터 전처리가 필요하고, 툴 마모와 상관 계수나 결정 계수를 통해서 선택해야 한다. 이런 일반화 되지 않은 특징 추출 및 선택 방식은 연구자에게 높은 통계학적 지식과 많은 시간을 요구한다는 단점이 있다.
통계적 기법 외에도 머신 러닝(machine learning)을 활용하여 TCM을 평가하는 연구도 진행되고 있다. Zhou 등(6)은 토크 신호의 huang-hilbert transform (HHT)으로 다양한 시간-주파수 영역 스펙트럼으로 변환 뒤, long short term memories(LSTM)으로 신호를 진단 후 TCM을 평가하는 기법을 제안했다. Kim 등(7)은 continuous wavelet transform(CWT)을 이용해 소음 신호를 전처리했고, 시간-주파수 영역의 스펙트럼으로 변환 후 convolution neural network(CNN)으로 패턴을 분류해 TCM을 평가하는 방법을 제안했다. 또, Liang Guo 등(8)은 두 개의 회전 기계에 대한 TCM을 평가하기 위해 시간, 주파수 및 시간-주파수 영역에서 14개의 전처리 기법을 제시했다. 추가적으로 각각의 특징과 시간의 경과에 따른 선형적 유사성 및 특징의 단조로움(monotonicity)을 평가하는 수식을 통해 제안하여 선별했고, LSTM으로 이를 진단했다. 이와 같이 머신 러닝을 활용한 TCM의 경우도 분석하는 모델이나 시스템에 따라 전처리 기법들이 다양하기 때문에 일반화된 기법을 확립하기 어렵다는 한계점이 있다.
이를 극복하기 위한 기법으로는 입력 데이터로 raw signal을 이용하는 딥 러닝(deep learning) 기법이 있다. Zhao 등(9)은 동력계와 가속도계 raw signal을 LSTM으로 진단하는 방법을 제시하였다. 또, Cai 등(10)은 밀링 머신 운행 시 습득한 전류, 가속도 및 음향 신호(acoustic emission signal)를 전처리하지 않고 LSTM으로 신호를 진단해 TCM을 평가하는 방법을 제시하였다. 하지만 노이즈를 포함한 방대한 정보를 이용해서 진단하기에는 정확도가 떨어지거나(9), 이전 사이클의 플랭크 웨어(flank wear)를 입력 데이터로 사용해서(10) 정확도를 올려야 된다는 단점이 있다. 이전 사이클의 플랭크 웨어를 넣기 위해서는 매 싸이클마다 표면 특성을 측정해야 해서 시간소요가 크고 공정자동화에 단점이 있다. 즉, 딥러닝 훈련(training)을 위해서는 많은 데이터가 필요한데, 이를 위해서 매번 플랭크 웨어를 측정하는 것은 TCM 방법의 성능 향상에는 도움이 될지 모르나 효율성 및 실시간 모니터링 등에는 큰 악영향을 준다.
이 논문에서는 이전 플랭크 웨어와 전처리를 이용하지 않고, LSTM을 기반으로 하는 정확도 높은 네트워크를 제안하고자 한다. 해당 네트워크는 실시간 TCM이 가능하고 이전 플랭크 웨어를 입력으로 넣은 기존 방법과 유사한 정확도를 가진 효율적인 네트워크를 제안하고자 한다. 기존 방법(9,10)의 한계를 극복하기 위해 커널(kernel)이 다른 1D-CNN과 2D-CNN 네트워크를 LSTM 네트워크와 연결하는 방법을 제시하고자 한다. 이 방법론의 검증을 위해서 NASA 밀링 데이터(11)를 사용하여 그 특성을 검증하고 전처리를 사용하지 않은 기존의 연구(10)와도 비교하고자 한다.
2. 이 론
2.1 LSTM Network
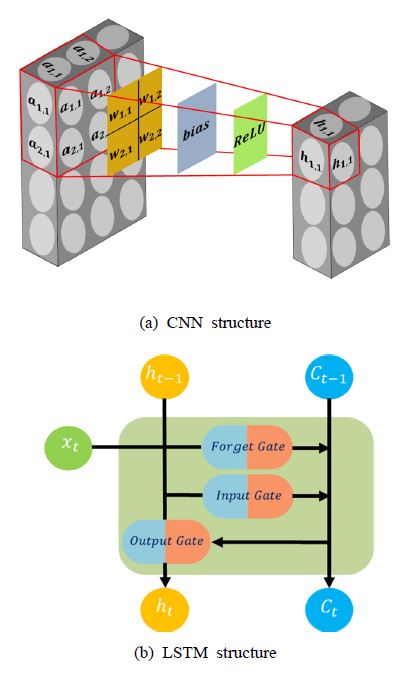
Raw signal을 분석하기 위한 딥 러닝 기법으로 LSTM을 채택하였다. 시계열적 특징을 추출하는 것에 우수한 LSTM은 메모리 셀(memory cell) 안의 세 개의 gate를 이용해 시계열적 특징을 추출한다. Gate들은 수학적인 관계를 통해 셀 스테이트(cell state) 값을 갱신하고, 이를 이용해 신호의 시계열적인 특성을 파악한다. Forget gate는 식 (1)과 같이 나타낼 수 있다.
| (1) |
시간 인덱스(index) t에서의 데이터 xt와 t-1에서 온 데이터 ht-1에 각각 가중치 를 곱하고 편향(bias)을 더해서 sigmoid 함수의 입력으로 사용해서 0 ~ 1의 값을 배출한다. 비슷한 구조가 input gate에서도 있는데, sigmoid 함수 외에 tanh 함수가 더해진 형태로 tanh 함수는 –1 ~ 1의 값을 배출한다.
| (2) |
| (3) |
| (4) |
식 (1) ~ (3)의 값을 hadarmard product를 적용한 식 (4)에 대입하여서 t-1 인덱스에서 온 Ct-1를 Ct와 같이 갱신한다.
| (5) |
| (6) |
마지막으로 갱신한 셀 스테이트 Ct와 output gate를 이용해 ht를 식 (5), 식 (6)과 같이 정의하고 t+1 인덱스에서 동일한 프로세스를 진행한다. 위와 같은 수학적 관계를 통해 순정파(feed forward propagation)가 이루어지고, 오차를 계산하고 역전파(back propagation)를 통해 오차를 최소화하는 가중치와 편향을 탐색하는 식으로 학습이 이루어진다. 이때, 이전의 데이터(ht-1)를 사용하여 단방향으로 순정파가 이루어지면 uni-LSTM이고 이전 데이터(ht-1)로 한 번 이후 데이터(ht+1)로 두 번 양방향으로 순정파가 이루어지면 Bi-LSTM이라 한다.
2.2 CNN
서론에서 설명했던 것처럼 raw signal을 단순히 LSTM 네트워크의 입력으로 사용하게 되면 성능이 떨어지게 된다. 이 논문은 데이터의 차원을 감소 (dimensionality reduction)시키고자 CNN을 채택하였다. Fig. 1에서 보이는 것처럼 CNN은 레이어가 거듭될수록 데이터의 크기를 감소시키는 것이 가능하다. CNN의 방식으로는 1D-CNN과 2D-CNN을 사용했고, 수학적 관계는 식 (7), 식 (8)과 같다.
| (7) |
| (8) |
h는 다음 레이어의 값, a는 이전 레이어의 값, t는 시간 인덱스, h는 높이, w는 폭을 의미한다. CNN은 식 (7), 식 (8)과 같은 수학적 관계로 순정파가 이루어지고 실제 값과의 오차를 계산하여 오차를 최소화하는 가중치와 편향을 탐색하는 역전파가 이루어지고 학습이 이루어진다.
3. 네트워크
3.1 정규화 멀티 필터 CNN
1D-CNN 필터는 3개의 1D-convolution layer로 이루어진 네트워크이다. 각각의 커널은 길이를 달리해 다양한 커널을 사용함으로써 데이터를 여러 측면에서 압축해서 다양한 특징을 추출할 수 있게 만든다.
2D-CNN 필터도 3개의 2D-convolution layer로 만든 네트워크이다. 2D 필터의 경우는 1차원 시계열 데이터를 2차원 데이터로 만들어줘야 한다. 이 논문에서는 행을 current축, 열을 segment축로 설정해서 1차원 데이터를 2차원 데이터로 변환한다. 예를 들어 1000개의 1차원 데이터를 (current, segment) = (50, 20) 조건으로 데이터를 나누면 1000×1의 행렬은 50×20의 2차원 데이터가 된다.
1D기반과 2D기반을 빠져나온 데이터는 channel squeezing를 통과하게 된다. 이 네트워크는 두 개 이상의 센서를 입력으로 쓸 때 1 커널 혹은 1×1 커널을 이용해 데이터 크기를 보존하면서 채널을 압축시키는 레이어이다. 2D기반의 경우 channel squeezing 후 2차원 데이터를 다시 1차원으로 flatten하는 과정을 추가적으로 거친다.
3.2 적층 LSTM 네트워크
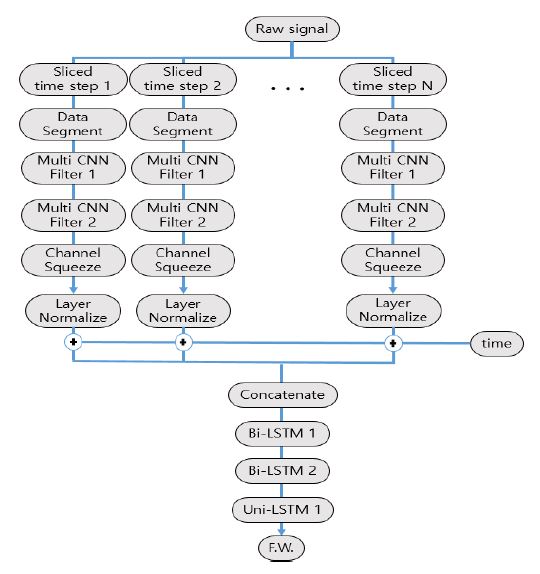
데이터 사이즈가 작아지고 정규화된 정규화 멀티 필터 CNN을 빠져나온 데이터들은 적층 LSTM 네트워크를 통과하여 시계열적 특성이 진단된다. 적층 LSTM 네트워크는 두 개의 bi-LSTM과 한 개의 uni-LSTM으로 이루어진 네트워크이다. 각각의 LSTM층은 dropout을 거쳐 그레디언트 익스플로딩 혹은 배니싱을 방지한다. 마지막으로, uni-LSTM을 통과한 데이터는 fully connected layer(FCL)의 입력 데이터로 사용되어 플랭크 웨어를 예측하게 된다. 3장을 종합한 전체 네트워크의 구조는 Fig. 2처럼 나타낼 수 있다.
4. 시뮬레이션
4.1 NASA 밀링 데이터셋
NASA에서 제공하는 데이터셋으로 밀링 머신을 다양한 조건에서 운행한 진동신호들의 정보를 담고있다(11). 진동신호들은 밀링 기계의 테이블의 AE센서, 가속도 센서와 밀링 기계 회전축의 AE 센서, 가속도 센서 그리고 모터 전류가 있다. 샘플링 주파수는 250 Hz이다. 케이스는 총 16개인데 Table 1처럼 컨디션 파라미터에 의해서 케이스가 나뉘어진다. 전체 데이터셋 중 테스트 데이터는 케이스 11, 12, 15와 16을 선정했고 나머지는 훈련데이터로 사용되었다.
한 사이클 당 각각의 센서는 9000번의 측정값이 있다. 이 중 플랭크 웨어가 측정되지 않았거나 사이클이 하나 밖에 없거나 데이터 길이가 다른 케이스는 사용하지 않았다.
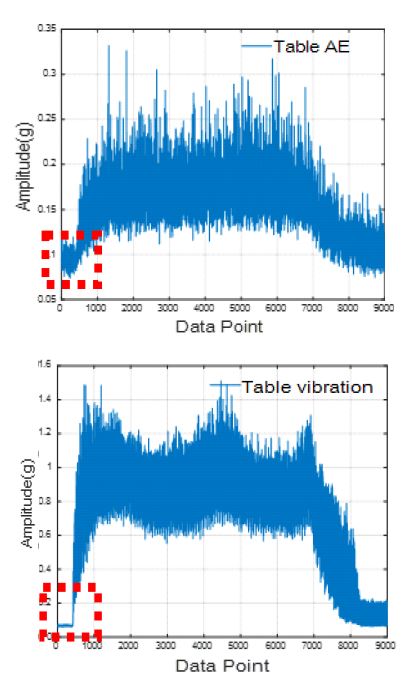
입력으로써 2개의 가속도계와 2개의 AE신호를 선택했다. 예를 들어 250 Hz의 낮은 샘플링 주파수에서 전류 신호가 유의미한 정보를 갖고 있지 않을 것으로 판단했다. 또, 9000개의 데이터를 1000개씩 9개로 나눠서 전체를 9개의 타임 스텝이 있는 데이터로 만들었다. 이때, 9개의 타임 시퀀스 중 처음의 1개 타임 스텝은 사용하지 않았는데 Fig. 3에서 보이는 것처럼 진폭이 낮다가 갑자기 높아진다. 이런 진폭이 낮은 부분은 툴이 워크피스를 가공하는 부분이 아닌 것으로 보인다. 이를 불필요한 정보이고 인공지능의 학습에 방해가 될 것이다. 또한 시간에 대한 경과를 반영하기 위해 컨디션 파라미터로 시간을 정규화하지 않고 입력으로 사용했다. 시간은 각 케이스마다 실험을 시작하고 끝날 때까지의 시간을 기록한 컨디션 파라미터다.
제안하는 딥 러닝 기법은 진동 신호에 대한 진단을 인공신경망을 통해서만 이루어진다. 그렇기 때문에 하이퍼 파라미터(hyper parameter)의 선택에 있어 신중할 필요가 있다. 이 연구에서 1D-CNN 기반 시뮬레이션을 위한 네트워크의 최적화된 하이퍼 파라미터는 실험적으로 찾아냈고, 결과로 Table 2, Table 3과 같이 설정했다. 커널의 길이가 다른 3개의 CNN필터의 이름을 kernel long, kernel mid 그리고 kernel short로 지었고, 각각 150, 100, 50으로 설정했다.
4.2 시뮬레이션 결과
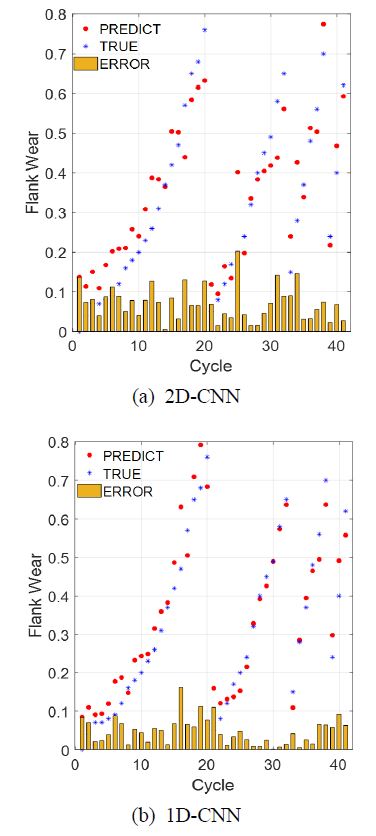
Fig. 4는 전체 테스트 데이터에 대한 실제값(붉은 점)과 진동 데이터를 이용한 인공지능의 예측값(푸른 점)을 나타내고 있다. Fig. 4에 보는 것과 같이 이전의 플랑크 웨어를 사용하지 않고도 경향성을 잘 따라가는 것을 볼 수 있다. 1D 기반 네트워크의 경우 모든 테스트 케이스 RMSE는 0.0581이 나왔으며, 테스트 케이스 평균 RMSE는 0.0555가 나왔다. 2D 기반 네트워크의 경우 모든 테스트 케이스 RMSE는 0.0812이 나왔으며, 테스트 케이스 평균 RMSE는 0.080725가 나왔다.
Table 4는 선행연구에서 제시한 앞선 플랭크 웨어를 넣은 경우와 그렇지 않은 경우 또 본 연구에서 제시한 1D와 2D-CNN기반의 네트워크에 대한 결과를 보여준다. 앞선 플랭크 웨어를 넣은 경우가 평균 0.045 RMSE를 보였다면, 앞선 플랭크 웨어의 입력이 없는 경우는 0.2868로 큰 오차를 보였다. 그러나 1D-CNN기반의 결과는 0.0581 RMSE의 값으로 앞선 플랭크 웨어를 사용하지 않는 경우 대비 약 390 %의 성능향상이 있었고, 플랭크 웨어를 사용한 경우와 유사한 정도의 성능을 보였다.
5. 결 론
이 논문에서는 현대 산업에서 중요하게 사용되는 회전 기계 가공의 TCM을 복잡한 전처리 과정과 이전 싸이클의 플렝크 웨어의 측정 없이 1D-/2D-CNN과 적층 LSTM 딥 러닝 기법을 이용하여 수행할 수 있음을 확인하였다. 제한한 1D-CNN방법은 NASA 밀링 데이터셋을 이용한 시뮬레이션에서 이전 플랭크 웨어를 사용하고 전처리 방법을 사용한 경우의 값인 RMSE 0.045와 이전 플랭크 웨어와 전처리를 사용하지 않았음에도 불구하고 유사한 0.058의 성능을 보여줌을 확인하였다. 또한, 더욱 복잡한 2D-CNN 모델보다 1D-CNN 방법이 더욱 뛰어난 결과를 보여줌을 확인하였다. 즉, 기존과 같이 복잡한 방법이 아닌 1D-CNN기반의 적층 LSTM 네트워크를 구축하고 최적화된 하이퍼 파라미터값을 적용하면 월등한 효율성과 정확성의 TCM 예측 모델을 구축할 수 있음을 확인하였다.
Acknowledgments
이 연구는 방위사업청과 방위산업기술지원센터의 지원(사업명: 선체 부착 센서를 이용한 함정추진기 CIS 모니터링 기술, 계약번호: UC200001D)하에, LIG넥스원 위탁연구(계약번호: LIGNEX1-2021-0794(00))로 진행되었습니다.
References
- Lee, Y. K., Choi, S. K., Yoon, K. C. and Lee, Y. S., 2003, NRRO Analysis of 3.5inch HDD Spindle Ball Bearings utilizing the Measured Geometric Imperfection, Proceedings of the KSNVE Annual Spring Conference, pp. 585~591.
-
Kim, N. H., Choi, J. H. and An, D., 2017, Prognostics and Health Management of Engineering Systems: An Introduction, Springer, Cham.
[https://doi.org/10.1007/978-3-319-44742-1_1]

-
Mohamed, A., Hassan, M., M`Saoubi, R. and Attia, H., 2022, Tool Condition Monitoring for High-performance Machining Systems – A Review, Sensors, Vol. 22, No. 6, Article No. 2206.
[https://doi.org/10.3390/s22062206]

-
Wang, J., Wang, P. and Gao, R. X., 2015, Enhanced Particle Filter for Tool Wear Prediction, Journal of Manufacturing Systems, Vol. 36, pp. 35~45.
[https://doi.org/10.1016/j.jmsy.2015.03.005]

-
Karandikar, J., McLeay, T., Turner, S. and Schmitz, T., 2015, Tool Wear Monitoring using Naïve Bayes Classifiers, International Journal of Advanced Manufacturing Technology, Vol. 77, No. 9, pp. 1613~1626.
[https://doi.org/10.1007/s00170-014-6560-6]

-
Zhou, J. T., Zhao, X. and Gao, J., 2019, Tool Remaining Useful Life under Variable Working Conditions, International Journal of Advanced Manufacturing Technology, Vol. 104, pp. 4715~4726.
[https://doi.org/10.1007/s00170-019-04349-y]

-
Kim, S., An, K., Baek, J., Lee, S., Lee, C. and Kim, P., 2021, Health Monitoring of Power Driving System using Sound Signal based on Deep Learning, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 1, pp. 47~56.
[https://doi.org/10.5050/KSNVE.2021.31.1.047]

-
Guo, L., Li, N., Jia, F., Lei, Y. and Lin, J., 2017, A Recurrent Neural Network based Health Indicator for Remaining Useful Life Prediction of Bearings, Neurocomputing, Vol. 240, pp. 98~109.
[https://doi.org/10.1016/j.neucom.2017.02.045]

-
Zhao, R., Wang, J., Yan, R. and Mao, K., 2016, Machine Health Monitoring with LSTM Networks, Proceedings of 2016 10th International Conference on Sensing Technology (ICST).
[https://doi.org/10.1109/ICSensT.2016.7796266]

-
Cai, W., Zhang, W., Hu, X. and Liu, Y., 2020, A Hybrid Information Model based on Long Short‑term Memory Network for Tool Condition Monitoring, Journal of Intelligent Manufacturing, Vol. 31, pp. 1497~1510.
[https://doi.org/10.1007/s10845-019-01526-4]

- Goebel, K., 1996, NASA Mill Data Set, NASA.
- Ioffe, S. and Szegedy, C., 2015, Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift, Proceedings of Machine Learning Research, Vol. 37, pp. 448~456.
-
Laurent, C., Pereyra, G., Brakel, P., Zhang, Y. and Bengio, Y., 2016, Batch Normalized Recurrent Neural Networks, Proceedings of 2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), pp. 2657~2661.
[https://doi.org/10.1109/ICASSP.2016.7472159]

- Ba, J. L., Kiros, J. R. and Hinton, G. E., 2016, Layer Normalization, arXiv Preprint, arXiv: 1607.06450.

Jung-Woo Kim was born in Anyang, Korea, in 1995. He is currently an undergraduate student in the Gachon University. His research interest is artificial intelligence.

Kyoung-Su Park was born in Seoul, Korea, in 1976. He received the B.E. degree in electrical-mechanical engineering from the Yonsei university, Seoul, Korea, in 2000, and the master and Ph.D. degrees in mechanical engineering from the Yonsei University, Seoul, Korea in 2002 and 2006, respectively. In 2006, he joined the Samsung Electronics Corp. and he has worked for about three years. Since September 2008, he has been a research professor in the school of mechanical engineering at the Yonsei university. And he has become an associate professor in mechanical engineering at Gachon university since 2014. His current research interests include the vibration and control issues and intelligent approaches for cable-driven parallel robot and for nano/micro environment. He has served as executive member for more than 13 years in ASME-ISPS (Information Storage and Processing System) and he became a chair of ASME-ISPS division from July 2016 to August 2017.