수치해석을 이용한 1-3 압전복합체 적용 판형 구조 수동센서의 음향특성 분석

1. 서 론

일반적으로 소나에 사용되는 수신용 센서는 배경소음에 대한 이득 및 지향성 확보를 위해 일정 크기의 음향길이/면적이 필요하며, 이를 위해 단위 음향 센서가 평면 또는 곡면으로 배열된 형태가 주로 사용된다. 배열 센서를 구성하는 단위 음향 센서는 일반적으로 PZT 계열의 압전 세라믹을 하이드로폰 소자로 많이 사용한다. 압전 세라믹은 전기-기계 결합계수가 높아 고효율의 음향 센서를 설계할 수 있지만 음향 임피던스가 높아 정합이 어렵다. 또한 수신용 소자의 주요 특성인 정수압 성능지수(hydrostatic figure of merits, FOM)가 낮은 것이 단점이다. 따라서 압전 세라믹 대비 FOM이 훨씬 높고 유전 손실과 음향 임피던스가 매우 낮은 압전복합체를 하이드로폰 소자로 활용하는 방안이 적합한 대안으로 떠오르고 있다.

복합재료에 대한 연구는 대표적으로 1-3, 2-2형 압전복합체가 있으며, 이 중 1-3형 압전복합체가 특성상 다양한 장점이 있어 많이 활용되고 있다^(1~4). 1-3형 압전복합체의 음향 센서 적용 관련 연구는 다수의 기존 사례들이 있다. Bowen은 압전복합체 판넬 제작 후 트랜스듀서에 적용하여 송수신 특성을 측정하였다⁽⁵⁾. Gibiansky는 음향 특성 최대화를 위한 압전복합체의 구조 최적화에 대한 연구를 수행하였다^(6,7). 그러나 이러한 선행 연구 사례들의 경우 압전복합체 구조에 대한 분석 및 설계에 중점이 맞춰져 있다.

배열 센서를 구성하는 단위 음향 센서는 음향 수신 특성을 향상시키기 위하여 일반적으로 하드 배플이 적용된 판형 구조를 갖는 경우가 일반적이다. 하지만 이러한 판형 구조 수동센서는 배플의 진동 모드로 인한 음향 센서의 수신 특성에 왜곡이 발생한다. 특히 1-3형 압전복합체를 하이드로폰 소자로 사용하는 경우 배플에 밀착되는 구조로 설계하기 때문에 배플의 진동 모드 영향을 크게 받는다. 따라서 1-3형 압전복합체가 적용된 판형 구조 수동센서는 배플의 진동 모드 영향을 최소화 할 수 있는 방안에 대한 연구가 필요하다.

이 연구에서는 수치해석을 이용하여 판형 구조 수동센서의 배플 진동 모드 특성과 수신 전압 감도(receiving voltage response, RVS) 변화를 분석하였다. 최종적으로는 판형 구조 수동센서의 높은 수신이득 효과를 얻을 수 있는 배플 제원과 배플의 진동 모드가 발생한 주파수에서의 RVS 레벨 변화를 최소화할 수 있는 방안을 도출하였다.

2. 1-3형 압전복합체 해석

1-3형 압전복합체 모델은 선행 연구 사례들을 참고하여 폴리머 모재 종류에 따른 FOM 특성 변화를 분석하고 높은 FOM과 RVS에 적합한 압전 세라믹 부피비와 폴리머 모재를 선택하였다. 압전 세라믹 삽입재로는 PZT-4를 사용하였으며, 해석에 적용한 폴리머 모재의 물성은 Table 1과 같다.

Table 1

Material properties of the components of the 1-3 piezoelectric composite

1-3형 압전복합체의 FOM은 다음과 같이 수식 (1) ~ (3)을 이용하여 계산할 수 있다^(8,9). 수식에서 d₃₁, d₃₃, d_h는 압전 변위 상수를, g_h는 정수압 압전 전압 상수를, K는 유전상수, ε₀는 진공의 유전율 값을 나타낸다.

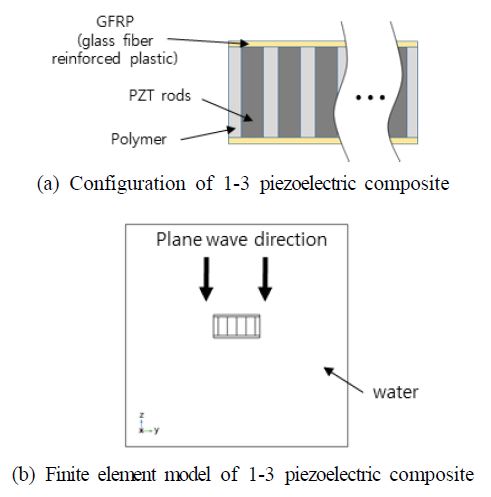
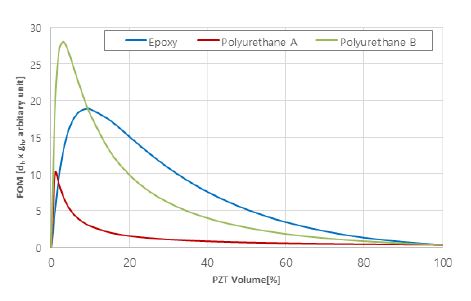
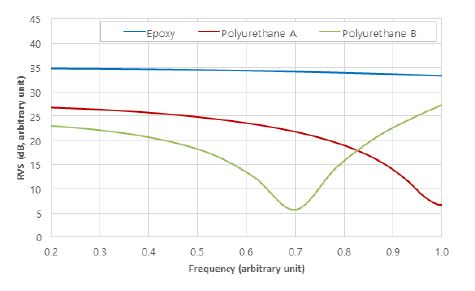
수치해석 및 FOM 계산을 위한 1-3형 압전복합체 모델은 Fig. 1(a)와 같다. GFRP는 정수압에서의 성능을 높이고 도금 처리된 전극을 보호하기 위함이다. RVS는 Fig. 1(b)와 같이 1-3형 압전복합체에 평면파를 입사시킨 다음 압전복합체에 발생 되는 출력 전압을 이용하여 계산하였다. 먼저, 폴리머 모재의 종류와 세라믹의 부피비에 따른 FOM 계산 결과는 Fig. 2와 같다. 해석에 적용한 1-3형 압전복합체는 세라믹의 부피비가 10 %이하인 조건에서 폴리머 모재가 polyurethane B로 구성되었을 때 FOM이 가장 크다. 그러나 세라믹의 부피비가 낮을수록 1-3형 압전복합체의 정전용량이 낮아지기 때문에 수신 회로 입력단의 전기적 잡음 특성에 큰 영향을 미친다. 따라서 전기적 잡음 특성을 고려하여 최소한의 정전용량을 확보할 필요가 있었고, 또한 제작성과 수율을 고려하여 세라믹의 부피비를 30 %로 제한하였다. 이러한 경우 epoxy가 1-3형 압전복합체 해석 모델의 폴리머 모재로 가장 좋은 것을 확인하였다. 다음으로 세라믹의 부피비를 30 %로 고정하고 폴리머 모재 종류에 따른 RVS를 유한요소법을 이용하여 비교한 결과는 Fig. 3과 같다. 앞서 보인 FOM 결과와 마찬가지로 세라믹의 부피비가 30 %인 1-3형 압전복합체 모델의 폴리머 모재를 epoxy로 사용하는 경우 RVS가 가장 높고, 관심 주파수 전 대역에서 평탄한 특성을 가지는 것을 확인할 수 있다. 따라서 이 논문에서 적용한 1-3형 압전복합체 모델은 폴리머 모재를 epoxy로 사용하여 판형 구조 수동센서 모델에 적용하였다.

Fig. 1

Simulation model of 1-3 piezoelectric composite

Fig. 2

FOM curves of volume ratio PZT in 1-3 composites with each polymer materials

Fig. 3

RVS curves of 1-3 composites with each polymer materials

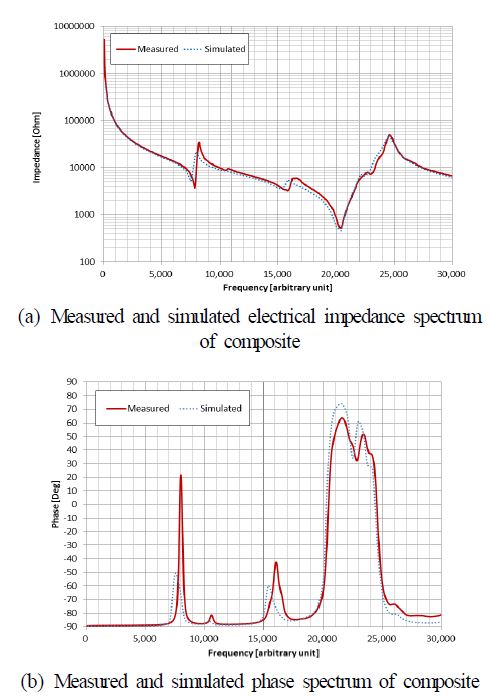
다음으로 유한요소 해석 결과의 타당성을 검증하기 위해 1-3형 압전복합체 시편을 제작하고, 특성을 측정하였다. 앞서 설계된 1-3형 압전복합체는 사출 금형 방법을 이용하여 제작하였으며, 제작된 1-3형 압전복합체는 Fig. 4와 같다. 1-3형 압전복합체의 공기 중 임피던스를 서로 비교하기 위해 유한요소 해석을 수행하였고, 제작된 1-3형 압전복합체 시편의 전기-기계 임피던스 크기 및 위상은 임피던스 분석기(4294A, agilent) 이용하여 전기-기계 임피던스를 측정하였다. 유한요소법으로 분석된 압전복합체의 임피던스와 제작된 시편으로 측정된 임피던스를 비교하여 그림 5에 나타내었다. Fig. 5(a)는 공기 중 전기-기계 임피던스의 크기, (b)는 공기 중 임피던스의 위상을 비교하여 나타낸 스펙트럼이다. 비교 결과, 전 주파수 영역에서 유한요소 해석 결과와 시편의 측정 결과가 공진주파수 기준 각각 20 417와 20 381이고 오차는 0.17 %로 거의 일치함을 확인할 수 있었다. 이를 통해 앞서 분석된 유한요소 해석 결과의 타당성을 검증할 수 있었다. 따라서 압전 복합체와 배플로 구성된 판형 수동센서의 RVS 특성도 유한요소법을 이용하여 분석하였다.

Fig. 4

Manufactured 1-3 piezoelectric composite pannel

Fig. 5

Measurement and simulation results of 1-3 piezoelectric composite

3. 판형 구조 수동센서 해석

3.1 수신감도 분석

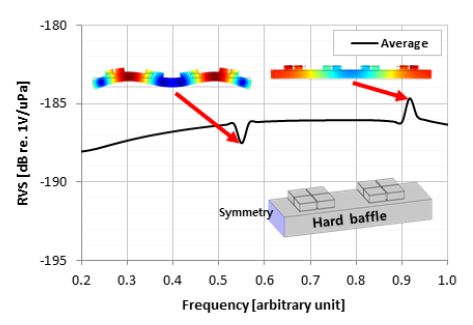
1-3형 압전복합체가 적용된 판형 구조 수동센서는 배플과 1-3형 압전복합체 간 간격을 최소화할 수 있기 때문에 수신이득 효과를 극대화할 수 있는 장점이 있다. 하지만 배플과 1-3형 압전복합체 간 간격이 가까울수록 배플에서 발생되는 진동 모드 영향을 크게 받기 때문에 음향 센서의 수신 특성에 왜곡이 발생한다. Fig. 6는 4×4 배열 구조(4채널 구성, 채널당 1-3형 압전폭합체 4개) 1-3형 압전복합체가 적용된 기존의 판형 구조 수동센서에 대한 RVS 곡선이다. 해석 결과에서 보이는 것과 같이 정규화 주파수 0.55와 0.9에서 배플의 진동 모드로 인해 RVS 변화가 발생하는 것을 확인할 수 있다. 따라서 이 논문에서는 Fig. 7과 같이 기존의 판형 구조 수동센서 모델을 간략화 하여 배플의 폭, 길이, 두께에 따른 1-3형 압전복합체의 수신 특성 변화를 분석하였다. 또한 1-3형 압전복합체 간 간격을 변경하여 배플의 진동 모드로 인해 발생하는 RVS 레벨 변화를 최소화할 수 있는지를 검토하였다. Fig. 7의 ×1은 배플의 폭, ×2는 배플 두께, ×3은 배플의 길이, ×4는 1-3형 압전복합체 간 간격이다. 유한요소 해석을 위한 툴로는 COMSOL multiphysics를 사용하였고, Fig. 7에 표현된 것과 같이 symmetry boundary condition 조건을 주어 전체형상의 절반만 모델링 하여 모델을 간략화하고 해석에 소요되는 리소스를 줄일 수 있었다.

Fig. 6

RVS curves of original model

Fig. 7

Configuration of simple model

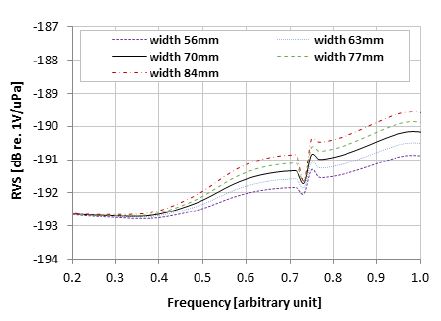
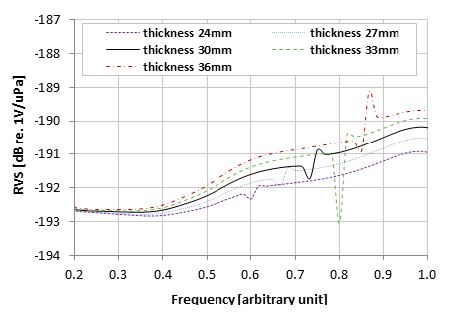
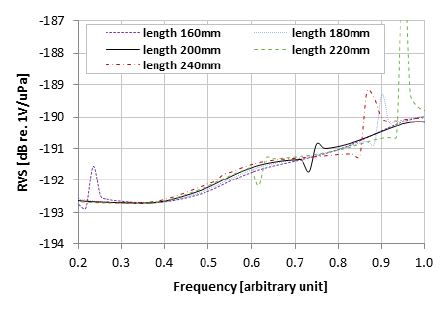
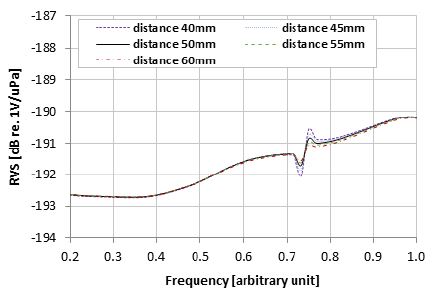
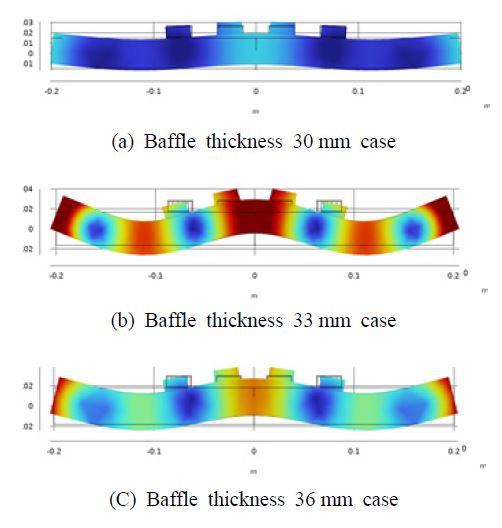
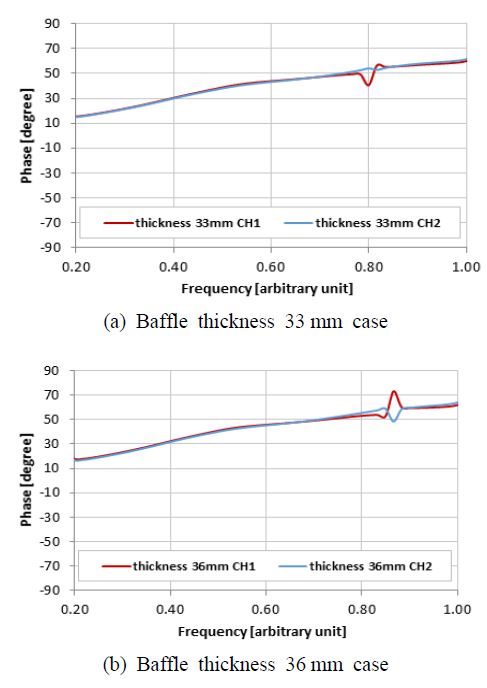
Figs. 8~11는 각각 Fig. 7 해석 모델의 ×1, ×2, ×3, ×4 변화에 따른 RVS 스펙트럼 해석 결과이다. 배플 적용으로 얻는 수신이득 효과의 경우 ×1, ×2의 영향이 큰 것을 Fig. 8과 Fig. 9을 통해 확인할 수 있다. 일반적으로 배플 두께가 음파 반사에 가장 큰 영향을 주지만 해석에 적용한 간략화 모델의 경우 배플 두께 ×2의 변화 수준이 3 mm로 매우 작기 때문에 이 논문에서 고려한 주파수 대역에서는 배플 폭 X1보다 영향이 적은 것으로 확인되었다. ×3과 ×4는 수신이득 효과에 영향이 없다. ×3의 경우 Fig. 10과 같이 배플 진동 주파수가 가장 크게 바뀌고 배플 길이 X3이 길어짐에 따라 배플 진동 주파수가 저주파수 대역으로 이동하는 것을 확인할 수 있다. ×4는 RVS 레벨 변화만 영향을 주는 것을 Fig. 11를 통해 확인할 수 있다. 한편 ×2의 경우 배플 진동 모드로 인한 RVS 레벨 변화가 30 mm에서 36 mm로 변하는 구간에서는 비선형적인 특성인 것을 Fig. 9을 통해 확인 가능하다. Fig. 12은 배플 두께 ×2의 진동 모드 형상을 동일한 위상에서 비교한 그림이다. RVS 레벨 변화와 마찬가지로 Fig. 12(b) ×2 33 mm 모델의 최대 변위가 Fig. 12(c) ×2 36 mm인 모델보다 더 크다. 따라서 배플의 진동 모드로 인한 변형이 클수록 RVS 레벨 변화가 크게 발생하는 것을 알 수 있다. 또한 Fig. 9의 비선형적인 특성을 보이는 구간은 변곡점의 발달 방향도 다르다. 배플 두께 ×2가 33 mm인 모델의 변곡점은 RVS 레벨 변화가 감소하는 방향이지만 ×2가 36 mm인 모델은 반대의 경우를 보인다. 이는 Fig. 13과 같이 각 모델의 복소모드 위상 차이로 인해 수중청음기의 전압 출력 위상이 다른 것으로 확인되었다. 그래프에서 CH1은 내부에 위치한 1-3형 압전 복합체를 의미하고, CH2는 외부에 위치한 1-3형 압전 복합체를 의미한다.

Fig. 8

RVS curves of baffle width(X1) variation

Fig. 9

RVS curves of baffle thickness(X2) variation

Fig. 10

RVS curves of baffle width(X3) variation

Fig. 11

RVS curves of distance between hydrophones(X4) variation

Fig. 12

Comparison of mode shape at resonance frequency

Fig. 13

Comparison of phase curves of voltage at baffle vibration mode frequency

3.2 해석 결과 비교

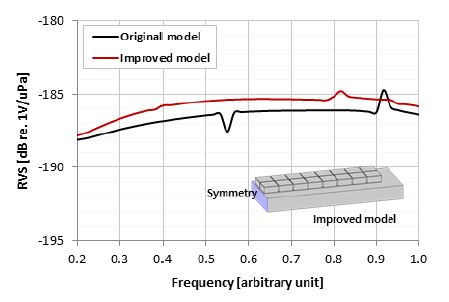
결론적으로 Fig. 7과 같은 모델의 판형 구조 수동센서는 1-3형 압전복합체를 적용하는 경우 배플의 폭과 두께 변화에 따른 선형적인 수신이득 효과를 얻을 수 있었다. 배플의 진동 모드로 인해 발생하는 특정 주파수에서의 널 크기 변화는 Fig. 11과 같이 1-3형 압전복합체 간 간격을 조절하여 줄일 수 있다. 이는 배플의 공진 점에서의 nodal line과 1-3형 압전복합체 위치에 따라서 구조 공진의 영향을 크게 또는 작게 받을 수 있기 때문인 것으로 보인다. 이 해석에서는 3차 공진의 형태만 나타나고 있으나 요구되는 주파수 대역에 따라서 다른 차수의 공진이 복합적으로 나타나기도 한다. 따라서 배플의 진동 모드 특성과 1-3형 압전복합체 위치 변경에 따른 널 크기 변화 내용을 바탕으로 얻은 결론은 다수의 1-3형 압전복합체 적용으로 평균효과를 기대한다면 배플 진동 모드 특성이 상쇄되어 RVS 평탄화 효과를 가질 수 있을 것으로 판단된다. 평균효과를 위해 배플 위에 최대한 대면적으로 배치 가능한 4×8 배열 구조를 적용하였다.

앞에서 분석한 내용을 바탕으로 판형 구조 수동센서를 개선한 모델과 기존 모델의 RVS 곡선을 비교한 결과는 Fig. 14와 같다. 개선된 모델은 기존의 판형 구조 수동센서 모델보다 배플 폭이 약 35% 증가했기 때문에 높은 수신이득 효과를 얻을 수 있었다. 또한 배플의 길이는 약 10 % 길게 늘리고 두께는 2 mm 얇게 적용했기 때문에 배플의 진동 모드 주파수는 저주파수 대역으로 이동한 것을 확인할 수 있다. 마지막으로 1-3형 압전복합체 4×4 배열 구조를 4×8 배열 구조로 2배 더 넓게 적용하여 평균효과를 기대한 결과 배플 진동 모드로 인한 RVS 변화를 최소화할 수 있음을 보여준다.

Fig. 14

Comparison of original model and optimized model RVS curves

4. 결 론

1-3형 압전복합체가 적용된 판형 구조 수동센서는 배플의 진동 모드로 인해 음향 수신 특성이 왜곡되는 현상을 고려해야 한다. 이 논문에서는 유한요소해석을 통해 배플의 폭, 길이, 두께와 1-3형 압전복합체 간 간격을 변경하여 판형 구조 수동센서의 수신 특성 변화를 분석하였다. 이를 통해 배플의 진동 모드로 인해 발생하는 RVS 레벨 변화를 최소화할 수 있는 방안에 대해 검토하였다. 해석 결과 기존의 판형 구조 수동센서 모델은 배플의 폭과 두께가 충분히 확보되어야 높은 수신이득 효과를 얻을 수 있다. RVS 레벨 변화는 1-3형 압전복합체 간 간격 변경으로 줄일 수 있는 것을 확인하였다. 결론적으로 평균효과를 높일 수 있도록 다수의 1-3형 압전복합체를 배열 구조로 적용하는 방법을 유추하였고 개선된 모델에 적용한 결과 배플의 진동 모드로 인해 발생하는 RVS 레벨 변화를 최소화할 수 있음을 확인하였다.

Acknowledgments

이 연구는 국방과학연구소의 지원을 받아 수행된 연구임(계약번호 UC170001DD).

References

• Gururaja, T. R., Schulze, W. A., Cross, L. E., Newnham, R. E., Auld, B. A. and Wang, Y. J., 1985, Piezoelectric Composite Materials for Ultrasonic Transducer Applications. Part I: Resonant Modes of Vibration of PZT Rod-polymer Composites, IEEE Transactions on Sonics and Ultrasonics, Vol. 32, No. 4, pp. 481~498. [https://doi.org/10.1109/T-SU.1985.31623]
• Newnham, R. E., 1986, Composite Electroceramics, Ferroelectrics, Vol. 68, No. 1, pp. 1~32. [https://doi.org/10.1080/00150198608238734]
• Akdogan, E. K., Allahverdi, M. and Safari, A., 2005, Piezoelectric Composites for Sensors and Actuator Applications, IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, Vol. 52, No. 5, pp. 746~775. [https://doi.org/10.1109/TUFFC.2005.1503962]
• Auld, B. A. and Wang, Y., 1984, Acoustic Wave Vibrations in Periodic Composite Plates, IEEE 1984 Ultrasonic Symposium, pp. 528~532. [https://doi.org/10.1109/ULTSYM.1984.198353]
• Bowen, L., Gentilman, R., Fiore, D., Pham, H., Serwatka, W., Near, C. and pzaol, B., 1996, Design, Fabrication, and Properties of Sonopanel^TM 1-3 Piezocompostie Transducers, Ferroelectrics, Vol. 187, No. 1, pp. 109~120. [https://doi.org/10.1080/00150199608244847]
• Giviansky, L. V. and Torquato, S., 1997, Optimal Design of 1-3 Composite Piezoelectrics, Structural Optimization, Vol. 13, No. 1, pp. 23~28. [https://doi.org/10.1007/BF01198372]
• Robertson, D., Hayward, G., Gachagan, A. and Murray, V., 2006, Comparison of the Frequency and Physical Nature of the Lowest Order Parasitic Mode in Single Crystal and Ceramic 2-2 and 1-3 Piezoelectric Composite Transducers, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 53, No. 8, pp. 1503~1512. [https://doi.org/10.1109/TUFFC.2006.1665108]
• Lee, K. W., So, H. J., Lim, S. M., Kim, W. H. and Kim, D. Y., 2008, Development of Underwater Wide-band Acoustic Transducer using the 1-3 Piezoelectric Composite, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 18, No. 4, pp. 424~431. [https://doi.org/10.5050/KSNVN.2008.18.4.424]
• Smith, W. A. and Auld, B. A., 1991, Modeling 1-3 Composite Piezoelectrics: Thickness-mode Oscillations, IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 38, No. 1, pp. 40~47. [https://doi.org/10.1109/58.67833]