미소진동 대응 Stewart Platform 기반 Hexapod형 진동절연장치의 배치에 따른 전달률 특성 연구

1. 서 론

현대의 광학, 통신 위성의 높은 임무 수행 수준을 만족시키기 위해서는 높은 지향 안정성(pointing stability)이 요구된다. 지향 안정성을 방해하는 큰 요소 중 하나는 위성 내부에서 지속적으로 발생하는 미소진동(microvibration)이며, 위성 자세 제어를 위해 사용되는 반작용휠(reaction wheel), 제어모멘트자이로(control moment gyro), 적외성 영상 촬영을 위한 극저온 냉각기(cryocooler) 등에서 발생한다⁽¹⁾. 이러한 진동원에서 발생하는 미소진동은, 공기에 의한 감쇠가 없는 우주 환경과, 위성체의 낮은 감쇠와 맞물려 광학 탑재체와 같은 임무 장비로 전달된다. 따라서, 미소진동을 절연할 수 있는 진동절연장치(vibration isolator)를 진동원과 결합하여 진동원에서 발생하는 미소진동을 절연하는 것이 일반적이다.

위성 내부의 여러 진동원 중, 반작용휠, 제어모멘트자이로는 내부의 고속으로 회전하는 플라이휠의 불균형과, 베어링의 불규칙성에 의해 휠의 lateral mode와 whirl mode를 포함하는 6자유도(6-DOF) 교란력을 발생시킨다. 따라서 이러한 진동원에 대응하는 진동절연장치도 6자유도 진동에 대응 가능한 다축 진동절연장치가 필요하다.

위성 내부의 미소진동을 절연하기 위한 다축 진동절연장치로, honeywell에서는 점성 유체 기반 진동절연장치인 D-strut 단축 진동절연장치를 hexapod 형태로 확장하여 허블 우주 망원경의 반작용휠에서 발생하는 미소진동을 절연하는 데에 사용하였으며⁽²⁾, TRW에서는 찬드라 엑스선 관측선(chandra X-ray observatory)의 반작용휠 미소진동을 절연하기 위해 유연 커플링(flexible coupling) 형태의 스프링 요소와 점탄성 물질(VEM)을 결합한 단축 절연장치를 hexapod 형태로 확장하여 사용하였다⁽³⁾.

여러 hexapod 형태 중, Stewart platform은 6개의 스트럿(strut)을 이용하여 평행한 두 평판을 유니버셜 조인트를 통해 연결한 형태로⁽⁴⁾, 하판이 고정된 상태에서 상판의 6자유도 운동을 각 스트럿의 축 방향 운동의 조합으로 표현할 수 있기에 자세 제어를 위한 작동기(manipulator)로 사용되며⁽⁵⁾, 작동기를 포함하는 수동^(2,3), 동적⁽⁶⁾, 하이브리드 진동절연장치⁽⁷⁾로도 사용된다. Stewart platform 기반 hexapod형 진동절연장치는 단축 진동절연장치를 확장하여 구성되기에 전체 진동 절연 특성을 단축 진동절연장치의 절연 특성을 hexapod의 기하학적 배치와 결합하여 도출할 수 있는 이점이 있다.

이 연구에서는 Stewart platform 기반 hexapod형 수동 진동절연장치에 대해, Stewart platform 배치(configuration)의 기하학적 제약 조건 하에서, Stewart platform을 구성하는 스트럿의 각도 변화에 따른 방향 별 힘 전달률(force transmissibility) 변화를 분석하여 크로스 커플링을 줄일 수 있는 Stewart platform 기반 hexapod형 수동 진동절연장치의 배치를 제안하고자 한다.

2. Stewart Platform 기반 Hexapod형 진동절연장치

2.1 스트럿 배치와 힘 전달률

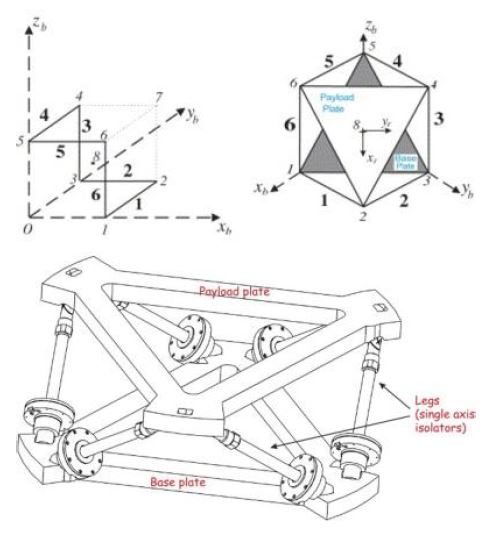
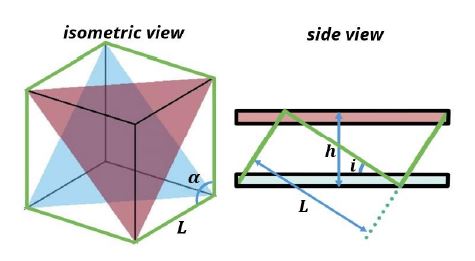
Stewart platform의 여러 배치 중, 대표적인 배치는 입방체 배치(cubic configuration)다. 입방체 배치는 Fig. 1과 같이 정육면체 상에 스트럿을 배치하는 것으로 구성되는데, 각 스트럿이 모두 90°로 만나기 때문에, 전 방향으로의 유사한 강성을 갖는 이점이 있다⁽⁶⁾. Stewart platform의 배치는 Fig. 2와 같이 아래 평판에서 만나는 스트럿 간의 각도(α)와 스트럿의 경사각(i)에 의해 결정되는데, 예를 들어 입방체 배치에서는 α는 90°, 높이 h는 $$ L/\sqrt{3}$$이므로 i는 35.26°가 된다.

Fig. 1

Stewart platform - cubic configuration

Fig. 2

Stewart platform – strut angle(α) & inclination angle(i)

Stewart platform의 배치가 결정되면, 단축 진동절연장치의 특성과 좌표 변환 행렬 J 를 이용하여, 힘 전달률을 구할 수 있다⁽⁷⁾.

관성 좌표계에서의 변위 벡터(q)와 스트럿 좌표계에서의 변위 벡터(q_s) 간의 좌표 변환 행렬 J는 식 (1)과 같이 표현할 수 있고, q = [x y z θ ϕ Ω], q_s = [q_s1 q_s2 q_s3 q_s4 q_s5 q_s6]이다.

$\[ q_s=Jq \]$

(1)

단축 진동절연장치가 높은 roll-off rate와 낮은 공진 증폭을 갖는 relaxation isolator일 때⁽⁸⁾, 힘 전달률(force transmissibility)은 식 (2)와 같다.

$\[ \begin{array}{l}\left|\frac{F_{tr}\left(s\right)}{F_d\left(s\right)}\right|\\ =\left|\begin{array}{l}{J}^{T}J\left\{c\left(k_1+k_2\right)s+k_1{k}_2\right\}\\ \times \left[M{s}^2\left(cs+k_2\right)+J^{T}J\left\{c\left(k_1+k_2\right)s+k_1{k}_2\right\}\right]\end{array}\right|\end{array} \]$

(2)

입방체 배치일 때 식 (1)에서 구할 수 있는 J^TJ 는 식 (3)과 같으며, x ↔ ϕ, y ↔ θ 방향 간의 크로스 커플링 항이 발생하는 것을 볼 수 있다.

$\[ J^{T}J=\left[\begin{array}{cccccc}2& 0& 0& 0& -L/\sqrt{3}& 0\\ 0& 2& 0& L/\sqrt{3}& 0& 0\\ 0& 0& 2& 0& 0& 0\\ 0& L/\sqrt{3}& 0& 2L^3/3& 0& 0\\ -L/\sqrt{3}& 0& 0& 0& 2L^3/3& 0\\ 0& 0& 0& 0& 0& 2L^2\end{array}\right] \]$

(3)

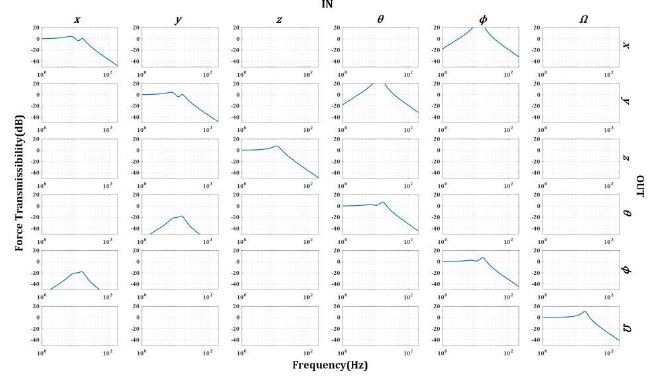
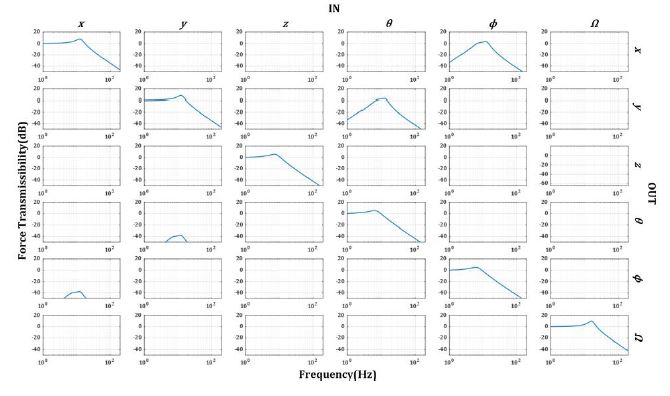
단축 진동절연장치의 주요 파라미터가 Table 1과 같을 때, 입방체 배치 hexapod형 진동절연장치의 6축 방향에 대한 힘 전달률 그래프는 Fig. 3과 같다. Fig. 1과 같은 Stewart platform은 Z축 기준 대칭을 이루기 때문에, Fig. 3의 힘 전달률 그래프에서 x → x와 y → y, θ → θ와 ϕ → ϕ, x → ϕ와θ → y와 ϕ → x의 결과는 동일하다.

Table 1

Single-axis vibration isolator parameters

Fig. 3

Force transmissibility – cubic configuration

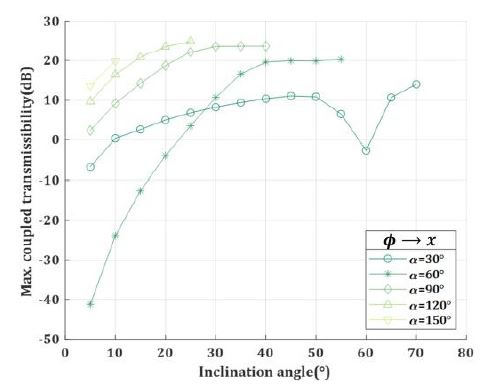
J^TJ 행렬에서는 x ↔ ϕ 그리고 y ↔ θ 의 크로스 커플링 항의 크기가 동일하지만, Fig. 3의 힘 전달률 그래프에서는 ϕ → x 방향에서 최대 20 dB가 넘는 증폭이 발생하는 데에 반해, x → ϕ 방향에서는 최대 –20 dB 정도의 감쇠가 발생하는 것을 확인할 수 있다. 따라서, 진동 절연 관점에서 관심 있는 크로스 커플링 항은 ϕ → x이며, 입방체 배치에서는 ϕ → x방향에서 크로스 커플링 항의 최대 전달률 크기가 20 dB가 넘는 것을 확인할 수 있다.

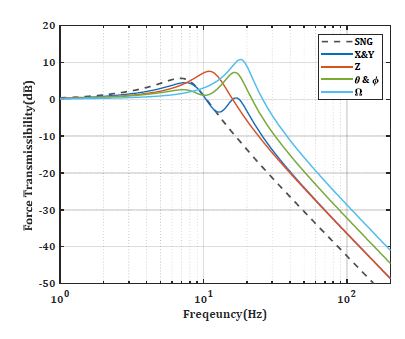
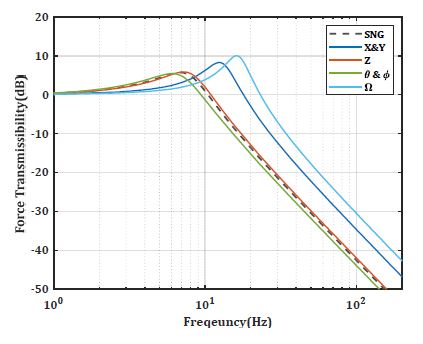
크로스 커플링 항을 제외한 대각 항(diagonal terms)의 힘 전달률 그래프는 Fig. 4와 같다. 단축 절연장치(SNG)와 비교 시 X(Y) 방향은 passband 구간의 특성이 유사하나 다소 낮은 최대 증폭값을 갖고, Z 방향은 단축 절연장치 보다 더 넓은 대역폭과 다소 높은 최대 증폭값을 갖는 것을 확인할 수 있다.

Fig. 4

Force transmissibility – cubic configuration (diagonal terms)

2.2 Stewart Platform 배치의 기하학적 배치에 따른 진동 절연 특성 분석

입방체 배치 hexapod형 진동절연장치의 힘 전달률 결과에서 확인할 수 있듯, 대각 항의 힘 전달률이 단축 절연장치와 비교 시 유사한 장점이 있지만, ϕ → x방향 크로스 커플링의 최대 증폭값이 큰 한계가 있다.

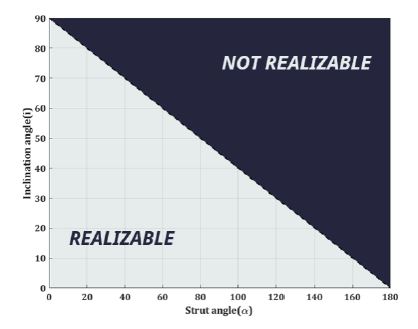
Fig. 2의 Stewart platform에서, 하판 스트럿 각도(α)와 스트럿의 경사각(i)을 바꾸면 입방체 배치 외의 다른 일반적인 배치들을 구현할 수 있는데, 기하학적 제약 조건에 의해 실제 구현 가능한 형상의 범위는 식 (4)의 조건에 의해 결정되며, 구현 가능한 형상의 범위는 Fig. 5와 같다.

(4)

Fig. 5

Stewart platform – realizable configuration

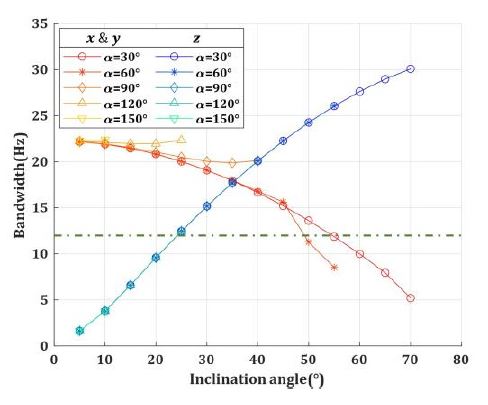
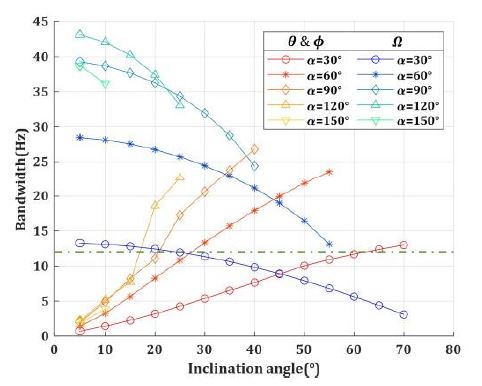
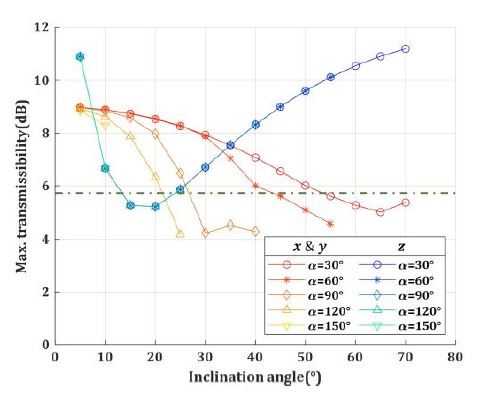
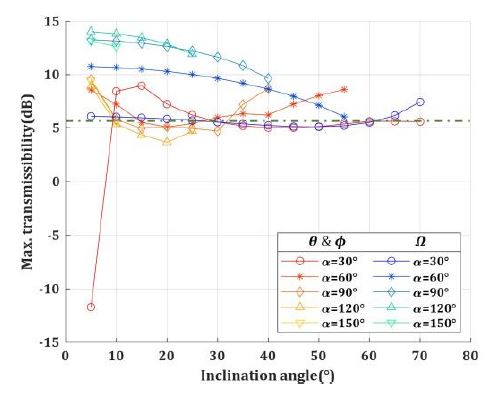
Fig. 5의 구현 가능한 형상 중, 크로스 커플링을 감소시킬 수 있는 배치를 도출하기 위해 Stewart platform에서의 하판 스트럿 각도(α)와 스트럿의 경사각(i)을 각각 30° ≤ α ≤ 150°, 5° ≤ i ≤ 70°범위에서 변화시키며 힘 전달률의 주요 지표 중 대각 항의 대역폭, 최대 전달률 크기 그리고 크로스 커플링 최대 전달률 크기를 비교하였다. 결과는 Figs. 6 ~ 10과 같으며, Figs. 6 ~ 9의 녹색 점선은 단축 절연장치의 값이다.

Fig. 6에서 보듯, Z 방향 대역폭은 하판 스트럿 각도(α)에 관계없이 경사각(i)에만 영향을 받으며 경사각이 증가할수록 증가하는 경향을 보인다. 반면, X(Y)방향 대역폭은 스트럿 경사각이 증가할수록 감소하는 경향을 보이며, 하판 스트럿 각도에 의한 변화보다, 스트럿 경사각에 의한 대역폭의 변화가 큰 것을 확인할 수 있다.

Fig. 6

Bandwidth – translational direction

Fig. 7의 θ(ϕ)방향 대역폭은 경사각(i)에 따라 증가하며 하판 스트럿 각도(α)가 증가할수록, 경사각에 따라 증가하는 대역폭의 크기가 증가한다. 반면, Ω방향은 하판 스트럿 각도에 따른 대역폭의 변화가 크고, 경사각에 따라 감소하는 경향을 보인다. 또한, Ω 방향 대역폭은 하판 스트럿 각도가 30°인 경우를 제외하면 모두 단축 절연장치보다 큰 대역폭을 갖는다.

Fig. 7

Bandwidth – angular direction

진동절연장치의 대역폭이 줄어들수록, 절연가능한 주파수 대역이 증가하나, 진동원의 정적 하중을 지지하기 위한 강성이 감소한다. 또한, 반작용휠이나 제어모멘트자이로와 같은 경우, 제어에 필요한 대역폭이 확보되지 않는 것과 같은 문제가 발생할 수 있기에, 단축 진동절연장치와 유사하거나 다소 높은 대역폭을 갖는 것이 적절하다 볼 수 있다.

Fig. 8의 Z 방향 최대 전달률 크기는 하판 스트럿의 각도(α)와 관계없이 스트럿 경사각(i)에만 영향을 받고, 스트럿 경사각 20°까지 감소하다 이후 증가하는 경향을 보인다. X(Y)방향은 스트럿 경사각이 증가할수록 감소하지만 4 dB 보다는 감소하지 않는 것을 확인할 수 있다.

Fig. 8

Max. transmissibility – translational direction

Fig. 9의 Ω방향 최대 전달률 크기는, 대역폭과 유사하게 하판 스트럿 각도가 증가할수록 증가하며 스트럿 경사각이 증가함에 따라 감소한다. 증가폭은 하판 스트럿 각도가 30°에서 60°로 증가할 때 가장 크고, 단축 절연장치의 최대 전달률 크기와 유사한 수준까지 감소하는 것을 볼 수 있다. θ(ϕ)방향 최대 전달률 크기는 하판 스트럿 각도가 증가함에 따라 감소하다 증가하며 하판 스트럿 각도가 30°인 경우를 제외하고는 유사한 경향을 보인다.

Fig. 9

Max. transmissibility – angular direction

θ(ϕ)방향에서, 하판 스트럿 각도가 30°이고 스트럿 경사각이 5°인 경우, 최대 전달률 크기가 다른 경우와 비교 시 아주 작은 값을 보이는데, 이는 대역폭이 0에 매우 가깝기 때문이다.

Fig. 10의 크로스 커플링의 최대 전달률 크기는 하판 스트럿 각도가 증가할수록 증가하며, 스트럿 경사각이 증가함에 따라 증가폭이 줄어드는 것을 확인할 수 있다. 최대 전달률 크기는 passband 방향에 관계없이 작을수록 이점이 크기 때문에, Fig. 8 ~ 10에서 보듯 하판 스트럿 각도가 90°보다 큰 경우에 진동 절연 관점에서는 큰 이득이 없는 것을 확인할 수 있다.

Fig. 10

Max. coupled transmissibility

Figs. 6 ~ 10의 결과를 고려하여, 단축 절연장치와 유사한 수준의 대역폭을 확보하고, 크로스 커플링 크기를 줄일 수 있는 배치로 하판 스트럿 각도(α)는 60°, 스트럿 경사각(i)이 25°를 선택하였고, 힘 전달률 그래프는 Figs. 11, 12와 같다. Figs. 3, 4와 비교시, 크로스 커플링(ϕ → x)의 최대 전달률 크기가 약 4 dB로 감소하였는데, 이는 단축 절연장치의 최대 전달률 크기와 유사한 수준이다. 대각 항의 힘 전달률 특성에서는 X(Y)방향과 Ω 방향의 대역폭이 단축 절연장치 대비하여 다소 증가하였지만, 입방체 배치 또한 Z 방향과 Ω 방향의 대역폭이 단축 절연장치 대비 증가하기 때문에, 감소한 크로스 커플링 최대 전달률 크기를 고려하면, Fig. 11의 결과 또한 Stewart platform 기반 절연장치에 사용되기에 적합하다 볼 수 있다.

Fig. 11

Force transmissibility – α = 60˚ & i = 25˚

Fig. 12

Force transmissibility – α = 60˚ & i = 25˚

3. 결 론

이 연구에서는 다축 미소진동 절연을 위한 Stewart platform 기반 hexapod형 진동절연장치의 배치에 따른 힘 전달률 특성 변화를 분석하였다. 먼저, 입방체 배치(cubic configuration)에 대한 방향 별 전달률 특성을 분석하고, Stewart platform에서의 기하학적 제약 조건을 이용하여, 구현 가능한 배치에 대해 하판 스트럿 각도(α)와 스트럿 경사각(i)에 따른 힘 전달률의 주요 지표 중 대각 항의 대역폭, 최대 전달률 크기 그리고 크로스 커플링 항의 최대 전달률 크기를 비교하였다. 그 중, α=60° i=25°인 배치를 선정, 크로스 커플링 항의 최대 전달률 크기가 4 dB 수준으로 감소하고 대각 항 중 3방향의 전달률 특성이 단축 절연장치와 유사한 수준으로 나타났다. 이 연구가 Stewart platform 기반 진동절연장치를 설계할 때, 6자유도 진동원의 방향성에 맞추어 설계하는 방법으로 유용하게 사용될 수 있을 것으로 기대된다.

References

• Park. G. Y., Lee. D. O., Yoon. J. S. and Han. J. H., 2014, Analytical & Experimental Study on Microvibration Effects of Satellite, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 24, No. 1, pp. 5~13. [https://doi.org/10.5050/KSNVE.2014.24.1.005]
• Davis, L. P., Wilson, J. F., Jewell, R. E. and Roden, J. J., 1986, Hubble Space Telescope Reaction Wheel Assembly Vibration Isolation System, NASA Marshall Space Flight Center, Huntsville, Alabama.
• Pendergast, K. J. and Schauwecker, C. J., 1998, Use of a Passive Reaction Wheel Jitter Isolation System to Meet the Advanced X-ray Astrophysics Facility Imaging Performance Requirements, SPIE, In Space Telescopes and Instruments V, Vol. 3356, pp. 1078~1094. [https://doi.org/10.1117/12.324508]
• Stewart, D., 1965, A Platform with Six Degrees of Freedom, Proceedings of the Institution of Mechanical Engineers, Vol. 180, No. 1, pp. 371~386. [https://doi.org/10.1243/PIME_PROC_1965_180_029_02]
• Fichter, E. F., 1986, A Stewart Platform-based Manipulator: General Theory and Practical Construction, The International Journal of Robotics Research, Vol. 5, No. 2, pp. 157~182. [https://doi.org/10.1177/027836498600500216]
• Preumont, A., Horodinca, Romanescu, I., De Marneffe, B., Avraam, M., Deraemaeker, A., and Hanieh, A. A., 2007, A Six-axis Single-stage Active Vibration Isolator based on Stewart Platform, Journal of Sound and Vibration, Vol. 300, No. 3-5, pp. 644~661. [https://doi.org/10.1016/j.jsv.2006.07.050]
• Lee, D. O., Park, G. and Han, J. H., 2016, Hybrid Isolation of Micro Vibrations Induced by Reaction Wheels, Journal of Sound and Vibration, Vol. 363, pp. 1~17. [https://doi.org/10.1016/j.jsv.2015.10.023]
• Lee, D. O. and Han, J. H., 2012, A Comparison of Vibration Isolation Characteristics of Various Forms of Passive Vibration Isolator, Proceedings of the KSNVE Annual Spring Conference, pp. 232~237.