풍하중을 고려한 대형 레이더 구동부의 구조 안전성 평가

2.1 설계 요구조건 분석

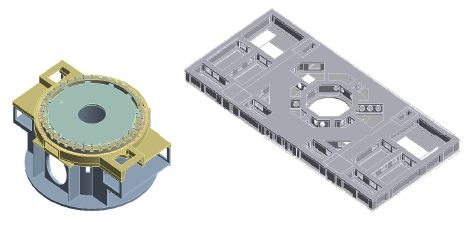
대형 레이더의 구동부는 Fig. 1과 같이 구동장치와 플랫폼으로 구성되어 있다. 구동장치의 경우, 플랫폼과 안테나를 회전시키기 위한 모터와 베어링으로 구성되어 있다. 플랫폼의 경우는 실제 안테나 부가 설치되는 곳이며, 구동부의 회전력 전달 및 정비를 용이하게 하며 안테나와 함께 360˚ 회전한다.

Fig. 1

Large radar drive system and platform

베어링은 전체 구조물과 베어링의 수명을 고려하여 결정되었으며, cross roller 타입의 slewing bearing이 선택되었다. Slewing bearing의 경우(Fig. 2 참조), 고하중 저속에 적합하며 높은 강성으로 동적하중에 대한 우수한 내구력을 가지고 있다⁽³⁾.

Fig. 2

Slewing bearing

베어링의 내륜과 외륜은 M16 볼트 체결을 통해 구동부와 플랫폼에 연결된다.

내륜의 경우, 구동부 상부의 장착판과 M16 볼트 36 EA로 체결이 되며, 외륜은 플랫폼 하부의 회전판과 M16 볼트 36 EA로 체결 및 회전을 한다.

대형 레이더의 풍하중과 관련하여 상세 요구조건은 Table 1과 같다. 대형 레이더는 운용 시 75 knot의 풍하중 조건을 견디도록 설계되어야 한다. 또한, 안테나부가 받는 하중을 계산하여 구동부의 베어링이 원활하게 작동하도록 설계하여야 한다⁽⁴⁾. 대형 레이더에 사용되는 베어링의 경우, 강성 규격에 따른 허용 가능 변형량은 다음과 같다.

Table 1

Criteria of large radar bearing deformation

풍력에 의해 안테나부에 수직으로 작용하는 압력은 수식 (1)과 같이 계산된다⁽³⁾.

여기서 C_p, ρ, υ는 각각 항력계수, 밀도, 풍속이다. 식 (2)를 통하여 안테나에 수직으로 작용하는 압력을 계산할 수 있다. 이렇게 계산된 압력 P에 주안테나의 개구면 면적인 A_A를 곱하여 안테나에 수직으로 작용하는 힘 F_A를 계산하였다.

안테나에 수직으로 작용하는 힘은 유한요소 해석 모델의 안테나 무게중심 지점에 remote force로 입력하였다^(3,5).

2.2 유한요소 해석 조건

전체 구조물에 대한 유한요소 해석은 ANSYS 2021 R2를 사용하여 진행하였다.

대형 레이더의 유한요소 해석 모델은 구동장치와 플랫폼으로 이루어져 있으며 Fig. 3과 같다. 베어링의 내륜과 외륜은 각각 36개의 M16 Bolt로 구동부와 플랫폼에 결합되어 있다. 볼트의 주요 부위에 대해서 상세 모델링을 수행하였으며, 각 볼트에 대한 bolt pretension을 구하여 해석 조건에 입력하였다.

Fig. 3

Point mass of antenna

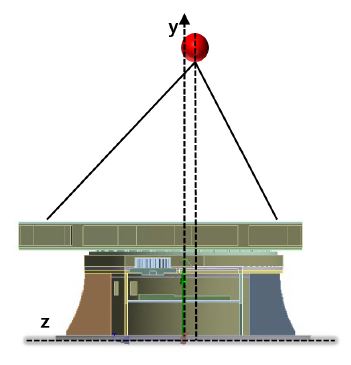
안테나의 경우, 무게중심을 고려하여 point mass로 입력하여 유한요소 해석의 모델링을 구성하였다.

무게중심과 무게를 고려한 안테나의 point mass는 아래 Fig. 4와 같이 플랫폼의 안테나 구조물과 결합되는 부분에 질량이 가해지도록 설정하였다.

Fig. 4

Force on point mass and wind load

식 (2)에서 구한 풍하중으로 인해 안테나에 가해지는 힘은 안테나의 무게중심에 가해지도록 하였고 설정된 point mass에 remote force를 입력하여, 안테나에 가해지는 풍하중을 구현하였다.

구동부와 플랫폼의 구조안전성을 확인하기 위해 입력된 풍하중과 힘은 Table 2와 같다. Table 2와 같이 50 knot에서 75 knot까지 총 4가지 조건에 대해서 풍하중을 입력하였으며, 풍하중과 함께 베어링 외륜과 상부 플랫폼, 안테나 무게중심이 5 RPM으로 일정한 속도로 회전 상황을 구현하기 위해 조화 해석(harmonic analysis)을 진행하여, 레이더의 구동에 따른 외력으로 인한 베어링의 변형량과 안전 여유도를 확인하였다.

Table 2

Input wind load

2.3 대형 레이더 구동부의 구조안전성 검증

해당 베어링의 경우, 제조사에서 제시하는 강성규격은 radial deflection의 경우 0.045 mm 이내, circumferential deflection의 경우는 0.101 mm 이내이다.

베어링의 변형량을 확인하기 위한 유한요소 해석은 3단계로 나누어 진행하였다. 볼트의 초기 장력 (pre-tension)과 안테나 무게만을 반영한 변형량을 확인하고, 이후 볼트 초기 장력과 안테나 무게가 적용된 결과값, 마지막으로 bolt pretension과 풍하중, 안테나 무게를 입력한 값을 비교 검토하였다.

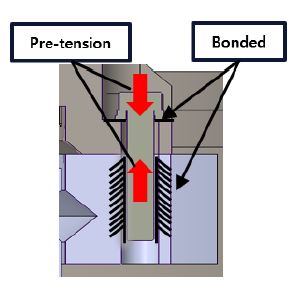
Bolt pretension의 경우, Fig. 5와 같이 M16 bolt에 스프링 와셔, 평 와셔를 모델링 및 구현하여, 92.1 kN의 체결력을 적용하였다.

Fig. 5

Boundary condition for bolt

Bolt pretension을 구현하기 위한 접촉 조건으로는 볼트의 나사산과 부품이 체결되는 부위, 와셔와 부품 간의 접촉부위에 bonded 조건을 주며, 베어링과 접촉되는 구조물에는 no separation 조건을 주어 체결력을 구현 및 해석을 진행하였다.

변형량은 베어링의 내륜의 경우, 내륜의 하부면(lower part)과 구동부와 결합되는 모서리를 확인하였다. 외륜의 경우, 외륜 상부 면(upper part)과 플랫폼 하단의 회전판과 접촉되는 부위의 모서리를 확인하였다.

내륜과 외륜에서의 radial, circumferential 방향에 대해서 확인하였다.

Bolt pretension과 안테나 자중을 입력한 경우 베어링의 변형량은 Figs. 6 ~ 9와 같으며, Table 3은 상기 bolt pretension과 안테나 자중 조건에서의 베어링의 radial, circumferential 방향의 최대 변형량이다.

Fig. 6

Radial deformation of lower part of the inner ring

Fig. 7

Circumferential deformation of lower part of the inner ring

Fig. 8

Radial deformation of upper part of the outer ring

Fig. 9

Circumferential deformation of upper part of the outer ring

Table 3

Max. deformation of bearing under antenna weight

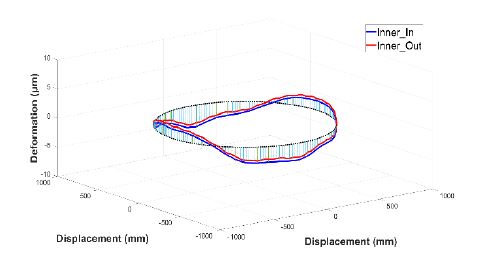
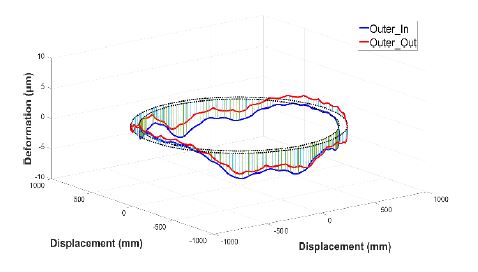
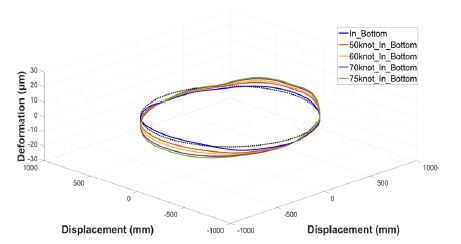
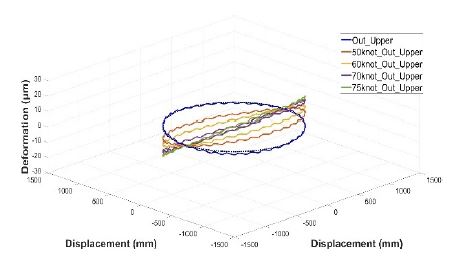
Fig. 6과 8에서의 베어링 내륜과 외륜의 radial 방향 변형량 그래프에서, 안테나의 하중으로 인한 변형을 확인할 수 있었다. 안테나 하중으로 인한 최대 변형량은 내륜의 경우, 3.74 ㎛이며 외륜의 경우 5.57 ㎛이다.

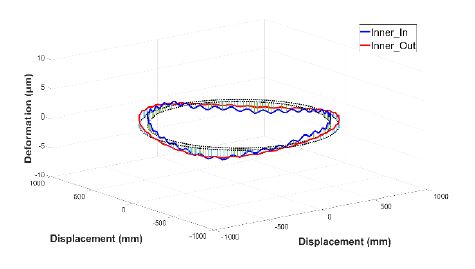
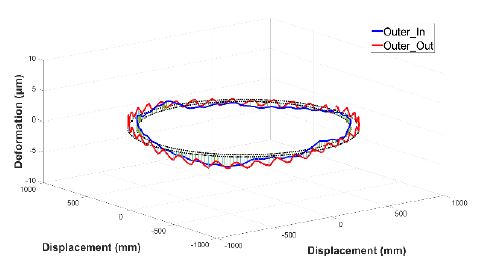
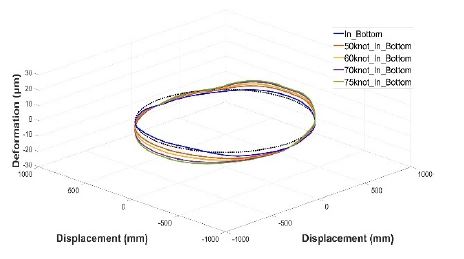
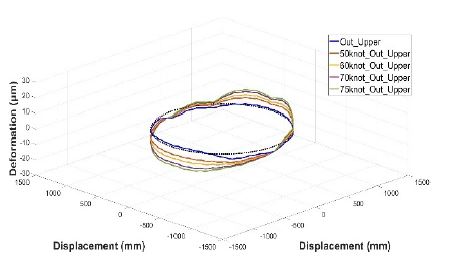
Fig. 7과 9에서는 베어링 내륜과 외륜의 circumferential 방향의 변형량에서 볼트 체결이 되어있는 부위에 대해서 bolt pretension으로 인한 변형을 확인하였다. bolt pretension에 의한 최대 변형량은 내륜의 경우 3.79 ㎛, 외륜의 경우는 2.02 ㎛인 것을 확인하였다.

Bolt pretension으로 인한 변형을 확인한 이후, 풍하중에 의한 베어링의 변형량을 확인하였다. 풍하중은 Table 2와 같이 4가지 경우를 입력하여 각각의 변형량을 확인하였다. 변형량 확인은 상기 Figs. 6, 7, 8, 9와 동일하게 내륜의 하부 면(lower part)과 외륜의 상부 면(upper part)의 접촉부 모서리에서 확인하였다. 각 풍하중에 따른 변형량은 Figs. 10 ~ 13과 같다.

Fig. 10

Circumferential deformation of lower part of the inner ring under wind load

Fig. 11

Radial deformation of lower part of the inner ring under wind load

Fig. 12

Circumferential deformation of upper part of the outer ring under wind load

Fig. 13

Radial deformation of upper part of the outer ring under wind load

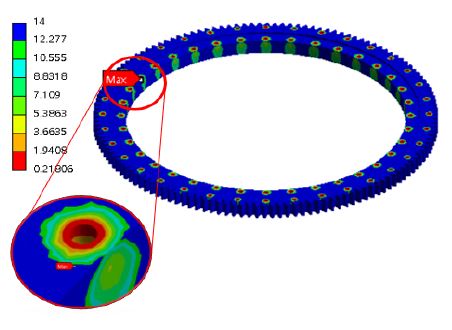
유한요소 해석 결과, 풍하중과 5 r/min의 저속 회전 상태에서 베어링은 Figs. 12, 13과 같이 내륜보다 외륜에서 변형량 변화가 더 큰 것을 확인하였다. 내륜의 경우, Figs. 10, 11과 같이 구동부와 접하는 면의 내측 모서리에서 가장 큰 변형이 발생하였고, 외륜은 상부 회전판과 접하는 면의 외측 모서리에서 가장 큰 변형이 발생하였다.

또한, 풍하중 변화에 따른 방향 별 변화로는 circumferential 방향의 변화량이 radial 방향의 변화량에 비해 최대 1.2배 더 크게 변화하는 것을 확인하였다.

Table 4는 Figs. 10 ~ 13에서의 bolt pretension과 안테나 자중, 풍하중, 저속 회전의 영향으로 인한 베어링의 전체 변형량을 정리한 것이다. Table 3의 결과와 비교하여, 풍하중이 없는 조건에서 5 r/min의 회전은 0.083 Hz의 저속 회전으로, 실제 레이더 구조물에 영향을 미치지 않는 것을 확인하였다.

Table 4

Max deformation of bearing under antenna weight and wind load

베어링의 최대 변형은 75 knot의 풍하중에서 24.8 ㎛으로 발생하였다.

또한 유한요소 해석 결과를 바탕으로 radial 및 circumferential 방향의 최대 변형량을 바탕으로 베어링의 강성 규격에 따른 허용 가능 변형량(criteria)과 비교한 값은 Table 5와 같다.

Table 5

Result of finite element model

베어링의 유한요소 해석 결과, 풍하중의 영향이 없을 경우에 radial 방향의 변형은 circumferential 방향의 변형 보다 최대 2.2배 더 높게 나오는 것을 확인하였다. 이는 Fig. 3과 같이 구동부에 결합되는 플랫폼 구조물이 y축을 기준으로 비대칭적인 형상을 지니고 있으며, 풍하중이 증가함에 안테나의 무게 중심에 작용하는 힘이 증가 및 무게 중심의 이동으로 인한 영향을 크게 받는 것을 확인하였다. 또한, 풍하중을 고려한 경우, circumferential 방향의 변형이 radial 방향의 변형보다 더 큰 영향을 받게 된다.

구조물의 내구성 및 구조안전성 평가 시에 많이 사용되는 안전 여유도(M.S : margin of safety)를 등가응력으로 확인하였다. 안전 여유도는 식 (3)과 같이 계산하였으며, 대형 레이더의 베어링 재질의 항복강도 대비 작용하는 응력의 비율로 계산하였다. 계산된 안전 여유도가 0보다 크면 구조물이 안전한 것으로 판단할 수 있다. 베어링의 재질은 aluminum 4150 H이며, 항복강도는 380 MPa로 안전여유도를 확인하였다.

안전 여유도를 계산 시에 필요한 안전계수(factor of safety)는 구조물에 작용하는 하중의 불확실성을 고려하여 안전율 1.5를 사용하였다⁽⁶⁾. 베어링에 작용하는 최대 등가 응력을 기준으로 안전 여유도를 계산하였다.

베어링 내륜이 구동부와 접합되는 하부 면(lower part)에서 가장 낮은 안전 여유도를 확인하였다. 해당 부위의 안전 여유도 최소값은 0.218이며 내륜을 비롯하여 외륜에 대해서 안전 여유도가 0보다 높은 값으로 계산되었다. 따라서 저속 회전과 풍하중 환경에서 베어링이 안전한 것으로 판단할 수 있다(Fig. 14 참조).

Fig. 14

Margin of safety distribution of large radar