일반 절대위치 인코더를 이용한 회전진동 측정에 관한 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
A convenient process to measure the rotational vibration of a shaft in a mechanical or electrical rotating system using an ordinary absolute encoder is introduced. The output voltage signal from the encoder is sampled at an appropriate rate with a data recorder. The variation in angular position of the shaft at each time step is calculated based on the output voltage of the encoder. The angular speed of the shaft for a specific time step is then calculated by dividing the angular displacement by the corresponding time interval. The frequency components of the rotational vibration are calculated from the frequency analysis of the series of angular speeds. The validity of this process is examined via computer simulations and simple experiments, showing relatively good correspondence. The proposed method exploits the simple and convenient rotational speed measurement system using an absolute encoder and data recorder. The test results confirm that the proposed method can effectively measure the rotational vibration of a rotating machine with reasonable accuracy.
Keywords:
Absolute Encoder, Rotational Vibration, Vibration Measurement, Rotational Order, Universal Joint키워드:
절대위치 인코더, 회전진동, 진동 측정, 회전차수, 유니버설 조인트1. 서 론
회전하는 기계 또는 전기 시스템에서 자주 발생하는 각속도의 변동 즉, 회전진동 또는 비틀림진동은 시스템의 성능에 영향을 미치는 동시에 과도한 진동은 시스템의 내구성을 저하시키는 문제점을 발생시킨다. 따라서, 비틀림 진동 측정은 전력 산업(1~3)과 자동차(4~6)를 포함한 다양한 응용 분야에서 회전 장비의 분석과 진단에 중요하다. 이와 같은 학문적, 산업적 요구에 대응하기 위해서는 해당 시스템에서 발생되는 회전진동 또는 비틀림진동을 측정할 수 있는 기술이 필수적이며, 효과적인 비틀림 측정 기법을 개발하기 위하여 상당한 양의 연구가 다양한 방법으로 수행되어왔으며 다양한 체계를 만들어냈다. 현재까지 제시된 방법에는 레이저(7,8), 각도 가속도계(9) 및 시간 통과 인코더 기반 방법(10~12) 등이 있으며 최근 많은 응용 프로그램에 인코더를 기반으로 하는 방법이 많이 활용되고 있다. 인코더는 증분형 인코더와 절대위치 인코더 등 두 종류로 크게 분류된다. 증분형 인코더는 특정한 기준 위치 없이 축의 회전에 따라 펄스 열을 출력한다. 반면, 절대위치 인코더는 미리 설정된 회전축 상의 위치를 기준으로 회전각이 변화하면 변화량에 따른 전압을 출력한다.
증분형 인코더를 이용하여 회전진동을 측정하는 방법은 종래에 여러 공학자들에 의해 연구되어 왔으며 개발 기술을 이용한 상용 제품도 출시되어 있다(13~15). Nam 등(13)은 상용화 되지 않고 있는 기준기급 회전진동 센서를 대체하여 고정밀 회전 인코더를 이용한 회전진동 교정시스템의 구축이 가능함을 실험적으로 규명하였다. Resor 등(14)은 증분형 인코더를 이용하여 회전진동을 측정하는 과정에서 발생 가능한 여러 오차들을 검토하고 이들을 보상하는 기술을 소개하였다. 그러나 절대 위치 인코더를 이용한 회전진동 측정에 관한 연구는 충분한 연구가 이루어지지 않아 관련 문제점과 개선 방안에 대한 검토도 충분치 않다.
이 연구에서는 절대 위치 인코더를 이용하여 회전진동을 측정하는 방법을 제시하고 관련 문제점과 개선 방안을 검토한다. 아울러 universal joint를 통해 의도적으로 회전축에 도입된 회전진동을 제시된 방법을 통해 측정한 다음 그 결과를 이론적인 값과 비교하여 제시된 방법의 정확도를 검증한다. 이 논문의 구성은 다음과 같다. 2장에서는 절대위치 인코더를 이용하여 축의 회전수와 회전진동을 측정하는 방법에 대해 기술한다. 3장에서는 이 연구에서 제안한 방법을 검증하기 위한 실험 구성과 실험 결과에 대해 기술하며 4장에서는 결론을 맺는다.
2. 절대위치 인코더를 이용한 회전진동 계측 방법
이 장에서는 상용 절대위치 인코더를 이용하여 회전수 측정 원리와 회전진동을 측정하는 방법에 대해 검토한다. 이 연구에서 검토하는 상용 절대 위치 인코더의 예가 다음 Fig. 1에 설명되어 있다. 절대위치 인코더는 정해진 기준 위치에서 회전하는 각도에 비례하는 전압을 출력하는 특성을 가지고 있으며 이와 같은 특성을 이용하여 회전수와 회전진동을 측정하는 방법을 설명한다.
2.1 회전수 측정
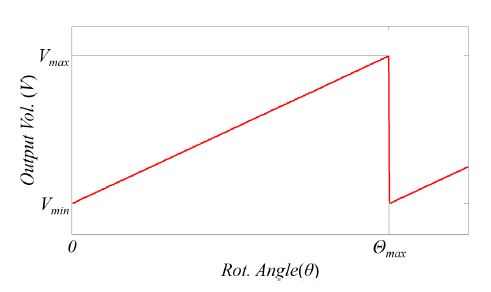
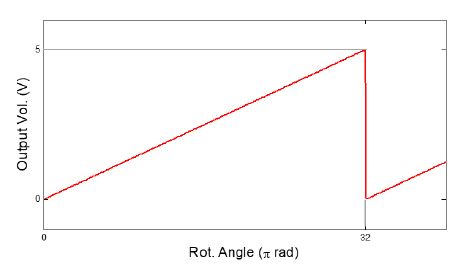
이 연구에서 사용되는 회전수 측정 시스템은 회전축에 널리 적용되고 있는 일반 상용 절대위치 인코더 (absolute encoder)이다. 먼저 비접촉방식의 회전수 측정 시스템의 원리를 간단히 기술한다. 절대위치 인코더는 종류에 따라 축 회전각도에 비례하는 전압을 발생시킨다. 특별한 외란이나 진동이 없는 상태에서 일정한 속도로 회전하는 회전축의 경우 인코더에서 발생되는 전압 출력이 Fig. 1에 설명되어 있다.
그림에서 보는 바와 같이 인코더의 출력 전압은 축의 회전각에 비례하여 증가하며 미리 정해진 최대 회전각(θmax)에 도달하면 최대전압(vmax)을 나타낸다.
축의 회전수는 삼각 펄스의 개수를 관측하여 측정할 수 있으며 펄스 중간 위치에서의 회전수는 해당 위치에서의 전압을 이용하여 계산할 수 있다.
2.2 회전진동 측정 기술
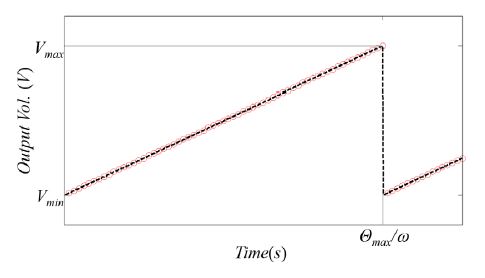
이 절에서는 Fig. 2에 설명되어 있는 것과 같은 삼각 pulse를 발생하는 절대위치 인코더를 이용하여 추가적인 센서 장착없이 회전축에 발생하는 회전진동을 측정하는 방법에 대해 기술한다.
Fig. 2과 같은 출력 특성을 나타내는 절대위치 인코더를 이용하여 회전진동을 측정하기 위해서는 우선 다음 Fig. 3과 같이 인코더에서 출력되는 아날로그 신호를 정해진 시간 간격으로 sampling하여 분산, 디지털 신호로 수집해야 한다.
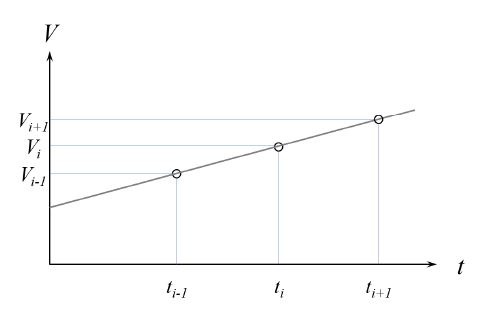
일정한 속도로 회전하는 축에 인코더를 장착한 경우 그래프 상의 각 측정 점들을 연결한 직선은 동일한 기울기를 나타낸다. 그러나 축의 회전속도가 변동하는 경우, 기울기가 시간에 따라 변동하게 되고 이 변동을 분석하면 ‘회전속도의 변동’ 즉, 회전진동을 계산할 수 있다. Fig. 4에 인코더에서 출력되는 전압신호를 정해진 sampling rate(fs)로 측정한 결과를 설명하였다. 회전진동(rotational vibration: R.V.)이 존재하지 않는 경우 그림 상 각 sampling 점에서의 직선의 기울기는 동일하게 나타나지만 그렇지 않은 경우에는 각 점에서 기울기는 변동하게 되며 이를 이용하여 회전진동을 측정할 수 있다.
Fig. 4에서 세 측정점에서 축의 회전각 θi과 측정점 사이의 각 변위 ∆θi는 식 (1)과 같이 구할 수 있다.
| (1a) |
| (1b) |
일정한 시간 간격으로 sampling하였으므로 각 측정점 사이의 시간간격이 ∆t(=ti+1-ti)는 일정하며 각 시간에서의 각속도는 식 (2)와 같이 구할 수 있다.
| (2) |
따라서, 앞의 과정을 각 시간 위치에서 반복 수행하면 시간에 따른 각속도의 변동을 파악할 수 있다. 또한 이 각속도 시간열에 대해 주파수 분석을 실시하면 회전진동에 포함된 주파수 성분을 분석할 수 있다.
이 절에서는 computer simulation을 이용하여 앞 절에서 소개된 측정 프로세스의 타당성을 검증한다. 이 검증에서 회전축은 명목회전수에 덧붙여 1차 및 2차 회전진동을 가지고 있어 축의 회전속도는 식 (3)과 같이 나타난다고 가정하였다.
| (3) |
여기서 Ω0는 축의 명목 회전속도이며 Ω1와 Ω2는 각각 축에 발생하는 1차 및 2차 회전진동의 크기이다. 해당 축의 회전각도는 식 (3)을 시간에 대해 적분해서 식 (4)와 같이 구할 수 있다.
| (4) |
축에 부착된 인코더는 상기 식에 의해 구해진 회전각도가 θmax만큼 증가할 때마다 1회씩 삼각 pulse가 발생하게 된다.
이와 같은 인코더의 출력의 특성을 이용한 축의 회전진동 측정 process의 타당성을 컴퓨터 시뮬레이션을 이용하여 검토하였다. 검증을 위한 시뮬레이션에 사용되는 회전축, 인코더 및 data recorder의 조건은 위에 설명된 가정을 고려하여 Table 1과 같이 설정하였다.
또한, 인코더의 불완전성을 고려하기 위하여 인코더의 입출력 과정에 1 %의 랜덤 오차가 발생한다고 가정하였다.
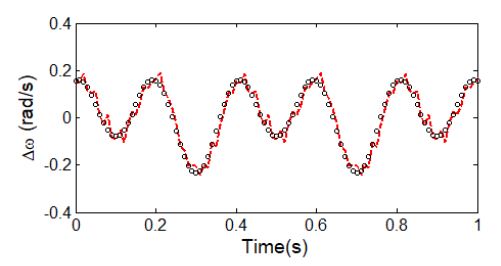
Table 1에 주어진 조건 하에서 절대위치 인코더에서 출력되는 출력 전압을 이용하여 계산된 각속도 변동과 식 (3)에 주어진 것과 같은 회전축에 의도적으로 도입한 각속도 변동을 Fig. 5에 서로 비교하였다.
Fig. 5에서 보는 바와 같이 의도적으로 도입된 ∆ωi와 측정을 simulation한 ∆ωi가 각 시간 간격에서 잘 일치하고 있음을 알 수 있다. 또한 이렇게 구해진 각속도 변동에 대해 주파수분석을 실시한 결과를 Fig. 6에 설명하였다.
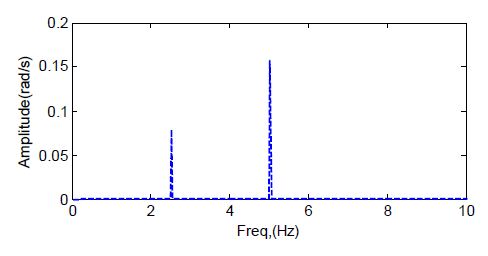
Fig. 6에서 보는 바와 같이 의도적으로 회전진동을 도입한 1차(2.5 Hz)와 2차(5.0 Hz) 성분의 회전진동이 명확히 나타남을 알 수 있다. 아울러, 시뮬레이션에서 얻어진 해당 성분의 진동의 크기를 Table 2에 이론적인 값과 비교하여 설명하였다.
Table 2에서 보는 바와 같이 1차 및 2차 성분의 크기가 의도적으로 도입한 이론적인 크기와 정확히 일치하고 있음을 알 수 있다.
따라서, Fig. 5의 시간 영역 데이터와 Fig. 6 및 Table 2의 주파수 영역 데이터 분석 결과를 바탕으로 절대위치 인코더의 출력 신호를 sampling하여 회전진동을 측정하는 방법은 충분한 정확도를 가진다고 할 수 있다.
3. 진동 변위의 계측 실험
이 장에서는 앞 장에서 제시된 방법을 적용하여 회전축에 발생하는 회전진동을 측정하는 실험을 수행하고 그 결과를 이용하여 이 연구에서 제시하는 회전진동 측정방법을 검증한다.
3.1 시스템 구성
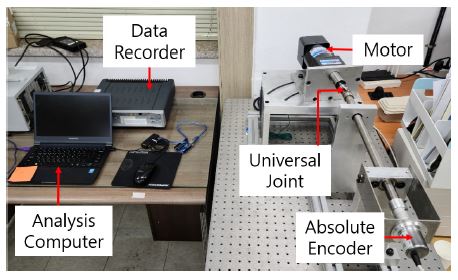
회전수 및 진동 측정을 위한 실험 시스템은 다음 Fig. 7과 같이 회전축을 universal joint로 연결된 모터를 통해 구동하는 형태로 구성되어 있다. 구동축의 끝단에는 회전속도 측정을 위한 절대위치 인코더가 부착되어 있다.
그림의 인코더는 POSITAL 사의 MCD-AC005-0412-M100-CAW 모델이며(16), 회전각도에 따른 전압 출력 특성은 다음 Fig. 8과 같이 축이 16회전하는 동안 출력전압이 0 V에서 5 V로 상승한다.
인코더 출력신호는 LMS Test Lab. 장비를 이용하여 51 200 Hz의 sampling rate, 16 bit 분해능으로 sampling하였다. 이렇게 수집된 신호는 축의 회전과 무관한 전기적인 잡음(noise)을 제거하기 위하여 적절한 저역필터(low pass filter)를 통과시킨 다음 분석한다. 각 시간 step에서의 회전각과 회전속도를 계산한다.
3.2 Universal Joint에 의한 회전진동
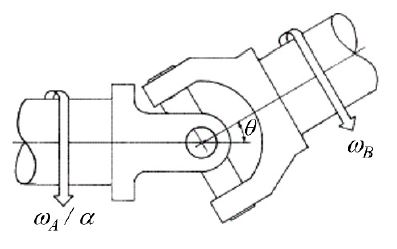
Universal joint는 주어진 각도(θ)로 교차하는 두 축 사이에서 구동력(torque)을 전달하기 위하여 사용된다(17,18). 간단한 single universal joint의 예가 Fig. 9에 설명되어 있다 그림에서 구동축(A)와 피동축(B)은 각 θ로 교차하고 있다.
기구학적인 원리에 따라 구동축의 회전속도(ωA)와 피동축의 회전속도(ωB) 사이에는 식 (5)와 같은 관계가 성립한다(17,18).
| (5) |
여기서 α는 구동축의 회전각이다. 따라서, 두 축의 회전 속도비(ωB/ωA)는 구동축의 회전각에 따라서 1회전 당 2회의 주기로 변동하며 최대값과 최소값은 각각 식 (6)과 같이 나타난다(17,18).
| (6a) |
| (6b) |
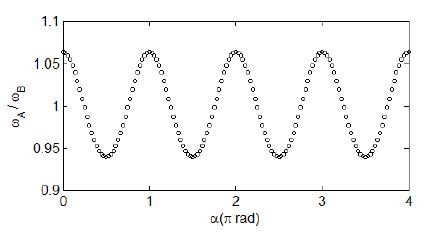
식 (5)를 이용하여 θ가 20°인 경우에 대하여 α와 ωB/ωA사이의 관계를 나타낸 그래프가 Fig. 10에 설명되어 있다.
Fig. 10에서 보는 바와 같이 ωB는 ωA의 약 94 % ~ 106 %의 범위에서 1회전 당 2회의 주기를 가진 조화함수 형태로 변동하고 있음을 알 수 있다.
3.3 실험 결과
앞 절에서 설명한 실험 장치와 process를 이용하여 회전축의 진동을 측정한 결과를 분석하여 이 연구에서 제안하는 절대위치 인코더를 이용한 회전진동 측정법의 타당성을 검토한다. 이 연구에서는 모터 축과 피동축 사이의 교차각(θ)을 각각 0° 및 20°로 설정한 다음 실험을 수행하였다.
θ가 0°인 경우에 대한 시험 결과가 Fig. 11에 설명되어 있다. 이론적으로 축의 교차각이 0°인 경우에는 universal joint 효과로 나타나는 2차 order 회전진동이 나타나지 않아야 한다.
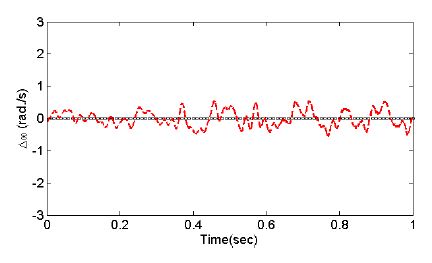
Time data for the variation in the rotational speed of the driven shaft when θ=0° (key: ◦ ◦: Theoretical, ‑ ‑: Encoder)
Fig. 11에서 보는 바와 같이 이 경우에는 2차 회전진동이 거의 나타나지 않음을 알 수 있다. 그러나 회전 부품의 불평형 질량, 회전 축의 정렬 불량, 베어링 또는 감속기 기어 불량 등 실험장치의 불완전성 등으로 인한 불규칙적인 진동이 발생하고 있음을 알 수 있다. 다음으로 θ가 20°인 경우에 대한 시험 결과가 Fig. 12에 설명되어 있다. 이 경우에는 기구학적인 특성으로 명목각속도의 약 6 %의 진폭을 가지는 회전진동이 발생하여야 한다.
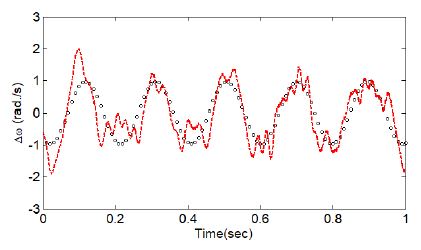
Time data for the variation in the rotational speed of the driven shaft when θ=20° (key: ◦ ◦: Theoretical, ‑ ‑: Encoder)
Fig. 12에서 보는 바와 같이, θ가 20°인 경우에 대한 결과에서 universal joint에 의해 발생되는 2차 회전진동이 지배적으로 나타지만, 앞에서 설명한 다양한 원인에 의한 회전진동 등이 추가됨으로 인해 복잡한 진동 형태를 나타내고 있음을 알 수 있다. 또한, 그림에서 보는 바와 같이 2차 order 진동의 진폭이 기구학적 특성에 의해 유도되는 진폭과 거의 유사하게 나타나고 있음을 알 수 있다.
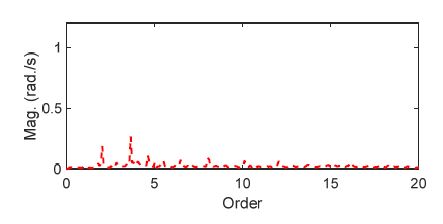
다음으로 이와 같은 시간영역의 데이터에 대한 주파수 분석을 통해 회전진동에 포함된 각각의 order 성분을 파악하였다. 주파수 분석 과정에서 time window(T)는 5초, averaging은 4회로 설정하였다. 우선 θ가 0°인 경우에 대한 분석 결과를 Fig. 13에 표시하였다.
그림에서 보는 바와 같이 뚜렷한 지배적인 성분은 나타나지 않았으나 크기가 작은 여러 차수의 진동이 복합적으로 나타남을 알 수 있다. 이러한 진동은 앞에서 설명한 실험장치의 불확실성에 기인한 진동으로 판단된다.
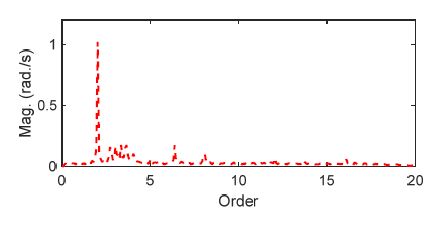
다음으로 θ가 20°인 경우에 대한 주파수분석 결과를 Fig. 14에 설명하였다.
그림에서 보는 바와 같이 축 회전 2차 성분의 진동이 크게 증가하였으며 여타 차수의 진동은 큰 차이없이 거의 동일하게 나타남을 알 수 있다. 또한 2차 성분의 크기는 1.0 rad/s로 축의 명목 회전속도의 6 %로 나타나 이론적으로 universal joint에 의해 유도되는 회전진동의 진폭과 거의 동일하게 나타남을 알 수 있다.
4. 결 론
이 연구에서는 회전수 측정을 위해 널리 사용되는 절대위치 인코더가 축의 회전 각도에 비례하는 전압을 발생시키는 출력 특성을 이용하여 회전체에 발생한 회전진동을 측정하는 방법에 대해서 검토하였다. 출력 전압을 sampling한 digital 신호를 이용하여 각 시간 step에서 축의 회전각도와 회전속도를 추출하고 이를 기반으로 회전축의 각속도 변동 즉, 회전진동을 측정한다. 또한 각속도 변동에 대한 주파수분석을 통해 회전진동의 주파수성분과 그 크기를 파악한다.
우선, 시뮬레이션을 통해 제시된 측정법의 정확도를 검증하고 인코더에 나타날 수 있는 기계적 오차의 영향도 분석하였다. 검증 결과에 따르면, 제시된 방법은 축의 회전속도의 특성에 따라 적절한 분석 파라미터를 적용하면 충분한 정확도를 가지고 회전진동 측정할 수 있음을 확인하였다.
실험을 통한 검증에서는 회전축을 universal joint로연결된 모터를 통하여 구동함으로써 축의 교차각에 따라 변동하는 2차 order 회전진동을 의도적으로 발생시키고 이를 이 연구에서 제시된 방법을 통하여 측정 분석함으로써 제시된 방법의 정확도를 확인하였다. 실험장치의 불확실성으로 인하여 universal joint를 통해 유도된 회전진동 외에 다른 성분의 진동이 포함되어 나타나지만 joint를 통해 의도적으로 도입된 2차 성분의 회전진동이 충분한 정확도로 측정됨을 시간 및 주파수 영역 분석 결과로 확인하였다.
향후, 연구에서는 회전진동을 측정하는 정확한 장비를 적용하여 이 연구에서 제시된 방법을 추가로 검증할 예정이다. 아울러, ‘증분형 인코더’ 등 다른 타입의 인코더를 이용한 회전진동 측정 검토, 이 논문의 결과와 비교 및 장, 단점 분석 등도 후속 연구에서 진행할 예정이다.
Acknowledgments
이 논문은 2020학년도 경북대학교 연구년 교수 연구비에 의하여 연구되었음.
References
- Maynard, K. P. and Trethewey, M. W., 2000, On the Feasibility of Blade Crack Detection through Torsional Vibration Measurements, Noise and Vibration Worldwide, Vol. 31, pp. 9~15.
-
Diangui, H., 2000, Experiment on the Characteristics of Torsional Vibration of Rotor-to-stator Rub in Turbomachinery, Tribology International, Vol. 33, pp. 75~79.
[https://doi.org/10.1016/S0301-679X(00)00029-3]

-
Sza´sz, G. and Guindon, E. J., 2003, Using Torsional Vibration Spectra to Monitor Machinery Rotor Integrity, Proceedings of the ASME 2003 International Joint Power Conference, ASME Paper No. IJPGC2003-40162, Atlanta, GA, USA.
[https://doi.org/10.1115/IJPGC2003-40162]

-
Citron, S. J., O’Higgins, J. E. and Chen, L. Y., 1989, Cylinder by Cylinder Engine Pressure and Pressure Torque Waveform Determination Utilizing Speed Fluctuations, SAE Paper No. 890486.
[https://doi.org/10.4271/890486]

-
Rouston, R. L., Starkey, J. M., Wang, P. and Davies, P., 1992, Torsional and Translational Vibrations of a Drive Shaft with a Cardan Joint, Proceedings of ASME 1992 Design Technical Conferences, pp. 533~542.
[https://doi.org/10.1115/DETC1992-0422]

-
Remond, D., 1998, Practical Performance of High-speed Measurement of Gear Transmission Error or Torsional Vibrations with Optical Encoders, Measurement Science and Technology, Vol. 3, No. 9, pp. 347~353.
[https://doi.org/10.1088/0957-0233/9/3/006]

-
Halliwell, N. A., Pickering, C. J. D. and Eastwood, P. G., 1984, The Laser Torsional Vibrometer: A New Instrument, Journal of Sound and Vibration, Vol. 93, pp. 588~592.
[https://doi.org/10.1016/0022-460X(84)90427-9]

-
Li, X., Qu, L., Wen, G., and Li, C., 2003, Application of Wavelet Packet Analysis for Fault Detection in Electro-mechanical Systems based on Torsional Vibration Measurement, Mechanical Systems and Signal Processing, Vol. 17, No. 6, pp. 1219~1235.
[https://doi.org/10.1006/mssp.2002.1517]

-
Seidlitz, S., 1992, Engine Torsional Transducer Comparison, SAE Paper No. 920066.
[https://doi.org/10.4271/920066]

-
Fu, H. and Yan, P., 1993, Digital Measurement Method on Rotating Shaft Torsional Vibration, Proceedings of ASME 1993 Design Techical Conferences, pp. 271~275.
[https://doi.org/10.1115/DETC1993-0202]

-
Wang, P., Davies, P., Starkey, J. M. and Rouston, R. L., 1992, A Torsional Vibration Measurement System, IEEE Transactions on Instrumentation and Measurement, Vol. 41, No. 6, pp. 803~807.
[https://doi.org/10.1109/19.199411]

-
Hernandez, W., Paul, D. and Vosburgh, F., 1996, On-line Measurement and Tracking of Turbine Torsional Vibration Resonances using a New Encoder based Rotational Vibration Method (RVM), SAE Transactions, Vol. 105, pp. 116~123.
[https://doi.org/10.4271/961306]

-
Nam, S., Baik, K. and Cheung, W., 2014, Calibration System for Angular Vibration using Precision Rotary Encoder, The Journal of the Acoustical Society of Korea, Vol. 33, No. 1, pp. 31~39.
[https://doi.org/10.7776/ASK.2014.33.1.031]

-
Resor, B. R., Trethewey, M. W. and Maynard, K. P., 2005, Compensation for Encoder Geometry and Shaft Speed Variation in Time Interval Torsional Vibration Measurement, Journal of Sound and Vibration, Vol. 286, pp. 897~920.
[https://doi.org/10.1016/j.jsv.2004.10.044]

- DEWESoft, 2000, Rotational and Torsional Vibration Measurement and Analysis.
- Posital Fraba, 2009, User Manual for Absolute Ixarc Magnetic Rotary Encoder with Analog Interface, pp. 250~255.
- Guo, Y., Sun, Z. and Zhonghong, S., 2008, The Kinematics Analysis on Single Cross Universal Joint, Proceedings of 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China.
-
Petrescu, F. I. T. and Petrescu, R. V. V., 2019, The Structure, Geometry, and Kinematics of a Universal Joint, Independent Journal of Management & Production, Vol. 10, No. 8, pp. 1713~1724.
[https://doi.org/10.14807/ijmp.v10i8.923]


Hyeong-Ill Lee Ph. D. in mechanical engineering and Professor in the School of Automotive Engineering, Kyungpook National University. Prof. Lee is teaching Dynamics, Automatic Control and Mechanical Vibration, etc. He has academic interests in automotive NVH, Brake squeal, Sound radiation from vibrating structures, etc.