설계변수감소 위상최적설계기법을 활용한 자동차용 캘리퍼 강성 최대화 설계

2.1 기존 위상최적설계기법

위상최적설계의 궁극적인 목적은 설계 영역에서 주어진 재료로 최적의 형상을 찾는 것이다. 최적의 재료 분포를 찾기 위해서는 설계영역을 유한 요소로 나누고, 하나의 요소를 하나의 설계 변수(desgin variable; ρ_i)로 고려한다. 설계 변수는 0~1의 범위로 정의되며 0의 경우는 재료가 존재하지 않는 영역, 1의 경우 재료가 존재하는 영역이다. 효율적인 수치계산을 위해 다양한 설계 변수의 모델들이 있으며, 이 연구에서는 가장 많이 사용되는 모델 중 하나인 SIMP(Solid isotropic material with penalization)⁽⁷⁾ 모델을 사용하였다(식 (1)).

E_i 는 i-번째 설계 변수의 값에 따른 인공적인 탄성계수이며, E₀는 주어진 고유의 탄성계수 값이다. 이 연구에서 n의 값은 3으로 선정하였다.

자동차용 캘리퍼의 성능 향상을 위해 강성 최대화를 고려하였으며, 강성의 역수인 컴플라이언스 최소화를 목적함수로, 부피를 제약함수로 정의하였다(식 (2)).

여기서 ψ는 컴플라이언스이며, ρ_i(x)는 i번째 설계변수이다. υ_i는 i번째 설계변수의 체적을 표현하고 있다. V_max는 부피 제한조건이다. 설계 변수가 존재하지 않는 상태는 수치적으로 0이지만, 수치적 특이점을 피하기 위해서, ρ_min의 값을 정의하며 이 연구에서는 0.01로 선정하였다. N은 설계 변수의 수이다.

정확하고 빠른 최적 조건을 찾기 위해 설계 민감도를 계산하였으며, 민감도의 정확도를 검증하기 위해 0.1 % 섭동(perturbation)을 적용한 유한차분법 결과값을 비교하였다. 또한, 잘 알려진 수치적 문제점 체커보드패턴(chekerboard pattern) 및 메쉬종속(mesh-dependence)을 극복하기 위해 설계민감도 필터링 기법을 적용하였다⁽⁸⁾.

RDVM 위상최적설계와 차이점을 설명하기 위해서는 기존 설계 변수 기반의 위상최적설계의 수렴 조건 설명이 필요하다. 기존 위상최적설계 수렴 조건은 식 (3)이 가장 보편적으로 적용된다.

여기서 ρ_i,l-1과 ρ_i,l은 각각 l-1번째 및 l번째 축차과정에서 i번째 설계 변수의 값이다. 즉, 모든 축차 과정에서 동시에 모든 설계 변수가 현재 축차(l)와 직전 축차(l-1)의 차이가 특정값(ϵ) 이하일 때만 축차과정이 끝난다. 기존 위상최적설계에서는 설계 변수 수는 모든 축차과정에서 고정값으로 동일하다. 이 연구에서는 수렴 조건의 값으로 ϵ은 0.01로 정의하였다.

2.2 RDVM 위상최적설계기법

이 연구에서는 RDVM 위상최적설계의 범용성을 위한 연구로 실제 문제인 자동차용 캘리퍼설계에 적용하였다. RDVM 위상최적설계에 대한 상세한 개념과 수식은 참고문헌 (5), (6)을 참고하길 바라며, 여기서는 기존 위상최적설계와 기본적인 차이점만 간략하게 서술하도록 하겠다.

위상최적설계 기법 적용을 위해 설계영역이 요소로 나누어지고, 기계 구조물의 경우 성능을 확인하기 위해 유한요소기법(FEM)이 적용되고 있다. 특히, 실제 문제의 경우 많은 수의 요소가 필요로 하게 되며 이는 컴퓨팅 계산 시간이 오래 걸리는 결과를 야기한다. 또한, 설계영역에서 최적의 형상을 찾기 위해 많은 축차가 필요하게 되어 오랜 컴퓨팅 시간이 필요하며, 이는 수렴 조건을 잘 정의하는 것이 매우 중요하다.

RDVM 위상최적설계는 새로운 개념의 수렴 조건을 제시하여 기존 위상최적설계를 적용하여 얻은 결과값을 빠른 시간 내에 얻는 것을 목적으로 한다. 궁극적으로 기존 위상최적설계의 단점인 컴퓨팅 계산 시간 한계를 극복하고자 하는 것이다.

기존 위상최적설계의 경우 모든 설계 변수의 변화량이 동일 축차 과정에서 식 (3)을 만족하여야 위상최적설계 과정이 마무리된다. 하지만, RDVM 위상최적설계 기법은 식 (3)을 만족하는 설계 변수의 경우는 다음 축차에서 고려하지 않고, 해당 축차에서 식 (3)을 만족하지 않은 설계 변수만을 다음 축차에서 고려하는 것이다. 처음 축차과정에서는 기존 위상최적설계 설계 변수(N)의 수 와 동일하지만, 축차과정이 진행됨에 따라 RDVM 위상최적설계의 설계 변수(NDV)의 수는 점진적으로 또는 기하급수적으로 줄어드는 과정이다. RDVM 위상최적설계의 수렴조건은 설계 변수(NDV)가 0가 되는 것이다. 이렇게 고려해야 할 설계 변수가 줄어듬에 따라 축차 수도 줄어들어 컴퓨터 계산 시간을 절약할 수 있다.

설계 변수의 수렴 상태에 따라 NDV의 수가 조절되는데, 지금까지의 축차 과정의 설계 변수를 기반으로 평균값과 표준편차를 기반으로 계산된다. 설계 변수의 평균값 계산을 위한 샘플링 수를 NSD로 정의하며, 표준편차의 값이 ϵ_r,d 보다 작은 경우 수렴된 것으로 판단하여 다음 축차부터는 설계 변수로 고려하지 않게 된다.

RDVM 위상최적설계의 목적은 빠른 수렴으로 축차 수를 최소화 하는 것인데, NSD의 수를 감소시켜 추가적인 컴퓨팅 계산 시간을 줄이는 것이다. 이를 위해, 목적함수의 수렴 조건을 판단하여 NSD의 수를 줄이고자 한다. 목적함수의 수렴 조건을 판단하기 위해 샘플 수를 NSO로 정의하며, 판단조건은 ϵ_r,o보다 작은 경우로 선정한다. 만약, 목적함수의 표준편차 값이 설정값(ϵ_r,o)보다 작은 경우 NSD=NSD-α로 변경하여 축차과정을 수행한다.

RDVM 위상최적설계를 위해서는 기존 위상최적설계 대비 4가지 파라미터가―NSD, NSO, ϵ_r,o 그리고 α― 요구된다.

3.1 위상최적설계 전처리 과정

이 연구에서는 RDVM 위상최적설계를 적용하여 자동차용 캘리퍼 개념 설계를 위한 수치해석을 진행하였다.

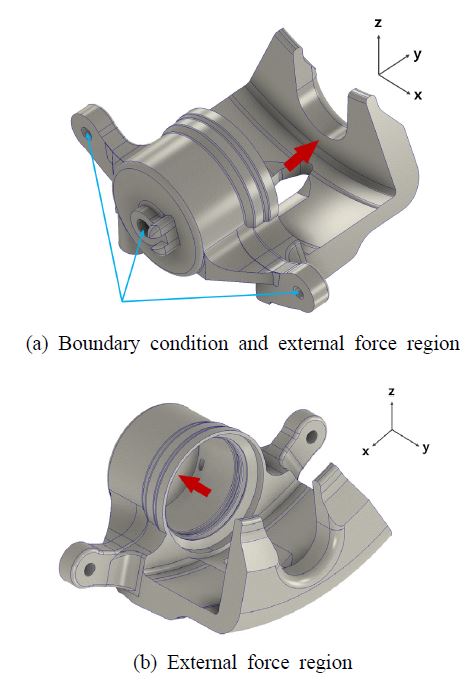
Fig. 1은 자동차용 캘리퍼의 형상을 나타낸 것이고, 화살표는 브레이크 역할을 위해 캘리퍼가 힘을 받는 방향을 나타낸 것이다. Fig. 1에서 붉은색 화살표는 힘의 방향과 위치를 나타낸 것이고, 하늘색 화살표는 캘리퍼의 고정점을 나타낸 것이다. Fig. 1 (a)에 나타낸 힘의 크기는 임의로 147.5 N, Fig. 1 (b)에 나타낸 힘의 크기는 17 N으로 선정하였다. 시뮬레이션을 위해서는 구조해석 전용 프로그램인 ANSYS 18.2를 사용하였으며, 최적설계 과정을 위해서는 in-house 코드를 사용하였다.

Fig. 1

A brake caliper shape with the external force directions and boundary conditions

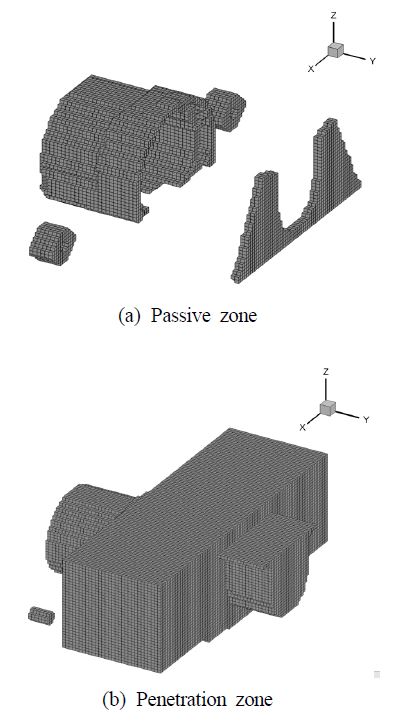
위상최적설계를 위해서는 설계영역 정의가 필요한데, 요소를 100(x-축방향) × 80(y-축방향) × 47(z-축방향)로 정의하여 총 376 000개의 설계인자를 생성하였다. 전체 설계영역의 크기와 물성치는 Table 1에 정리하였다. 요소는 노드 8개로 구성된 SOLID45를 사용하였다. 하지만, 설계영역에서도 캘리퍼 기능을 위해 반드시 물질이 존재하는 영역(passive zone)과 다른 부품과의 간섭 등으로 캘리퍼 설계영역에서 물질이 존재하지 말아야 하는 영역(penetration zone)을 정의하여야 한다. 반드시 물질이 존재하여야 하는 영역으로는 유압실린더 조립부, 나사고정부 및 디스크 패드 마찰부로 선정하였으며, 요소는 12 963개로 Fig. 2 (a)에 나타냈다. 존재하지 말아야 하는 영역으로는 타이어와 유압 실린더 간섭부위가 대부분이며, 볼트자리를 포함한 설계영역의 요소는 124 578개로 Fig. 2 (b)에 표시하였다. 그리하여 실제 설계인자 수는 238 459개이다.

Table 1

Material properties and design domain size for caliper topology optimization

Fig. 2

Preparation for topology optimization

또한, 기존 캘리퍼의 기준값을 정의하기 위해 기존 캘리퍼의 컴플라이언스를 계산하여 본 결과 575.3의 값으로 나왔으며, 설계영역 대비 체적은 약 15 %로 정의되었다. 그리하여 컴플라이언스 기준값은 575.3으로, 체적 제한조건은 15 %로 정의하였다.

3.2 기존 및 RDVM 위상최적설계 결과 비교

이 연구에서는 기존의 캘리퍼와 동일한 질량으로 가정하여 기존 및 RDVM 위상최적설계를 진행하여, 기존 캘리퍼와의 컴플라이언스 비교와 기존 및 RDVM 위상최저설계의 결과값을 비교하였다.

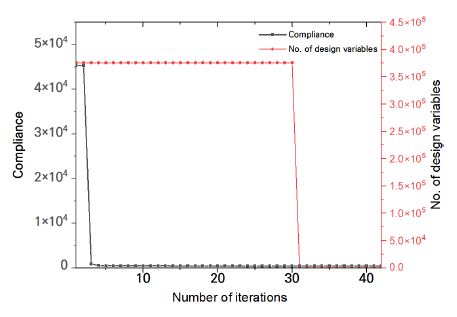
기존 위상최적설계기법을 적용한 컴플라이언스 및 체적비(volume ratio)를 축차별로 Fig. 3에 표시하였다. 여기서 체적비는 기존 캘리퍼의 체적으로 나눈 값으로 정규화시킨 값이다. 컴플라이언스 값은 축차 3번째부터 거의 수렴한 것으로 판단되나, 체적비는 30번째 축차이후 수렴을 한 것으로 판단된다. Fig. 3에서 알 수 있듯이, 축차 30번째 이후 컴플라이언스 및 체적비의 값의 변동은 거의 없다. 기존 위상최적설계를 적용하여 얻은 컴플라이언스 값은 Table 2에 나타냈으며, 기존 캘리퍼 보다 약 30 %의 성능향상이 되었음을 알 수 있었다. 기존 위상최적설계기법을 적용하여 얻은 캘리퍼의 형상은 RDVM 위상최적설계기법을 적용하여 얻은 결과(Fig. 4)와 거의 일치하였다.

Fig. 3

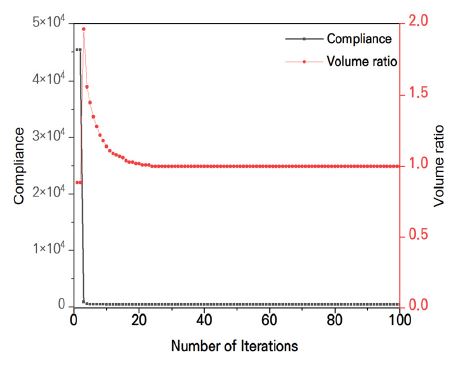
The history of optimal results for the objective function and volume ratio by conventional topology optimization

Table 2

RDVM parameters and summarized topology optimization results corresponding to Figure 4

Fig. 4

RDVM topology optimization result for caliper design with respect to different views

기존의 위상최적설계는 식 (3)의 수렴조건을 만족하기 위해서 100회의 축차가 요구되어지나, RDVM 위상최적설계의 경우는 동일한 결과를 얻는데 42회의 축차가 필요하여 시뮬레이션 시간을 58 %가량 절약할 수 있었다.

RDVM 위상최적설계 수행을 위해 NSD는 30으로 선정한 이유는 기존 위상최적설계의 데이터를 기반으로 30번째 축차이후 안정적으로 수렴되었기 때문이다. RDVM 위상최적설계 적용을 위해 필요로 하는 파라메터의 값들은 Table 2에 정리하였으며, 캘리퍼의 성능을 평가하는 컴플라이언스 값도 기존 위상최적설계의 결과와 거의 일치하는 것을 알 수 있었다.

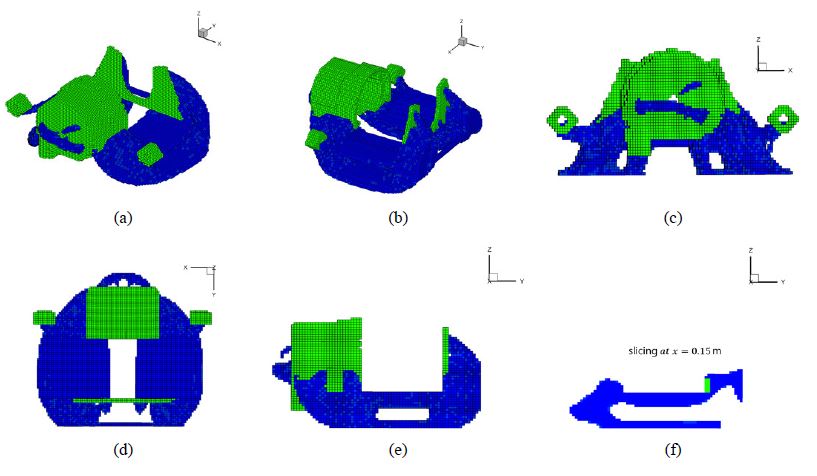
위상최적설계 기법을 적용하여 캘리퍼의 설계를 진행한 결과 기존의 캘리퍼 형상과는 차이가 있음을 알 수 있었다. Fig. 4는 RDVM 위상최적설계를 적용하여 얻은 결과에 대한 것을 다양한 각도와 방향에 따라 나타낸 것인데, 녹색으로 표현된 부분은 passive zone을 나타낸 것이고, 파란색으로 표현된 부분이 위상최적설계를 통해 얻은 결과물이다. 파란색부분은 설계변수가 0.9 이상의 값을 가진 요소만 표현한 것이다. 기존 캘리퍼와 형상의 관점에서 보면 2가지 큰 차이점이 있다. 궁극적으로 passive zone을 제외하면, 유압 실린더가 조립되는 부분과 패드와 마찰되는 부위를 연결하는 부분이 기존 캘리퍼와는 다름을 알 수 있었다. 하나는 기존 캘리퍼의 경우 연결부위가 top-view관점(Fig. 4 (d))에서 보면 가운데 집중되어 연결이 되어 있으나, 위상최적설계 기법을 적용한 결과는 가운데 부분은 비어둔 상태로 양쪽으로 재료가 집중되어 있음을 알 수 있다. 기존 캘리퍼는 양쪽 조립부위를 기준 내측으로 연결부위가 설계되어 있으나, 위상최적설계를 적용한 결과는 Fig. 4 (c)에서와 같이 양쪽 조립부위까지 연결부위가 넓게 분포되어 있으며, 가운데 부분은 비워진 것을 알 수 있다. 다른 하나는 side-view관점(Fig. 4 (e))에서 바닥면의 두께 방향으로 중간 부분이 비워진 것을 알 수 있다. 또한, Fig. 4 (f)는 x=0.15 m에서 YZ평면과 평행한 평면으로 slicing한 것이며, z방향에서 가운데 부분이 비워져 있음을 알 수 있었다. 위의 2가지가 기존의 캘리퍼와의 가장 큰 차이라고 할 수 있다.

RDVM 위상최적설계를 이용하여 얻은 컴플라이언스 및 설계변수 수의 변화를 축차수에 따른 변화를 Fig. 5에 나타내었다. 컴플라이언스의 변화는 기존 위상최적설계와 동일한 패턴을 유지하였으나, 설계변수(NDV) 수는 NSD 설정값인 30번째 이후로 급격히 줄어드는 것을 알 수 있었다. RDVM 위상최적설계기법을 통해 축차를 획기적으로 줄여 약 60 %의 시간절약 효과를 얻을 수 있었으며, 실제 문제인 자동차 캘리퍼의 성능도 기존 위상최적설계 결과와 거의 동일하게 기존 캘리퍼 대비 30 % 향상시킬 수 있었다.

Fig. 5

The history of optimal results for the objective function and volume ratio by the RDVM topology optimization