압전효과를 고려한 고속조종거울의 유한요소 해석 모델 구축
© The Korean Society for Noise and Vibration Engineering
Abstract
A laser weapon is a directed-energy weapon system that uses a high-energy laser to target and destroy the enemy. To precisely control laser to the target, the FSM (fast steering mirror) is an essential component in the precise control strategy. FSMs are optical devices that accurately aim a laser beam using the mirror's reflective surface and typically require large deflection and wide bandwidth. However, since a piezo-based actuator is utilized to drive the FSM, the dynamic characteristics of the actuators affect the overall system. In this study, static and dynamic performances were predicted by establishing a piezoelectric coupling analysis model of an FSM that amplified the piezo actuator. The performances in static and dynamic operation were subsequently calculated.
Keywords:
Large-scale Fast Steering Mirror, Tip-tilt Actuator, Finite Element Analysis키워드:
대구경 고속조종거울, 팁-틸트 구동장치, 유한요소 해석1. 서 론
레이저 무기는 지향성 에너지 무기(DEW, directed-energy weapon) 체계 중 하나로 고에너지의 레이저를 이용하여 미사일, 항공기 등 적 무기체계의 센서부 또는 동체 취약부에 조사하여 기능을 상실하게 하는 신개념 무기체계이다(1). 최근에는 드론 기술이 발달하면서 공격용 드론에 대응할 방공 무기 체계 중 하나로 레이저 무기에 대한 연구 개발이 활발히 이루어지고 있다(2).
레이저 무기의 상용화를 위해서는 레이저를 표적에 일정 시간 이상 집속시키는 기술이 필수적이다. 이를 위한 레이저의 추적 및 조준 체계는 넓은 범위의 제어인 거친 추적(coarse tracking)을 수행하는 김발 구동장치 제어부와 미세 범위를 추적하는 정밀 추적(fine tracking)을 통해 지향오차 및 외란을 제거하는 정밀 추적부로 나뉘어진다(3). 그중 정밀 추적을 담당하는 주요 구성품으로 고속조종거울(fast steering mirror, FSM)은 빔 경로 조종 및 빔 정렬 등을 수행한다.
고속조종거울은 거울의 반사면을 이용하여 레이저 빔을 빠르고 정확하게 조준하는 광학 메커니즘 기구로 정밀 추적을 위해 고속 응답, 대변위, 고정밀 등의 구동 성능이 요구된다. 이를 구현하기 위한 구동기로는 고해상도 및 선형성을 장점을 이용하는 VCA(voice coil actuator)(2~5)와 상대적으로 적은 변위에서의 고속 응답을 구현할 수 있는 PCSA(piezo ceramic stack actuator)(6,7)가 주로 적용된다.
그중 PZT 기반 액추에이터인 PCSA는 전체 길이의 약 0.1 % 수준의 적은 스트로크를 발생시키기 때문에 변위증폭기를 구조물을 활용하여 고속 응답의 장점을 유지하면서 상대적으로 큰 변위를 구현하고자 하는 APA(amplified piezoelectric actuator)를 이용한 고속 조준 거울이 개발되고 있다(8). 변위증폭기는 일반적으로 얇은 shell 구조물로 이루어져 있으며, 지렛대의 원리를 이용해 PCSA에 비해 더 큰 스트로크를 발생시킬 수 있다. 하지만 이러한 구조물은 구동기를 제외한 기존의 구성품에서는 예측할 수 없는 국부적인 공진과 같은 동특성이 발생하여 전체적인 시스템의 성능에 영향을 미치기 때문에 고속 조종 거울의 성능 확보에 있어서 이를 고려한 설계가 필수적이다.
이 연구에서는 APA를 적용한 고속조종거울의 목표 성능 확보를 위한 압전효과를 고려한 해석모델의 구축 방법을 제시하고자 한다. 압전형 구동기는 고속조종거울의 구조물 강성 및 변위에 따라 가변적인 추력 및 변위를 발생시키므로 압전형 구동기의 특성을 반영하는 성능을 예측하여 설계하는 것이 필수적이다. 이를 위해 변위증폭기가 적용된 압전형 구동기의 압전-구조 연성 해석 모델을 구축하고 이를 전체 시스템에 적용하여 해석하였다. 또한 연성 해석을 하지 않았을 때의 정적 및 동적 특성의 차이를 비교하기 위해 APA를 등가 스프링과 추력으로 치환한 구조와 비교 및 분석하였다.
2. 유한요소 해석
2.1 유한요소 해석 모델 구축
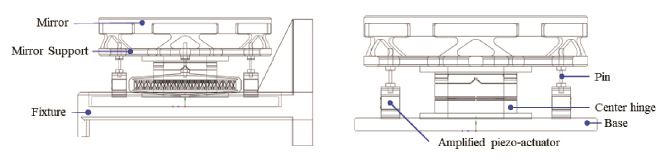
이 연구의 대상은 Fig. 1과 같이 Φ120 mm의 거울의 팁/틸트 각변위를 조정할 수 있는 소형 구조물이다. 고속 조종 거울의 구성은 레이저를 반사하는 거울 및 거울 지지부, tip/tilt 구동을 가능케 하는 중앙 가이드 구조물, 그리고 고속 조준 거울의 동력을 제공하는 구동부로 나뉜다. 거울 지지부는 3점 지지를 통해 운용 시 레이저에서 발생하는 내부 구조물로 열이 전달되는 것을 방지하고, 거울과 타 구조물을 연결하는 역할을 한다. 중앙 가이드 구조물은 탄성 힌지(flexure hinge) 구조를 적용하여 팁/틸트 방향에서의 강성은 낮고 이외의 강성을 높아 타 구동을 억제하도록 하는 상부 탄성 힌지와 단방향 구동만 가능한 피에조 액추에이터의 구동을 원활하게 해주는 하부 탄성 힌지로 이루어진다. 또한 팁틸트 구동을 위한 구동기는 변위증폭기의 역할을 하는 shell 형상이 포함된 4개의 APA로 이루어져 있다. 고속조종거울은 구동 시 4개의 구동기에서 직선 방향의 스트로크가 발생하고, 구동기 간의 상대 변위에 따라 거울의 레이저의 반사각을 조절하여 정밀 추적 및 빔 정렬을 가능케 한다.
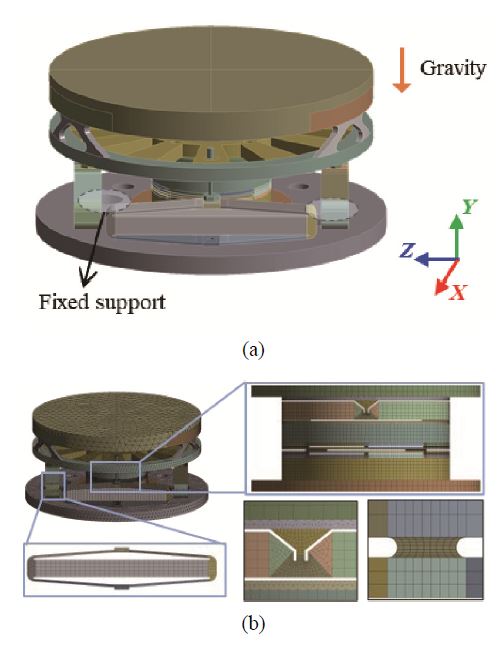
구동기의 성능 예측 위해 유한요소 해석 모델을 구축하였으며 작성된 해석 모델은 Fig. 2와 같다. 해석에 사용된 프로그램은 정적 및 동적 해석에 관련하여 기 검증된 전산 코드인 ANSYS Mechanical 2021R2 상용 프로그램을 사용하였다. 또한 piezoelectric-structural 연성 해석을 위하여 ACT extension을 이용하여 해석을 진행하였다. 유한요소 해석모델을 구축하는 데 있어서 전체적인 거동에 큰 영향을 미치지 않을 것으로 판단되는 필렛 등은 모 델링 과정에서 생략하였다. Fig. 2 (a)에는 해석에 적용된 경계조건 및 초기조건으로 베이스에서 고속조종거울을 고정하기 위해 사용되는 볼트는 중앙 가이드 구조물의 탄성 힌지의 강성보다 상대적으로 매우 높은 강성을 갖기 때문에 볼트가 체결되는 면에는 고정(fixed) 경계조건을 적용하였다.
최종적으로 구축된 유한요소 해석모델은 Fig. 2(b)와 같으며 수 mrad 수준에서 거동하는 탄성 영역에서의 선형 해석이 목적이기 때문에 각 방향으로 2개의 적분점을 사용하는 1차 요소(SOLID185)를 이용하였다. 중앙 가이드 구조물은 적용된 상부 및 하부 탄성 힌지 부위에 응력이 집중되기 때문에 상세 모델링을 진행하였으며 고속조종거울에 대한 유한요소 해석모델은 총 323 377개의 요소와 216 909개의 절점으로 이루어진다. 또한 piezoelectric-coupling 고려되지 않은 해석 모델과의 결과와 비교하기 위해 동일한 경계조건과 격자 구성을 갖고 APA 구조물을 등가 스프링으로 치환하고 구동기의 추력을 force로 적용한 해석모델을 추가로 작성하였다.
2.2 기전연성해석 모델 구축
기전연성해석을 통해 시스템 전체의 성능을 예측하기 위해서는 APA 단품에 대한 해석 모델에 대한 검증을 우선하여야 한다. 이 연구에서 사용된 구동기는 CEDRAT 사의 APA600MML 모델을 선정하였 고 이에 대한 규격은 Table 1에 나타나 있다.
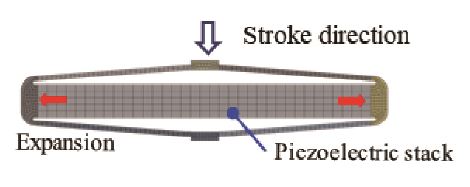
Fig. 3에는 변위증폭기가 적용된 APA600MML의 작동 원리를 보여준다. APA는 변위증폭기 역할을 하는 Shell 구조물이 PCSA에 부착되어 있으며, PCSA에 전압이 가해짐에 따라 역압전효과에 의해 PCSA가 축 방향으로 확장되어 단방향으로 줄어드는 방향으로 작동한다.
PCSA는 전압이 인가됨에 따라 압전 재료의 내부에 발생하는 응력이 발생하고, 응력에 따라 PCSA 내부에서 변형을 발생시키는 역압전효과에 의해 구동기로써 작동한다. 일반적으로 PCSA의 스트로크는 전체 길이의 약 0.1 % 수준으로 발생하고, 추력은 넓이에 비례하게 된다. 이때의 응력과 변형률의 관계는 식 (1)과 (2)에 따라 계산된다.
| (1) |
| (2) |
여기서 s는 변형률 텐서, T는 응력 텐서, E는 전계 텐서, D는 전기 변위 텐서이다. 그리고 압전재료의 물성 c, e, ε는 각각 일정한 전기장에서의 강성, 일정한 응력에서의 압전 응력 상수와 유전계수이다.
PCSA는 동일한 길이 내에서 높은 스트로크를 발생하기 위해 전체 길이 내에서 많은 피에조 스택으로 적층되는데, 계산의 효율성을 위해 해석 모델 내에서 PCSA는 orthotropic한 물성을 갖는 솔리드 모델로 간주될 수 있으며 식 (3), (4)와 같이 표현되는 등가 물성치를 적용함으로써 요소 수를 감소할 수 있다(10).
| (3) |
| (4) |
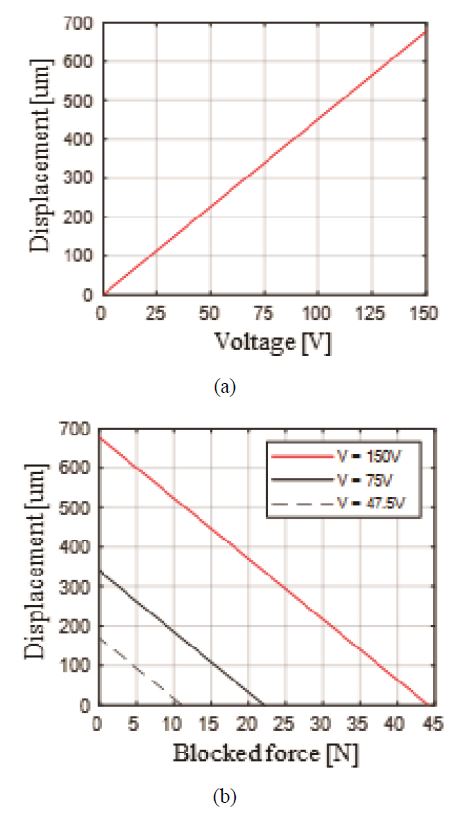
이때, d는 압전결합상수이고 n은 피에조 스택의 수이고 아래 첨자 3은 압전체의 polarization 방향이다. 또한 가용 가능한 PCSA의 추력과 변위는 전압에 관계 있다. PCSA에서 발생시킬 수 있는 최대 추력은 최대 전압에서 변위가 발생하지 않을 경우에 발생하는 차단력(blocked force)로 표현되고 PCSA에서 발생시킬 수 최대 변위는 최대 전압에서의 외력이 존재하지 않을 때인 자유 변위(free displacement)로 차단력과 자유 변위 사이의 관계는 Fig. 4와 같이 나타난다. Fig. 4(a)는 전압과 자유 변위와의 관계가 나타나 있는데, 인가 전압이 증가함에 따라 자유 변위가 증가됨을 보여준다. 반면 동일 전압에서도 PCSA가 발생시킬 수 있는 추력은 변위가 증가함에 따라 감소하게 되고 Fig. 4(b)에 나타나 있다. 대상 모델인 APA600MML의 단일 구동기에 대한 규격과 기전연성 해석 결과는 Table 1에 나타내었다. 연구에서 사용된 APA600MML의 차단력과 자유변위는 44.0 N과 78.0 ㎛로 이에 따른 액추에이터의 등가 스프링 강성은 65 N/mm이다. 기전연성 해석을 통해 단일 APA에서 해석한 결과는 차단력 44.15 N과 자유변위 675.0 ㎛, 정해석에서 낮은 수준의 오차로 기전연성해석의 모델을 검증할 수 있었다. 구동기의 동적 해석모델의 검증은 공진주파수를 기반으로 이루어졌고, 해석 모델과 규격과의 오차는 0.78 % 수준으로 대상 구동기의 기전연성 해석 모델의 동적 모델링도 낮은 오차로 모델링 되었음을 확인할 수 있다.
2.3 정적 해석 결과
이번 장에서는 앞서 작성한 APA600MML을 고속조종거울에 구동기로 적용한 기전연성해석 모델(Model 1)에서 정해석을 통해 제안된 고속조종거울의 최대 각변위를 예측하고 APA를 등가 스프링으로 치환한 등가 스프링 모델(Model 2)의 해석 결과와 비교하였다. 등가 스프링 해석 모델에서는 APA를 등가 스프링으로 치환하고 스프링 상수를 Table 1에 표기된 65 N/mm을 적용하여 해석하였다.
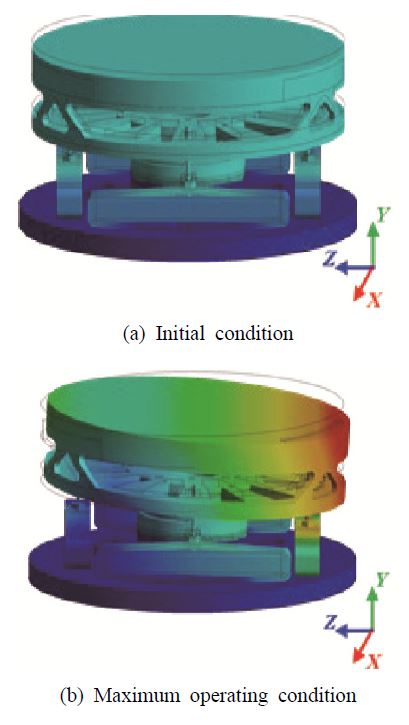
정해석의 과정은 다음과 같다. 이전 장에서 설명한 것과 같이 APA는 단방향의 변위만 발생시키기 때문에 고속조종거울은 최대 전압의 150 V의 50 %인 75 V를 4축의 모든 APA에 인가하였을 때를 기준으로 팁/틸트 구동을 하도록 설계되었고 모든 구동기에 초기 전압인 75 V가 인가된 상태를 초기 해석 조건으로 선정하였고, 이때의 구동 형상은 Fig. 5(a)와 같다.
이후 팁/틸트 거동을 위해 초기 조건에서 회전축을 기준으로 반대 방향의 2개의 APA에 서로 반대 부호의 추가 전압을 인가하여 팁/틸트 거동을 발생시키게 되며 이때, 구동기의 상대 변위에 의해 Fig. 5(b)와 같이 회전 축으로 거울이 회전한다. 정해석에서는 초기 전압을 기준으로 최대 작동 전압인 ± 75 V가 APA에 인가하였다. 반면, 등가 스프링 모델에서는 연성해석이 적용되지 않기 때문에 44.0 N의 50 %인 22.0 N을 초기 조건으로 설정하였고 회전축을 기준으로 반대 방향의 2개의 pin에 ± 22.0 N이 인가되어 고속조종거울에서 발생할 수 있는 최대 각변위를 도출하였고 해석 결과는 Table 2에 나타내었다.
해석 결과는 거울 중심부의 초기 조건에서의 거울 중심부의 Y 축 방향 이동 거리 yc와 최대 전압에서의 거울의 최대 각변위 θmirror, 그리고 회전 방향을 기준으로 서로 마주보는 APA의 스트로크를 비교하였다. 거울의 각변위 θmirror는 거울 고정부에 의해 응력을 받지 않기 때문에 거울은 강체로 가정하여 거울 중심의 Y축 방향 이동 거리 yc와 거울의 회전축 기준의 거울 가장자리의 Y축 방향 이동 거리 y1를 이용하여 식 (5)의 기하학적인 관계를 통해 계산하였다.
| (5) |
정해석 결과 고속조준거울에서 최대 구동 전압 ±75 V를 인가하였을 때 각변위는 6.83 mrad으로 계산되었다. 반면, 스프링으로 APA를 치환한 Model 2 에서 계산한 거울의 최대 각변위는 7.03 mrad으로 해석을 통해 FSM의 성능을 예측할 시 기전연성해석 모델인 Model 1에 비해 등가 스프링 치환 모델인 Model 2에서 비보수적인 결과를 도출한다는 것을 확인하였다. 이는 APA 구조물이 해석 모델로 반영되었을 때 팁/틸트 구동 시 전체 시스템의 회전 방향의 강성은 Model 1에서 더 높은 것으로 계산된다는 것을 판단할 수 있다.
반면 회전 방향 기준의 반대 방향의 두 액추에이터의 Stroke를 비교해보면, Y축 방향 이동 거리 y_c를 기준으로 Model 1보다 Model 2에서 더 큰 스트로크를 발생하는데 이는 적용된 등가 스프링 강성은 65.0 N/mm로 APA600MML의 강성 65.1 N/mm보다 낮지만 Shell 구조물로 인해 스트로크 축 이외의 강성이 반영되기 때문에 등가 스프링 치환 모델을 적용하는 경우 고속조종거울 구조물에서는 강성이 더 낮게 계산되는 것으로 분석할 수 있다.
2.4 동적 해석 결과
이번 장에서는 고속조종거울의 모드 해석을 기반으로 시스템의 동특성을 파악하였고 조화응답해석을 기반으로 open-loop에서의 시스템 구동대역폭을 예측하고자 한다. 조화응답해석은 모드 중첩을 기반으로 수행하였기 때문에 모드 해석을 사전에 수행하여 전체 구조물의 동특성을 분석하고 구동기에서의 외력에 따른 거울에서의 응답을 주파수 응답 함수로 계산하였다. 중력과 이전 장에서 설명했던 초기조건에서 pre-stressed 상태를 기반으로 동해석을 진행하였다.
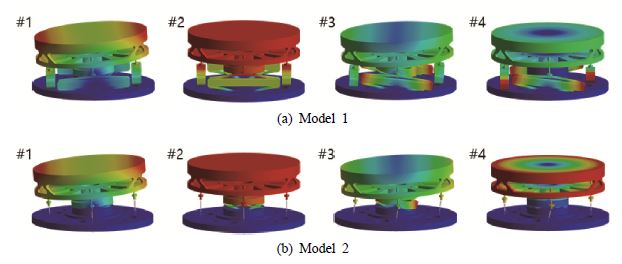
모드 해석을 기반한 조화응답 해석을 위해서는 관심 주파수 대역을 포함하여 고유진동수가 충분히 확보되도록 추출되어야 한다. 또한 구동대역폭은 주요 모드 이후의 부공진 모드에 의해 제한되기 때문에 팁/틸트 거동에 관련된 모드 이후 3개의 모드를 추출하였다. 이와 같은 기준을 기반으로 목표 bandwidth의 2배인 200 Hz 부근의 4개의 모드를 추출하였고 그 결과는 Fig. 6과 Table 3에 나타내었다. Fig. 6(a)은 조화응답 해석 시 기전연성 해석을 적용한 위해 APA의 구조물이 포함된 Model 1의 1차 ~ 4차 모드 형상이고, Fig. 6(b)는 APA를 등가 스프링으로 치환한 Model 2의 1차 ~ 4차 모드 형상이다.
해석 결과 제안된 고속조종거울에서 발생하는 주요 팁/틸트 거동에 관련된 모드는 1차에서 발생한다. 이때, 해석 모델에 따른 공진주파수는 Model 1에서 90.5 Hz와 Model 2에서 92.3 Hz에서 발생하여 APA가 등가 스프링으로 치환된 모델에서 더 높은 주파수에서 공진이 발생한다. 또한, 구동대역폭에 큰 영향을 미치는 이후의 저차 공진은 2차 모드에서는 하부 탄성 힌지에 의한 병진 운동, 3차 모드에서는 상부 탄성 힌지와 하부 탄성힌지에 의한 부공진, 그리고 4차 모드에서는 거울의 원주 방향으로 회전으로 인한 부공진이 발생한다.
앞서 정해석의 결과와 비교해볼 때, 동해석에서 구동기의 관성질량의 효과가 적용되지 않는 Model 2에서는 전체 시스템에서의 공진주파수가 높게 계산되어 구동대역폭을 기준으로 Model 1에 비해 비보수적으로 판단하게 됨을 확인할 수 있다.
다음으로는 조화응답 해석을 통해 고속조종거울의 운용 시 open-loop를 모사하여 주파수 응답 특성을 알아보고자 한다. 고속조종거울의 경우 팁/틸트 방향 2축의 회전을 목적으로 하는 구조물이기 때문에 회전축을 기준으로 2개의 구동기를 반대 부호로 전압을 인가하여도 충분한 자유도를 확보할 수 있지만, 이 때 발생하는 거울 중심부의 Y 축 방향의 이동을 제한하거나 PCSA를 이용하는 경우 압전소자의 비선형적인 특성을 보안하기위해 4개의 자유도를 이용할 수 있기 때문에 조화응답 함수의 해석 조건은 다음 두 가지 상황을 가정하여 해석을 진행하였다.
- 1) 4개의 APA를 각각 제어하는 경우
- 2) 4개의 APA를 회전축 기준으로 2개를 동시에 제어하는 경우
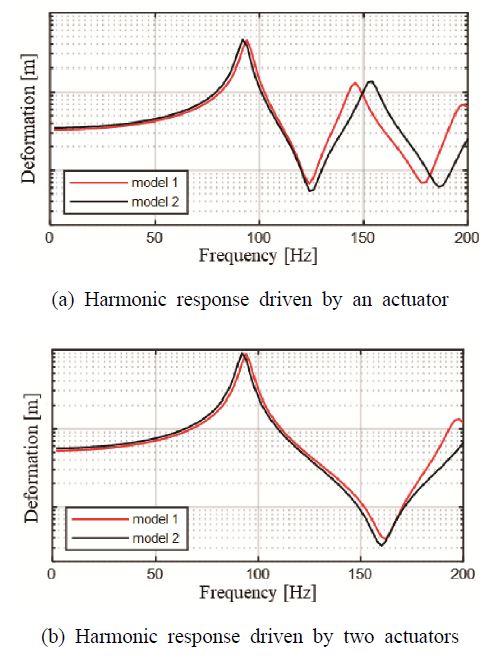
조화응답 해석을 통해 계산한 주파수 응답 함수의 계산 결과는 Fig. 7에 나타내었다. Fig. 7(a)는 1개의 구동기를 이용하였을 때 거울 가장자리의 Y 축 방향 변위를 계산한 결과를 Model 1과 Model 2를 함께 표시하여 비교하였다. Fig. 7(b)는 회전축을 기준으로 2개의 구동기로 고속조종거울을 제어할 때 거울 표면의 변위를 계산한 결과이다.
우선 Fig. 7(a)와 Fig. 7(b)를 비교해 보면, 고속조종거울의 제어 방식에 따라 부공진에 발생 여부를 확인할 수 있다. 각각의 APA를 제어하는 경우에는 140 Hz 부근에서 추가적인 공진이 발생하며 이는 Fig. 6(a)의 하부 탄성 힌지에 의한 거울의 병진 운동이 발생하는 2차 모드가 발현된다. 반면 회전축을 기준으로 2개의 구동기를 동시에 제어하여 팁/틸트 구동을 하는 경우, 2차 모드가 발현되지 않아 제어 관점에서 더 넓은 구동대역폭을 확보할 수 있음을 예측할 수 있다.
해석 모델에 따른 조화응답 해석 결과를 비교해보면, 1차 공진에서는 두 해석 모델에서의 공진점이 유사한 주파수에서 발생하나, 2차 공진 이후 부공진 발생 주파수가 Model 1에 비해 Model 2에서 더 높게 발생하게 된다. 각각의 구동기를 이용하여 제어할 경우 Model 1에서의 부공진은 146 Hz에서 발생하고Model 2의 경우 154 Hz에서 부공진이 발생하게 되며 이는 3차 모드가 제어 시 부공진에 영향을 미치는 것을 확인해 볼 수 있다. 따라서 이를 기준으로 구동 주파수 대역을 예측하였을 경우 APA를 기전연성 해석하는 경우 스프링으로 치환한 Model 2보다 실제 시스템을 더 보수적으로 예측할 수 있다.
3. 결 론
이 연구는 압전형 구동기를 적용한 고속조종거울의 성능을 예측하기 위하여 수행되었다. 변위증폭기가 포함된 압전형 고속조종거울의 경우 구동기의 동특성이 전체 시스템의 동특성에 영향을 미칠 수 있기 때문에 압전 특성을 반영한 유한요소 해석모델을 구축하는 방법론에 대해 기술하였다. 기전연성 해석 모델은 제조사의 성능표와 해석 결과를 비교하여 검증하였으며, 그 오차는 정적 해석에서 최대 0.44 %와 동적 해석에서 0.78 % 수준으로 해석모델이 작성되었다. 이를 기반으로 구동기를 등가 스프링으로 치환한 해석 모델의 해석 결과를 비교하여 등가 스프링 모델을 통해 구조물을 분석할 때 발생할 수 있는 오차에 대해 제시하였다. 이 연구에서 제시하는 연성해석 방법을 통해 압전형 구동기가 포함된 구조물의 성능을 예측할 때 더 신뢰성 있는 해석 방법론을 제공할 수 있을 것으로 기대한다.
기 호 설 명
| c : | Elastic stiffness at constant electric field |
| D : | Electric displacement tensor |
| d : | Piezoelectric coupling coefficient |
| E : | Electrical field tensor |
| e : | Piezoelectric stress at constant strain |
| n : | Number of piezo layers |
| rmirror : | Radius of mirror |
| s : | Strain tensor |
| T : | Stress tensor |
| y : | Displacement in Y direction |
| ϵ : | Dielectric coefficient at constant strain |
| θmirror : | Angular displacement |
Acknowledgments
이 연구는 LIG NEX1 산학협력과제 지원으로 수행되었습니다.
References
- Lee, S. H., Kwak, D. H. and Jeong, E. B., 2021, A Study on the Fast Steering Mirror for Laser Weapon System, Proceedings of KSPE 2021 Spring Conference, Vol. 21, No. 5, pp. 644~645.
-
Yoo, J. S., Lim, S. B., Jung, J. W., Jung, S. W., Kim, J. H., Yoon, J. Y., Lee, S. H., Kwak, D. H., Jeong, E. B. and Park, N. C., 2021, A Study for Reliability Verification of Structural Design of Fast Steering Mirror with Voice Coil Actuators, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 4, pp. 442~449.
[https://doi.org/10.5050/KSNVE.2021.31.4.442]

-
Ulich, B. L., 1988, Overview of Acquisition, Tracking, and Pointing System Technologies, Acquisition, Tracking, and Pointing II, Vol. 887, pp. 40~63.
[https://doi.org/10.1117/12.944208]

-
Kluk, D. J., Boulet, M. T. and Trumper, D. L., 2012, A High-bandwidth, High-precision, Two-axis Steering Mirror with Moving Iron Actuator, Mechatronics, Vol. 22, No. 3, pp. 257~270.
[https://doi.org/10.1016/j.mechatronics.2012.01.008]

-
Kim, K. H., Oh, D. H., Shin, B. H. and Lee, S. Y., 2009, A HDD Latch Design using Electro-magnetic Force of VCM Actuators, Transaction of the Korean Society for Noise and Vibration Engineering, Vol. 19, No. 8, pp. 788~794.
[https://doi.org/10.5050/KSNVN.2009.19.8.788]

-
Zhu, W., Bian, L., An, Y., Chen, G. and Rui, X., 2015, Modeling and Control of a Two-axis Fast Steering Mirror with Piezoelectric Stack Actuators for Laser Beam Tracking, Smart Materials and Structures, Vol. 24, No. 7, 075014.
[https://doi.org/10.1088/0964-1726/24/7/075014]

-
Shao, S., Tian, Z., Song, S. and Xu, M., 2018, Two-degrees-of-freedom Piezo-driven Fast Steering Mirror with Cross-axis Decoupling Capability, Review of Scientific Instruments, Vol. 89, No. 5, 055003.
[https://doi.org/10.1063/1.5001966]

-
Wan, Y., Xiong, H., Song, T., Zhou, G., Huang, M., Liu, J., Hou, X. and Chen, W., 2022, Design of a Fast Steering Mirror Driven by Piezoelectric Ceramics, Optical Engineering, Vol. 62, No. 2, 024102.
[https://doi.org/10.1117/1.OE.61.2.024102]

- Kenneth, G. M., 1995, Vibration Testing: Theory and Practice, John Wiley & Sons, New York, NY.
-
Zhang, Y. and Lu, T. F., 2019, On an Equivalent Model of Multi-layer Piezoelectric Actuators for Facilitating Finite Element Simulations, Microsystem Technologies, Vol. 25, No. 12, pp. 4455~4464.
[https://doi.org/10.1007/s00542-019-04464-6]


Seonbin Lim is graduate school student in mechanical engineering at Yonsei University and currently majoring in Structural Vibration. He is especially interested in vibration transmissions in electric vehicles.

No-Cheol Park received B.S., M.S. and Ph.D. degrees from Yonsei University in 1986, 1988, and 1997, respectively. Dr. Park is currently a professor at department of Mechanical Engineering in Yonsei University.