[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 1, pp.5-15

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Feb 2023

Received 06 Jul 2022 Revised 30 Aug 2022 Accepted 09 Jan 2023

DOI: https://doi.org/10.5050/KSNVE.2023.33.1.005

수중 무기 추진체의 진동 충격 환경조건에 대한 구조 안전성 분석

이창민^† ; 최재엽^* ; 박정훈^* ; 전관수^*

Structural Safety Analysis for Vibration and Shock Environmental Conditions of Underwater Weapon Propellant

Chang Min Lee^† ; Jae Yeop Choi^* ; Jung Hun Park^* ; Gwan Su Jeon^*

*LIG Nex1, Researcher

Correspondence to: ^†Member, LIG Nex1, Researcher E-mail : changmin.lee@lignex1.com # A part of this paper was presented at the KSNVE 2021 Annual Autumn Conference‡ Recommended by Editor Pyung Sik Ma

Abstract

Navy ships are exposed to vibrations and shocks during operations in various underwater environments. Underwater weapons, such as torpedoes and mines mounted on ships, transmit vibrations and shocks directly to the ships. Underwater weapons must be designed safely to avoid an explosion in the self-ship caused by transmitted vibration and shock. In this study, structural safety was investigated in relation to vibration and shock environmental conditions for an underwater weapon propellant. Vibration analyses in accordance with the Mil-E-82590 standard were performed to evaluate fatigue durability. Shock analyses of the deck launch condition were performed in accordance with the Mil-T-18404 standard. Furthermore, the structural safety was analyzed by performing an underwater explosion analysis based on DDAM. Finally, the concept of PVSS was introduced, and the analysis method of shock events was explained.

Keywords:

DDAM, Integrated Motor Propulsor, PVSS(Pseudo Velocity Shock Spectrum), Shock, Underwater Weapon Propellant, Vibration

키워드:

동적설계해석법, 일체형 추진장치, 충격, 수중 무기 추진체, 진동

1. 서 론

해군의 함정은 운용 중 다양한 수중 환경에서 진동, 충격에 노출된다. 함정에 탑재되는 어뢰 및 기뢰 등의 수중 무기 또한 함정에 작용하는 진동과 충격이 그대로 전달된다. 수중 무기가 구조적으로 안전하게 설계되지 않은 경우 함정에서 전달되는 진동, 충격에 의해 자함에서의 폭발 가능성을 배제할 수 없다. 수중 무기, 특히 어뢰의 경우 외부 환경 외에도 입수충격을 고려하여야 한다. 입수충격에 의해 자함 근처에서 폭발하는 경우도 상당한 위험요소이기 때문이다. 따라서 수중 무기의 구조 안전성 설계는 매우 중요한 요소이다. 국내에서 개발하는 수중 무기에 적용되는 환경 규격은 진동/충격 규격 모두 MIL-T-18404⁽¹⁾ 절차를 따르거나 진동 규격은 MIL-E-82590⁽²⁾ 충격 규격은 MIL-T-18404를 따르는 경우가 있다.

이 논문의 경우는 무기 요구사항에 의해 후자의 경우로 분석을 진행하였다. 진동은 함정 운행 중의 진동으로 규정하며, 충격은 Fig. 1과 같이 어뢰 발사 위치 및 발사 방식에 따라 구분한다. 중어뢰의 경우 침수관 발사대를 통해 수중에서 발사하여 진행되므로 입수충격을 받지 않는다. 경어뢰의 경우 갑판에서 발사하여 입수 후 진행하여 약한 충격이 작용한다. 홍상어 등은 공중으로 발사하여 입수 후 진행하게 되며, 가장 강한 충격이 작용한다. Moon 등⁽³⁾은 수중폭발실험으로부터 계측한 최대 압력신호에 대한 유효성 확인, 검증 및 인정 과정을 적용하는 방안을 제안하였다. Kim⁽⁴⁾은 항공기나 헬기에서 투하되어 수면으로 입수하는 경어뢰 입수 충격력을 근사적으로 추정할 수 있는 방법을 제시하였다. Kim 등⁽⁵⁾은 고속으로 입수하는 물체에 대해 탄두 형상과 입수각도에 따른 충격량 및 입수 거동을 해석하였다. 하지만 수중 무기의 진동, 충격 환경조건에 대한 전반적인 해석 절차를 언급한 사례는 없다.

Fig. 1

Type of torpedo launching methods

이 논문에서는 MIL-E-82590 규격의 진동 환경조건과 MIL-T-18404 규격의 입수충격, MIL-S-901D⁽⁶⁾ 규격의 수중폭발을 모두 고려하여 구조 안전성을 분석하였다. 또한 입수충격의 경우 PVSS(pseudo velocity shock spectrum) 개념을 도입하여 모달 속도를 통해 안전성을 분석할 수 있는 또 다른 방법을 제안하였다.

2. 본 론

2.1 분석 대상 범위 및 해석 프로세스

(1) 분석 대상 범위

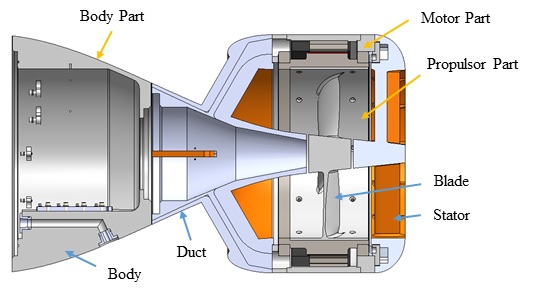
이 논문의 대상 장비는 Fig. 2와 같이 수중 무기의 추진력을 제공하는 일체형 추진장치이다. 일체형 추진장치란 기존 축계 시스템을 제거하여 추진기와 추진전동기가 일체형으로 제작되는 추진장치이다. 일체형 추진장치는 크게 몸체부, 추진전동기부, 추진기부로 구성된다. 기능품의 경우 장비의 on/off 모사 및 전자 소자들에 대한 해석 결과의 판단이 불가하여 기능품이 많은 추진전동기부를 제외한 몸체부와 추진기부의 구조물에 국한해서 해석 결과를 분석하였다. 전체 중량을 유지하기 위해 추진전동기부의 기능품 위치에 점질량을 인가하였으며, 해석을 위한 최소한의 형상을 유지하였다.

Fig. 2

Schematic of propellant

(2) 해석 프로세스

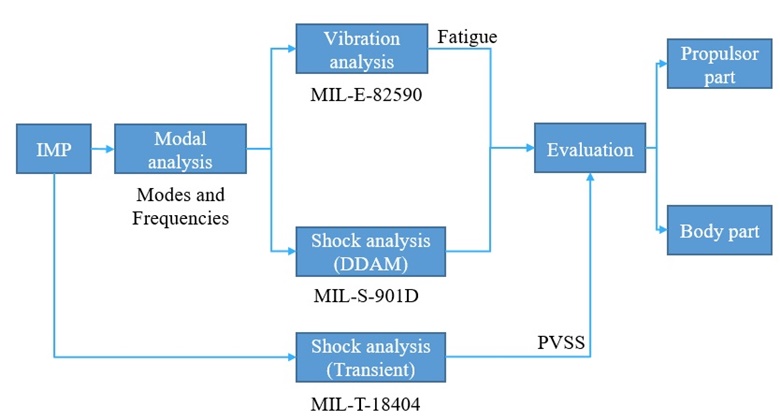
이 논문의 해석 프로세스는 Fig. 3과 같다. 고유모드 해석 후 강제진동해석과 피로해석을 통해 진동에서의 구조 안전성을 평가하였고, MIL-S-901D의 수중폭발해석은 과도응답해석으로 평가하였다. 또한 미해군 표준해석방법으로 지정된 DDAM(dynamic design analysis method) 절차에 의해 내충격 설계를 추가로 검증하였다. 입수충격의 경우 MIL-T-18404 중 갑판에서 발사하여 입사하는 경어뢰에 대해 과도응답해석을 수행하였고, PVSS를 통해 구조 안전성을 추가 분석하였다.

Fig. 3

Process of analysis

(3) 해석에 적용되는 시험 규격

- 진동해석

MIL-E-82590의 진동시험 규격은 두 가지 방법으로 규정한다. 첫째로 Table 1의 각 주파수 구간 별로 3 ~ 5분 동안 연속적으로 주파수가 변하도록 시험하는 방법이다. 둘째로 각 주파수 구간을 5 Hz 간격 이하로 동등하게 나누어 단일 주파수로 시험하는 방법이다. 이 논문에서는 두 번째 방법을 채택하여 1 Hz 간격으로 강제진동해석의 입력값으로 사용하였다.

Table 1

Schedule of vibration test

- 충격해석(DDAM)

DDAM은 과거의 전체 선박 충격 시험 및 대규모 모델 시험에서 도출된 충격 스펙트럼 설계 가속도 및 속도 계수를 통해 수상함과 잠수함의 다양한 장착 위치에 대한 충격 설계 값을 정의한다. 해석에 필요한 충격 설계 값(D_a)을 얻기 위한 절차는 다음과 같다.

1) 함 유형/설치위치/충격 응답 방향(vertical, athwartship, fore and aft)/탄성 또는 탄소성 선택을 통한 계수 결정한다.

2) 고유진동수 해석을 통해 식 (1), (2)에서 모달 중량(kips)을 계산한다.

W a = g ∑ i M i X ¯ i a 2 ∑ i M i X ¯ i a X ¯ i a 2 l b s

(1)

W a ¯ = W a 1000 k i p s

(2)

여기서, W_a, g, M_i, X_ia 는 각각 모달중량 행렬, 중력가속도, 질량 행렬, 변위 행렬이다.

3) 모달 중량을 이용하여 식 (3), (4)에서 A₀, V₀ 값을 계산한다.

A 0 = A a A b + W ¯ a A c + W ¯ a A d + W ¯ a 2 i f A d ≠ 0 A a A b + W ¯ a A c + W ¯ a i f A d = 0

(3)

V 0 = V a V b + W ¯ a V c + W ¯ a

(4)

4) A₀, V₀값과 1)에 의해 결정된 계수 A_f, V_f를 이용하여 식(5), (6)을 이용하여 A_a, V_a를 계산한다.

A a = A f A 0

(5)

V a = V f V 0

(6)

여기서, A_a, A_b, A_c, A_d는 가속도 계수이며, V_a, V_b, V_c는 속도 계수이다. A_f와 V_f는 탄성과 탄소성 재료에 따른 가속도와 속도 계수이다.

5) A_a에는 중력가속도 g를 곱하고, V_a에는 ω_j를 곱한다.

6) 위 두 값들 중 작은 값을 D_a로 결정. 만일 두 값 중 작은 값이 6 g보다 작을 경우 D_a = 6 g로 결정한다. 함 유형과 설치 위치, 충격 방향 및 탄성 여부에 따른 계수는 Tables 2 ~ 3과 같다⁽⁷⁾.

Table 2

Coefficients of shock design for submarines

Table 3

Coefficients of shock design for surface ship

- 충격해석(과도응답해석)

MIL-T-18404의 충격시험 규격은 발사 위치 및 방식에 따라 다음 3가지 경우로 분류된다.

1) 데크 발사 후 수중 입수로 전환 :

크기 60 g ± 6 g, 지속시간 8 ms 이상의 반정현파

2) 외부 부착물 부착 후 공기 중 발사 후 입수 :

크기 150 g ± 15 g, 지속시간 8 ms 이상의 반정현파

3) 외부 부착물 없이 공기 중 발사 후 입수 :

크기 250 g ± 25 g, 지속시간 8 ms 이상의 반정현파

이 논문에서는 일반적인 어뢰의 기준인 1) 항의 데크 발사 후 수중 입수로 전환하는 경우에 대해 과도응답 해석을 수행하였다.

2.2 해석 결과

(1) 해석 모델링 및 경계조건

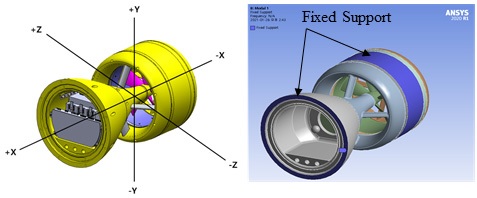
일체형 추진장치의 해석 대상 구성품은 알루미늄 재질로 제작된다. Table 4는 해석에 이용된 알루미늄의 물성값이다. 해석 대상에서 제외되는 기능품은 점질량으로 중량을 인가하였다. 해석을 위한 축 정의와 해석의 경계조건은 Fig. 4와 같다. 진행 방향을 X축으로 정의하고 그 외의 수직 방향을 각각 Y, Z축으로 정의하였다. 해석 경계조건은 타 어뢰체계의 진동/충격 시험조건과 유사하게 치구에 의해 고정될 예상 위치에 fixed support 조건을 인가하였다. 해석은 상용 해석 프로그램인 ansys 21.1을 활용하였다.

Table 4

Material properties of Al6061-T6

Fig. 4

Axis definition and boundary condition

(2) 모드해석

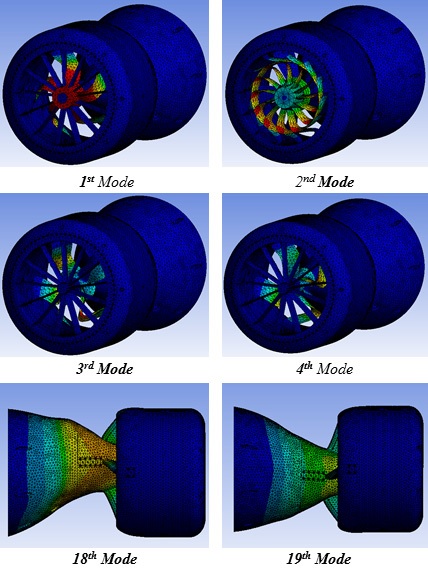
진동해석과 DDAM 해석을 위해 일체형 추진장치의 모드해석을 수행하였다. 모드해석 결과는 Table 5 및 Fig. 5와 같다. 1차 모드는 215 Hz로 추진기부에서 발생하며, 진동해석 범위인 10 Hz ~ 100 Hz 사이에 구조 공진이 없는 것을 알 수 있다. 7차 모드부터 16차 모드는 추진기부의 스테이터에서 국부적으로 발생하며, 18차와 19차 모드에서 몸체의 상하 및 좌우 모드가 발생한다.

Table 5

Result of modal analysis

Fig. 5

Mode shapes

(3) 진동해석

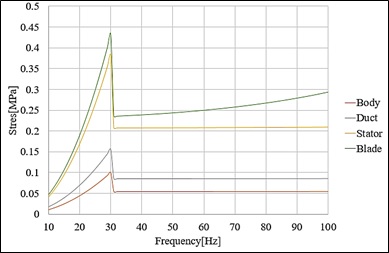
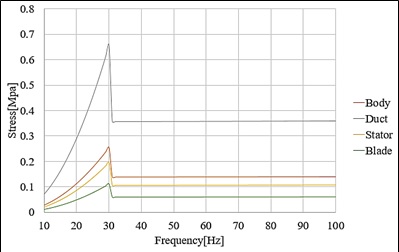
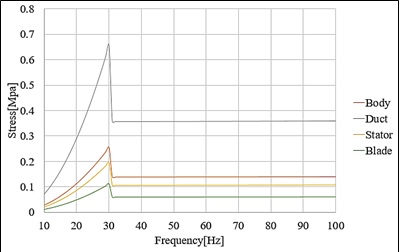
진동해석은 앞서 정의된 X, Y, Z 각 축 방향으로 Table 1의 주파수 구간을 1 Hz 간격으로 분할하여 가속도를 인가하였다. Figs. 6 ~ 8은 각 축 별 진동해석 등가응력 결과이다. X축과 Z축은 덕트조립체, Y축은 블레이드에서 가장 큰 응력이 발생하였다. ASTM B247M-02a⁽⁸⁾ 규격에 의하면 Al6061-T6의 허용응력은 240 MPa로 진동해석 결과 가장 큰 응력 0.8 MPa을 고려할 때, 안전율 300으로 구조적으로 매우 안전하다. 하지만 진동해석 시 입력 값에는 시간 지속의 개념이 없기 때문에 진동해석의 응력 결과만으로 구조 안전성을 고려할 수 없다. 따라서 피로해석을 통해 수명 관점의 구조 안전성을 분석하였다.

Fig. 6

Result of vibration analysis : X-axis

Fig. 7

Result of vibration analysis : Y-axis

Fig. 8

Result of vibration analysis : Z-axis

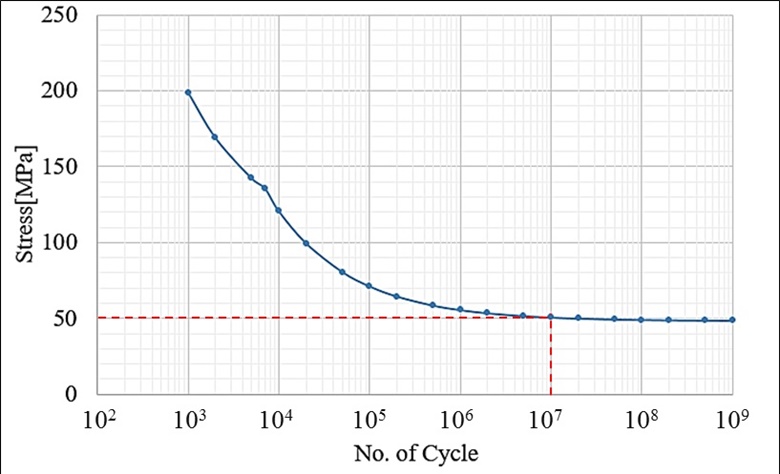
피로해석을 위해서는 Fig. 9와 같이 재료의 S-N 곡선이 필요하다⁽⁹⁾. 통상적으로 무한 수명은 10⁷ 사이클에서의 응력으로 평가한다. Al6061-T6의 경우 10⁷ 사이클에서 50.55 MPa 이하의 응력이 발생하면 무한 수명으로 간주할 수 있다. 해석 주파수 내에 구조 공진주파수가 없기 때문에 응력이 가장 높은 30 Hz와 주파수가 가장 높은 100 Hz에서 피로해석을 수행하였다. 시험규격에는 내구성에 대한 규정이 없으므로 이 논문에서는 30 Hz와 100 Hz 단일 주파수에서 전체 진동시험인 3시간을 적용하였다. Figs. 10 ~ 11은 피로해석 결과이다. 30 Hz와 100 Hz 모두 10⁷ 이상의 사이클로 무한수명으로 간주할 수 있으며, 이때의 안전율은 모두 15 이상인 것을 알 수 있다. 따라서 진동해석 결과 구조적으로 안전한 설계가 되었다.

Fig. 9

S-N curve of Al6061-T6

Fig. 10

Results of fatigue analysis ; 30 Hz

Fig. 11

Results of fatigue analysis ; 100 Hz

(4) 충격해석(DDAM)

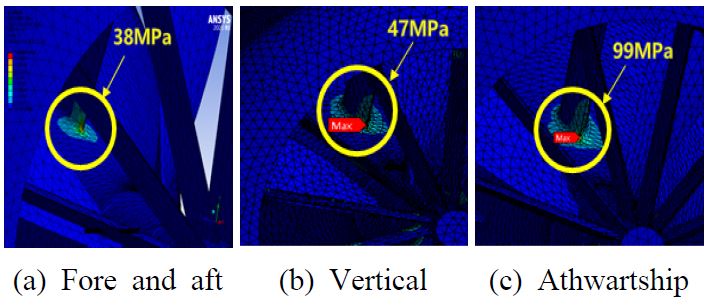
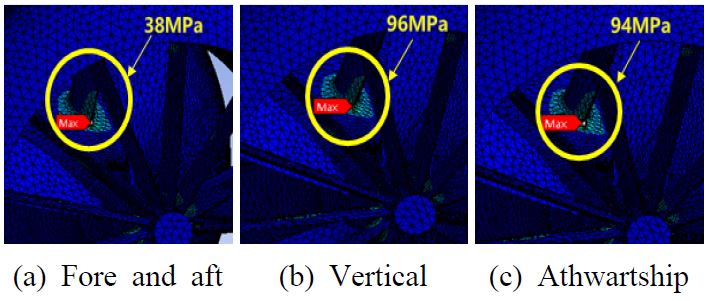
앞서 언급한 바와 같이 DDAM은 함정 탐재장비의 내충격성능을 검증하는 충격해석방법으로⁽¹⁰⁾ 장비의 중량 및 크기 제한조건으로 충격시험이 불가능한 탑재장비인 경우 사용된다. 일체형 추진장치는 충격시험이 가능한 조건이나 시험이 이루어지지 않아 DDAM을 통해 추가로 내충격 설계를 검증하였다. 일체형 추진장치는 상위체계가 미정인 장치로 함 유형, 설치 위치 및 충격 방향을 결정할 수 없다. 따라서 이 논문에서는 구조적으로 가장 취약할 수 있는 계수가 큰 경우를 선정하여 발생하는 장치에 작용하는 응력을 분석하였다. Tables 2 ~ 3의 계수에서 잠수함의 deck과 hull이 가장 큰 값임을 확인할 수 있다. Figs. 12 ~ 13은 해석 결과이다. 최대 응력이 발생하는 위치는 몸체와 덕트를 연결하는 스트럿 부위로 내부 케이블 경로의 역할을 하여 두께가 가장 얇은 취약부위이다. 해당 위치에서 38 MPa ~ 99 MPa의 등가응력이 발생하였으며, 알루미늄 허용응력 240 MPa 대비 안전율 2.5 ~ 6.3으로 구조적으로 안전한 설계가 되었다.

Fig. 12

Results of DDAM analysis ; submarine, deck condition

Fig. 13

Results of DDAM analysis ; submarine hull condition

(5) 충격해석(과도응답해석)

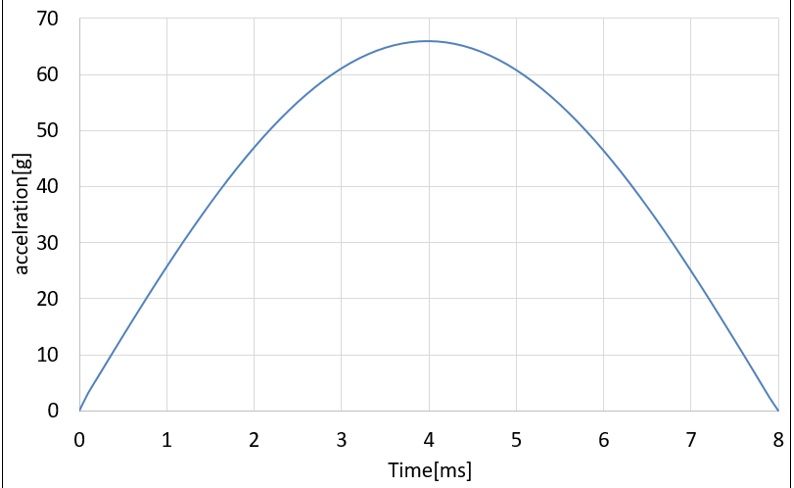
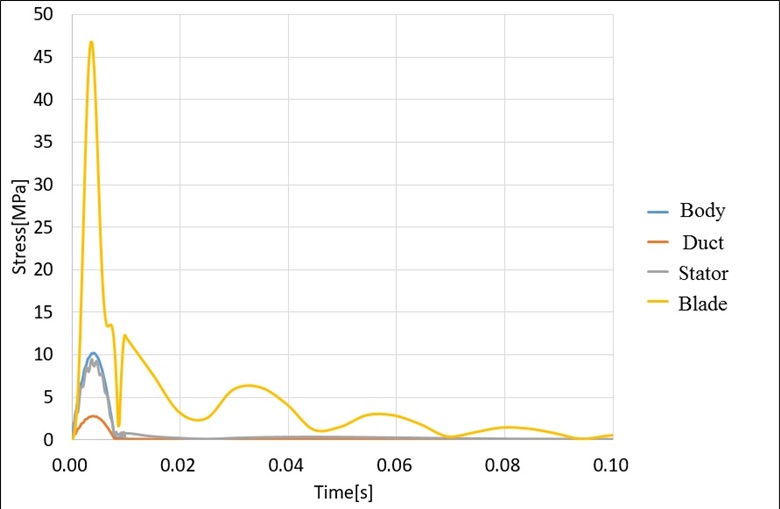
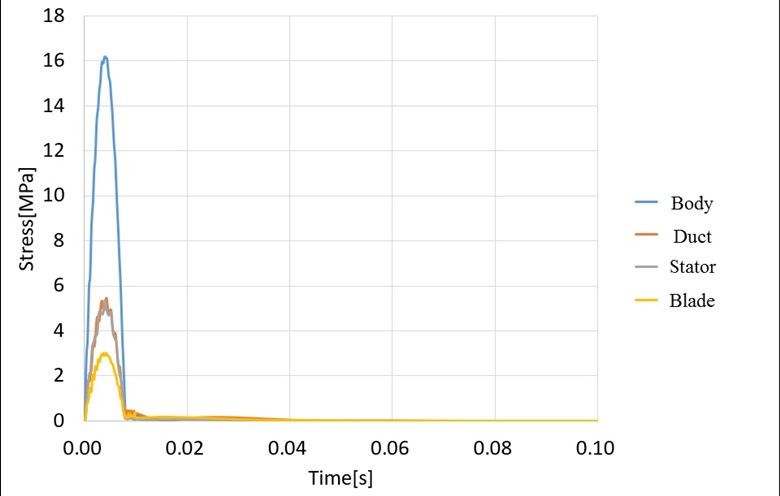
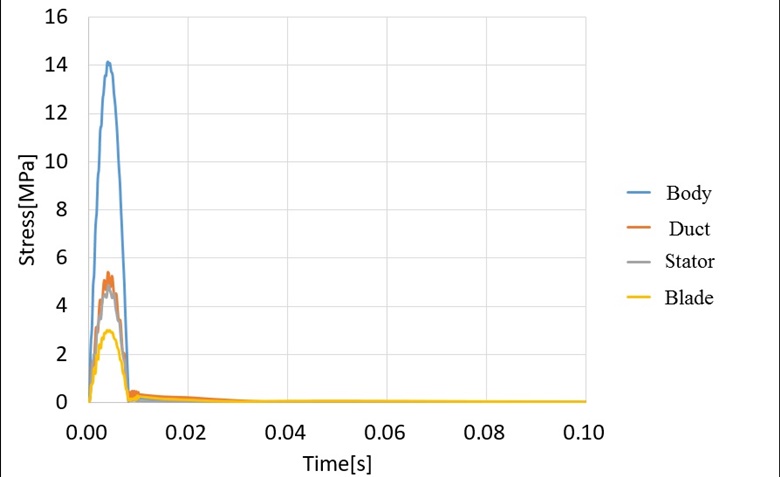
MIL-T-18404의 발사 조건에 대한 충격은 과도응답해석으로 진행된다. 크기 상한값을 입력값으로 인가하고 0.5초 동안의 등가응답을 확인하였다. Fig. 14는 충격 입력 값이며, Figs. 15 ~ 17은 X, Y, Z축 각각 과도응답 해석 결과이다. X축의 경우 블레이드에서 최대 46.8 MPa의 응력이 작용한다. Y, Z축의 경우 전방 몸체에서 최대응력이 작용하며, 그 값은 각각 16.2 MPa, 14.2 MPa이다. 앞서 언급한 바와 같이 Al6061-T6의 허용응력 240 MPa을 고려하였을 때, 최소 안전율 5.1 이상으로 충격해석 결과 구조적으로 안전한 설계가 된 것을 확인하였다.

Fig. 14

Shock input profile

Fig. 15

Result of shock analysis : X-axis

Fig. 16

Result of shock analysis : Y-axis

Fig. 17

Result of shock analysis : Z-axis

2.3 PVSS(Pseudo Velocity Shock Spectrum)

이 절에서는 PVSS의 개념을 설명하고, PVSS로 산출된 결과를 이용하여 구조 안전성을 분석하는 방법을 소개하였다. 대부분의 충격시험은 시간역의 가속도 값을 획득한다. 하지만 응력은 속도에 비례하기 때문에⁽¹¹⁾, 단순히 시간역에서 가속도 값의 평가는 충격 이벤트를 표현하기에 부족하다. 응력과 속도와의 관계는 식 (7) ~ (8)과 같다. 또한 PVSS는 하나의 그래프 상에 주파수에 대한 속도, 가속도, 변위를 한 번에 나타낼 수 있기 때문에 충격 이벤트를 이해하는 데 매우 유용한 상대변위 충격 스펙트럼의 표현이며, 장비의 잠재적인 손상 가능성을 판정하는 지표로써 주로 해군분야에서 널리 활용된다. 응력값을 획득하기 힘든 충격시험의 경우 가속도 값으로 PVSS를 계산하여 재료의 응력 및 위험속도를 산출 하지만 이 논문의 대상장비는 시험을 수행하지 않아 과도응답해석의 가속도 값을 이용하여 분석하였다.

F o r R o d, σ m a x = ρ c υ m a x

(7)

F o r B e a m, σ m a x = h η ρ c υ m a x

(8)

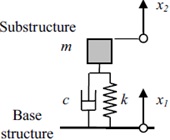
여기서, σ_max, ρ, c, υ_max, $h η$ 는 각각 최대응력, 밀도, 음속, 최대모달속도, 형상계수이다. 형상계수 중 η은 회전반경으로 (I/A)^0.5로 표현되며, I는 빔 중립축에 대한 단면적 관성모멘트, A는 단면적, h는 중립축에서의 거리이다. 단일 자유도 시스템을 가지는 Fig. 18의 운동방정식은 식 (9)와 같다. 여기서 m, c, k, x는 각각 질량, 감쇠, 강성, 변위이다.

m x ¨ 2 + c x ˙ 2 + k x 2 = c x ˙ 1 + k x 1

(9)

Fig. 18

SDOF system

식 (9)는 식 (10)과 같이 정리할 수 있으며, 식 (11)의 라플라스 변환(Laplace transform)에 의해 식 (12)의 상대변위 전달함수를 구할 수 있다.

m x ¨ 2 = - c x ˙ 2 - x ˙ 1 - k x 2 - x 1

(10)

L f' = s L f - f 0 L f'' = s 2 L f - s f 0 - f' 0

(11)

H s = X 2 s - X 1 s A 1 s = - m m s 2 + c s + k

(12)

식 (12)는 식 (13)에 의해 식 (14)와 같이 pseudo velocity SRS(shock response spectrum) 전달함수가 된다. 여기서 ζ, ω_n은 각각 감쇠비, 고유주파수이다⁽⁴⁾.

ω n 2 = k m 2 ζ ω n = c m

(13)

H s = - 1 s 2 + 2 ζ ω n s + ω n 2

(14)

Z-변환(Z-transform)에 의해 이산화하면 식 (15)와 같이 변형된다.

H z = β 1 z - 1 α 0 + α 1 z - 1 + α 2 z - 2

(15)

여기서 각 계수는 ISO 18431-4⁽¹²⁾ 규격에 의해 식 (16) ~ (19)와 같이 정의된다.

β 1 = - exp ⁡ A sin ⁡ B / B

(16)

α 0 = exp ⁡ 2 A

(17)

α 1 = - 2 exp ⁡ A cos ⁡ B

(18)

α 2 = 1

(19)

여기서, 계수 A와 B는 식 (20) ~ (21)과 같다.

A = ω n T s 2 Q

(20)

B = ω n T s 1 - 1 4 Q 2

(21)

PVSS는 식 (22)와 같이 상대변위와 고유주파수의 곱으로 표현되며, 식 (16) ~ (19)의 계수에 의해 계산할 수 있다.

P V i = ω i q i m a x

(22)

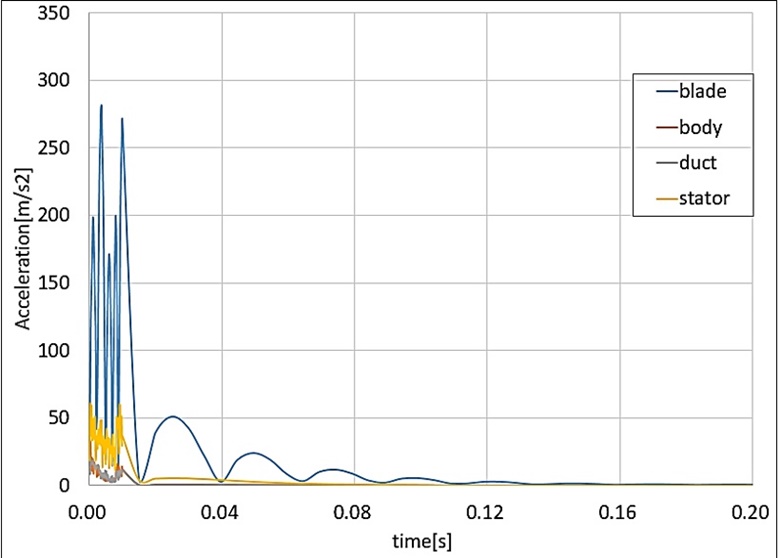
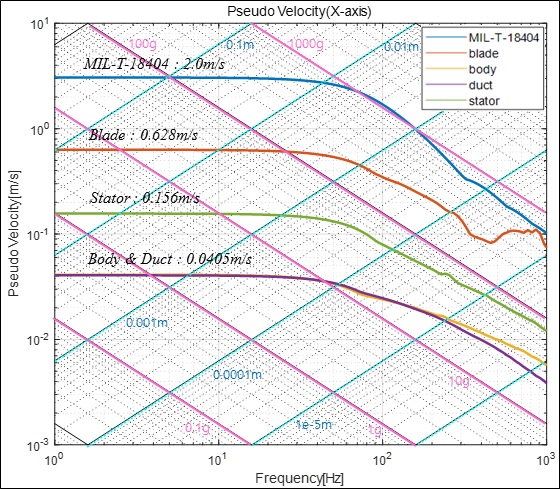
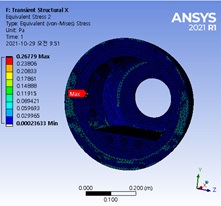
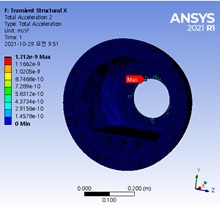
여기서, PV_i, ω_i, q_imax는 각각 pseudo velocity, 고유주파수, 최대상대변위이다. 2.2절의 과도응답해석으로부터 각 구성부에 발생하는 최대 가속도는 x축에서 발생하며, 그 값은 Fig. 19와 같다. Fig. 20은 MIL-T-18404의 과도응답 해석에 적용된 입력 가속도와 각 구성부 별 최대 가속도 값을 이용하여 최대 상대변위에 의해 계산된 PVSS이다. 과도응답해석과 PVSS에 의한 각 구성부의 응력 결과를 Table 6에 나타내었다. 두 결과의 응력 차이가 다소 많이 발생하는 것을 알 수 있다. 이는 앞서 언급한 바와 같이 가속도 결과로만 충격 이벤트를 충분히 표현할 수 없으며, Figs. 21 ~ 22와 같이 최대 가속도가 발생하는 위치와 최대응력이 발생하는 위치가 동일하지 않음을 알 수 있다. 따라서 시험을 통해 위험속도 및 최대응력을 확인하고자 할 경우에는 여러 지점에 센서를 부착하여 가속도 값을 획득해야 바람직한 결과를 얻을 수 있다. Table 7은 각 재료에 따른 위험속도이다. 재료의 위험속도를 알 수 있으면 응력을 산출하지 않아도 위험속도에 의한 잠재적 손상 판정지표로 안전성을 판단할 수 있다. 일부 재료에 따른 위험 속도를 Table 7에 나타내었다. 동일 재료이지만 형상계수에 따라 위험속도가 다른 것을 알 수 있다. 이 논문의 경우 최대 속도는 blade에서 0.63 m/s 값을 가지며, Al6061 재질로 최소 위험속도 10.5 m/s 대비 매우 낮은 수준으로 구조적으로 안전한 것을 알 수 있다.

Fig. 19

Acceleration results(X-axis)

Fig. 20

PVSS of input and output signals

Table 6

Stress results of PVSS and transient analysis

Fig. 21

Maximum stress position

Fig. 22

Maximum acceleration position

Table 7

Maximum stress modal velocities

3. 결 론

이 논문에서는 수중 무기의 추진체로 개발되는 일체형 추진장치가 운용 중 또는 수중폭발에 의해 받을 수 있는 진동 및 충격하중에 대한 구조 안전성 해석을 진행하였다. 진동의 경우 MIL-E-82590 규격에 의해 발생한 결과를 활용하여 내구성 관점의 피로해석을 수행하여 구조적으로 안전함을 확인하였다. 충격해석의 경우 수중폭발과 입수충격 해석으로 구분하여 수중폭발 내충격 설계의 경우 DDAM을, 입수충격의 경우 MIL-T-18404 규격에 의한 과도응답해석을 통해 구조적으로 안전한 것을 확인하였다. 또한 해군분야에서 널리 사용되는 PVSS 개념을 도입하여 충격시험을 통해 계측된 가속도 값을 이용하여 구조 안전성 분석 방법을 제안하였다. 이 논문에서는 추진체에 한해서만 분석을 하였지만 수중 무기 완성품에 적용되는 진동, 충격 환경조건이 동일하므로 언급된 해석 절차들은 수중 무기를 구성하는 각 구성부에도 동일하게 적용할 수 있을 것으로 판단된다.

기 호 설 명


c :	감쇠(Ns/m)
D_a :	충격 설계 값(m/s²)
k :	강성(N/m)
m :	질량(kg)
M_i :	질량 행렬(kg)
x :	변위(m)
X_ia :	변위 행렬(m)
ζ :	감쇠비
q_imax :	최대상대변위(m)
W_a :	모달중량 행렬(kg)
ω_n :	고유주파수(Hz)

Acknowledgments

이 연구는 방위사업청과 방위산업기술지원센터의 지원(일체형 추진장치 기술 연구, UC190005D) 하에 수행되었습니다.

References

MIL-T-18404, 1955, Military Specification Torpedoes, Environmental Requirement; General Specification for.
MIL-E-82590, 1970, Military Specification Environmental Requirement and Tests(For Torpedo MK 37 Components and Assemblies).
Moon, S. J., Kwon, J. I., Park, J. W., Chung, J. H. and Hwang, E. H., 2017, Validation, Verification and Accreditation of Measured Signal of Maximum Shock Pressure due to Underwater Explosion, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, No. 7, pp. 933~939. [https://doi.org/10.5050/KSNVE.2017.27.7.933]
Kim, C. K., 2000, Approximation Method to Estimate Water Entry Impact Forces Acting on Light Weight Torpedo, Journal of the Society of Naval Architects of Korea, Vol. 37, No. 2, pp. 77~87.
Kim, Y. W., Park, W. G. and Kim, C. S., 1999, Numerical Analysis of Impact Forces and Entry Behaviors of the High Speed Water Entry Bodies, Journal of Computational Fluids Engineering, Vol. 4, No. 1, pp. 1~7.
MIL-STD-901D, 1989. 3., Shock Tests. H.I.(High Impact) Shipboard Machinery, Equipment, and System, Requirements for.
O’Hara, G. J. and Belsheim, R. O., 1963, NRL Memorandum Report 1396, Interim Design Values for Shock Design of Shipboard Equipment.
ASTM B246-02a, 2002, Standard Specification For Aluminum And Aluminum-alloy Die Forgings, Hand Forgings, And Rolled Ring Forgings.
Hwa, P., 2001, Fatigue Behavior of 6061 Aluminium Alloy and Its Composite, M.S. Thesis, Dublin City University, Dublin, Ireland.
Kim, Y. and Song, O. S., 2006, Study for Characteristics of DDAM using MIL-S-901D Shock Test and Transient Response Analysis, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 16, No. 11, pp. 1132~1139. [https://doi.org/10.5050/KSNVN.2006.16.11.1132]
Gaberson, H. A. and Chalmers, R. H., 1969, Modal Velocity as Criterion of Shock Severity, The Shock and Vibration Bulletin, Bulletin 40, Part 2, pp. 31~64.
ISO 18431-4, 2007, Mechanical Vibration and Shock – Signal Processing – Part 4: Shock-response Spectrum Analysis.

Chang Min Lee is a research engineer at Mechanical Engineering R&D Lab, LIG Nex1. He received M.S. degree from Pusan National University. His research interests are shock/vibration.

Jae Yeop Choi is a research engineer at Mechanical Engineering R&D Lab, LIG Nex1.

Jung Hun Park is a research engineer at Mechanical Engineering R&D Lab, LIG Nex1.

Gwan Soo Jeon is a research engineer at Mechanical Engineering R&D Lab, LIG Nex1.

Freq. Range	Magnitude	Min. test time
10 Hz ~ 30 Hz	0.06 in ± 0.006 in	60 min
31 Hz ~ 60 Hz	3 ± 0.3 g	60 min
61 Hz ~ 100 Hz	3 ± 0.3 g	60 min

Submarines
Mounting location	Acceleration coefficient				Velocity coefficient			Shock direction	Elastic		Elastic-plastic
Mounting location	A_a	A_b	A_c	A_d	V_a	V_b	V_c	Shock direction	A_f	V_f	A_f	V_f
I. Hull	10.4	480.0	20.0	0.0	20.0	480.0	100.0	Vertical	1.0A₀	1.0V₀	1.0A₀	0.5V₀
								Athwartships	1.0A₀	1.0V₀	1.0A₀	0.5V₀
								Fore and Aft	0.4A₀	0.4V₀	0.4A₀	0.2V₀
II. Deck	5.2	480.0	20.0	0.0	10.0	480.0	100.0	Vertical	1.0A₀	1.0V₀	1.0A₀	0.5V₀
								Athwartships	2.0A₀	2.0V₀	1.0A₀	1.0V₀
								Fore and Aft	0.8A₀	0.8V₀	0.8A₀	0.4V₀
III. Shell plating	52.0	480.0	20.0	0.0	100.0	480.0	100.0	Normal to Hull	1.0A₀	1.0V₀	This is not permitted for this classification of equipment
								Tangential	0.2A₀	0.2V₀
								Fore and Aft	0.08A₀	0.08V₀

Surface ship
Mounting location	Acceleration coefficient				Velocity coefficient			Shock direction	Elastic		Elastic-plastic
Mounting location	A_a	A_b	A_c	A_d	V_a	V_b	V_c	Shock direction	A_f	V_f	A_f	V_f
I. Hull	20.0	37.5	12.0	6.0	60.0	12.0	6.0	Vertical	1.0A₀	1.0V₀	1.0A₀	0.5V₀
								Athwartships	0.4A₀	0.4A₀	0.4A₀	0.2V₀
								Fore and Aft	0.2A₀	0.2V₀	0.2A₀	0.1V₀
II. Deck	10.0	37.5	12.0	6.0	30.0	12.0	6.0	Vertical	1.0A₀	1.0V₀	1.0A₀	0.5V₀
								Athwartships	0.4A₀	0.4V₀	0.4A₀	0.2V₀
								Fore and Aft	0.4A₀	0.4V₀	0.4A₀	0.2V₀
III. Shell plating	40.0	37.5	12.0	6.0	120.0	12.0	6.0	Normal to Hull	1.0A₀	1.0V₀	This is not permitted for this classification of equipment
								Tangential	0.2A₀	0.2V₀
								Fore and Aft	0.1A₀	0.1A₀

Contents	Values
Density (kg/m³)	2700
Young’s modulus (GPa)	69.3
Poisson’s ratio	0.33
Damping ratio	0.0004

No. of mode	Frequency [Hz]
1	215
2	546
3	978
4	980
5	990
6	990
…	…
18	1227
19	1358
20	1491

Material	Velocity, rod [m/s]	Velocity, beam [m/s]
Al 5052	12.1	7.00
Al 6061	18.2	10.5
Cadmium	3.38	1.95
Copper	6.36	3.68
Nickel	8.07	4.67
Steel	6.09	3.52
Stainless	6.96	4.02
Titanium	33.2	19.2
Concrete	0.47	0.27

Component	PVSS [MPa]	Transient [MPa]
Blade	8.6	47
Stator	2.1	9.5
Body	0.6	10
Duct	0.6	2.8