[ Article ]

Transactions of the Korean Society for Noise and Vibration Engineering - Vol. 33, No. 1, pp.34-43

ISSN: 1598-2785 (Print) 2287-5476 (Online)

Print publication date 20 Feb 2023

Received 27 Sep 2022 Revised 02 Dec 2022 Accepted 15 Dec 2022

DOI: https://doi.org/10.5050/KSNVE.2023.33.1.034

파수-주파수 변환을 이용한 선체 벽면 압력으로부터 선박 추진기 압축성 압력 추출

하준범^* ; 구가람^** ; 정철웅^† ; 설한신^*** ; 정홍석^***

Extraction of Compressible Pressure due to Ship Propeller from Hull Surface Pressure Using Wavenumber-frequency Transformation

Junbeom Ha^* ; Garam Ku^** ; Cheolung Cheong^† ; Hanshin Seol^*** ; Hongseok Jeong^***

*School of Mechanical Engineering, Pusan National University, Student
**Center for Advanced Air-conditioning Refrigeration and Energy, Pusan National University, Researcher
***Korea Research Institute of Ships and Ocean Engineering, Senior Researcher

Correspondence to: ^†Member, School of Mechanical Engineering, Pusan National University, Professor E-mail : ccheong@pusan.ac.kr ‡ Recommended by Editor Han Shin Seol

Abstract

Underwater radiated noise (URN) is a compressible pressure component that propagates in the far-field from sources. Therefore, compressible pressure separation is required as a first step in developing a far-field URN monitoring technique based on hull surface pressure. In this study, a numerical method of decomposing surface total pressure induced by an underwater propeller into compressible and incompressible pressure was proposed using wavenumber-frequency transformation (WFT). First, a compressible multiphase Delayed Detached Eddy Simulation (DDES) of the hydrodynamic flow field was computed. Acoustic pressure caused by cavitation from the underwater propeller was predicted using the Ffowcs Williams–Hawkings (FW–H) integral equation and compared with the measured data to validate the numerical simulation. Finally, the compressible pressure was extracted from the total surface pressure on the stern part by using the WFT decomposition technique. In the high-frequency range, the compressible pressure appeared to be relatively high compared to the incompressible pressure in this study.

Keywords:

Underwater-radiated Noise, Hull Surface Pressure, Wavenumber-frequency Transformation, Compressible Pressure

키워드:

수중방사소음, 선체 표면 압력, 파수-주파수 변환, 압축성 압력

1. 서 론

선박에서 발생하는 수중방사소음은 발생하는 소음원에 따라 엔진류에 의한 기계적 소음과 선체와 추진기에 의한 유동소음으로 구분할 수 있다. 국가간 무역활동이 활발히 이루어지면서 해양운송 수단인 선박을 이용한 물류 운송이 늘어나고 물류 운송의 경제성을 높이기 위해 선박이 대형화와 고속화되는 추세이다. 이러한 추세는 고속 회전을 통해 추진성능의 증가를 수반하여야 하지만, 부수적으로 수중방사소음을 증가시키게 된다. 또한, 고속 회전에 따른 추진기에서의 국부적인 압력 저하는 다양한 형태의 공동 현상을 유발한다. 공동은 높은 레벨의 수중방사소음을 발생시켜 해양생태계의 음향신호 교란과 해양 생물의 집단 폐사 및 기형 물고기 발생과 같이 해양생태계에 악영향을 미치게 된다^(1~4). 이러한 해양생태계 환경오염 문제가 급속히 대두되고 있어 생태계 보호를 위해 국제해사기구(International Marine Organization, IMO)에서 수중방사소음에 대한 규제에 대해 논의하고 있다⁽⁵⁾. 이에 대응하기 위해 고성능 저소음 선박에 대한 연구가 활발히 이루어지고 있으며⁽⁶⁾, 특히 수중방사소음에 가장 큰 기여도를 가지는 추진기를 설계 단계에서부터 고성능, 저소음 설계를 진행하기 위한 다양한 연구가 활발히 이루어지고 있다.

Seol 등⁽⁷⁾은 단순 형상의 모형추진기를 이용하여 추진기 공동 관찰시험과 소음계측시험을 수행하였으며, 추진기의 공동 패턴에 따른 추진기 소음특성을 분석한 바가 있다. Park 등⁽⁸⁾은 대형 캐비테이션 터널에서 모형시험을 통한 추진기 수중방사소음을 계측하였으며, 이를 바탕으로 실선의 수중방사소음 추정한 바가 있다.

이와 같은 시험을 통한 연구는 시간과 비용적인 면에서 한계를 가지고 있어, 이를 보완하기 위하여 전산유체역학을 활용한 추진기 성능 평가 및 예측이 이루어지고 있다.

Park 등^(9~10)은 추진기 및 익형의 단독 성능 시험을 통해 날개 끝 와류 공동 추정에 영향을 미치는 날개 주위 유동장을 해석하였으며, 모형시험 계측결과와 비교 검증을 수행한 바가 있다. Seol 등⁽¹¹⁾은 유동해석을 통해 추진기 공동을 모사하고, 음향상사식을 통해 얇은 층 공동에 의한 추진기 날개 통과주파수(blade passing frequency, BPF)소음을 예측하였으며, 예측된 소음 결과를 중형 캐비테이션 터널에서의 실험결과와 비교 및 검증을 하였다. Ku 등^(12~13)은 고스큐 추진기를 대상으로 날개 끝 공동(tip vortex cavitation, TVC)과 공동소음을 보다 정확히 예측하기 위해 Eulerian – Lagrangian 단방향 연성 해석 기법을 개발하였으며, 날개 끝 와류 공동을 구형 공동기포로 모사하여 공동소음을 예측하였다. 또한 잠수함과 고스큐 추진기를 대상으로 격자 세밀화를 통한 유동해석을 수행하여 추진기 공동 유동을 모사하였고 사중극자 보정 FW-H 방정식⁽¹⁴⁾을 사용하여 추진기 소음을 예측하였고, 실험결과와 비교 및 검증을 하였다. Ha 등⁽¹⁵⁾은 추진기와 방향타간의 후류-익형 상호작용을 고려한 선박 수중방사소음 예측과 수중방사소음에 영향을 미치는 세부 구성품별 유동 소음원을 분석하였으며, 각 소음원이 미치는 영향에 대해 정량적으로 분석하였다. 이외에 많은 선행연구에서 수치 비용면에서 유리한 비압축성 가정을 적용한 공동 소음 예측 연구가 활발히 진행되었다^(16~23).

하지만 대부분의 연구는 수중 청음기가 시험영역에 국한되어 고정된 상태이기에 상시 모니터링 불가능하다. 또한 선내 계측 시에는 음압(acoustic pressure) 혹은 압축성 압력이라고 불리는 밀도의 섭동으로 인해 기인된 압력과 난류 속도장에 의하여 유체밀도의 섭동 없이 기인되어 수력학적 압력(hydrodynamic pressure), 대류압(convective pressure), pseudo sound라 불리는 비압축성 압력 섭동이 모두 계측되므로 실제 멀리 전파하는 압축성 압력만을 고려하기가 어렵다.

따라서, 이 연구에서는 실시간 수중방사소음 모니터링을 위하여 실선에서 측정 가능한 선체 벽면 압력을 입력값으로부터 원방으로 전파하는 선박 수중방사소음 성분인 압축성 압력을 추출하는 방법론을 제시하고 고찰하였다. 먼저, 유동 소음원을 보다 정확히 예측하기 위해 고정밀 해석인 delayed detached eddy simulation(DDES)을 적용하여 균일혼상류 가정의 압축성 유동해석을 수행하고 유동해석결과를 기반으로 Fowcs Williams and Hawkings(FW-H) 적분방정식을 통해 수중방사소음을 예측하였다. 유동해석, 소음해석 결과와 실험결과와의 비교를 통해 해석의 유효성을 확인하였으며, 이를 바탕으로 선체 선미부의 압력을 입력값으로 파수-주파수 변환을 통해 비압축성 압력과 압축성 압력을 분리하고 압축성 압력을 추출하였다.

논문 구성은 2장에서 수치해석 방법에 대해서 기술하였으며, 3장에서 수치해석 결과를 자세히 분석하였다. 이를 바탕으로 4장에서 결론을 제시하였다.

2. 수치해석 방법

2.1 해석 대상 및 경계 조건

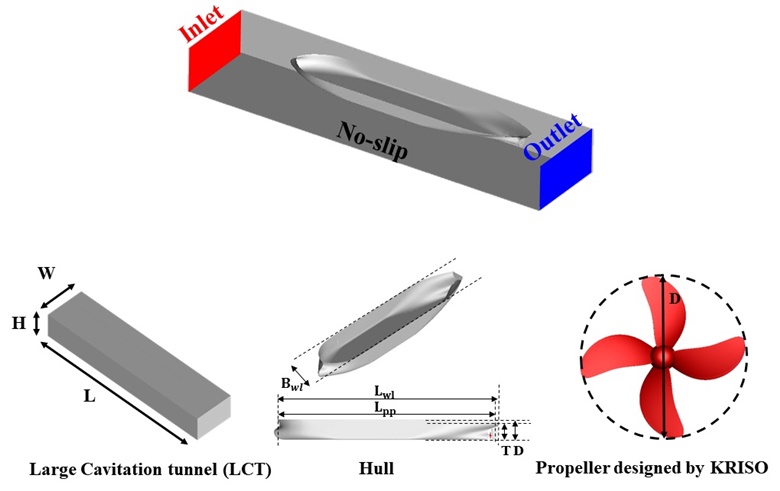
해석 대상으로 연구용 선체와 프로펠러를 고려하였으며, 선박해양플랜트연구소에서 수행한 모형 시험과 같은 경계조건을 적용하였다. 전체 계산영역은 대형 캐비테이션 터널 시험부와 동일한 조건으로 구성하였다. Fig. 1에 해석 대상과 영역을 나타내었으며, 관련 제원은 Table 1에 표시하였다. 경계조건은 입구부에 유속 7 m/s, 출구부에 게이지 압력 0 Pa로 설정하여 선체의 운항 속도를 모사하였으며, 추진기의 회전속도는 37.05 rps로 설정하였다. 시험부 벽면, 선체 벽면 그리고 추진기에서의 경계층 유동을 모사하기 위해 no-slip 조건을 설정하였다. 압축성 해석의 경우 출구부에 압축성 파가 반사되지 않도록 비반사 조건을 추가로 설정하였다. 격자 구성은 벽면에서의 경계층 유동을 잘 예측하기 위해 프리즘 격자를 구성하였으며, 추진기로 유입되는 선체의 반류장을 보다 정확히 모사하기 위해 선미 부근에 조밀하게 격자를 구성하였다. Fig. 2에 격자 구성을 나타내었으며, 터널 시험부와 선체의 y⁺는 30, 추진기는 무차원 벽면 거리 변수인 y⁺가 5 이하가 되도록 구성하였다. 총 1400만 개의 격자를 구성하여 수치해석을 수행하였다.

Fig. 1

Computational domain and geometries of numerical simulation

Table 1

Dimensions of LCT, hull and propeller

Fig. 2

Grids of computational domain, hull and propeller for numerical simulation

2.2 지배방정식 및 수치해석기법

이 연구는 상용프로그램인 ANSYS Fluent를 사용하여 균일혼상류모델의 이상유동해석을 수행하였다. 정상상태 RANS해석을 먼저 수행하고, 계산된 정상 유동을 초기조건으로 비정상 DDES 해석을 수행하였다. 식 (1) ~ (5)는 균일혼상류 RANS 지배방정식을 나타내었다.

∂ ρ m ∂ t + ∇ ρ m u i ¯ = 0,

(1)

∂ ∂ t ρ m u i ¯ + ∂ ∂ x j ρ m u i ¯ u j ¯ = ρ m g - ∂ p ¯ ∂ x i - ∂ ∂ x i ρ m u i' u j' ¯ + ∂ ∂ x j μ m ∂ u i ¯ ∂ x j + ∂ u j ¯ ∂ x i - 23 δ i j ∂ u k ∂ x k,

(2)

α l + α υ = 1,

(3)

ρ m = ρ υ α υ + ρ l α l,

(4)

μ m = μ υ α υ + μ l α l .

(5)

여기서, 아래첨자 m은 혼상류, l은 액체, υ는 증기를 의미하고, p, ρ, u, μ, α는 각각 압력, 밀도, 속도, 점성계수, 각 상의 체적분율을 나타낸다. ^-는 평균값이며, '는 변동값을 나타낸다. 공동 모델은 기포동역학 Rayleigh-Plesset 방정식을 기반으로 유도한 Schnerr-Sauer 모델을 적용하였으며, 난류 모델은 k-ω shear stress transport(SST)를 적용하였다. k-ω SST모델은 벽면에서는 k-ω 모델을 적용하여 경계층에서의 역압력 구배를 보다 잘 예측하고, 벽면이 아닌 그 외 영역은 k-ω 모델이 적용하여 계산을 수행한다. 선행연구^(15,17)를 통하여 Schnerr-Sauer 모델과 k-ω SST 난류 모델을 사용하여 추진기에서 발생하는 공동과 수중방사소음에 대한 예측결과의 유효성을 확인한 바가 있다. SST기반의 DDES는 벽면 근처의 경계층 내부는 RANS로 계산이 진행되고 경계층 이외의 영역은 large eddy simulation(LES)로 계산이 진행된다. 식 (6) ~ (8)에는 DDES의 이송방정식을 나타내었다.

∂ ρ k ∂ t + ∂ ρ U i k ∂ x i = ∂ ∂ x i μ + σ k μ t ∂ k ∂ x i + P k - ρ k 3 l D D E S,

(6)

∂ ρ ω ∂ t + ∂ ρ U i ω ∂ x i = ∂ ∂ x i μ + σ k μ t ∂ ω ∂ x i + 2 1 - F 1 ρ σ ω 2 1 ω ∂ k ∂ x i ∂ ω ∂ x i + α ρ μ t P k - β ρ ω 2,

(7)

l D D E S = l R A N S - f d m a x 0, l R A N S - l ≤ S,

(8)

식 (8)은 소산항의 길이 척도, f_d는 분포 함수, ν_T와 ν는 난류에 의한 동점성 계수, 매질의 동점성 계수, 그리고 k는 von Karman 상수를 의미한다. 그 외 식 (6) ~ (8)에 사용된 기호들은 참고문헌(24)에 정의된 것과 같다. 충분한 샘플링 주파수와 추진기에 의한 비정상 유동을 정확히 모사하기 위해 추진기 0.1° 회전시간인 7.497376 × 10^-6 s로 시간 간격을 설정하였다.

2.3 압축성 모델

이 연구에서 보다 현실적인 유동 모사와 파수-주파수 분석을 수행하기 위해 압축성 유동해석을 진행하였다. 유체의 압축성 반영은 에너지 방정식과 상태 방정식을 추가로 적용하여 반영하였다. 에너지 방정식은 식 (9)와 같다.

∂ ∂ t ρ m E + ∇ ⋅ υ → ρ m E + p = ∇ ⋅ k e f f ∇ T + S E, w h e r e E = h - - p ρ + υ 2 2

(9)

여기서 k_eff는 유효열전도율이고, S_E는 열원을 나타낸다. 물의 압축성은 다음의 상태 방정식인 Tait 방정식을 고려하였다.

ρ ρ 0 n = K K 0,

(10)

K = K 0 + n Δ P .

(11)

여기서 ρ, K는 액체의 밀도와 체적 탄성 계수를 나타낸다. 다음은 증기의 압축성을 고려할 수 있는 이상기체 방정식이다.

ρ = p o p + p R M w T .

(12)

식 (12) 기체 방정식을 통해 외부 압력에 의한 증기의 밀도와 체적 변화를 계산할 수 있다. R은 기체상수, M_ω은 분자량 그리고 T는 온도이다. 위의 에너지 방정식과 상태 방정식을 적용하여 압축성 수치해석을 수행하였다.

2.4 FW-H 음향상사법

이 연구에서 소음을 예측하기 위해 Lighthill의 음향사상법을 기반으로 하는 FW-H 방정식을 사용하였으며, 식 (13)에는 FW-H 방정식을 나타내었다.

4 π p' x, t = ∂ ∂ t ∫ S Q y, τ r 1 - M r d S y - ∂ ∂ x i ∫ S F i y, τ r 1 - M r d S y + ∂ 2 ∂ x i x j ∫ V T i j y, τ r 1 - M r d y . w h e r e Q = ρ u i' + U i - ρ 0 U i n i^F i = ρ u i' u j' + U j - p δ i j n i^T i j = ρ u i' u j' + p - p 0 - c 02 p - p 0 δ i j

(13)

여기서 x, y는 각각 수음점과 소음원의 위치이며, r은 수음점과 소음원의 거리이다. t, τ는 관찰자 시간과 지연시간이며, τ = t-r/c₀이다. M_r은 소음원에서 수음점 방향으로의 마하수를 나타내며, ρ, u, p는 각각 매질의 밀도와 속도, 압력을 의미한다. 상첨자 ”' ”는 섭동값, 하첨자 “₀”은 평균값을 의미하며, δ_ij는 Kronecker delta 함수, n은 적분면에서의 수직 벡터, c는 음속을 나타낸다. 식 (13)의 오른쪽 첫 번째 항은 시간변화에 따른 유체 체적 기인 소음원인 홀극 소음원을 의미하고 두 번째 항은 유체가 물체의 표면 압력 변화에 의한 소음인 쌍극 소음원, 마지막 항은 난류에 의해 방사되는 사중극자 소음원이다. 일반적으로 유동장 평균 속도가 저 마하수 유동일 때 난류 구조의 기여도는 효과가 미미한 것으로 알려져 있다. 사중극자 항을 무시한 홀극, 쌍극 소음원은 Farassat 1A공식에 의해 다음과 같이 나타낼 수 있다⁽²⁵⁾.

4 π p T' x, t = ∫ f = 0 ρ 0 U ˙ n + U n r 1 - M r 2 r e t d S + ∫ f = 0 ρ 0 U n r M ˙ r + c 0 M r - M 2 r 2 1 - M r 3 r e t d S

(14)

4 π p L' x, t = 1 c 0 ∫ f = 0 L ˙ r r 1 - M r 2 r e t d S + ∫ f = 0 L r - L M r 2 1 - M r 3 r e t d S + 1 c 0 ∫ f = 0 L r r M ˙ r + c 0 M r - M 2 r 2 1 - M r 3 r e t d S

(15)

w h e r e, U j = 1 - ρ ρ 0 υ j + ρ u j ρ 0 L i = P i j n^j + ρ u i u n - υ n

여기서 “^{^⋅}”와 “ret”는 시간 미분과 지연시간을 의미한다. 아래 첨자 n과 r는 수직방향과 수음점 방향을 나타내는 벡터이다.

p' x, t = p T' x, t + p L' x, t

(16)

이 연구에서는 식(16)과 같이 홀극( $p T ´$ )과 쌍극자( $p L ´$ ) 소음원만을 고려하였다.

2.5 파수-주파수 변환

파수-주파수 분석은 운송체 실내 소음에 대한 외부 유동의 기여도 평가 및 내부 유동에서의 기여도 평가 등 많은 연구에서 다뤄지고 있다^(26~28). 외부 유동으로 인한 벽면에서 형성되는 압력 섭동은 난류 경계층 유동에 의한 비압축성 압력과 외부 소음에 의한 압축성 압력으로 나눌 수 있다. 하지만 압축성 압력인 음파의 경우 대류에 의한 비압축성 압력에 비해 압력변동이 작아 표면 압력 섭동에서 압축성 압력을 바로 분리하기가 어렵다. 이 연구에서는 압축성 압력을 분리하기 위해 선체 선미부의 압력을 이용하여 푸리에 변환인 파수-주파수 변환을 사용하였으며, 시간 정보인 주파수와 공간 정보인 파수의 함수는 다음 식으로 나타낼 수 있다.

G ξ, τ = E p x, t p x + ξ, t + τ

(17)

여기서 x와 t는 공간과 시간을 의미하며, p, ξ 그리고 τ 는 각각 압력, 공간 지연, 시간 지연을 나타낸다. 파수-주파수 스펙트럼은 주파수와 파수로 표현되며 식 (20)과 같다.

S k x 1, k x 2, ω = ∫ - ∞ ∞ ∫ - ∞ ∞ ∫ - ∞ ∞ G ξ 1, ξ 2, τ e - j - k ξ 1 - k ξ 2 + ω τ d ξ 1 d ξ 2 d τ

(18)

압축성 압력을 3차원 스펙트럼에서 분리하기 위해 선체 선미부 표면을 따라 평행하게 전파하는 음향파의 정보로부터 식 (19) ~ (20)을 정의할 수 있다.

ω = c 0 k x 1 2 + k x 2 2 + k x 1 U 0

(19)

k a = ω / c 0 = k x 1 2 + k x 2 2 + k x 1 M

(20)

여기서, U₀는 평균 유속이며, M은 평균 유속에 대한 마하수를 나타낸다. 위 식을 통해 디락콘(dirac cone)을 나타낼 수 있다. 선미부 표면에서 음향 파수(acoustic wavenumber) k_a를 통해 디락콘으로 표시되는 영역 내부는 음속보다 빠른 영역인 압축성 압력으로 분리할 수 있으며, k ≤ k_a를 만족한다. 그 이외의 영역은 음속보다 느린 영역으로 k > k_a 이며, 음속이 아닌 영역이기에 비압축성 압력 섭동 영역으로 정의할 수 있다.

3. 수치해석 결과

3.1 유동해석 결과

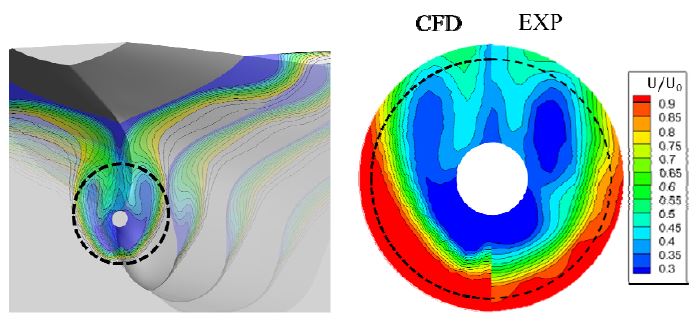
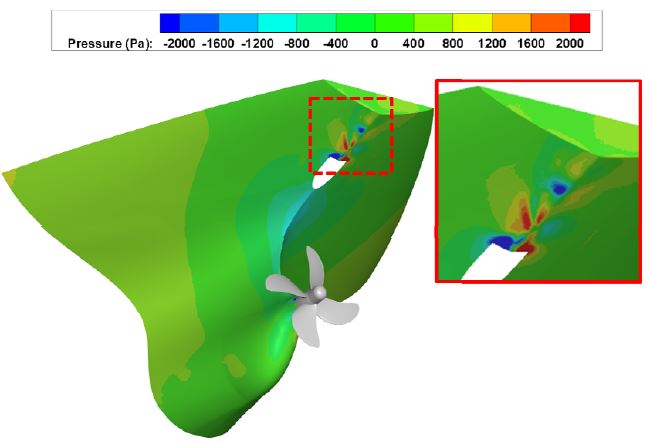
먼저, 추진기가 없는 선체(bare hull)에서의 RANS 정상상태 해석을 통해 선체 반류장을 확인하였다. Fig. 3은 선체 반류장을 축방향 유동에 대해 평균 유속으로 무차원화하여 나타내었다. 실험은 예인수조에서 측정된 반류장이며, 수치해석은 터널에서의 반류장이기 때문에 정확한 비교는 어려우나, 실험과 해석 모두 갈고리 형태의 유사한 유동분포를 확인할 수 있다. 반류장 확인 후, 추진기가 설치된 선체의 정상상태 해석을 수행하였고, 정상상태 해석을 초기조건으로 비정상 유동해석을 수행하였다. Fig. 4는 추진기에서 발생하는 공동을 체적 분율 α = 0.1에 대해 가시화하여 실험과 비교한 그림을 나타내었다. 두 결과 모두 터널 시험부 영역에서 수행되었으며, 각각 θ = 10°와 θ = 20°에서 비교하였다. Fig. 5는 선체 선미부의 압력 분포를 나타내었다. 선미부에서는 와류에 의한 압력변동이 명확하게 나타나지 않으며, 방향타 목을 지나면서 와류가 형성되어 비압축성 압력변동이 발생함을 알 수 있다. 이러한 결과를 미루어 볼 때, 선미부에서의 압력은 프로펠러 공동에 의한 압력변동이 지배적임을 알 수 있다.

Fig. 3

Hull wake-field at propeller plane

Fig. 4

Comparison of propeller cavitation between experimental result and compressible SST-DDES solver result

Fig. 5

Temporal pressure perturbation obtained from compressible SST - DDES solver results

3.2 유동소음 해석 결과

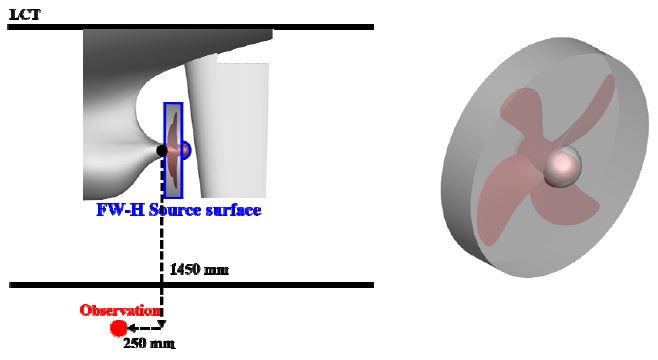
유동해석 결과를 입력값으로 FW-H 적분방정식을통해 소음해석을 수행하였다. 투과성 적분면은 Fig. 6과 같이 영역을 선정하여 유동해석과 동일한 시간 간격으로 필요한 정보를 추출하였다. 수음점의 위치는 Fig. 6과 같이 실험과 비교하기 위해 대형 캐비테이션 터널 수중 청음기와 동일한 위치로 설정하여 계산을 수행하였다. 소음 예측결과와 실험과의 유효성을 평가하기 위해 투과성 적분면으로부터 예측된 결과와 터널 시험결과를 1/3옥타브 밴드로 비교하였으며, Fig. 7에 나타내었다. 고주파에서 스펙트럼 경향과 에너지 수준이 잘 일치하는 것을 확인할 수 있으나, 저주파 영역에서는 실험 결과에 비해 소음해석 결과가 낮게 나타나는 결과를 확인할 수 있다.

Fig. 6

FW-H integral surface and observer location for noise analysis

Fig. 7

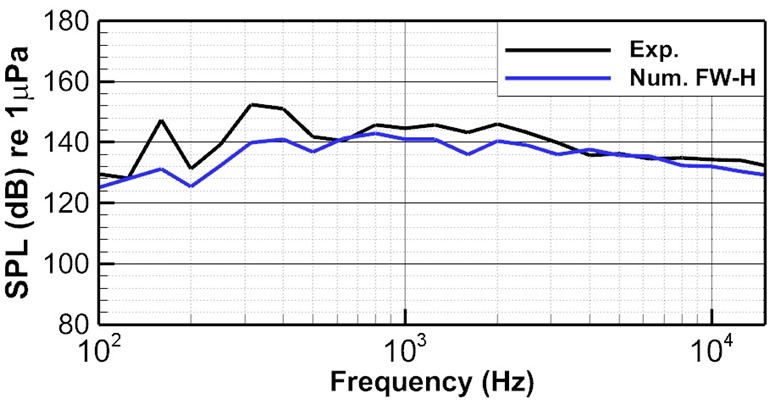
Comparison of predicted one-third octave band spectrum using permeable FW-H in compressible solver and experimental results

Fig. 7의 전체 음압 수준(overall sound pressure level, OASPL)을 Table 2에 표시하였다.

Table 2

Comparison of OASPLs between experimental and numerical results

3.3 파수-주파수 결과

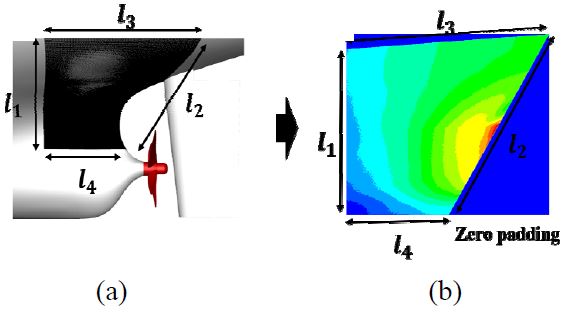
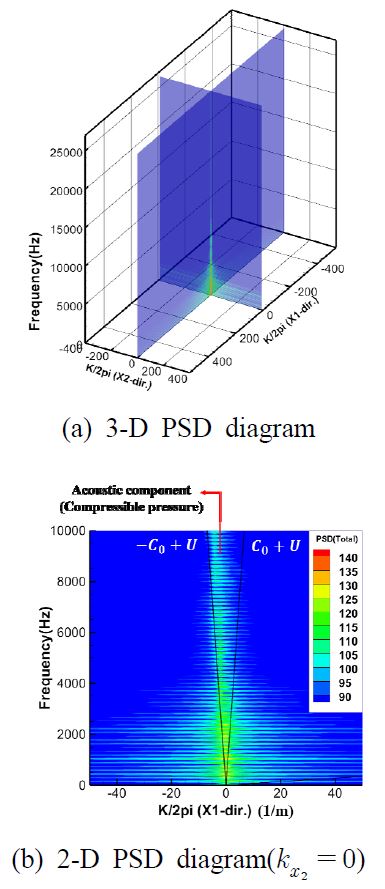
유동해석과 소음해석을 통해 해석의 유효성을 확인하였으며, 유동해석을 바탕으로 압축성 압력을 추출하기 위해 파수-주파수 변환을 수행하였다. 선미부의 압력은 유동해석과 동일한 시간 간격으로 추출되었으며, Fig. 8 (a)에 입력값으로 사용할 선미부의 영역을 나타내었다. 3차원 파수-주파수는 엄밀하게는 사각 평판 2차원 영역에 대해서 적용되기 때문에 이 연구에서는 Fig. 8의 곡면 형상을 1 mm의 등간격의 정렬 격자계 사각 평판으로 근사하였으며, 400 × 500개의 압력 신호를 사용하였다. 파수-주파수를 통해 계산된 파워 스펙트럼 밀도는 Fig. 9 (a)와 같이 파수-주파수 영역에서 나타낼 수 있으며, 파수 분해능은 △k_x = 1/(N_x△x)로 표현이 가능하다. N_x는 압력 신호의 개수이며, △x는 격자간의 거리이다. 디락콘(-c₀+U₀ ≤ ω/k ≤ c₀+U₀) 내부 영역은 압축성 압력이고, 나머지 영역은 비압축성 압력으로 볼 수 있다. 자세히 확인하기 위해 2차원 파워 스펙트럼 밀도 다이어그램(k_x₂ = 0)을 Fig. 9 (b)에 나타내었으며, 압축성 압력을 추출하는 기울기의 특성은 |-c₀+U₀|과 |c₀+U₀|이다. 여기서 c₀(= 1500 m/s)는 음속, U₀(= 7 m/s)는 평균 유속이다. 압축성 영역인 |-c₀+U₀|에 큰 레벨의 압력 성분들이 분포함을 확인할 수 있다. 압축성과 비압축성 압력은 명확하게 분리된 영역을 통해 추출할 수 있다. Fig. 10은 디락콘을 통해 분리된 압축성 압력과 비압축성 압력을 각각 역 파수-주파수를 적용하여 시계열 압력으로 계산하였으며, 특정 시간에서의 선미부 압축성 압력과 비압축성 압력을 나타내었다.

S ω = ∬ S k x 1, k x 2, ω d k x 1 d k x 2

(21)

Fig. 8

Configuration of computation domain of wavenumber-frequency transformation

Fig. 9

Power spectral density diagrams of Wavenumber-frequency transformation

Fig. 10

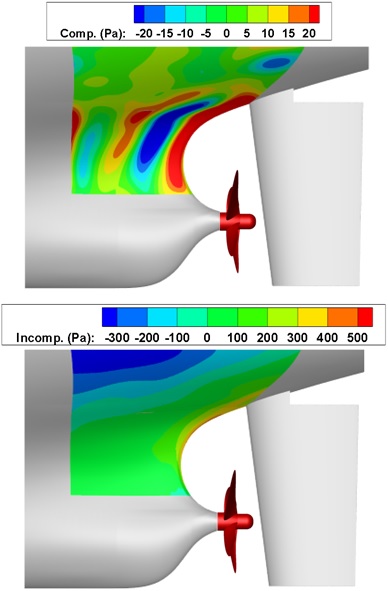
Decomposition of the surface pressure field: compressible pressure (top); incompressible pressure (bottom)

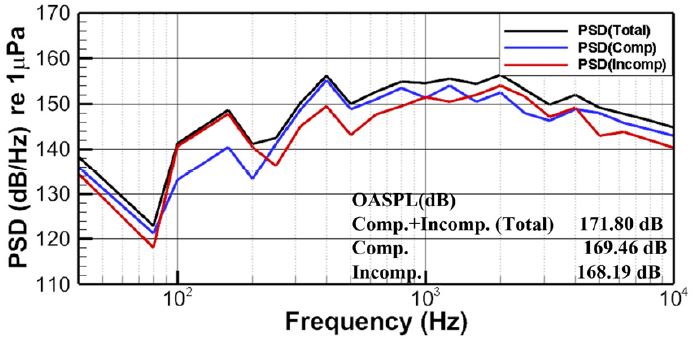
다락콘 내부의 압축성 압력과 디락콘 외부의 비압축성 압력의 스펙트럼은 식 (21)을 사용하여 파수영역 전체에 걸쳐 계산하였으며, Fig. 11에 스펙트럼을 나타내었다. 이 연구의 수치해석 조건에서는 압축성 압력이 저주파 영역을 제외한 고주파 영역에서 비압축성 압력에 비해 기여도가 상대적으로 다소 높게 나타남을 볼 수 있다.

Fig. 11

Comparison of the power spectral density levels by integrating wavenumber

4. 결 론

이 연구에서는 연구용으로 설계된 선체와 수중 추진기를 대상으로 압축성 유동해석을 수행하여 추진기 유동 소음원을 모사하고 소음을 예측하였다. 예측한 수중방사소음은 실험결과와의 비교를 수행하여 해석의 유효성을 확인하였다. 이후, 선미부 압력을 입력값으로 파수-주파수 변환을 이용하여 압축성 압력과 비압축성 압력을 분리하여 추출하였다.

유동 소음원을 보다 정확하게 모사하기 위해 압축성 SST-DDES 다상 유동해석을 수행하였다. 유동해석에서 계산된 반류장과 공동의 형상을 실험과 비교하였으며, 유동해석 결과를 바탕으로 추출된 투과성 적분면을 통해 예측된 수중방사소음 또한 파워 스펙트럼 밀도와 1/3옥타브 밴드로 나타내어 비교하였다. 유동해석과 소음해석을 통해 해석의 유효성을 확인하였으며, 유동해석을 바탕으로 파수-주파수 변환을 수행하였다. 파수-주파수 결과인 파워 스펙트럼 밀도 다이어그램에서 디락콘을 사용하여 비압축성 압력과 압축성 압력을 분리하였으며, 분리된 각 압력은 재구성하여 선미부에서의 압력 섭동을 확인하였다. 또한 비압축성 압력과 압축성 압력을 적분하여 파워 스펙트럼 밀도를 비교하였고, 이 수치해석의 조건에서는 압축성 압력의 기여도가 고주파 영역에서는 비압축성 압력에 비해 다소 높게 나타남을 확인하였다.

추후 연구에서 선미부 표면 압력으로부터 추출된 압축성 압력 신호를 사용하여 원방으로 전파하는 선체 수중방사소음을 예측 및 모니터링하는 기법을 개발할 예정이다.

Acknowledgments

이 연구는 산업통상자원부 지원 국가R&D사업 “IMO 해양환경보호 규제대응을 위한 선박 수중방사소음 모니터링 및 소음저감 기술개발(20012974)”로 수행된 연구결과입니다.

References

Fuentes, A. J., Suchy, M. and Palomo, P. B., 2019, The Greatest Challenge for URN Reduction in the Oceans by Means of Engineering, OCEANS 2019 MTS/IEEE SEATTLE. IEEE. [https://doi.org/10.23919/OCEANS40490.2019.8962779]
Williams, R., Wright, A. J., Ashe, E., Blight, L. K., Bruintjes, R., Canessa, R. and Wale, M. A., 2015, Impacts of Anthropogenic Noise on Marine Life: Publication Patterns, New Discoveries, and Future Directions in Research and Management, Ocean & Coastal Management, Vol. 115, pp. 17~24. [https://doi.org/10.1016/j.ocecoaman.2015.05.021]
Hawkins, A. D. and Popper, A. N., 2017, A Sound Approach to Assessing the Impact of Underwater Noise on Marine Fishes and Invertebrates, ICES Journal of Marine Science, Vol. 74, No. 3, pp. 635~651. [https://doi.org/10.1093/icesjms/fsw205]
Erbe, C., Dunlop, R. and Dolman, S., 2018, Effects of Noise on Marine Mammals, Springer, New York, NY, pp. 277~309. [https://doi.org/10.1007/978-1-4939-8574-6_10]
IMO, 2014, Guidelines for the Reduction of Underwater Noise from Commercial Shipping to Address Adverse Impacts on Marine Life, MEPC.
ITTC, 2015, Specialist Committee on Hydrodynamic Noise, Proceedings of 27th International Towing Tank Conference.
Seol, H. S., 2018, Experimental Study on the Cavitation Noise Characteristics of Model Propeller in Uniform Inflow, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 28, No. 6, pp. 728~734. [https://doi.org/10.5050/KSNVE.2018.28.6.728]
Park, C. S., Kim, G. D., Yim, G. T., Park, Y. H. and Moon, I. S., 2020, A Validation Study of the Model Test Method for Propeller Cavitation Noise Prediction, Ocean Engineering, Vol. 213, p. 107655. [https://doi.org/10.1016/j.oceaneng.2020.107655]
Park, I. R., 2016, RANS Analyses of the Tip Vortex Flow of a Marine Propeller, Journal of Computational Fluids Engineering, Vol. 21, No. 2, pp. 62~69. [https://doi.org/10.6112/kscfe.2016.21.2.062]
Park, I. R., Kim, J. I., Seol, H. S., Kim, K. S. and Ahn, J. W., 2018, Numerical Analysis of Tip Vortex and Cavitation of Elliptic Hydrofoil with NACA 662-415 Cross Section, Journal of Ocean Engineering and Technology, Vol. 32, No. 4, pp. 244~252. [https://doi.org/10.26748/KSOE.2018.6.32.4.244]
Seol, H. S., Park, C. S. and Kim, K. S., 2016, Numerical Prediction of Marine Propeller BPF Noise using FW-H Equation and Its Experimental Validation, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 6, pp. 705~713. [https://doi.org/10.5050/KSNVE.2016.26.6.705]
Ku, G., Cheong, C., Park, I. and Seol, H., 2020, Numerical Investigation of Tip Vortex Cavitation Inception and Noise of Underwater Propellers of Submarine using Sequential Eulerian–Lagrangian Approaches, Applied Sciences. Vol. 10, No. 23, p. 8721. [https://doi.org/10.3390/app10238721]
Ku, G., Cho, J., Cheong, C. and Seol, H., 2021, Numerical Investigation of Tip-vortex Cavitation Noise of Submarine Propellers using Hybrid Computational Hydro-acoustic Approach, Ocean Engineering, Vol. 238, p. 109693. [https://doi.org/10.1016/j.oceaneng.2021.109693]
Ku, G., Ryu, S. Y. and Cheong, C., 2018, Numerical Investigation into Cavitation Flow Noise of Hydrofoil using Quadrupole-corrected Ffowcs Williams and Hawkings Equation, Journal of the Acoustical Society of Korea, Vol. 37, No. 5, pp. 263~270.
Ha, J., Ku, G., Cheong, C., Seol, H., Jeong, H. and Jung, M., 2022, Investigation on Relative Contribution of Flow Noise Sources of Ship Propulsion System, Journal of the Acoustical Society of Korea, Vol. 41, No. 3, pp. 268~277.
Kim, S., Cheong, C., Park, W. G. and Seol, H., 2016, Numerical Investigation of Cavitation Flow around Hydrofoil and Its Flow Noise, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 26, No. 2, pp. 141~147. [https://doi.org/10.5050/KSNVE.2016.26.2.141]
Kim, S., Cheong, C. and Park, W., 2017, Numerical Investigation into the Effects of Viscous Flux on Cavitation Flow around Hydrofoil, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 27, pp. 721~729. [https://doi.org/10.5050/KSNVE.2017.27.6.721]
Kim, S., Cheong, C. and Park, W. G., 2017, Numerical Investigation on Cavitation Flow of Hydrofoil and Its Flow Noise with Emphasis on Turbulence Models, AIP Advances, Vol. 7, No. 6, p. 065114. [https://doi.org/10.1063/1.4989587]
Ha, M., Cheong, C., Seol, H., Paik, B. G., Kim, M. J. and Jung, Y. R., 2018, Development of Efficient and Accurate Parallel Computation Algorithm using Moving Overset Grids on Background Multi-domains for Complex Two-phase Flows, Applied Sciences, Vol. 8, No. 10, p. 1937. [https://doi.org/10.3390/app8101937]
Kim, S., Cheong, C. and Park, W. G., 2018, Numerical Investigation into Effects of Viscous Flux Vectors on Hydrofoil Cavitation Flow and Its Radiated Flow Noise, Applied Sciences, Vol. 8, No. 2, p. 289. [https://doi.org/10.3390/app8020289]
Ku, G., Cheong, C., Kim, S., Ha, C. T. and Park, W. G., 2017, Numerical Study on Cavitation Flow and Noise in the Flow around a Clark-Y Hydrofoil, Transactions of the Korean Society of Mechanical Engineers A, Vol. 41, No. 2, pp. 87~94.
Cho, J., Ku, G., Cheong, C. and Seol, H., 2020, Numerical Investigation of Cavitation Noise of the Submarine Propellers using DDES Technique and Quadrupole Corrected FW-H Equation, In INTER-NOISE and NOISE-CON Congress and Conference Proceedings, Vol. 261, No. 2, pp. 4376~4381.
Ku, G., Cheong, C. and Seol, H., 2020, Numerical Investigation of Blade Tip Vortex Cavitation Noise using Reynolds-averaged Navier-stokes Simulation and Bubble Dynamics Model, Journal of the Acoustical Society of Korea, Vol. 39, No. 2, pp. 77~86.
Gritskevich, M. S., Garbaruk, A. V., Schütze, J. and Menter, F. R., 2012, Development of DDES and IDDES Formulations for the k-ω Shear Stress Transport Model, Flow, Turbulence and Combustion, Vol. 88, No. 3, pp. 431~449. [https://doi.org/10.1007/s10494-011-9378-4]
Farassat, F., 2007, Derivation of Formulations 1 and 1A of Farassat (No. L-19318).
Vanherpe, F., Baresh, D., Lafon, P. and Bordji, M., 2011, Wavenumber-frequency Analysis of the Wall Pressure Fluctuations in the Wake of a Car Side Mirror, In 17th AIAA/CEAS Aeroacoustics Conference (32nd AIAA Aeroacoustics Conference), p. 2936. [https://doi.org/10.2514/6.2011-2936]
Kim, K. S., Ku, G. R., Lee, S. J., Park, S. G. and Cheong, C., 2017, Wavenumber-frequency Analysis of Internal Aerodynamic Noise in Constriction-expansion Pipe, Applied Sciences, Vol. 7, No. 11, p. 1137. [https://doi.org/10.3390/app7111137]
Lee, S., Cheong, C., Kim, B. and Kim, J., 2021, Comparative Analysis of Surface Pressure Fluctuations of High-speed Train Running in Open-field and Tunnel Using LES and Wavenumber-frequency Analysis, Applied Sciences, Vol. 11, No. 24, p. 11702. [https://doi.org/10.3390/app112411702]

Junbeom Ha received his B.S. in Mechanical Engineering from Pusan National University 2021. He is now a M. S. student in Mechanical Engineering at Pusan National University. His research interest is multi-phase flow, cavitation flow, and underwater noise.

Garam Ku received his B.S. in Aerospace Engineering from Pusan National University in 2015. He received his M.S. and Ph.D. degree in Mechanical Engineering from Pusan National University in 2017 and 2022. He is currently working at Agency for Defense Development. His research interests include multi-phase flow, propeller cavitation noise.

Cheolung Cheong received his B.S. in Mechanical and Aerospace Engineering from Seoul National University 1997. He received his M.S. and Ph.D. degree in Mechanical and Aerospace Engineering from Seoul National University in 1999 and 2003. He is now a professor at School of Mechanical Engineering at Pusan National University in Pusan, Rep. of Korea. Dr. Cheong's recent research interests include high-speed vehicle interior noise, two-phase flow noise, pipe-valve flow noise, and fan/compressor flow noise.

Hanshin Seol received his B.S. in Aerospace Engineering from Pusan National University in 1998. He received his M.S. and Ph.D. degree in Mechanical and Aerospace Engineering from Seoul National University in 2001 and 2005. He is now a principal researcher at Korea Research Institute Ships and Ocean Engineering in Daejeon, Korea. Dr. Seol’s current research interests include hydroacoustics, propeller noise and development of propeller noise reduction technology.

Hongseok Jeong received his B.S. and M.S. in Mechanical and Aerospace Engineering from Seoul National University in 2012 and 2014. He received his Ph.D. degree in Engineering and Physical Sciences at the University of Southampton in 2019. He is currently working at Korea Research Institute of Ships and Ocean Engineering. His research interest is identification and mitigation of propeller noise.

Parameter
Large cavitation tunnel	Width (W)	2.8 m
	Length (L)	12.5 m
	Height (H)	1.8 m
Hull	Length between perpendiculars (Lpp)	8.114 m
	Length on waterline (Lwl)	8.345 m
	Beam on waterline (Bwl)	6.338 m
	Depth (D)	0.712 m
Propeller	Diameter (D)	0.250 m
Propeller	# of blade (N)	4