강화학습 기반 제어 알고리즘을 통한 시간 지연을 갖는 구조물의 진동 제어 연구
© The Korean Society for Noise and Vibration Engineering
Abstract
The vibration control of a one-degree-of-freedom system was performed in this study using Deep Deterministic Policy Gradient (DDPG), a reinforcement learning method. A delayed control force compared to the target control force is applied to the system due to the dynamic characteristics of an actuator, such as a pneumatic spring. Reinforcement learning is a learning method that finds better behavior by learning by itself according to a reward function that is directly related to the learning goal without using a complex mathematical model for the system. Since the accelerometer is the most commonly used sensor in vibration measurement, we proposed a suitable learning excitation force and compensation function based on the acceleration data. The final learned policy was used to simulate the superior performance of the control force for various external forces. It was found from the numerical simulation that the vibration control based on the DDPG and reinforced learning is effective in suppressing vibrations.
Keywords:
Reinforcement Learning, Deep Deterministic Policy Gradient, Vibration Control키워드:
강화학습, 심층 결정론적 정책 경사, 진동제어1. 서 론
구조물의 진동 제어를 위한 제어기 설계에 있어서 해당 구조물을 수치적으로 모델링하는 과정이 필요하다. 그 과정에서 일반적으로 진동 제어에 사용하는 액추에이터의 동특성까지는 고려하지 않는다. 이런 이유로 이론 모델과 실제 모델의 제어기 성능은 많은 차이가 날 수 있다. 대표적으로 공압을 사용하는 공기스프링은 입력 전압에 따라 공압이 들어갔다 나갔다 하는 시간이 필요하기 때문에 입력 변위와 실제 출력 변위와의 시간 차이가 발생하게 된다. 이 시간 지연은 공기스프링을 제어 액추에이터로 사용할 때 제어 성능을 악화시키고, 특히 제어 주파수 대역이 고주파일 때 오히려 구조물의 진동을 더 크게 만들 수 있다. 따라서 공압 액추에이터를 사용하여 진동을 제어하기 위해서는 액추에이터의 동특성을 고려하여야 하는데, 공기의 압축성으로 인해 비선형의 성질을 가지는 액추에이터를 모델링하는 과정이 매우 복잡하다. 또한 같은 액추에이터라도 제작이나 조립 과정에서 동특성이 달라질 수 있기 때문에 이론적으로 모든 동특성을 고려한다는 것은 쉽지 않다. 산업체에서 PID 제어기가 대표적으로 사용되고 있지만 공압 제진대와 같이 다수의 액추에이터를 사용하는 경우 적절한 이득값을 튜닝하는 과정은 많은 시행 착오가 필요하다. 하지만 강화학습을 사용하면 정확한 시스템을 파악할 필요 없이 제어 알고리즘을 학습시킬 수 있다. 또한 이득값 튜닝도 필요 없어서 다수의 액추에이터를 사용할 때에도 적합한 제어기라고 말할 수 있다.
최근 진동제어에 있어 강화학습을 사용하는 연구가 보이기 시작했다. 먼저 인공 신경망을 사용하지 않은 간단한 형태의 강화학습을 진동 제어 장치에 적용한 연구들이 이루어졌다. Wang(1)은 강화학습을 사용해 active mass damper(AMD)의 주파수 튜닝을 진행했다. Park 등(2)은 강화학습을 사용해 동흡진기의 강성을 제어함으로써 구조물의 진동을 저감하는 연구를 진행했다. 최근 연구들은 더 복잡한 진동 문제들을 해결하기 위해 인공 신경망을 사용한 강화학습을 적용하고 있다. 특히 연속적인 행동공간을 갖는 문제에 적합하다고 알려져 있는 deep deterministic policy gradient(DDPG)라는 강화학습 방법이 대표적으로 사용되고 있다. Qiu 등(3)은 PZT 압전 세라믹이 부착되어 있고 한쪽이 고정된 유연한 판의 진동 제어를 DDPG를 사용해 진행했다. DDPG 방법을 활용한 자동차의 현가장치에 대한 연구도 다양하게 이루어졌다(4,5). Yoo(6)는 MATLAB/SIMULINK 프로그램으로 DDPG를 사용해 이송 질량에 의해 가진 되는 공압 제진대의 진동 제어를 시뮬레이션 했다. 해당 연구는 공압 제진대의 3축의 변위와 기울기가 목표 값만큼 작아지도록 보상함수를 설정했다. 그러나 진동 계측에 있어서 가속도계가 가장 광범위하게 사용되고 있는 감지기이기 때문에 이 연구에서는 조금 더 실용적인 학습을 위해 가속도 데이터로 학습을 진행하였다. 가속도 데이터로 학습을 진행하게 되면 변위 데이터를 사용했을 때에는 발생하지 않는 정적 불안정성(static-instability)이 발생할 수 있다. 정적인 힘이 가해지면 변위 데이터 상에서는 힘에 대한 변위가 반영이 되어 보여지지만 가속도 데이터 상에서는 확인이 되지 않기 때문이다. 따라서 가속도 데이터를 사용하기 위해서는 변위 데이터 사용시와는 다른 학습 기진력과 보상 함수가 필요하다.
이 연구에서는 시간 지연을 갖는 액추에이터를 포함한 일자유도 모델의 진동 제어를 강화학습 중 DDPG 알고리즘을 사용해 진행했다. 그리고 가속도 데이터를 사용한 효과적인 학습을 위해 적절한 외력의 형태와 상태 파라미터 형태 및 보상 함수 설정방법을 제안하였다.
2. 강화학습
강화학습(reinforcement learning)은 기계학습의 한 방법으로 에이전트와 환경이 상호작용하며 행동을 교정해가는 학습이다. 에이전트는 행동하는 개체를 의미하는데 진동 제어에 있어서 에이전트는 보상(reward)과 상태(state)정보를 받아 제어력을 내보내는 제어기 부분에 해당하고, 환경은 그를 제외한 모든 부분이 해당된다. 처음에 에이전트는 어떤 행동을 해야 하는지에 대한 정보 없이 행동한다. 해당 행동이 환경에 영향을 주면 환경은 다시 에이전트에게 다음 상태와 보상에 대한 정보를 보내준다. 그 보상이 좋은 행동인지 판단하는 기준이 되어 강화학습은 결국 누적 보상을 최대로 만들기 위해 시행착오를 통해 특정 상태에서 어떤 최적의 행동을 취할지 정해주는 정책(policy)을 학습한다.
강화학습에는 다양한 에이전트가 존재한다. 그중에서 이 연구에서는 DDPG를 사용했다. DDPG는 Lillicrap 등(7)에 의해 처음 소개되었는데 연속적인 행동공간과 상태공간에 적합한 에이전트이다. DDPG는 model-free로 행동에 따라 환경이 어떻게 바뀔지 모르는 상태에서 사용 가능한 에이전트이다. 또다른 특징은 배우-비평가(actor-critic) 방식으로 두개의 네트워크를 가지고 정책함수와 가치함수를 모두 사용한다는 것이다. 여기서 가치는 환경과 행동이 어느 정도의 누적 보상을 갖게 될지에 대한 기댓값을 의미하며 함수 형태는 인공 신경망을 사용한다. 비평가 네트워크 Q(S, A)는 상태 S와 행동 A를 입력 받아 정책함수의 가치를 평가하고, 배우 네트워크 μ(S)는 상태 S를 입력 받아 비평가 네트워크의 평가를 기반으로 행동 A를 결정한다. 추가적으로 Q(S, A), μ(S) 네트워크 업데이트의 안정성을 위해 각각의 타깃 네트워크인 Q’(S, A), μ'(S)가 존재한다. DDPG는 off-policy 방법을 사용하는데 off-policy란 학습의 대상인 타깃정책과 실제로 환경과 상호작용하며 경험을 쌓는 행동정책이 다른 경우를 의미한다. 따라서 과거의 경험을 재사용해서 학습할 수 있는데 이를 위해 리플레이 버퍼(replay buffer)를 사용한다.
이 연구에서 사용한 DDPG 학습의 알고리즘은 다음과 같다. 학습에 앞서 먼저 4개의 네트워크를 초기화 해준다. Q 네트워크의 파라미터 값인 θQ를 무작위 값으로 초기화 해주고 Q’의 파라미터인 θQ'도 동일한 값으로 초기화 해준다. μ와 μ'의 파라미터인 θμ, θμ'도 동일한 무작위 값으로 초기화 해준다. 매 시간단계(time step) t마다 식 (1)을 통해 행동을 계산한다.
| (1) |
여기서 N은 노이즈 성분으로, 행동 선택에 있어서 노이즈를 추가함으로써 새로운 행동을 탐구할 수 있다. At를 실행하고 환경으로부터 보상 Rt과 다음 상태인 St+1의 정보를 받는다. 해당 경험 (St, At, Rt, St+1)을 경험 버퍼에 저장한다. 그 후 경험 버퍼에서 무작위로 M개의 경험 (Si, Ai, Ri, Si+1)을 선택해 Q 네트워크 업데이트를 위한 가치 함수 타겟인 yi계산에 사용한다. yi는 보상과 미래에 받게 될 누적 보상에 감쇠 요소(discount factor) γ을 곱한 값의 합으로 계산되는데 이를 식으로 표현하면 식 (2)와 같다.
| (2) |
그 후 손실함수를 최소화하는 방향으로 Q 네트워크를 업데이트한다. 손실함수는 식 (3)과 같이 정의된다.
| (3) |
μ 네트워크는 policy gradient를 사용한 식 (4)를 사용해 업데이트한다.
| (4) |
∇ μ(Si)Q(Si, Ai)는 μ에서 계산된 행동에 대한 Q출력의 gradient이고, ∇ θμμ(Si)는 μ 네트워크의 파라미터에 대한 μ출력의 gradient이다. 마지막으로 타겟 네트워크인 Q’, μ'의 파라미터를 θQ, θμ를 사용해 업데이트 하는데, 이때 식 (5)와 같이 smoothing factor τ를 사용해 조금씩 업데이트한다.
| (5) |
이 과정은 매 시간단계마다 실행되며 한 에피소드가 끝날 때까지 진행된다.
3. 시뮬레이션
3.1 모델링
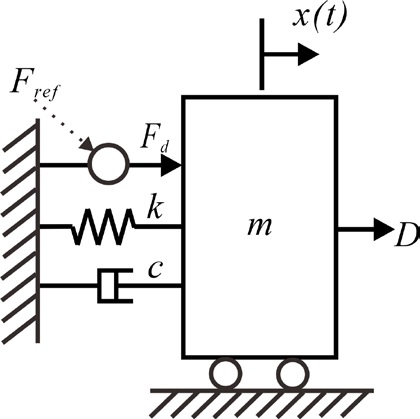
학습에 사용한 구조물 모델은 Fig. 1과 같이 액추에이터의 반응성으로 인해 입력 신호대비 지연된 액추에이터 출력을 가지는 1자유도 모델로 설정했다.
운동방정식은 다음과 같이 표현할 수 있다.
| (6) |
| (7) |
여기서 m, c, k는 각각 질량, 댐핑 계수, 스프링 상수를 나타내며, x는 질량 m의 변위이다. Fref는 액추에이터에 입력되는 제어 신호이며, Fd는 액추에이터의 시간 지연으로 인해 Fref신호에서 시간 td만큼 지연된 제어력을 의미한다. 모델링에 있어 액추에이터의 동특성 중 시간 지연만 고려하였기에 식 (7)와 같이 표현이 가능하다. D는 외력을 의미한다. 식 (7)를 식 (6)에 대입하고 질량 m으로 나누어 주면 다음과 같다.
| (8) |
여기서
| (9) |
3.2 시뮬레이션
시뮬레이션은 MATLAB/SIMULINK 프로그램을 사용해 진행했다. 학습에 사용된 파라미터는 Table 1과 같다.
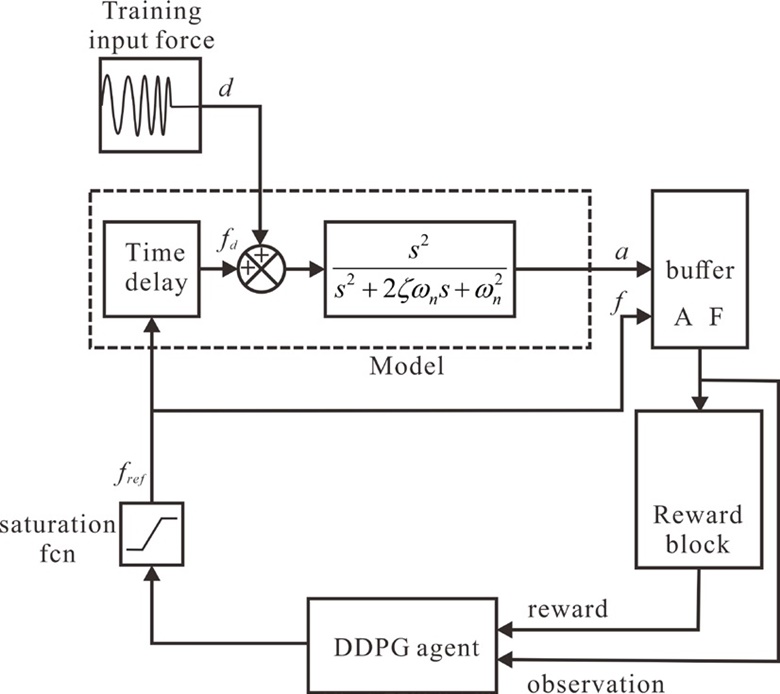
SIMULINK 프로그램을 블록 다이어그램으로 표현하면 Fig. 2와 같다.
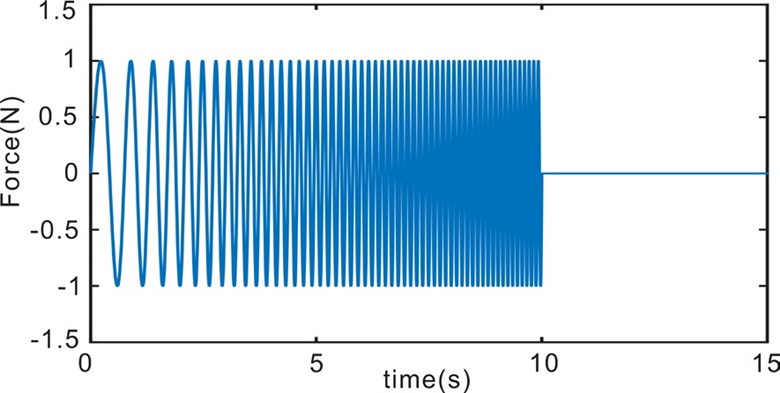
구조물이 고유진동수와 동일한 조화기진력을 받게 될 경우 공진 현상으로 인해 가장 위험하기 때문에 이 논문에서도 조화 기진력을 중점적으로 제어하도록 학습을 구성했다. 강화학습은 처음 접하는 환경에서 기대하는 성능이 나오지 않기 때문에 학습 환경 구성이 중요하다. 구조물의 고유진동수인 5 Hz에서 뿐 아니라 다양한 진동수의 조화 기진력에 대해서도 제어가 가능하도록 학습 기진력은 주파수가 10초간 1 Hz에서 10 Hz까지 변하는 사인 스윕파(sine sweep)를 사용했다. 그 후 힘이 작용하지 않을 때 발생하는 정적 불안정성을 제거하고자 10초에서 15초까지의 기진력은 0으로 설정했다. 최종적인 학습 기진력은 Fig. 3과 같은 형태이다.
상태는 가장 최신의 가속도 100개와 DDPG 에이전트에서 나온 제어력 99개로 설정했다. 즉 샘플링 주파수가 100 Hz이므로 1초 동안의 가속도와 제어력을 상태로 설정했는데 이는 이 연구에서 다루는 문제를 강화학습에 적합한 형태인 마르코프한 문제로 만들어 주기 위함이다.
강화학습의 리워드는 학습의 방향성을 설정하는 유일한 수단으로 어떻게 설정하느냐에 따라 학습 결과가 달라진다. 리워드는 스칼라의 값이 되어야 하기 때문에 학습 목표들의 적절한 결합으로 표현되어야 한다. 이 연구에서의 학습 목표는 진동이 제어되는 것이기 때문에 시스템의 가속도 값의 root-mean-square(rms) 성분이 작을수록 리워드가 커지게 설정하였다. 또한 제어력의 rms값과 평균값이 작을수록 리워드가 커지게 설정해 주었는데, 이는 빠르게 최적의 힘 크기를 찾고 정적 불안정성을 제거하도록 하기 위함이다. 세 성분의 선형 결합의 계수는 여러 번의 시도를 통해 최적의 값을 찾았고, 리워드의 최종 식은 식 (5)와 같다.
| (10) |
여기서 arms는 가장 최신의 100개의 가속도 값들의 rms 값이다. frms과 faverage는 가장 최신의 99개의 제어력의 rms 값과 평균값을 의미한다.
3.3 결과
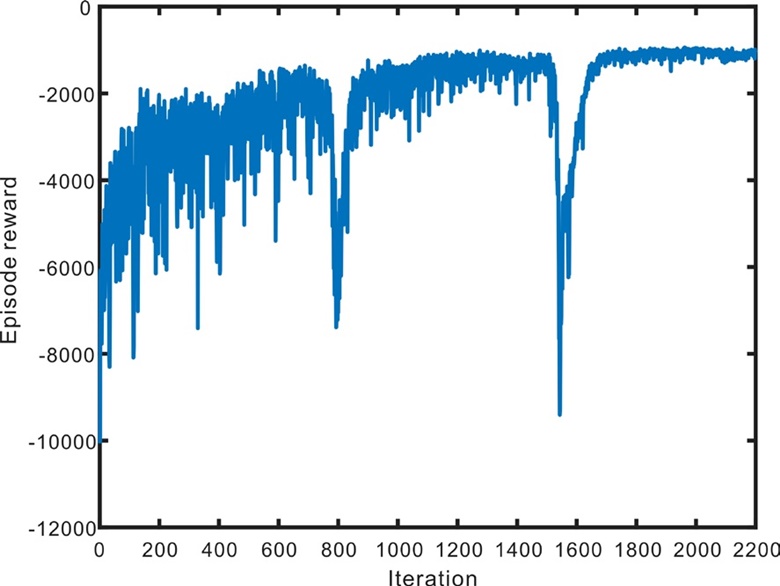
학습 에피소드 진행에 따른 보상은 Fig. 4와 같다. 학습을 반복할수록 보상의 값이 커졌기 때문에 좋은 정책을 찾아갔다고 해석할 수 있다. 학습을 계속해서 진행해본 결과 무조건적으로 학습을 많이 반복한다고 보상이 계속해서 수렴하는 것이 아니라, 과적합(overfitting)이 발생하며 급격히 제어 성능이 하락하는 것을 확인했다. 따라서 보상의 최댓값은 -950정도로 확인되었지만 안정적인 제어기 학습을 위해 -1000이라는 보수적인 보상 목표 값을 설정했다. 따라서 학습은 100번 동안의 보상 평균이 -1000이 되었던 에피소드의 정책을 최종 정책으로 선택하였다. 결론적으로 2200번대 에피소드의 정책이 선택되었다.
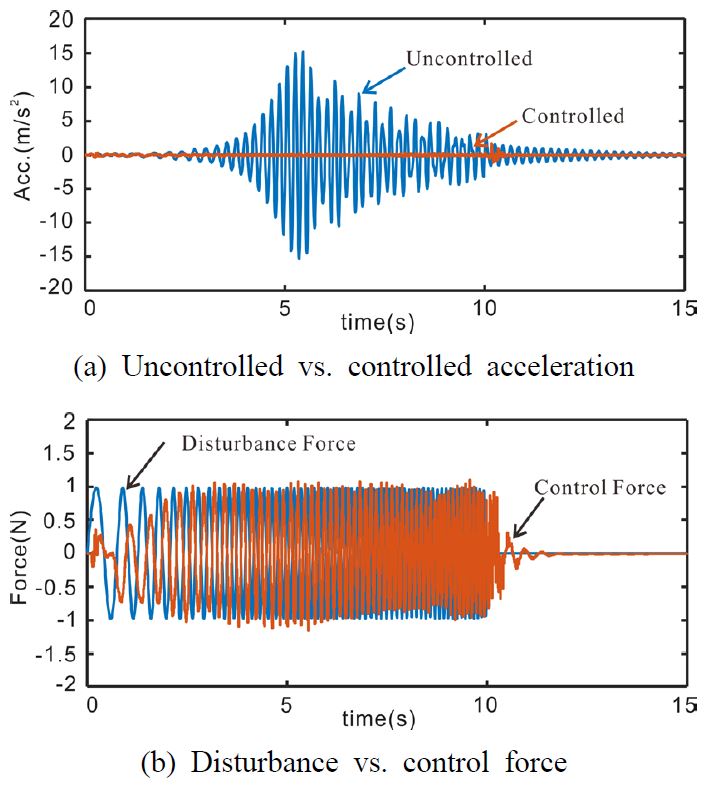
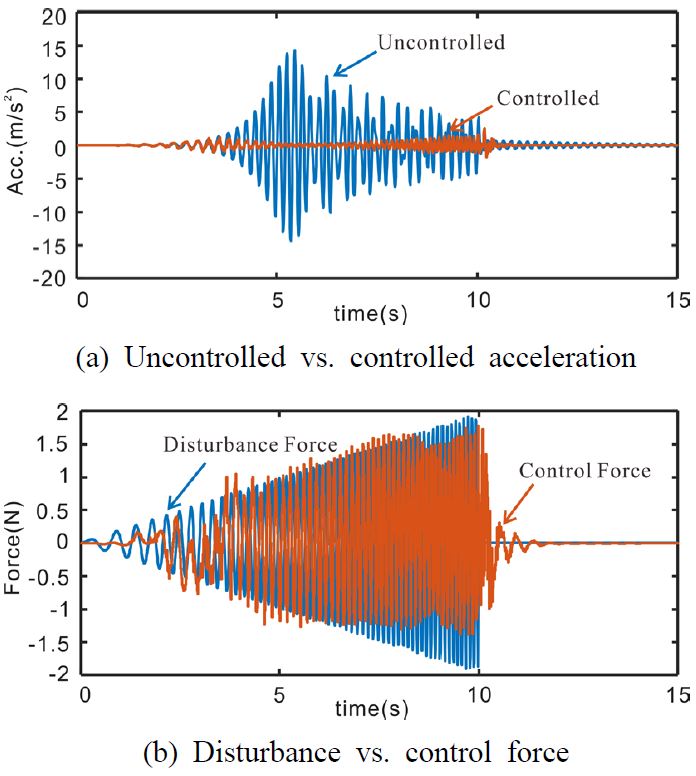
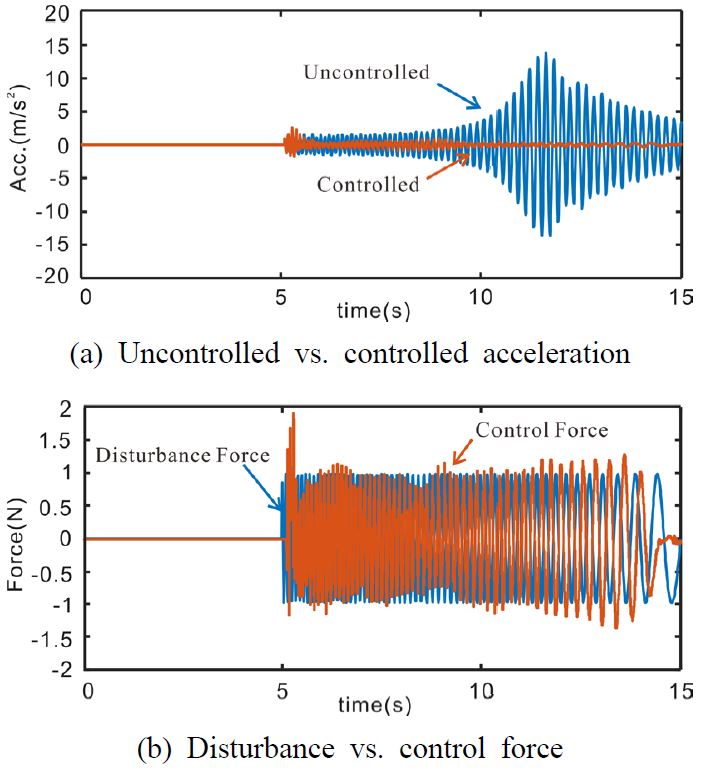
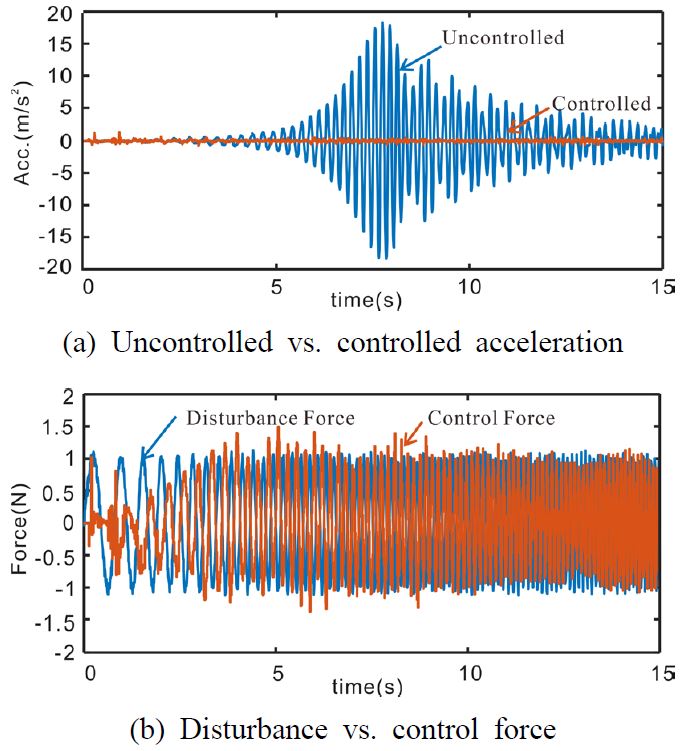
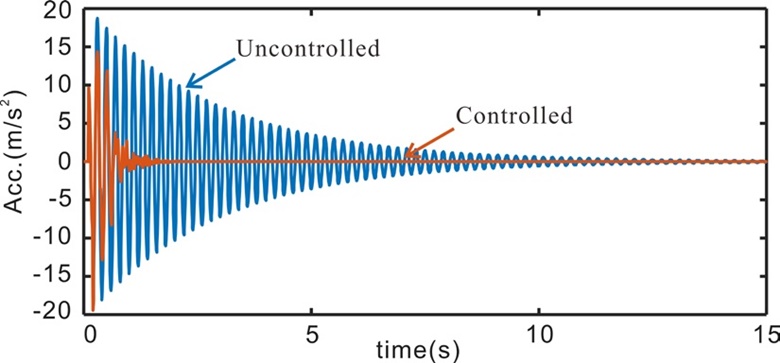
최종 정책을 사용하여 5가지 종류의 기진력을 입력하여 결과를 확인함으로써 제어기의 성능을 확인했다. Case 1은 Fig. 3의 학습 기진력을 시스템에 입력한 경우이다(Fig. 5). Case 2는 학습된 진폭 이외의 진폭에 대해서도 제어가 가능한지를 확인하기 위해 학습 기진력이 진폭이 0에서 2까지 점진적으로 커지는 형태로 만들었다(Fig. 6). Case 3는 학습 기진력과는 반대의 기진력이 가해졌다. 즉, 정지 신호가 먼저 존재하고 10 Hz에서 1 Hz으로 변하는 사인 스윕파를 기진력으로 사용했다(Fig. 7). Case 4는 실제 실험에서 발생할 수 있는 노이즈에 대한 영향을 확인하고자 사인 스윕파에 노이즈가 추가된 형태의 기진력을 입력했다(Fig. 8). Case 5는 구조물에 큰 충격이 가해진 경우이다(Fig. 9).
4. 결 론
이 연구에서는 액추에이터의 동특성으로 인해 목표하는 제어력에 비해 지연된 제어력이 인가되는 일자유도 시스템의 진동 제어를 강화학습의 한 방법인 DDPG를 사용해 진행했다. 진동 계측에 있어 가장 대표적으로 사용되는 가속도 센서의 데이터를 그대로 사용하기 위해 상태와 보상함수를 적절한 형태로 구성하였다. 변위 데이터에서는 발생하지 않지만 가속도 데이터를 사용할 때는 발생하는 정적 불안정성을 제거하기 위해 추가적인 보상 요소를 사용하였으며, 적절한 학습 기진력 형태를 제안했다. 2000번가량의 학습을 거친 최종 정책으로 5가지 기진력을 대상으로 제어 성능을 확인했다. 5가지 기진력은 학습 기진력을 응용한 형태로 구성했다. 확인 결과 해당 기진력들에 대해서도 우수한 성능을 보여주었다. 특히 하나의 진폭에 대해서만 학습을 진행했음에도 불구하고 다른 진폭의 기진력이 입력되었을 때에도 ± 50 %의 진폭에서는 비슷한 제어 성능을 보여주었다. 그러나 ± 50 % 이외의 진폭의 힘이 가해지는 경우에는 기대하던 성능이 나오지 않았다. 이처럼 강화학습은 학습해보지 않은 상황에서는 어떤 결과가 나올지 예상할 수 없다. 그렇기에 안정성이 중요한 진동 분야에 적용하기에는 한계가 있다고 판단된다. 이러한 문제를 해결하기 위해서는 최대한 다양한 경우에 대해 학습을 진행해야 하고, 그에 따른 효율적인 학습 환경 구성이 필요하다. 향후 연구에서는 외란의 형태, 크기, 구조물의 특성을 다양하게 구성하여 더 많은 상황에 대해 제어가 가능하도록 할 필요가 있다. 또한 이 연구에서는 시뮬레이션을 통해 가속도 신호를 사용한 구조물의 진동 제어에 대한 가능성을 확인하였기에, 추후 연구에서는 실험을 진행하여 실제 구조물에서의 강화학습 기반 진동 제어를 연구할 필요가 있다.
Acknowledgments
이 연구는 2022년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(20011159).
References
-
Wang, X., 2020, Coarse-fine Self-learning Active Mass Damper for Frequency Tracking Vibration Control, International Journal of Structural Stability and Dynamics, Vol. 20, No. 2, p. 2050024.
[https://doi.org/10.1142/S0219455420500248]

-
Park, J. E., Lee, J. and Kim, Y.-K., 2021, Design of Model-free Reinforcement Learning Control for Tunable Vibration Absorber System based on Magnetorheological Elastomer, Smart Materials and Structures, Vol. 30, No. 5, 055016.
[https://doi.org/10.1088/1361-665X/abee35]

-
Qiu, Z.-C., Chen, G.-H. and Zhang, X.-H., 2021, Reinforcement Learning Vibration Control for a Flexible Hinged Plate, Aerospace Science and Technology, Vol. 118, 107056.
[https://doi.org/10.1016/j.ast.2021.107056]

-
Kim, Y. J., Hong, S. M. and Oh, J. S., 2022, Design of Control Algorithm for Micro Electric Vehicle Suspension System using Reinforcement Learning Algorithm, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 2, pp. 124~132.
[https://doi.org/10.5050/KSNVE.2022.32.2.124]

-
Liu, M., Li, Y., Rong, X., Zhang, S. and Yin, Y., 2020, Semi-active Suspension Control based on Deep Reinforcement Learning, IEEE Access. Vol. 8, pp. 9978~9986.
[https://doi.org/10.1109/ACCESS.2020.2964116]

- Yoo, S. J., 2022, A Study on Pneumatic Isolation Table Vibration Control Excited by Moving Mass using Reinforcement Learning, M.S. Thesis, Hanyang University, Seoul, Korea.
- Lillicrap, T. P., Hunt, J. J., Pritzel, A., Heess, N., Erez, T., Tassa, Y. and Wierstra, D., 2015, Continuous Control with Deep Reinforcement Learning, arXiv Preprint arXiv:1509.02971, .

Soo-Min Kim received B.S. in Mechanical Engineering from Dongguk University in 2020. She is currently a graduate student in the Dept. of Mechanical Engineering in Dongguk University. Her research interests are active vibration control and fluid-structure interaction.

Moon Kyu Kwak received B.S. and M.S. degrees in Naval Architecture from Seoul National University in 1981 and 1983. He then received his Ph.D. degree from the Dept. of Engineering Science and Mechanics of Virginia Tech in 1989. He is currently a Professor at the Department of Mechanical, Robotics and Energy Engineering of Dongguk University in Seoul, Korea. His research interests are dynamics and control of flexible multibody system and active vibration control of smart structure.

Soo-Chul Lim received the B.S., M.S. and Ph.D. degrees in mechanical engineering from the Korea Advanced Institute of Science and Technology, Daejeon, South Korea, in 2001, 2003, and 2011, respectively. From 2006 to 2009, he was a full-time Lecturer with the Department of Mechanical Engineering, Korea Military Academy. From 2011 to 2016, he was a Research Staff Member with the Samsung Advanced Institute of Technology. He is currently an Associate Professor with the Department of Mechanical, Robotics, and Energy Engineering, Dongguk University, Seoul, South Korea. His current research interests include human–robot interaction, machine learning, surgical robot, and haptics.