입자 충돌 댐퍼를 장착한 시스템의 진동 해석 및 실험

1. 서 론

최근 공학 분야에서는 현대 인간의 삶의 수준을 고려한 다양한 기술이 개발되고 있다. 그러나 기계 시스템과 장비의 사용에는 불가피한 요소가 작용하는데, 그 중 하나는 진동과 소음이다. 이 연구에서는 다양한 시스템의 진동과 소음을 억제하는데 효과적인 입자 충돌 댐퍼(particle impact damper; PID)를 고려하였다.

입자 충돌 댐퍼는 구조물이 진동할 때 진폭이 가장 크게 발생하는 부분에 입자를 담은 용기를 부착하여 구조물의 진동을 억제하는 댐퍼이다. 구조물이 운동할 때 입자가 운동 에너지를 흡수하여 자유롭게 이동하며 용기내 충돌이 발생된다. 이때 충돌로 인하여 마찰력이 발생하고 진동이 감쇠된다.

입자 충돌 댐퍼는 점탄성(visco elastic) 댐퍼와 달리 광범위한 온도에서 작동할 수 있기 때문에 사람의 손길이 닿지 못하는 가혹한 환경에서 사용할 수 있고, 시스템의 특성과 용도에 따라 설계를 할 수 있기 때문에 넓은 범위의 주파수에 적용이 가능하며, 반영구적인 사용이 가능하기 때문에 경제적이면서도 효과적인 댐퍼라고 할 수 있다.

입자 충돌 댐퍼는 1940년대 Lieber and Jensen⁽¹⁾이 항공기 플러터 현상 제어를 연구하면서 단일 입자를 담은 충돌 댐퍼로 처음 소개되었다. 이후 Masri^(2,3)는 주기당 양쪽으로 입자가 두 번 충돌할 때 충돌 댐퍼가 안정적으로 동작하는 것을 주장하였고 정현파에 의해 감쇠되는 1자유도 시스템의 엄밀해를 정의하고 그 안정성을 분석하였다. Masri and Ibrahim⁽⁴⁾은 Runge Kutta 방법을 사용하여 입자 충돌 댐퍼의 동작을 수치적으로 해석하고 임의의 가진에 의한 1자유도계 응답을 분석했다. Bapat and Sankar⁽⁵⁾는 자유 및 강제 진동 하에서 단일 입자 충격 댐퍼의 응답을 연구하였다. 시뮬레이션을 위하여 엄밀해를 이용한 수학적 모델을 정의하였고 실험을 진행하였다. 입자와 시스템의 질량비가 댐퍼의 감쇠력과 비례하는 것과 반발 계수 및 용기 내 간격이 일정 수치보다 커지면 감쇠 효과가 줄어드는 것을 입증했다. Papelou and Masri^(6~8)는 다중 입자를 담은 입자 충돌 댐퍼의 운동 방성식을 풀기 위해 다중의 입자를 동일한 질량을 가진 동등한 단일 입자로 대체하여 분석적 해를 계산하여 시스템의 수치 해석을 진행하였다. 마찬가지로 Friend and Kinra⁽⁹⁾는 입자를 덩어리 질량으로 표현하여 다중 입자 댐퍼의 운동에 대한 분석적 접근 방식을 개발하고 중력, 진동 진폭 및 입자와 용기 사이의 간격 거리의 영향을 제시하였다. Yang 등⁽¹⁰⁾은 단일 충돌 댐퍼를 활용하여 레일 진동 저감 연구를 진행하였고 시스템의 수치해석을 위하여 Runge-Kutta 방법을 사용하였다. Lu 등⁽¹¹⁾은 이산요소법(DEM)을 이용한 입자 충돌 댐퍼의 수치해석법을 제안하였다. 이산요소법은 각각의 입자의 모션 및 시스템과 충돌로 인한 상호작용을 모두 반영하여 거동을 수치적으로 분석하는 해석 방법이다. 그러나 이산요소법으로 시스템 해석을 구현하려면 많은 리소스와 시간이 소요된다.

충돌로 인한 비선형 운동으로 인해 입자 충돌 댐퍼의 운동을 정확하게 해석하기에는 어려움이 있다. 이산요소법을 이용한 해석법은 오랜 시간이 걸리기 때문에 다각적인 방면에서 시뮬레이션을 거쳐야하는 입자 충돌 댐퍼 설계에 응용하기에는 아직 적합하지 않다. 그렇기 때문에 다중입자를 단일 입자 모델로 변환하고 시스템의 거동을 시뮬레이션하는 방법으로 연구가 진행되어왔다.

이 연구에서는 여러 개의 입자가 일렬로 정렬된 입자 충돌 댐퍼를 장착한 시스템의 거동을 비교적 간단한 방법으로 예측할 수 있는 알고리즘을 개발하였다. 알고리즘을 입증하기 위하여 볼베어링 구슬을 담은 입자 충돌 댐퍼를 장착한 1자유도계 실험 모델을 제작하여 실험을 진행하고 시뮬레이션 결과와 실험 데이터를 비교하였다.

2. 입자 충돌 댐퍼 메커니즘

2.1 충돌 알고리즘

서론에서 이야기하였듯이 용기 내에서 발생하는 입자의 충돌로 인하여 진동이 감쇠된다. 입자의 충돌은 용기 내벽과의 충돌이 될 수도 있고 다른 입자와의 충돌이 될 수가 있다. 주 시스템과 입자가 운동할 때 충돌이 발생하는 시점은 초기 정지 상태의 용기 내벽 사이 중점을 원점으로 설정하여 주 시스템의 변위, x_s와 입자의 변위, x_p를 측정하였을 때 왼쪽에 있는 물체의 변위가 오른쪽에 있는 물체의 변위보다 커지기 시작할 때로 정의 할 수 있다. 충돌하는 물체는 입자와 또 다른 양 옆의 입자가 될 수 있고, 용기의 왼쪽 내벽 혹은 오른쪽 내벽이 될 수 있다.

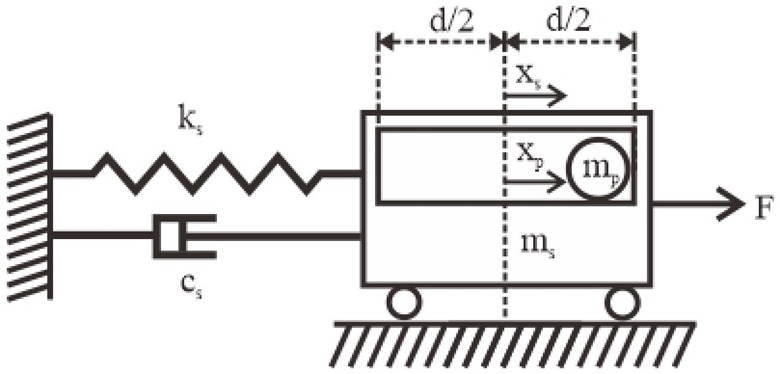
단일 입자 충돌 댐퍼의 1자유도계 모델을 Fig. 1과 같이 질량-감쇠-강성 모델로 표현하였다. 주 시스템의 질량, 감쇠, 강성을 m_s, c_s, k_s로 표현하고 입자 한 개의 질량을 m_p, 외력을 F라 표현하였다. 그림과 같이 용기 내벽 사이의 거리를 d라고 가정하였을 때 왼쪽 내벽과 오른쪽 내벽의 변위는 다음과 같이 표현할 수 있다.

$\[ x_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}=x_s-d/2 \]$

(1)

$\[ x_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}=x_s+d/2 \]$

(2)

Fig. 1

Schematic of PID system with single particle

입자의 반지름을 r_p라 하였을 때 입자의 변위와 양쪽 내벽의 변위를 이용하여 다음과 같은 충돌 발생 시점을 정의할 수 있다.

$\[ x_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l} }\ge x_p-r_p \]$

(3)

$\[ x_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l} }\le x_p+r_p \]$

(4)

입자의 변위가 왼쪽 내벽의 변위 보다 낮거나 같을 때, 혹은 오른쪽 내벽의 변위보다 크거나 같을 때 충돌이 발생한다. 입자 여러 개가 일렬로 있을 때도 같은 방식으로 충돌 알고리즘을 설정할 수 있다. 이 경우 입자의 개수에 따라 충돌이 가능한 모든 경우를 고려해 주어야 한다. 입자가 한 개씩 늘어날 때마다 충돌 가능한 경우의 수는 하나씩 늘어나며 이를 알고리즘에 반영해야 한다. 입자 두개를 담은 댐퍼의 경우 왼쪽부터 첫번째로 위치한 입자의 변위를 x_p1이라 하고, 두번째 입자의 변위를 x_p2라 하면, 충돌이 발생하는 경우는 다음의 세 가지 경우다.

$\[ x_{\mathrm{l}\mathrm{e}\mathrm{f}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l}}\ge x_{p1}-r_{p1} \]$

(5)

$\[ x_{p2}-r_{p2}\le x_{p1}+r_{p1} \]$

(6)

$\[ x_{\mathrm{r}\mathrm{i}\mathrm{g}\mathrm{h}\mathrm{t}\mathrm{w}\mathrm{a}\mathrm{l}\mathrm{l} }\le x_{p2}+r_{p2} \]$

(7)

충돌이 발생하는 경우를 집약적으로 표현한다면 왼쪽에 있는 물체를 A, 오른쪽에 있는 물체를 B라하였을 때 A의 변위, x_A가 B의 변위, x_B보다 크거나 같을 때로 정의 할 수 있다.

$\[ if x_B\le x_A\to \mathrm{c}\mathrm{o}\mathrm{l}\mathrm{l}\mathrm{i}\mathrm{s}\mathrm{i}\mathrm{o}\mathrm{n} \]$

(8)

2.3 수치 해석

시스템의 거동을 해석하기 위하여 상태방정식을 활용하였다. 주 시스템과 입자의 운동방정식을 정의하고 상태방정식으로 변환하여 수치 해석을 진행하였다. 또한, 입자가 움직일 때 발생하는 회전 관성 모멘트를 반영하였는데, 입자 한개의 질량관성 모멘트식은 다음과 같다.

$\[ I=\frac{2}{5}{m}_p{r}_p^2 \]$

(12)

식 (12)를 외력이 가해지는 1자유도계 운동방정식에 반영하면 다음과 같이 쓸 수 있다.

$\[ \left(m_s+\frac{2n_p}{5}{m}_p\right){\ddot{x}}_s+c_s{\dot{x}}_s+k_s{x}_s=F \]$

(13)

여기서 n_p는 입자의 개수이며 입자 하나의 운동방정식은 다음과 같이 표현된다.

$\[ m_p{\ddot{x}}_p=0 \]$

(14)

수치 해석을 위해서 주 시스템의 운동방정식을 연속 시간 상태 방정식으로 표현하면 다음과 같다.

$\[ {\dot{\mathbf{z}}}_s={\mathbf{A}}_{cs}{\mathbf{z}}_s+{\mathbf{B}}_{cs}F \]$

(15)

여기서

$\[ {\mathbf{z}}_s=\left[\begin{array}{c}{x}_s\\ {\dot{x}}_s\end{array}\right] \]$

(16a)

$\[ {\mathbf{A}}_{cs}=\left[\begin{array}{cc}0& 1\\ -\frac{k_s}{m_s+\frac{2n_p}{5}{m}_p}& -\frac{c_s}{m_s+\frac{2n_p}{5}{m}_p}\end{array}\right] \]$

(16b)

$\[ {\mathbf{B}}_{cs}=\left[\begin{array}{c}0\\ \frac{1}{m_s+\frac{2n_p}{5}{m}_p}\end{array}\right] \]$

(16c)

입자의 연속 시간 상태방정식은 다음과 같다.

$\[ {\dot{\mathbf{z}}}_p={\mathbf{A}}_{cp}{\mathbf{z}}_p \]$

(17)

여기서

$\[ {\mathbf{z}}_p=\left[\begin{array}{c}{x}_p\\ {\dot{x}}_p\end{array}\right] \]$

(18a)

$\[ {\mathbf{A}}_{cp}=\left[\begin{array}{cc}0& 1\\ 0& 0\end{array}\right] \]$

(18b)

입자의 충돌이 발생할 때 주 시스템과 입자의 속도가 변하는 것을 반영하기 위하여 연속 시간 상태 방정식에서 이산 시간 상태 공간 방정식을 유도하였다. 주 시스템의 이산 시간 상태 공간 방정식은 다음과 같이 쓸 수 있다.

$\[ {\mathbf{z}}_{s\left(k+1\right)}={\mathbf{A}}_{ds}{\mathbf{z}}_{s\left(k\right)}+{\mathbf{B}}_{ds}{F}_{\left(k\right)} \]$

(19)

여기서 Δt는 표본추출주기이고,

$\[ {\mathbf{A}}_{ds}=e^{{\mathbf{A}}_{cs}\Delta t} \]$

(20a)

$\[ {\mathbf{B}}_{ds}=\left({\mathbf{A}}_{ds}-\mathbf{I}\right){{\mathbf{A}}_{cs}}^{-1}{\mathbf{B}}_{cs} \]$

(20b)

입자의 이산 시간 상태 공간 방정식은 다음과 같이 쓸 수 있다.

$\[ {\mathbf{z}}_{p\left(k+1\right)}={\mathbf{A}}_{dp}{\mathbf{z}}_{p\left(k\right)} \]$

(21)

여기서

$\[ {\mathbf{A}}_{dp}=e^{{\mathbf{A}}_{cp}\Delta t} \]$

(22)

위와 같이 시스템과 입자의 개수대로 각각의 이산 시간 상태 방정식을 정의해주고 초기 변위와 속도를 측정하여 대입하면 시간 변화가 반영된 변위와 속도를 계산할 수 있다. 계산된 각 물체의 변위를 이용하여 입자간 혹은 입자와 용기 내벽 간의 충돌이 발생하는지 식 (8)을 사용하여 알 수 있다. 충돌이 발생하지 않는다면, 앞서 계산된 변위와 속도는 다음 이산 시간 상태 방정식에 초기값으로 이용된다. 충돌이 발생된다면, 식 (11)을 사용하여 충돌 이후 각 물체의 속도를 새로이 계산하여 다음 계산식의 초기값으로 반영해준다.

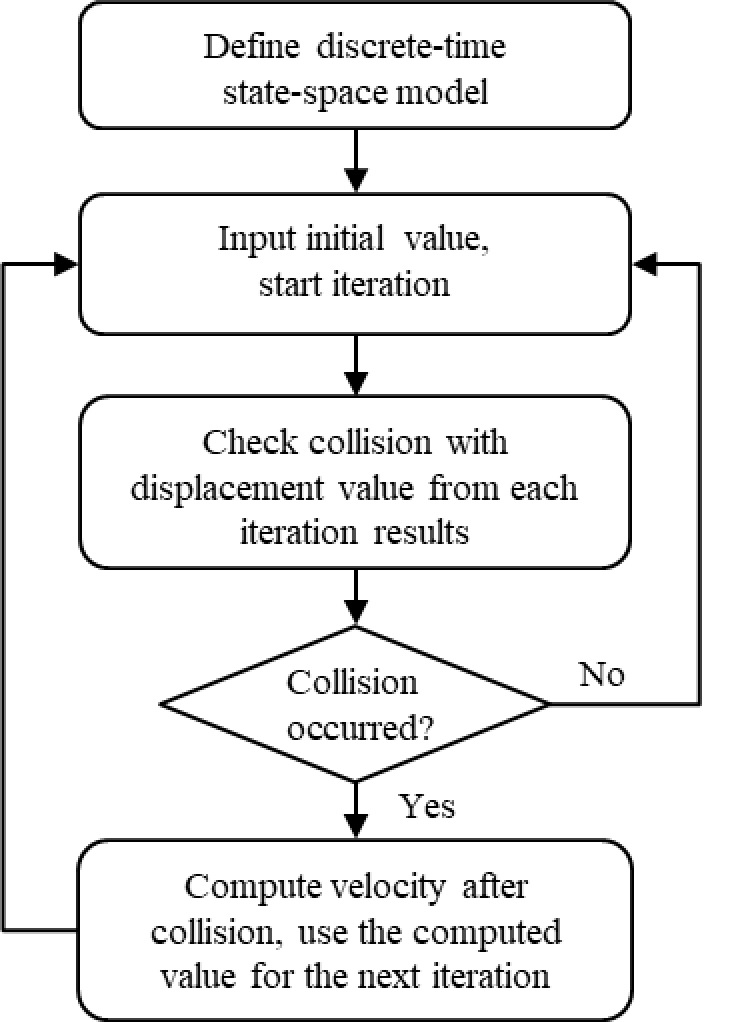
앞서 설명한 수치 계산 과정을 Fig. 2에 정리하였다. 위 과정을 반복하므로 충돌을 반영한 입자 충돌 댐퍼 시스템의 거동을 예측할 수 있다.

Fig. 2

Flow chart of numerical analysis

3. 자유진동 실험과 시뮬레이션 결과 비교

Fig. 3에 보이는 것과 같이 수평 운동을 하는 1자유도 알루미늄 구조물을 제작하고 윗부분에 볼베어링의 개수를 조절하여 담을 수 있는 플라스틱 용기를 부착하여 실험을 진행하였다. 입자를 제외하고 자유 진동 실험을 하여 시스템의 강성값과 감쇠 계수를 산출하였다. 이후 입자의 충돌실험을 진행하여 입자와 용기의 충돌 반발계수, e_s와 입자간의 반발계수, e_p를 측정하여 Table 1과 같은 값을 시뮬레이션 알고리즘에 반영하였다.

Fig. 3

PID system with three particles

Table 1

Parameters of the PID system

한 개부터 세 개까지 볼베어링 개수를 바꿔가며 시스템의 자유진동실험을 진행했다. 볼베어링의 개수가 많을수록 용기 내 입자 지름의 합을 제외한 빈공간(gap)의 거리는 짧아지며 그 길이는 Table 2와 같다.

Table 2

Length of gap by each system

실험을 진행하며 시스템과 입자의 초기 변위와 진동시 거동을 영상으로 기록하였고 영상내 물체의 변위를 측정할 수 있는 소프트웨어인 tracker⁽¹¹⁾를 이용하여 변위를 측정하였다. 입자가 움직일 때 미끄러짐 조건을 반영하지 않고 시스템과 입자의 변위를 시뮬레이션하여 실험 값과 비교하였다.

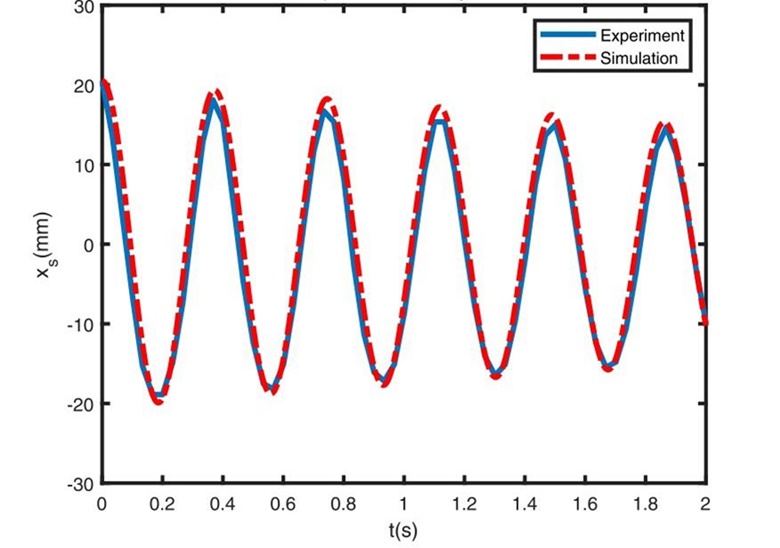
입자의 움직임을 제한하여 충돌 댐퍼가 작동하지 않을 때의 시스템의 변위를 측정하였고, 실험값과 시뮬레이션 값이 Fig. 4에서 나타나듯이 매우 유사한 것을 확인하였다.

Fig. 4

Displacement when particles are immovable

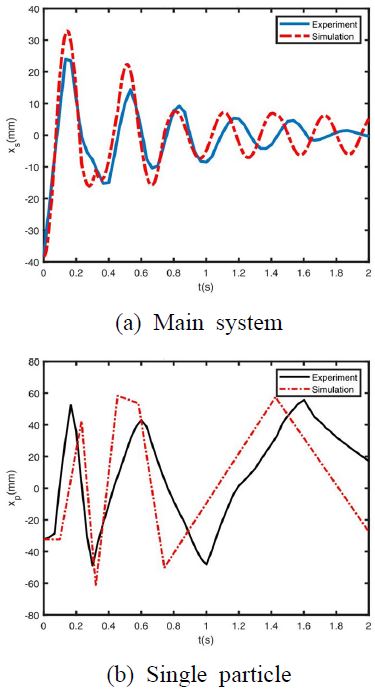
Fig. 5에 나타난 것과 같이 볼베어링 한 개를 이용한 입자 충돌 댐퍼 시스템의 자유 진동과 볼베어링의 변위를 측정하고 시뮬레이션한 것과 비교하였다. 시뮬레이션으로 나타난 시스템의 진동 감쇠와 입자의 움직임이 실험 결과와 유사한 것을 확인하였다.

Fig. 5

Displacements of the main system (a) and single particle (b)

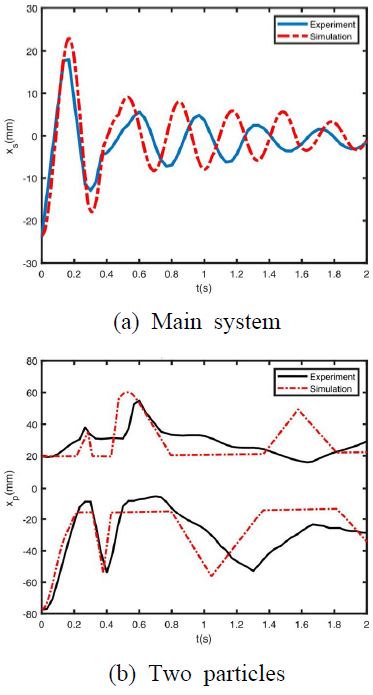
Fig. 6에 나타난 것과 같이 볼베어링 두 개를 이용한 입자 충돌 댐퍼 시스템의 자유 진동 실험에서도 시스템의 감쇠와 두 볼베어링이 충돌하기까지 변위가 시뮬레이션 결과와 유사한 것을 확인하였다.

Fig. 6

Displacements of the main system (a) and two particles (b)

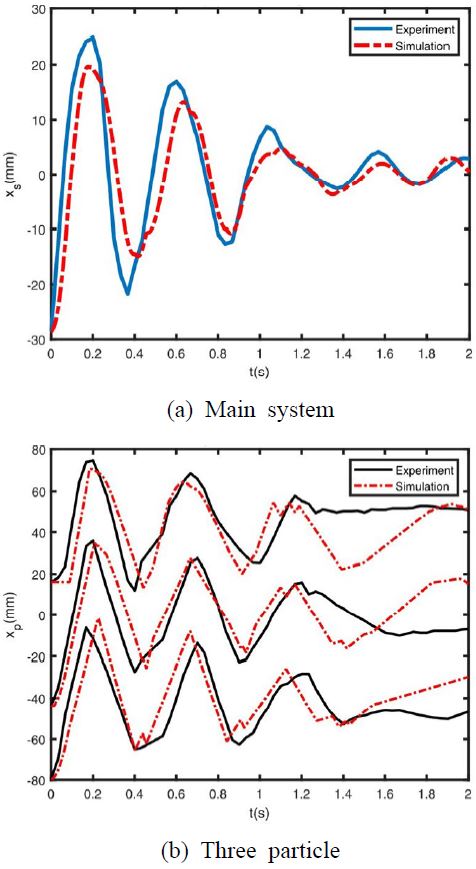
Fig. 7에 나타난 것과 같이 볼베어링 세 개를 이용한 입자 충돌 댐퍼 시스템의 자유 진동 실험에서도 시스템과 볼베어링의 거동이 시뮬레이션한 것과 유사하게 진동이 억제되는 것을 알 수 있다.

Fig. 7

Displacements of the main system (a) and three particles (b)

4. 결 론

이 연구에서 소개한 알고리즘은 다수의 입자가 일렬로 배열된 유형의 입자 충돌 댐퍼 시스템을 예측하는 알고리즘이다. 입자의 회전을 반영한 입자 충돌 댐퍼 시스템의 운동 방정식을 유도하고 입자와 시스템의 변위를 이용하여 충돌 발생 시점을 정의하였다. 충돌을 반영한 동적 해석을 수행하기 위하여 이산 시간 상태 공간 방정식을 활용하였다. 세 가지 유형의 입자 충돌 댐퍼 시스템에 대한 자유 진동 실험을 수행하고 시스템과 입자의 변위 값을 측정하여 시뮬레이션 데이터와 비교하였다. Figs. 5 ~ 7에서 알 수 있듯이 실험과 시뮬레이션 결과에서 전반적인 유사성을 확인하였다. 그러나 시뮬레이션으로 구현한 시스템의 진동이 다소 빠른것을 Fig. 5, Fig. 6에서 볼 수 있다. 이는 용기 바닥의 거칠기에 의한 미끄러짐 특성 조건을 반영하지 않았기 때문인 것으로 사료된다. Fig. 7에서 비교적 높은 유사도가 나타난것은 입자를 추가할수록 입자와 용기 사이의 빈 공간이 짧아지며 미끄러짐에 의한 영향이 상대적으로 적기 때문인것으로 이해할 수 있다.

여러 입자의 충돌에 의한 시스템의 비선형적인 거동을 시뮬레이션에 모두 반영하기에는 어려움이 있는것이 사실이다. 그렇기 때문에 이전의 입자 충돌 댐퍼 연구에서 대부분 동적 해석을 수행할 때 여러 입자를 하나의 입자로 변환하여 엄밀해를 정의하여 분석하거나 Runge-Kutta 방법을 적용하였다. 이 연구에서 소개한 수치 해석법은 이산 시간 상태 공간 방정식을 활용하여 주 시스템과 각 입자의 운동과 충돌을 상대적으로 간단하고 정확하게 시뮬레이션하고 시스템의 특성을 반영하여 직관적으로 해석할 수 있는 장점이 있다. 앞으로 입자 충돌 댐퍼 설계를 위한 활용이 가능할 것으로 판단된다.

Acknowledgments

이 연구는 2022년도 산업통상자원부 및 산업기술평가관리원(KEIT) 연구비 지원에 의한 연구임(‘20011159’).

References

• Lieber, P. and Jensen, D. P., 1945, An Acceleration Damper: Development, Design and Some Applications. Transactions of the American Society of Mechanical Engineers, Vol. 67, pp. 523~530. [https://doi.org/10.1115/1.4018316]
• Masri, S. F. and Caughey, T. K., 1966, On the Stability of the Impact Damper. Journal of Applied Mechanics, Vol. 33, pp. 586~592. [https://doi.org/10.1115/1.3625125]
• Masri, S. F. and Ibrahim A. M., 1973, Response of the Impact Damper to Stationary Random Excitation, Journal of the Acoustical Society of America, Vol. 53, No. 1, pp. 200~211. [https://doi.org/10.1121/1.1913319]
• Bapat, C. and Sankar, S., 1985, Single Unit Impact Dampers in Free and Forced Vibration, Journal of Sound and Vibration, Vol. 99, No. 1, pp. 85~94. [https://doi.org/10.1016/0022-460X(85)90446-8]
• Papalou, A. and Masri, S. F., 1996, Response of Impact Dampers with Granular Materials under Random Excitation, Earthquake Engineering and Structural Dynamics, Vol. 25, No. 3, pp. 253~267. [https://doi.org/10.1002/(SICI)1096-9845(199603)25:3<253::AID-EQE553>3.0.CO;2-4]
• Papalou, A. and Masri, S. F., 1996, Performance of Particle Dampers Under Random Excitation, Journal of Vibration and Acoustics, Vol. 118, No. 4, pp. 614~621. [https://doi.org/10.1115/1.2888343]
• Papalou, A. and Masri, S. F., 1998, An Experimental Investigation of Particle Dampers under Harmonic Excitation, Journal of Vibration and Control, Vol. 4, pp. 361~379. [https://doi.org/10.1177/107754639800400402]
• Friend, R. D. and Kinra, V. K., 2000, Particle Impact Damping, Journal of Sound and Vibration, Vol. 233, No. 1, pp. 93~118. [https://doi.org/10.1006/jsvi.1999.2795]
• Yang, W., Ahn, S., Koh, H. and Park, J., 2014, Study on a Reduction of Railway Vibration using Impact Dampers, Proceedings of the KSNVE Annual Autumn Conference, pp. 119~120.
• Lu, Z., Lu, X., Jiang, H. and Masri, S. F., 2014, Discrete Element Method Simulation and Experimental Validation of Particle Damper System, Engineering Computations, Vol. 31, No. 4, pp. 810~823. [https://doi.org/10.1108/EC-08-2012-0191]
• Tracker, https://physlets.org/tracker, (accessed Jan 5, 2023).