중형기동 회전익기 진동 하중 감소를 위한 선형 개별 블레이드 제어 법칙 설계 및 시뮬레이션

1. 서 론

회전익 항공기는 로터 시스템으로 인하여 기동 시 진동 및 소음을 수반한다. 로터의 진동 하중을 수동 또는 능동적으로 억제하는 연구들이 수행되어 온 가운데 능동형 기법으로는 동체 장착형 작동기, 회전익 항공기의 로터에서 발생하는 진동 하중을 발생원인 로터 회전축에서 제어하는 기법인 higher harmonic control (HHC) 기법과 개별 블레이드를 조절하는 individual blade control (IBC) 방법이 설계 및 실험을 통하여 연구되어 왔다^(1~6). HHC 및 IBC 기법은 개별 블레이드를 N/rev, N±1/rev의 구동 주파수로 제어하여 공기력을 섭동시켜 진동을 억제한다. 기존 HHC 및 IBC기법은 식 (1)과 같이 로터의 민감도를 전달행렬(transfer matrix) [T]의 형태로 모델링하고, 이를 적응형 제어 기법 등을 이용하여 진동 지수를 최소화하는 알고리즘을 구성하는 것이 일반적이다.

이러한 제어 기법은 통합 로터 해석 및 실험에 의해 진동 하중의 충분한 감소 능력을 보였으나, 제어기 시뮬레이션과 폐루프 실험 결과와의 비교 검증 등의 체계적인 설계 절차가 거의 제시되지 않았다. 또한, 전달 행렬 접근법은 로터의 동특성을 간단한 대수 관계로 공식화하기 때문에 안정성 및 강인성에 대한 평가 항목이 결여되어 있다. 따라서, HHC 및 IBC 제어기 설계에도 ADS-33⁽⁷⁾에 의거한 선형 안정성 분석이 요구된다.

이 논문에서는 저자⁽⁸⁾에 의하여 제시된 바 있는 선형 시불변 관계의 시스템 식별이 가능하도록 하는 N/rev, (N±1)/rev의 IBC 제어 입력을 이용하여 중형 회전익기 로터 특성을 갖는 BO-105 축소 시험로터 HART-II 및 UH-60A 실규모 로터 형상에 적용한 진동 제어 시뮬레이션 및 상대 안정도 판별 결과를 소개한다.

2. 본 론

2.1 로터 시스템 모델링 방법

(1) HART-II 로터

로터시스템 해석을 위해 국부 좌표계 기반의 변분 회전을 도입하여 전산해석을 단순화시킨 혼합 변분법 기하학적 정밀 보 구조 해석과 헬리콥터 로터 동적 해석을 위한 Peters-He가 제시한 동적 유입류 및 ONERA-EDLIN 동적 실속 모델을 결합한 로터 연계 해석 프로그램을 개발하여 적용하였다.

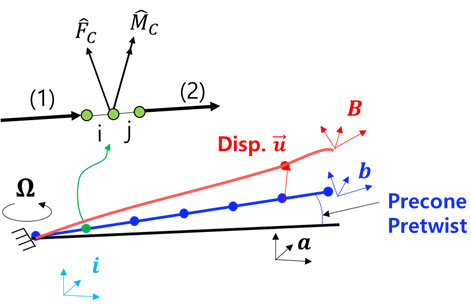
로터 시스템의 보 해석을 구성하기 위하여 Fig. 1과 같은 좌표계를 구성하여 좌표계 변환 행렬을 정의할 수 있다. Fig. 1에서 i는 고정 허브좌표계, a는 회전 허브좌표계, b는 보의 변형 전 초기 형상이 정의된 좌표계, 그리고 B는 변형 후 좌표계이다. 혼합변분법으로 정의된 보 지배방정식에서 경계조건 구성을 통해 회전 조인트 등의 다물체 요소 확장이 용이하다. 이 논문에서는 무힌지형 로터 블레이드를 모사하기 위하여 회전 조인트 및 베어링의 감쇠 및 스프링 계수를 적용하였다.

Fig. 1

Present beam frame definition

Peters의 비정상 양력선 이론은 B-좌표계를 기준으로 정의되며, 식 (3)과 같이 좌표계 변환을 통해 자유류 속도와 유입류 속도가 정의된다. 유입류는 Peters-He의 3차원 동적 유입류를 적용하였다.

$\[ \overrightarrow{U_B}=C^{Ba}\left(C^{ai}{V}_{\infty }+\lambda \overrightarrow{e_3}-C^{aB}{V}_B\right) \]$

(3)

회전 변환 행렬(3×3)은 Euler 각 Φ 및 지수맵 회전 정식화를 이용하여 식 (4)와 같이 정의되며, 모든 물리량은 회전 허브 전역(material) 좌표계에서 정의된다.

$\[ C=e^{\tilde{\mathrm{\varphi }}}=I+\frac{\sin {\theta }_a}{{\theta }_a}\tilde{\mathrm{\varphi }}+\frac{1-\mathrm{c}\mathrm{o}\mathrm{s}{\theta }_a}{{\theta }_a^2}{\tilde{\mathrm{\varphi }}}^2 \]$

(4)

Peters 비정상 양력선 이론은 정적 공기력을 풍동시험이나 CFD 계산을 통해 구한 정적 공기력 계수 C81표를 참조하여 계산하며, 정적 항력 계수를 이용한 표면 점성 항력 보정을 수행한다. 비정상 공기력은 식 (5)와 같이 계산한다.

$\[ \begin{array}{c}{L}^{us}=a_0\rho \frac{c^2}{4}\left(U_2{\omega }_1-\frac{{\dot{V}}_{B3}}{2}\right)\\ D^{us}=0\\ M^{us}=-a_0\rho \frac{c^4}{256}{\dot{\omega }}_{B1}-\frac{c}{4}{L}^{us}\end{array} \]$

(5)

ONERA-EDLIN 동적 실속은 식 (6)와 같이 동적 실속 추가 계수를 정적 공력 계수에 더하여 계산한다. 식 (7)에서 양력, 항력 및 모멘트 방향으로 각각 상태변수 형태의 미분방정식을 통해 동적 실속 추가 계수를 획득한다. 식 (6)에서 f_rev는 후퇴면 역흐름에 대한 변수이며, 익형 상대속도에 따라 0 또는 1의 값을 가진다.

$\[ \begin{array}{c}{L}^{ds}=\frac{\rho c}{2}\sqrt{U_1^2+U_2^2}{\Gamma }_L\\ D^{ds}=\frac{\rho c}{2}\sqrt{U_1^2+U_2^2}{\Gamma }_D\\ M^{ds}=\frac{\rho c^2}{2}\sqrt{U_1^2+U_2^2}{\Gamma }_M+c{L}^{ds}\frac{f_{rev}-1}{4}\end{array} \]$

(6)

$\[ \begin{array}{l}\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]=\left[\begin{array}{cc}0& 1\\ -{\omega }^2& -\eta \end{array}\right]\left[\begin{array}{c}{x}_1\\ x_2\end{array}\right]+\left[\begin{array}{c}0\\ 1\end{array}\right]\left\{-{\omega }^2\left(\Delta C+e\Delta C\right)\right\}\\ C_L=c_l-\left(c_{l0}+c_{l\alpha }\mathrm{s}\mathrm{i}\mathrm{n}\alpha \right)\\ \Delta C_D=c_d-c_{d0}+c_{d\alpha }{\mathrm{s}\mathrm{i}\mathrm{n}}^2\alpha \\ C_M=c_m-\left(c_{m0}+c_{m\alpha }\mathrm{s}\mathrm{i}\mathrm{n}\alpha \right)\end{array} \]$

(7)

코드 구성은 Eigen3 C++ 라이브러리를 이용하여 밀집 행렬 연산을 수행하고 Intel MKL PARDISO를 이용하여 희박행렬 계산을 수행하였다.

(2) UH-60A 로터

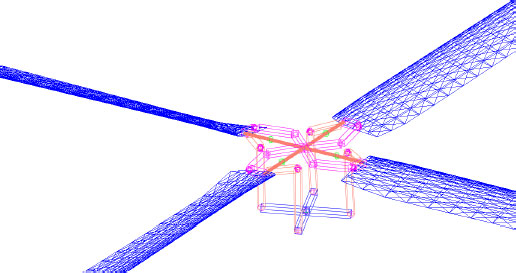
UH-60A의 해석에는 플랩, 래그, 비틀림 방향의 조인트, 래그 감쇠기 및 스워시 플레이트 등 다물체 구조를 모두 구성하였으며, 다물체 동역학 해석 프로그램 DYMORE 2.0을 활용하였다. DYMORE 2.0에 포함된 기능인 Peters-He 동적 유입류 및 양력선 이론을 사용하여 공기력을 계산하였다. 모델링 된 로터는 Fig. 2에 나타내었다. 이 연구의 해석 대상인 HART-II 로터와 UH-60A 로터의 제원을 Table 1에 정리하였다.

Fig. 2

DYMORE2.0 UH-60A modeling

Table 1

Main rotor properties of HART-II and UH-60A

2.2 로터 선형 고조화 진동 제어기 설계 기법

(1) 제어 변수 및 입출력 신호 정의

임의의 로터에 대하여 회전좌표계에서의 개별 블레이드 조종값을 식 (8)과 같이 선정하면 다중블레이드좌표계 회전변환 관계에 의해 비회전좌표계에서 N/rev의 출력만을 얻을 수 있음을 알 수 있다⁽⁸⁾. 괄호안의 지수는 블레이드 번호, 괄호 없는 지수는 N/rev, (N±1)/rev 주파수를 나타내며 각각 cosine 및 sine의 기저 함수로 구분할 수 있다. 식 (8)에서 블레이드 간 위상차가 없는 콜렉티브 조종 값은 N/rev 주파수를 그대로 전달하며, ±2π(i-1)/N, (i=1,2,3,…N)의 위상을 가지는 조종값은 (N±1)/rev의 주파수를 N/rev으로 각각 전달한다. 이러한 제어 입력에 대하여 고정좌표계에서의 허브 하중 변화량 또한 cosine 및 sine의 기저 함수로 나타내면 식 (9)와 같이 나타낼 수 있다.

$\[ \begin{array}{c}{\theta }^i={\theta }_c^{N}cosN\psi +{\theta }_s^{N}sinN\psi \\ +{\theta }_c^{N+1}cos\left\{(N+1)\psi +\frac{2\pi (i-1)}{N}\right\}\\ +{\theta }_s^{N+1}sin\left\{(N+1)\psi +\frac{2\pi (i-1)}{N}\right\}\\ +{\theta }_c^{N-1}cos\left\{(N-1)\psi +\frac{2\pi (i-1)}{N}\right\}\\ +{\theta }_s^{N-1}sin\left\{(N-1)\psi +\frac{2\pi (i-1)}{N}\right\}\end{array} \]$

(8)

$\[ \begin{array}{c}{F}_{z,N}-F_{z0,N}=\delta F_{zc}^{N}cosN\psi +\delta F_{zs}^{N}sinN\psi \\ M_{x,N}-M_{x0,N}=\delta M_{xc}^{N}cosN\psi +\delta M_{xs}^{N}sinN\psi \\ M_{y,N}-M_{y0,N}=\delta M_{yc}^{N}cosN\psi +\delta M_{ys}^{N}sinN\psi \end{array} \]$

(9)

(2) 로터 선형 시스템 모델링 및 식별 방법

전달함수 식별을 위하여 식 (8)의 각 기저 함수의 크기 성분을 로터의 동적해석 수행시 충분한 회전이 이루어진 정상상태에서 τ_threshold 시간 이후에 계단 입력으로 부여한다.

(10)

허브 하중 변화량의 N/rev 성분의 하중을 추출하기 위하여 N/rev 주파수에 해당하는 신호의 극값들을 추출하여 계단 응답에 대한 전달함수 추정을 수행하였다. 식 (11)과 같이 허브 수직전단 하중과 롤링, 피칭 모멘트에 해당하는 6개 성분만을 사용하여 전달함수는 6개 입력 벡터 성분 $$ {\left[{\theta }_c^N,{\theta }_s^N,{\theta }_c^{N+1},{\theta }_s^{N+1},{\theta }_c^{N-1},{\theta }_s^{N-1}\right]}^T$$과 6개 출력 하중 $$ {\left[\delta F_{zc}^N,\delta F_{zs}^N,\delta M_{xc}^N,\delta M_{xs}^N,\delta M_{yc}^N,\delta M_{ys}^N\right]}^T$$으로 구성하였다. 각 입력성분에 해당하는 SISO 전달함수는 zero를 포함하는 6차/6차 형태로 모델링이 가능하다. 전달함수를 대각행렬로 정의하고 이를 상태공간 방정식으로 변환하여 LTI 시스템 행렬 A, B, C, D를 획득할 수 있다.

$\[ \begin{array}{cc}\delta y=\left[\begin{array}{c}\delta F_{zc}^N\\ \delta F_{zs}^N\\ \delta M_{xc}^N\\ \delta M_{xs}^N\\ \delta M_{yc}^N\\ \delta M_{ys}^N\end{array}\right],& \delta u=\left[\begin{array}{c}{\theta }_c^N\\ {\theta }_s^N\\ {\theta }_c^{N+1}\\ {\theta }_s\\ {\theta }_c^{N-1}\\ {\theta }_s^{N-1}\end{array}\right]\end{array} \]$

$\[ \delta y=\left[\begin{array}{cccccc}\frac{\delta F_{zc}^N}{{\theta }_c^N}& & & & & \\ & \frac{\delta F_{zs}^N}{{\theta }_s^N} & & & & \\ & & \frac{\delta M_{xc}^V}{{\theta }_c^{N+1}}& & & \\ & & & \frac{\delta M_{xs}^N}{{\theta }_s^{N+1}}& & \\ & & & & \frac{\delta M_{yc}^N}{{\theta }_c^{N-1}}& \\ & & & & & \frac{\delta M_{ys}^N}{{\theta }_s^{N-1}}\end{array}\right]\delta u \]$

$\[ \left\{\begin{array}{l}\dot{x}=\left[A\right]x+\left[B\right]\delta u\\ \delta y=\left[C\right]x+\left[D\right]\delta u\end{array}\right. \]$

(11)

(3) 진동 하중 제어기 설계

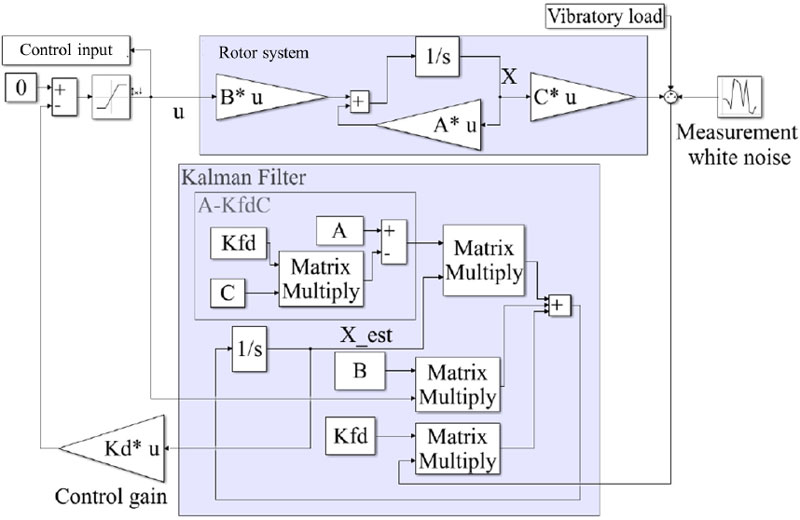
식별된 선형 시스템 행렬 A, B, C, D를 이용하여 LQG(Linear quadratic Gaussian) 제어 구조를 적용하면 계측되는 N/rev 로터 진동 하중에 대해 N/rev 섭동 하중을 발생시켜 로터 진동을 제어할 수 있다.

Fig. 3은 로터 진동을 감소시키기 위한 블록선도를 나타낸다. MATLAB/Simulink 환경에서 시뮬레이션을 수행하여 정적 게인을 획득하고 이를 해석 프로그램에 적용하여 제어 해석을 수행하였다. 상태변수의 관측기는 정상상태 칼만 필터를 적용하였다. 관측기 이득은 트림 해석결과의 $$ {\left[F_{zc}^N,\delta F_{zs}^N,M_{xc}^N,M_{xs}^N,M_{yc}^N,M_{ys}^N\right]}^T$$의 N/rev 하중성분의 크기를 대각행렬 R_k의 구성성분으로 하고, 대각행렬 Q_k의 크기를 반복적으로 관측기의 성능을 만족하도록 구할 수 있다. 제어 이득을 획득하기 위하여 식 (12)와 같은 출력 궤환 방식의 목적함수를 이용하여 Q와 R을 선정하였다. 식 (12)에서 HL_i는 i-방향의 허브 진동 하중이며 |u_max|는 IBC 제어 입력 최대 크기이다. α_i, β_i및 ρ는 이 연구에서는 최적화를 수행하지 않았으며 휴리스틱 방법으로 결정하였다.

Fig. 3

LQG control diagram for the present IBC system

$\[ \begin{array}{c}J=\frac{1}{2}{\int }_0^{\infty } x^T{C}^{T}QCx+u^{T}Rudt\\ Q=diag\left(\left[\frac{{\alpha }_{ic}}{{\left\{\mathrm{m}\mathrm{a}\mathrm{x}\left({HL}_{ic}\right)\right\}}^2}\frac{{\alpha }_{is}}{{\left\{\mathrm{m}\mathrm{a}\mathrm{x}\left(H{L}_{is}\right)\right\}}^2}\right]\right)\\ R=\frac{\rho }{{\left|u_{\mathrm{m}\mathrm{a}\mathrm{x}}\right|}^2}diag\left(\left[{\beta }_{ic}{\beta }_{is}\right]\right)\end{array} \]$

(12)

2.3 시뮬레이션 결과

(1) HART-II 로터 기본 해석 결과

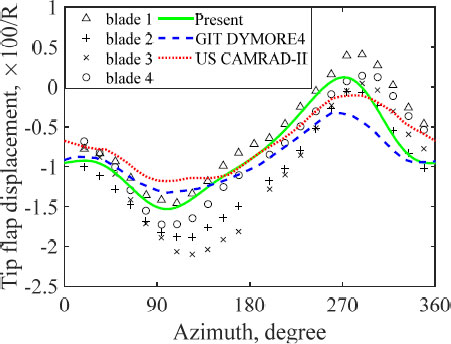
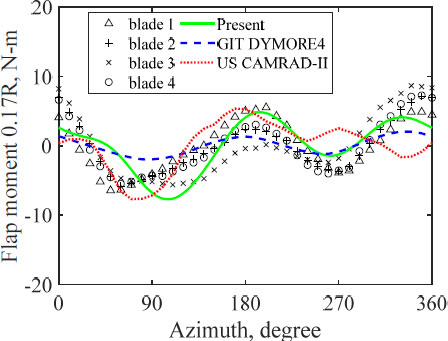
Fig. 4는⁽⁹⁾ HART-II의 5.3° 하강비행 조건(baseline)에서 로터 블레이드의 끝단 변형 크기를 나타내며, Fig. 5는⁽⁹⁾ 블레이드의 뿌리로부터 17 % 지점에서 플랩 방향 굽힘 모멘트를 나타낸다. 개발된 해석 프로그램이 시험 결과와 유사하며, 동일한 수준의 보 이론 및 공기역학 이론을 사용한 기존 로터 통합 해석 프로그램과 비교하여 유사한 수준에서 예측하고 있음을 발견하여 개발된 해석 프로그램의 유효성을 확인하였다⁽⁹⁾.

Fig. 4

Tip flap-wise displacement of the baseline HART II

Fig. 5

Flap-wise bending moment at 0.17R of the baseline HART II

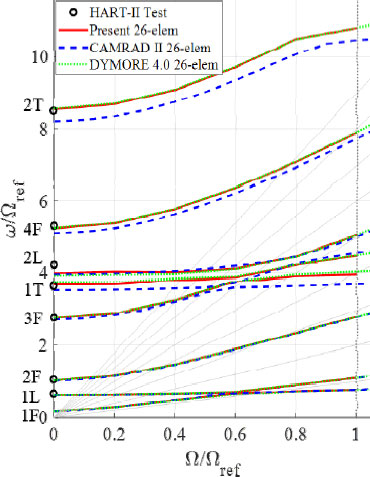
Fig. 6은⁽⁹⁾ HART-II 로터의 회전속도에 따른 모드 해석 결과를 나타낸다. 상용 해석 프로그램과 유사한 예측 성능을 보이고 있으며, 동일한 요소 개수에서 요소간 물성 보간에 선형 보간을 사용하는 CAMRAD-II, DYMORE 4.0 보다 더 실험 결과에 가까운 예측 결과를 보였다.

Fig. 6

HART II fan plot

(2) UH-60A 로터 기본 해석 결과

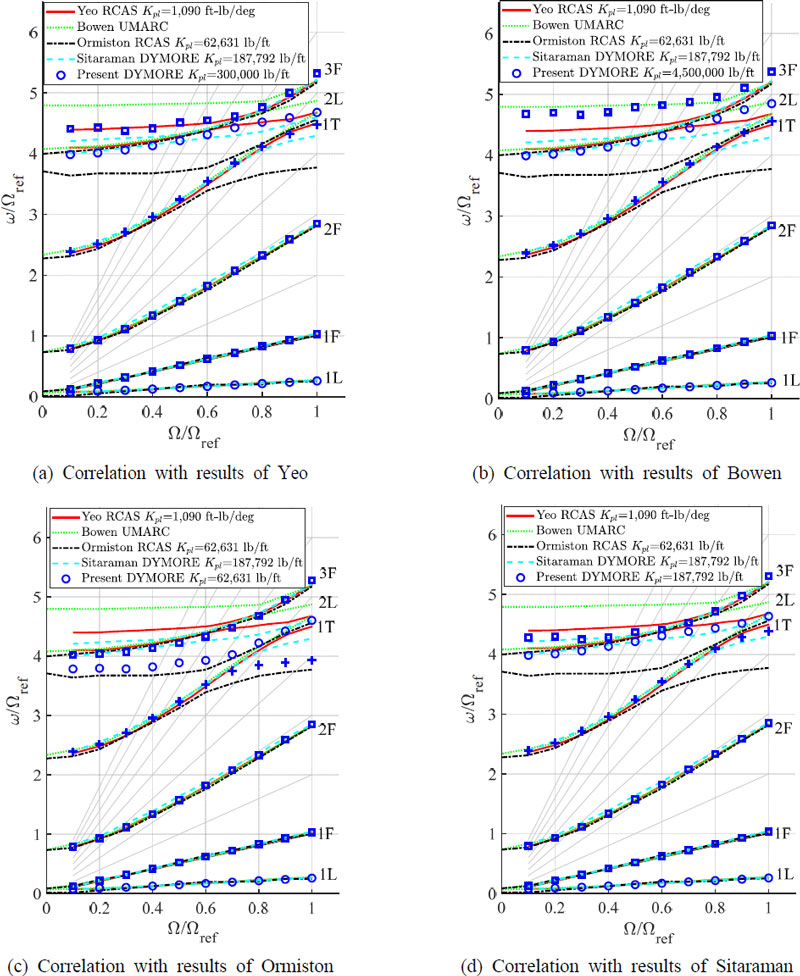
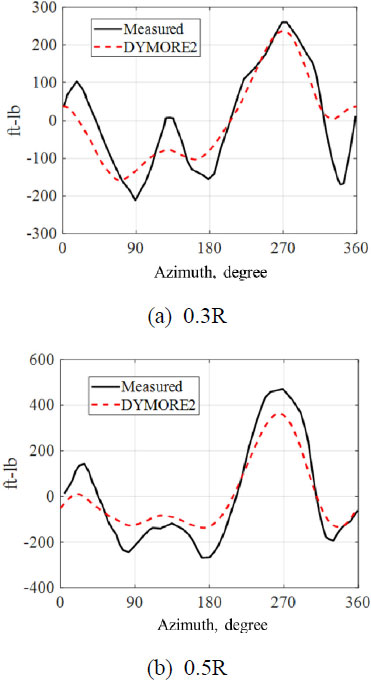
UH-60A 로터는 비행 시험 결과의 C8513 조건에서 해석을 수행하였다. 이는 전진비 0.15, 로터 디스크 하중 계수 0.08 및 0.76° 하강비행 조건으로 HART-II의 해석 조건과 유사하다. Fig. 7 (a) ~ (d)에서 이 연구에서 구성된 UH-60A 로터의 피치링크 강성을 조절함에 따라 참고문헌들의 결과를 재생산할 수 있음을 보이며, Fig. 8 (a), (b)는 블레이드 30 % 지점과 50 % 지점에서 트림 수행후 플랩 방향 굽힘 모멘트를 나타낸다^(10~13). 따라서 현재 사용된 DYMORE 2.0 해석파일이 올바르게 구성되었음을 관측하였다.

Fig. 7

UH-60A fan plot

Fig. 8

Flap-wise bending moment of the baseline UH-60A

(3) 로터 LTI 시스템 식별 결과

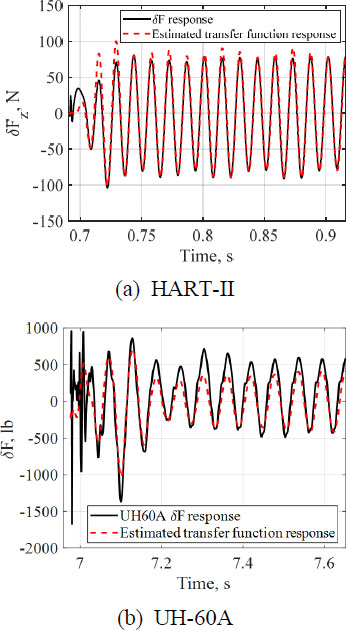
Fig. 9 (a)와 (b)에 HART-II 로터와 UH-60A 로터에 대해 도출된 전달함수 결과 일부를 도시하였다. N/rev 주파수 성분의 과도응답의 특성이 적절히 모사되었음을 확인할 수 있고, 1.5/rev 이하의 주파수 동특성 범위를 가진다.

Fig. 9

Transfer function identification results

(4) 진동하중 제어 해석 결과

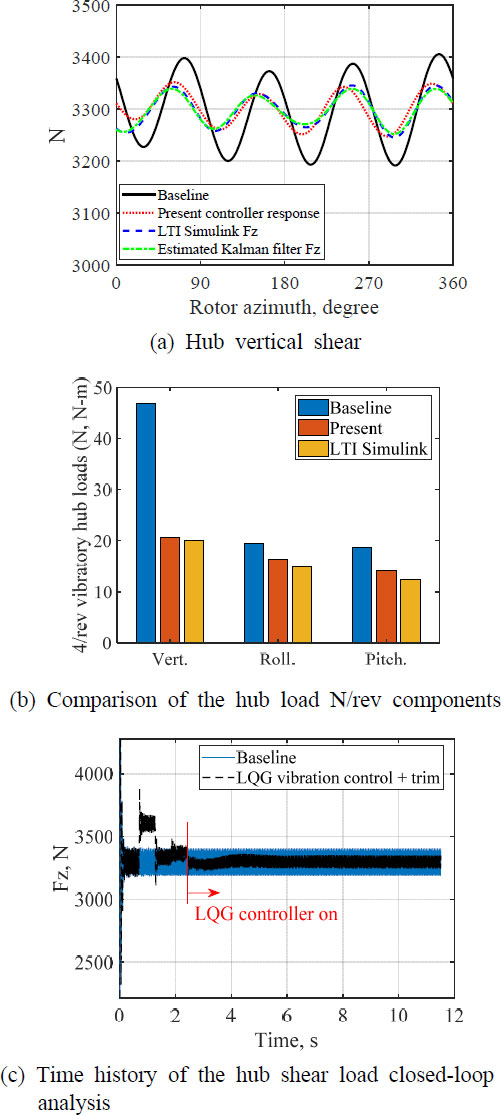
Fig. 10은 HART-II 로터의 제어 해석 결과를 나타낸다. 로터의 트림 해석과 진동하중 제어기가 코드 내에서 동시에 작동하도록 하였으며, LQG 제어기가 작동하기 이전에 하중의 변화 구간은 로터 트림을 위한 콜렉티브 및 사이클릭 피치의 민감도 행렬을 식별하는 구간이다. LQG 제어기 작동시 추력이 일부 감소하나 트림제어기의 작동으로 트림상태로 복귀함을 보이며, 트림 제어기가 작동할 경우에도 평균 50 %의 진동하중 감소 성능을 보였다.

Fig. 10

HART-II vibratory load control results

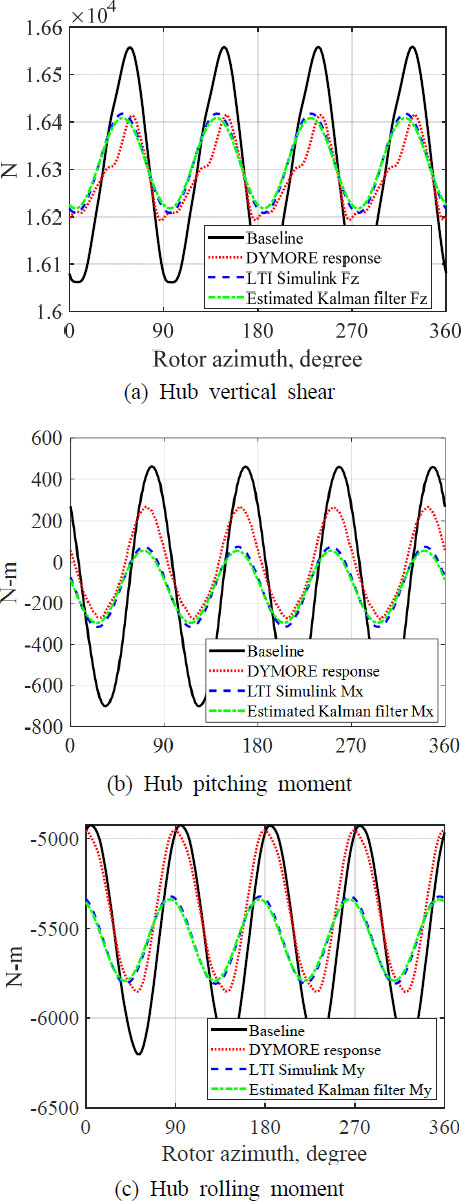
Fig. 11은 UH-60A의 진동하중 제어 예측 응답을 도시하고 있다. DYMORE2.0을 활용하여 MATLAB/Simulink 선형 시스템에서 도출된 제어 입력을 개루프 방식으로 인가하는 방식으로 해석을 수행하였다. 롤링, 피칭 모멘트 방향의 모델링 오차가 다소 존재함을 관측하였다.

Fig. 11

UH-60A vibratory load control results

선형 모델링된 시스템에서 예측한 성능과 비선형 시뮬레이션에 적용된 제어기의 응답 예측이 유사한 수준임을 확인하였으며, 선형시스템의 위상 및 이득 여유가 적절히 설계될 수 있음을 의미한다. MATLAB/Simulink의 루프 절단 방법을 통해 개루프 시스템 전달함수를 얻어 다중 입출력 시스템에 대한 상대 안정도를 디스크(disk) 여유 계산을 이용하여 해석하였다. 계산된 각 로터의 최소 여유값은 Table 2에 요약하였다.

Table 2

Gain and phase margin

3. 결 론

이 논문에서는 개별 피치 제어 기법을 이용한 중형기동 회전익기 특성을 갖는 HART-II 로터와 UH-60A의 다물체 동역학 모델링이 수행되었으며, 개별 고조화 피치 제어 입출력 신호 정의 방법 및 선형 시스템 모델링 방법을 소개하였다. 다물체 동역학 해석에 LQG 제어 알고리즘을 적용하여 진동하중 제어시스템을 구성할 수 있었으며, 그 결과는 선형 시스템의 해석 결과와 유사하였다. 이를 통해 로터 진동하중 감소 제어기 설계를 위해 설계자의 의도대로 진동하중제어 성능과 상대 안정도를 결정할 수 있으며, 향후 제약조건을 적용한 최적화 알고리즘의 적용을 통해 제어기 이득 상수를 적절하게 모델링할 수 있을 것으로 기대된다.

Acknowledgments

이 논문은 2019년도 정부(미래창조과학부)의 재원으로 한국연구재단의 지원을 받아 수행된 연구임(No. 2017R1A2B4004105). 이 연구는 서울대학교 차세대 우주추진 연구센터와 연계된 미래창조과학부의 재원으로 한국연구재단의 지원을 받아 수행한 선도연구센터지원 사업(NRF-2013R1A5A1073861)의 연구 결과입니다.

References

• Shin, S. J., Cesnik, C. E. S. and Hall, S. R., 2005, Closed-loop Control Test of NASA/ARMY/MIT Active Twist Rotor for Vibration Reduction, Journal of the American Helicopter Society, Vol. 50, No. 2, pp. 178~194. [https://doi.org/10.4050/1.3092854]
• Roget, B. and Chopra, I., 2010, Closed-loop Test of a Rotor with Individually Controlled Trailing-edge Flaps for Vibration Reduction, Journal of the American Helicopter Society, Vol. 55, No. 1, pp. 1~10. [https://doi.org/10.4050/JAHS.55.012009]
• Straub, F. K., Anand, V. R., Birchette, T. S. and Lau, B. H., 2009, SMART Rotor Development and Wind Tunnel Test, 35th European Rotorcraft Forum.
• Lee, Y., Kim, D., Park, J. and Hong, S., 2019, Airframe Vibration Reduction Simulation using Active Rotor Control and Active Vibration Control System for High-speed Compound Rotorcrafts, Proceedings of the KSNVE Annual Autumn Conference, p. 166.
• Hong, S. and Park, J., 2021, Active Vibration Control Test of High-speed Compound Unmanned Rotorcraft using Scaled Airframe Model, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 31, No. 6, pp. 642~653. [https://doi.org/10.5050/KSNVE.2021.31.6.642]
• U.S. Army Aviation and Missile Command, 2000, Handling Qualities Requirements for Military Rotorcraft, Aeronautical Design Standard-33.
• Im, B. U., Lee, C. B., Kee, Y. J. and Shin, S. J., 2021, Investigation of Linear Higher Harmonic Control Algorithm for Rotorcraft Vibration Reduction, Journal of Dynamic Systems, Measurement, and Control, Vol. 143, No. 1, pp. 011008(1~12). [https://doi.org/10.1115/1.4048369]
• Smith, M. J., Lim, J. W., van der Wall, B. G., Baeder, J. D., Biedron, R. T., Boyd, D. D., Jayaraman, B., Jung, S. N. and Min, B.-Y., 2012, An Assessment of CFD/CSD Prediction State-of-the-Art Using the HART II International Workshop Data, 68th Annual Forum of the AHS.
• Ormiston, R. A., 2004, An Investigation of the Mechanical Airloads Problem for Evaluating Rotor Blade Structural Dynamics Analysis, American Helicopter Society 4th Decennial Specialists’ Conference on Aeromechanics.
• Bowen-Davies, G. M., 2015, Performance and Loads of Variable Tip Speed Rotorcraft at High Advance Ratios, Ph.D. Thesis, University of Maryland, College Park.
• Yeo, H. and Potsdam, M., 2016, Rotor Structural Loads Analysis Using Coupled Computational Fluid Dynamics/Computational Structural Dynamics, Journal of Aircraft, Vol. 53, No. 1, pp. 87~105. [https://doi.org/10.2514/1.C033194]
• Sitaraman, J. and Roget, B., 2009, Prediction of Maneuver Loads Using a Fluid-structure Analysis, Journal of Aircraft, Vol. 46, No. 5, pp. 1770~1784. [https://doi.org/10.2514/1.43004]