폭발 하중을 받는 그래핀 나노판 보강 다공 코어 샌드위치판의 과도 응답
© The Korean Society for Noise and Vibration Engineering
Abstract
This paper presents the transient response analysis conducted for sandwich plates subjected to blast load. These plates are made of two isotropic face sheets and a porous core composed of closed-cell foam. The core with functionally graded pore distribution through the thickness direction is uniformly reinforced using graphene nanoplatelets. Three different porosity distributions are considered, namely, two functionally graded symmetric types and a uniform type. In the analytical method of investigating the transient response of sandwich plates, Reddy’s third order shear deformation theory is employed. To verify the reliability of the presented analytical method, the transient responses are compared to those obtained using the ANSYS software. The influences of the weight fraction, geometry of the graphene nanoplatelet, porosity distribution and porosity coefficient on the transient response are examined using a few examples.
Keywords:
Transient Response, Graphene Nanoplatelet, GNP Reinforced Composite, Porous Core, Sandwich Plate키워드:
과도 응답, 그래핀 나노판, GNP 보강 복합재료, 다공성 코어, 샌드위치 판1. 서 론
금속 폼은 샌드위치 구조의 코어로 사용할 경우 무게를 줄일 수 있다는 장점때문에 많은 관심을 받고 있다. 그러나 다공성 재료에서 기공의 존재는 구조의 강성을 감소시킬 수 있기 때문에 경량을 유지하면서 강성이 감소되는 것을 방지하는 것은 매우 중요하다. 탄소 나노 튜브에 비해 넓은 표면적을 갖는 그래핀 나노판(graphene nanoplatelet, GNP)은 고분자 및 금속 복합재료의 보강재로 사용할 경우 우수한 보강 효과를 얻을 수 있으며, 기저재료에 소량의 GNP 등과 같은 나노 필러로 보강을 하면 기계적 성능을 향상시킬 수 있다(1). 또한 GNP는 넓은 표면적뿐만 아니라 고강도, 저밀도인 특성을 가지고 있어 다공성 재료의 보강재로 사용될 수 있다. 이와 같이 GNP로 보강된 다공성 재료를 샌드위치 구조의 코어로 사용함으로써 무게 증가없이 강성을 증가시킬 수 있어 경량 스마트 구조물에 적용할 수 있다.
GNP 보강 다공성 경사 기능 구조에 대해 많은 연구가 진행되고 있다. Kitipornchai 등은(2) GNP 보강 다공성 보에 대해 진동 및 좌굴 해석을 하였다. Zhou 등(3)은 초음속 유동을 받는 원통형 패널에 대해 진동 및 플러터 특성을 연구하였다. Ansari 등(4)은 여러 형상의 판에 대한 후좌굴 및 진동 특성을 제시하였다. 또한 GNP 보강 다공성 재료를 코어로 하는 샌드위치 구조에 대해서도 연구가 진행되고 있다. Yaghoobi 등(5)은 샌드위치 판에 대해 좌굴 해석을, Twinkle 등(6)은 원통형 샌드위치 패널에 대해 좌굴 및 진동 특성을 연구하였다. Kim(7)은 샌드위치 판의 진동 특성을 분석하였다. 특히 최근 들어 폭발에 의한 다양한 종류의 우발적 또는 의도적 사건 등이 발생되고 있다. 폭발에 대한 구조물의 안전을 확보하기 위해 많은 연구가 진행되고 있다. Liu 등(8)은 탄성 경계조건을 갖고 탄성 지지된 GNP 보강 다공성 판에 대해 동적 해석을 수행하였다. Zhao 등(9)은 형상기억합금선이 내제된 샌드위치 쉘 구조물에 대해 동적 해석을 하였다.
이상에서와 같이 GNP 보강 다공성 코어를 갖는 샌드위치 구조에 대해 일부 연구가 이루어졌으나 그 양은 제한적이며, 특히 폭발 하중에 대한 거동 분석은 매우 미미하다. 따라서 이 연구에서는 폭발 하중을 받는 GNP 보강 다공성 코어를 갖는 샌드위치판에 대한 과도 응답에 대해 연구하였다. 샌드위치판과 같은 두꺼운 판에 대해 고전 이론이나 1차 전단변형이론을 적용하여 횡전단 변형 특성을 얻기 위해서는 3차원 평형 방정식을 추가로 적용하여야 한다. 그러나 고차 전단변형이론을 적용할 경우 추가 작업없이 횡 전단 변형 특성을 얻을 수 있기 때문에 이 해석에서는 Reddy의 3차 전단변형이론을 적용하였다. 폭발 하중을 받는 GNP 보강 다공성 코어를 갖는 샌드위치판의 과도응답특성을 구하기 위해 변분 원리를 적용하여 운동방정식을 유도하였다. 제안된 해석적 방법의 타당성을 검증하기 위해 ANSYS를 이용한 유한요소해석을 수행하여 그 결과를 비교/검토하였다. 또한 GNP의 무게비 및 형상비, 기공의 양 및 기공의 두께 방향 분포 형태 등이 과도 응답 특성에 미치는 영향을 분석하였다.
2. GNP 보강 다공성 코어 샌드위치판의 수식화
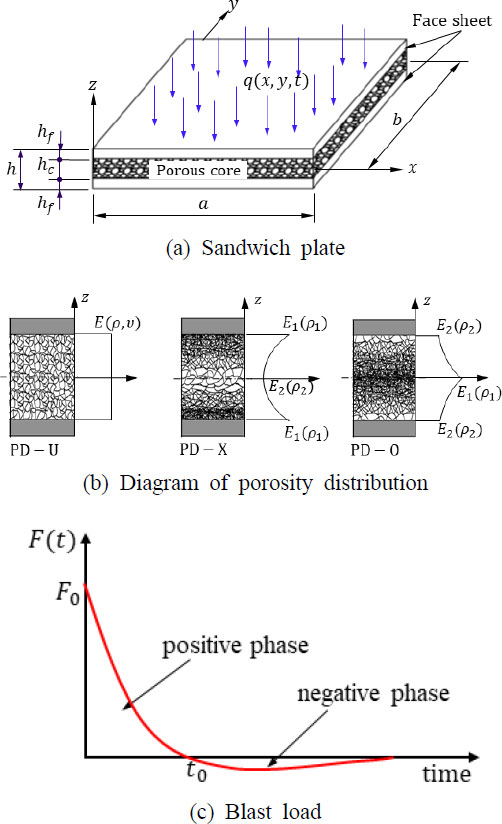
이 연구에서는 폭발 하중을 받는 GNP 보강 다공성 코어를 갖는 샌드위치 사각판을 고려하였다. Fig. 1(a)에서 a, b 및 h는 판의 길이, 폭 및 두께를, hc와 hf는 코어 및 외피의 두께이다. GNP보강 코어는 기공이 두께 방향으로 연속적으로 변화하도록 두께가 매우 얇은 층으로 적층된 복합재료로 취급하였다. 코어의 각 층 두께는 동일하며, 각층에서의 기공은 균일하게 분포된다고 가정하였다. 또한 각층에 대해 GNP는 모든 방향에 대해 균일하게 분포되며, 무작위로 위치하게 된다. 따라서 각 층의 중앙면에서의 물성을 그 층의 재료물성으로 취급할 수 있다.
수정된 Halpin-Tsai 모델에 따라 기공이 없는 GNP 보강 복합재료의 유효 탄성계수(E1), 푸아송 비(ν1) 및 밀도(ρ1)는 다음과 같다(1,2).
| (1) |
| (2) |
| (3) |
여기서 ηL, ξL및 ηT, ξT는 GNP의 기하계수로 다음과 같다.
| (4) |
| (5) |
식에서 Em, vm, ρm은 기저 재료의, EG, vG, ρG는 GNP의 탄성계수, 푸아송 비 및 밀도이다. 또한 aG, bG 및 tG은 GNP의 길이, 폭 및 두께이다. VG는 기공이 없는 코어의 GNP 부피 비로 다음과 같다.
| (6) |
여기서 wG은 GNP의 무게 비이다.
코어의 기공은 각 층의 중앙면을 따라 두께 방향으로 다음과 같이 함수적으로 변한다고 가정하였다.
| (7) |
두께방향으로의 기공 분포 유형은 기공 분포가 균일한 것 (PD-U)과 중앙면을 기준으로 대칭 분포된 것 (PD-X, PD-O) 등으로 총 3가지를 고려하였다(2). 여기서 PD-X는 중앙면을 기준으로 외면으로 갈수록 기공이 작아지며, PD-O는 기공이 커지는 특징을 갖는다(Fig. 1(b)). 이에 따라 코어의 재료물성은 PD-U의 경우 두께 방향을 따라 일정하며, PD-X는 재료가 바깥쪽에 많이 존재하여 바깥쪽의 물성이 최대가 되며, 중앙면에서 최소가 된다. 반대로 PD-O는 중앙면에서 최대, 바깥쪽에서 최소가 된다.
이 연구에서는 폐쇄형 쉘 폼을 코어로 고려하였다. 폐쇄형 쉘 폼의 재료물성은 다음과 같다(10).
PD-U에 대한 분포함수 α는
| (8) |
| (9) |
여기서 e0은 다공성 계수이다. Mt는 코어의 총 질량으로 모든 기공 분포에 대해 동일하다.
| (10) |
ρe는 다공성 재료의 유효 밀도이다.
| (11) |
| (12) |
여기서 em(z)은 질량 밀도 계수이다.
다공성 재료의 유효 탄성계수는 식 (13)과 같다.
| (13) |
한편 유효 푸아송 비는 두께 방향에 따라 다음과 같이 변한다(11).
| (14) |
샌드위치판에 대한 해석에서 횡 전단변형과 회전 관성을 고려하기 위해 Reddy의 3차 전단변형이론으로부터 변위장(u, v 및 w는 x, y 및 z 방향 변위)을 다음과 같이 쓸 수 있다(12).
| (15) |
여기서 u0, v0 및 w0는 중립면에서 x, y, z 방향 변위를, ϕx, ϕy 는 y 및 x 축에 대한 회전을 나타낸다. 식에서 (,)는 다음에 나타나는 첨자에 대한 미분을 의미하며, c1 = 4/(3ℎ2)이다.
사각판의 어느 한 점의 변형률은 내평면 변형률(ϵxx, ϵyy, γxy) 및 횡전단 변형률(γyz, γzx)로 구성된다.
| (16) |
k-번째 층의 응력(σ)과 변형률(ϵ) 관계는
| (17) |
이다. Q(k)는 k-번째 층의 축약 강성도 행렬이다.
이 연구에서는 판의 각 변에서 다음 조건을 갖는 단순 지지된 경계조건을 고려하였다.
| (18) |
경계조건을 만족하는 판의 중립면에 대한 변위식을 다음과 같이 표현할 수 있다.
| (19) |
식에서 Umn, Vmn, Wmn, Xmn, Ymn는 고유 모드, αm = mπ/a, βn = nπ/b 이고, m, n은 모드 수, ηmn(t)는 모드 기여도 인자이다.
하중을 받는 샌드위치판에 저장되는 총 에너지는 다음과 같다.
| (20) |
여기서 U는 샌드위치판의 변형에너지, T는 운동에너지이며, W는 판의 표면에 수직으로 작용하는 하중 q(x,y,t)에 의해 행해진 일로 각각 다음과 같다.
| (21) |
| (22) |
| (23) |
식에서 NL은 적층수이며, 수직 하중은 짧은 시간 동안 판 전체에 균일하게 작용하며 다음과 같은 급수 형태로 표현할 수 있다.
| (24) |
시간에 대한 함수 fmn(t)를 다음과 같이 Duhamel적분형태로 표현할 수 있다.
| (25) |
여기서 wmn은 고유진동수이며, 짧은 시간 동안 작용하는 폭발 하중은 다음과 같다(Fig. 1c).
| (26) |
여기서 F0는 하중 최대 크기, a0는 파장 감소계수이며, t0는 양의 하중이 작용하는 시간으로 이 시간 이후에는 매우 작은 음의 하중이 작용한다.
동하중에 대한 구조물의 응답을 구하기 위해 식 (20)에 Rayleigh-Ritz 정리에 적용한 후 변분을 취하면 다음과 같은 운동방정식을 얻을 수 있다.
| (27) |
여기서 K, M은 강성 및 질량행렬이며, Q는 하중벡터, d는 모달 행렬이다.
식 (27)은 다음과 같이 간단히 정리할 수 있다.
| (28) |
식 (28)의 해는 다음과 같다.
| (29) |
이 결과 식을 각 방향 변위식 (19)에 대입하면 구하고자 하는 응답을 얻을 수 있다.
3. 수치 결과 및 토의
이 연구에서 고려한 샌드위치판의 외피는 구리, 코어는 구리를 GNP로 보강한 경사 기능 적층 복합재료이다. 사용된 재료의 물성 및 기하형상에 대한 자료를 Table 1에 제시하였다(2). 결과로 제시된 판의 고유진동수 ω, 중앙점에서의 수직변위 w, 수직응력 σx 및 횡전단응력 τzx을 다음과 같이 무차원화하여 수치결과를 제시하였다.
| (30) |
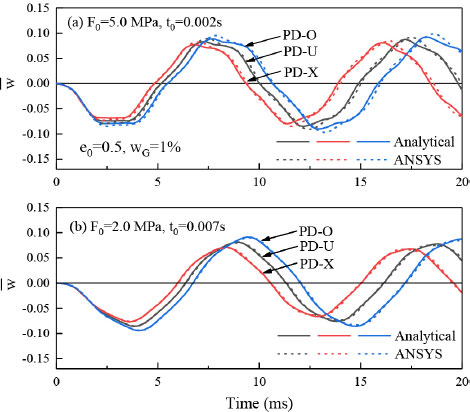
과도응답에 대한 제안된 해석방법의 타당성을 검증하기 위해 ANSYS를 이용하여 유한요소해석을 수행하였다. 유한요소해석에서 모델을 단순화하기 위해 적층 복합재료로 모델링하였으며, SHELL281 요소가 이용되었다. 하중조건으로 a0 = 2이며, F0 = 2.0Mpa, t0 = 0.007s와 F0 = 5.0Mpa, t0 = 0.002s 두 경우의 과도응답에 대한 유한요소해와 함께 해석해를 Fig. 2에 제시하였다. 또한 해의 응답특성을 예측하기 위해 무차원 고유진동수가 Table 2에 제시되었다. Table 2 및 Fig. 2에 나타난 것처럼 모든 기공 분포에 대해 유한요소해 및 해석해가 매우 잘 일치하는 것을 볼 수 있다.
PD-X의 경우 판의 중앙면으로부터 멀수록 재료가 많이(기공은 적게) 분포하게 되어 굽힘강성이 PD-U 분포보다 증가하게 되어 진동수도 PD-U보다 증가하게 된다. 반대로 PD-O는 중앙면에 재료가 집중되어 굽힘강성이 감소하여 진동수도 감소하게 된다(Table 2). Fig. 2에서 기공분포 형태에 따라 최대 처짐은 PD-X 기공분포를 갖는 판이 가장 작게, PD-O에서 가장 크게 발생된다. 이는 식 (29)를 통해 진동수가 클수록 처짐이 작아진다는 것을 알 수 있다. 특히 기본 진동수(1차 진동수)에 의해 가장 큰 영향을 받는다. 또한 응답 주기도 기본진동수가 클수록 작아지는 것을 볼 수 있다. 이처럼 과도 응답의 특징은 기본진동수의 크기에 의해 결정되는 것을 확인할 수 있다.
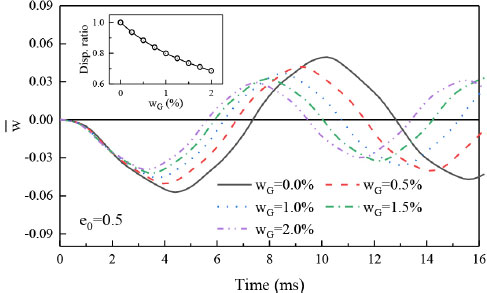
GNP의 무게비 wG가 과도응답에 미치는 영향을 Fig. 3에 제시하였다. 앞으로 제시되는 모든 수치 예에 F0 = 1.0Mpa, t0 = 0.001s, a0 = 2의 하중 조건이 이용된다. 그림에서처럼 GNP양이 증가함에 따라 응답 주기가 짧아지고, 최대 처짐도 감소한다. GNP 무게비 증가는 판의 강성을 증가시키며, 이에 따라 진동수 증가의 원인이 된다. 진동수 증가는 과도 응답의 진동 주기를 짧게 하고, 처짐을 감소시킨다. GNP보강판의 최대 처짐을 비보강판의 최대처짐으로 나눈 처짐 비를 작은 그래프로 나타냈다. 그림에서 1.0 %의 GNP만을 보강하여도 최대처짐이 20 % 정도 감소하는 것을 확인할 수 있다. 이처럼 적은 양의 GNP를 사용하여도 처짐을 크게 줄일 수 있다.
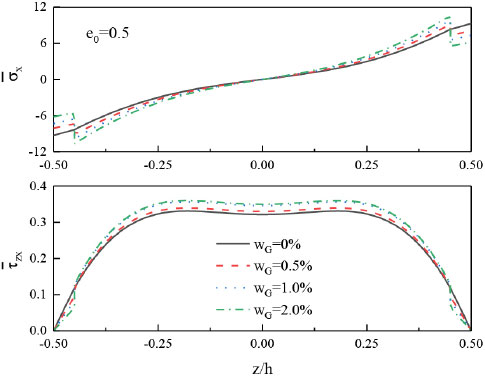
한편 Fig. 4에서는 PD-X분포를 갖는 판에 대해 wG가 응력에 미치는 영향을 알아보았다. wG의 증가에 따라 코어에서의 수직응력()은 증가하지만 외피에서는 감소하는 것을 볼 수 있다. wG가 증가함에 따라 코어에서는 유효탄성계수가 중앙면에서 멀어질수록 증가하게 되어 응력이 커진다. 그러나 금속재로만 구성된 외피에서는 굽힘에 의한 처짐이 wG가 증가함에 따라 작아지기 때문에 수직응력은 감소한다. 횡전단응력()의 경우 wG가 증가할 수록 코어에서의 응력은 증가하지만 수직응력에 비해 매우 작기 때문에 그 영향은 매우 적다고 할 수 있다. 1.0 %의 GNP로 보강할 경우 코어에서의 최대수직응력은 약 11 % 증가하지만, 외피에서는 21 %의 응력 감소가 일어난다. 횡전단응력의 경우 코어에서의 최대 응력은 약 8 % 증가를 한다. 이처럼 소량의 GNP를 사용하여 코어를 보강할 경우 처짐감소뿐만 아니라 응력감소 효과도 얻을 수 있다.
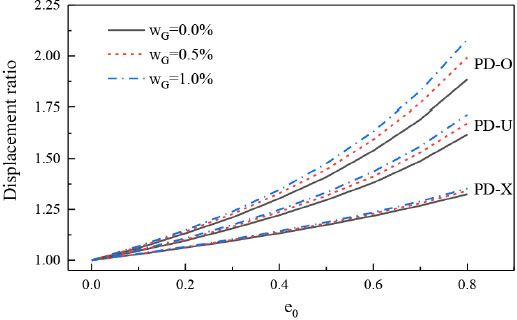
Fig. 5에서는 다공성 계수 e0가 최대처짐에 미치는 영향을 나타냈다. 그림에서 처짐 비는 다공성 판의 최대처짐을 기공이 없는 판의 최대처짐으로 나눈 값으로 e0가 증가할수록 코어의 강성 저하로 인해 처짐이 증가를 한다. 특히 같은 e0에 대해 wG가 클수록 최대처짐이 증가를 한다. 이는 wG가 클수록 기공의 영향이 커진다는 것을 의미한다. 또한 기공 증가에 의한 판의 강성 감소가 wG가 클수록 크다는 것을 의미한다. e0의 영향이 PD-O에서 가장 크게 작용을 하며, PD-X분포가 가장 작게 작용을 한다.
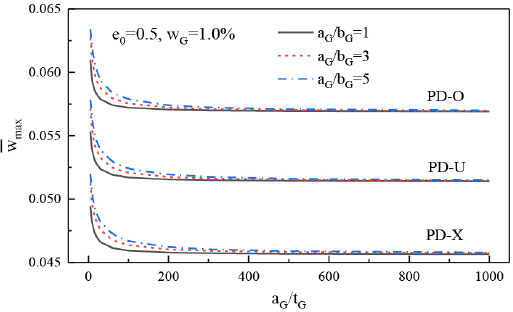
Fig. 6은 GNP의 길이 대 두께 비(aG/tG)가 최대 처짐에 미치는 영향을 보여준다. 여기서 GNP의 두께 tG는 일정하다. 기공 분포 형태에 관계없이 GNP의 aG/tG가 커질수록(GNP의 길이가 길어질수록, 또는 기저재료와의 접촉면적이 커질수록) 최대 처짐이 초기에 급격히 감소하다가 어느 값(500) 이상이 되면 거의 일정해진다. 또한 GNP의 형상비(aG/bG)가 작을수록(GNP가 정사각형일 경우 직사각형보다 기저재료와의 접촉면적이 큼) 처짐은 작아지며, aG/bG 비가 클수록 aG/tG의 영향이 커져 최대처짐이 급격히 감소를 한다. 그리고 aG/tG의 영향은 기공분포형태에 관계없이 거의 유사하다.
4. 결 론
이 연구에서는 폭발 하중을 받는 그래핀 나노판으로 보강된 다공성 코어를 갖는 샌드위치판의 과도응답 특성에 대해 연구하였다. 해석을 통해 다음과 같은 결론을 얻었다.
(1) 같은 양의 재료를 이용하여 기공을 판의 중앙면 쪽으로 많이 분포 시킬 수록 처짐은 작아진다. 반대로 기공을 코어의 바깥쪽으로 많이 분포시킬수록 처짐은 증가한다.
(2) GNP의 양이 많아질수록 고유진동수가 증가하여 과도응답의 주기가 짧아지며, 최대 처짐은 크게 감소한다. 또한 수직응력도 크게 감소시킬 수 있다.
(3) 다공성 계수가 커질수록 최대 처짐은 증가하며, 무게비 wG가 클수록 기공의 영향은 증가한다. 또한 다공성 계수의 영향은 기공이 판의 중앙면쪽에 많이 분포될수록 증가한다.
(4) 같은 양의 GNP로 보강할 때 기저재료와의 접촉면적이 큰 GNP를 사용할 경우 접촉면적이 작은 GNP를 사용할 때보다 최대 처짐은 줄어든다.
Acknowledgments
이 논문은 전남대학교 학술연구비(과제번호: 2022-0140) 지원에 의하여 연구되었음.
References
-
Rafiee, M. A., Rafiee, J., Wang, Z., Song, H., Yu, Z. Z. and Koratkar, N., 2009, Enhanced Mechanical Properties of Nanocomposites at Low Graphene Content, ACS Nano, Vol. 3, No. 12, pp. 3884~3890.
[https://doi.org/10.1021/nn9010472]

-
Kitipornchai, S., Chen, D. and Yang, J., 2017, Free Vibration and Elastic Buckling of Functionally Graded Porous Beams Reinforced by Graphene Platelets, Materials and Design, Vol. 116, pp. 656~665.
[https://doi.org/10.1016/j.matdes.2016.12.061]

-
Zhou, X., Wang, Y. and Zhang, W., 2021, Vibration and Flutter Characteristics of GNP-reinforced Functionally Graded Porous Cylindrical Panels Subjected to Supersonic Flow, Acta Astronautica, Vol. 183, pp. 89~100.
[https://doi.org/10.1016/j.actaastro.2021.03.003]

-
Ansari, R., Hassani, R., Gholami, R. and Rouhi, H., 2021, Free Vibration Analysis of Postbuckled Arbitrary-shaped FG-GNP-reinforced Porous Nanocomposite Plates, Thin-walled Structures, Vol. 163, p. 107701.
[https://doi.org/10.1016/j.tws.2021.107701]

-
Yaghoobi, H. and Taheri, F., 2020, Analytical Solution and Statistical Analysis of Buckling Capacity of Sandwich Plates with Uniform and Non-uniform Porous Core Reinforced with Graphene Nanoplatelets, Composite Structures, Vol. 252, p. 112700.
[https://doi.org/10.1016/j.compstruct.2020.112700]

-
Twinkle, C. M. and Pitchaimani, J., 2022, Static Stability and Vibration Behavior of Graphene Platelets Reinforced Porous Sandwich Cylindrical Panel under Non-uniform Edge Loads using Semi-Analytical Approach, Composite Structures, Vol. 280, p. 114837.
[https://doi.org/10.1016/j.compstruct.2021.114837]

-
Kim, Y.-W., 2022, Vibration Characteristics of Sandwich Plates with Graphene Nanoplatelet Reinforced Porous Core, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 32, No. 6, pp. 580~587.
[https://doi.org/10.5050/KSNVE.2022.32.6.580]

-
Liu, J, Deng, X., Wang, Q., Zhong, R., Xiong, R. and Zhao, J., 2020, A Unified Modeling Method for Dynamic Analysis of GNP-reinforced FGP Plate Resting on Winkler-pasternak Foundation with Elastic Boundary Conditions, Composite Structures, Vol. 244, p. 112217.
[https://doi.org/10.1016/j.compstruct.2020.112217]

-
Zhao, J., Hu, J., Wang, T., Li, H., Guan, J., Liu, J. and Gao, Z., 2022, A Unified Modeling Method for Dynamic Analysis of GNPs-FGP Sandwich Shallow Shell Embedded SMA Wires with General Boundary Conditions under Hygrothermal Loading, Engineering Structures, Vol. 250, p. 113439.
[https://doi.org/10.1016/j.engstruct.2021.113439]

-
Roberts, A. P. and Garboczi, E. J., 2001, Elastic Moduli of Model Random Three-dimensional Closed-cell Cellular Solids, Acta Materialia, Vol. 49, No. 2, pp. 189~197.
[https://doi.org/10.1016/S1359-6454(00)00314-1]

-
Roberts, A. P. and Garboczi, E. J., 2002, Computation of the Linear Elastic Properties of Random Porous Materials with a Wide Variety of Microstructure, Proceedings of the Royal Society of London A: Mathematical, Physical and Engineering Sciences, Vol. 458, pp. 1033~1054.
[https://doi.org/10.1098/rspa.2001.0900]

-
Reddy, J. N., 1990, A General Non-linear Third-order Theory of Plates with Moderate Thickness, International Journal of Non-linear Mechanics, Vol. 25, No. 6, pp. 677~686.
[https://doi.org/10.1016/0020-7462(90)90006-U]


Young-Wann Kim received his Ph.D. degree from Chungnam National University in 1997. He is a professor of department of mechanical design engineering, Chonnam National University. His research interest includes the structural vibration & dynamics, and smart materials.