풍하중에 의한 경사진 송배전선의 진동 해석
© The Korean Society for Noise and Vibration Engineering
Abstract
This study focused on the vibrations of inclined transmission line subjected to wind load. The dynamic model of the inclined transmission line was derived using the assumed modes method (AMM). To this end, the kinetic and potential energies, as well as the virtual work by the wind load, were derived. Then, the equations of motion were derived using the Lagrange equation. Theoretical results indicate that wind load causes in-plane vibrations of higher frequency and out-of-plane deflection due to static load.
Keywords:
Transmission Line, Dynamic Modeling, Assumed-modes Method, Vortex Shedding키워드:
송전선, 동적 모델링, 가정 모드법, 와류 발산1. 서 론
송배전선에 바람이 작용하는 경우 필연적으로 송배전선에 진동이 발생한다. 만일 바람이 지속적으로 한 방향으로 일정하게 작용하는 경우, 와류에 의한 진동(vortex-induced vibrations)이 발생할 수 있고 out-of-plane 상으로는 정적 변위가 발생할 수 있다. 이 연구에서는 Fig. 1의 빨간색 원 안에 있는 배전선의 고유진동 특성과 풍하중이 작용할 때의 진동 특성을 조사하고 바람에 의한 진동 응답을 계산했다.
Fig. 1의 해당 부분은 6개의 전선으로 이루어져 있고 스페이스 댐퍼로 서로 간격을 유지하도록 되어 있다.
다른 송배전선과 달리 이 부분이 바람에 취약한 것으로 알려져 있는데, 경사진 단일 전선의 해석을 통해 진동시 어떤 위험이 발생할 수 있는지를 확인하고, 태풍과 같은 강풍이 불었을 경우 이로 인해 발생하는 진동 변위의 크기를 예측했다.
Irvine and Caughey(1)는 이도(sag)대 길이(span)의 비가 1:8 이하인 늘어진 균일 케이블의 자유진동 문제에 대한 선형 이론을 도입하였다. Irvine and Griffin(2)는 Irvine and Caughey(1)의 이론을 확장해 동적응답을 구하는 방법을 개발하였다. Henghold and Russel(3)은 비선형 유한요소법을 케이블 구조물에 적용하는 이론을 개발하였다. Henghold 등(4)은 3차원 공간상에서 케이블 자유진동 문제 유한요소법을 도입해 정식화 과정을 제시하였다. Irvine(5)는 이전의 연구(1,2)를 경사진 케이블의 자유진동에 적용할 수 있음을 보여주었다. Triantafyllou and Grinfogel(6)는 경사진 케이블에 대해 단순한 근사식을 유도할 수 있음을 보여주었다. Chang(7)은 케이블의 비선형 진동을 분석했는데 평면내 운동과 평면의 운동의 비선형 연성과 내부공진을 조사하였다. Desai and Punde(8)은 케이블로 지지되는 구조물의 동적해석을 위한 단순모델을 제시하였다. Zhou 등(9)은 케이블 코드(chord)와 평행한 중량성분을 고려해 경사진 케이블의 자유진동을 분석하였다.
이 연구에서 바람으로 인한 경사진 배전선의 진동 문제를 조사하였다. 그러나 실제 현장의 전선의 이도가 크지 않기 때문에 선형 범위내에서 해석이 진행되었다. 대신 중력에 의한 전선의 정적 처짐을 보정하였고 바람에 의한 진동 해석을 수행하였다. 전선의 변위는 가정 모드법을 적용하여 이산화하고 라그랑지 방정식을 이용해 운동방정식을 유도하였다. 유도한 운동방정식은 수치계산에 적합한 형태로 되어 있으며 이를 이용해 고유진동수, 고유진동모드, 바람에 의한 응답계산을 쉽게 수행할 수 있다.
2. 동적 모델
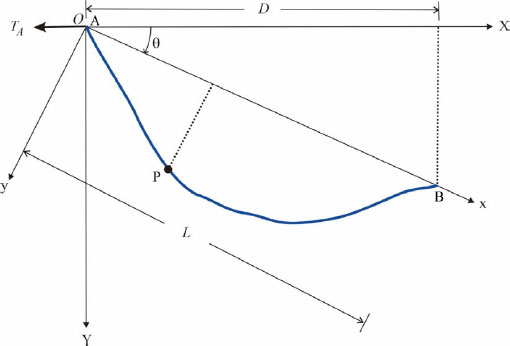
경사진 케이블의 동적 모델과 좌표계는 Fig. 2와 같다. 여기서 D는 케이블 양쪽 지지점 사이의 수평방향 거리, L은 A점과 B점을 연결하는 축의 간격을 나타내고, θ는 경사각, TA는 A점에서의 수평방향 장력을 나타낸다.
경사진 케이블의 xy축에 대한 정적 처짐의 고차 정밀해는 다음 식으로 주어진다(5).
| (1) |
여기서 ξ = x/L이며 이도율 δ는 다음 식으로 주어진다.
| (2) |
d는 케이블 중간에서의 y방향 처짐을 나타내고 m은 케이블의 전체 질량을 나타낸다. 그리고 섭동 파라미터(perturbation parameter)는 다음과 같다.
| (3) |
식 (1)로부터 경사는 다음식과 같이 유도된다.
| (4) |
여기서
| (5) |
중력으로 인해 케이블의 장력은 길이를 따라 변하게 되고 다음 식으로 표현된다.
| (6) |
여기서 은 케이블의 단위길이당 질량을 나타낸다. 그리고
| (7) |
주어진 모델에 대해 운동에너지와 위치에너지는 식 (8), (9)와 같이 표현된다.
| (8) |
| (9) |
u, v, w는 평형 위치로부터의 작은 동적 편차를 표현한다. u, v는 평면내(in-plane) 움직임의 수평 및 수직 성분을 나타내고, w는 평면외(out-of-plane) 움직임의 횡방향 수평 성분을 타나낸다. 여기서 변형률 ϵs은 다음 식으로 주어진다(8).
| (10) |
얕은 경사의 케이블(shallow catenary)이라고 가정하면, ds ≃ dx라고 표현 가능하다. 그러면 식 (10)을 다음과 같이 간략화할 수 있다.
| (11) |
ξ = x/L과 식 (4)를 식 (11)에 대입하면 다음과 같은 식이 유도된다.
| (12) |
식 (12)를 이용하고 고차항을 무시하면 식 (9)의 각 항을 다음과 같이 유도할 수 있다.
| (13) |
| (14) |
일반 좌표계와 허용함수를 도입하면 케이블의 변위들을 다음과 같이 표현할 수 있다.
| (15a) |
| (15b) |
| (15c) |
여기서 Φ(ξ) = [ϕ1(ξ)ϕ2(ξ) ⋯ ϕn(ξ)]는 허용함수 1 × n행렬이고,
qu(t) = [qu1(t)qu2(t) ⋯ qun(t)]T
qv(t) = [qv1(t)qv2(t) ⋯ qvn(t)]T
qw(t) = [qw1(t)qw2(t) ⋯ qwn(t)]T는 각 방향 변위에 대한 n × 1벡터이다. 그리고 n은 허용함수의 개수이다. 허용함수는 비교적 간단하게 다음과 같이 설정할 수 있다.
| (16) |
식 (15), (16)을 식 (8)에 대입하면 운동에너지는 다음과 같이 유도된다.
| (17) |
식 (13) ~ (16)을 식 (9)에 대입하면 위치에너지는 다음과 같이 유도된다.
| (18) |
여기서
| (19a) |
| (19b) |
| (19c) |
| (19d) |
| (19e) |
| (19f) |
| (19g) |
라그랑지 방정식을 이용하면 운동방정식이 다음과 같이 유도된다.
| (20) |
여기서 이고
| (21a) |
| (21b) |
| (22a) |
| (22b) |
여기서 In은 n × n단위행렬, 0n은 n × n영행렬, 0n1은 n × 1영벡터이다. 감쇠 행렬 Ct는 모달 감쇠행렬로부터 구하는 것으로 가정하였다. u방향으로의 외력은 작용하지 않는다고 가정하여 Qu = 0으로 설정하였다. 다른 일반화된 힘은 다음과 같이 표현된다.
| (22c,d) |
여기서 Fv와 Fw는 y축과 z축 방향으로 작용하는분산력이다. 식 (20)을 살펴보면 Qg라는 중력에 의한 정하중이 포함되어 있는 것을 알 수 있다. 그래서 q를 다음과 같이 설정할 수 있다.
| (23) |
여기서 qt는 시간에 따라 변하는 일반좌표계를 나타내며 qs는 정적처짐을 반영하는 일반좌표계를 나타낸다. 식 (23)을 식 (20)에 대입하면 다음과 같은 식이 유도된다.
| (24) |
| (25) |
식 (25)의 자유진동문제를 고려해보자.
| (26) |
식 (26)의 고유치문제를 풀면 다음과 같은 직교정상조건(orthonormal condition)을 만족하는 고유진동수 행렬과 고유진동모드 행렬이 얻어진다.
| (27) |
여기서 이다. 모달 감쇠를 가정할 경우 감쇠 행렬은 다음과 같은 식을 이용해 구할 수 있다.
| (28) |
여기서
Z = diag([ξ1 ξ2 ⋯ ξn])이고. Ω = diag([ω1ω2⋯ωn])이다. ζi(i = 1, 2,⋯n)는 각 모드에 대한 감쇠비이다. 행렬 운동방정식, 식 (25)로 주어지는 행렬 미분방정식을 이용해 응답을 계산하기 위해서는 상태방정식을 이용하는 것이 유리하다. 물론 모달 행렬을 이용해 축소모델(reduced-order Model)을 이용할 수도 있지만 이 연구에서는 모달 변환을 사용하지 않고 원래 식, 식 (25)를 그대로 이용하였다. 식 (25)에 대한 상태방정식은 다음과 같이 표현된다.
| (29a) |
| (29b) |
여기서 이고
| (30a) |
| (30b) |
| (30c,d) |
식 (29)의 상태방정식에 대해 바람에 의한 응답 계산을 위해 외력을 다음과 같이 가정하였다.
| (31a) |
| (31b) |
여기서 ρa는 공기의 질량 밀도, CL과 CD는 공기 흐름에 대한 양력 계수와 항력 계수이다. Vw는 바람의 속력, Aw는 공기력 계산을 위한 전단면적이다. ωe는 와류 발산(vortex shedding)에 의한 진동 주파수, 1 – e-0.75t항은 수치계산에 있어 점진적으로 힘이 강해질 수 있도록 만드는 부수적인 항이다. 식 (31a)를 식 (22a)의 Fv에 대입하고, 식 (31b)를 식 (22b)의 Fw에 대입하면 응답계산을 위한 일반력을 계산할 수 있다. 응답 계산을 수행하면 qt가 계산되고 정적 처짐을 추가하면 xy축에 대한 변위 u, v, w가 얻어진다. Fig. 2의 점 P를 고려해 원래 좌표계 Xp, Yp으로의 변환식은 다음과 같이 주어진다.
| (32) |
3. 수치계산
수치계산을 위한 케이블의 물성치는 Table 1과 같다.
공기와 바람에 관한 데이터는 Table 2와 같다.
Strouhal 상수를 이용하면 와류 발산 주파수(Vortex shedding frequency)가 24.6 Hz로 계산된다. 이는 케이블의 상당히 높은 고유진동 모드를 가진한다는 의미이며 따라서 진폭은 작게 나타날 것으로 예상할 수 있다.
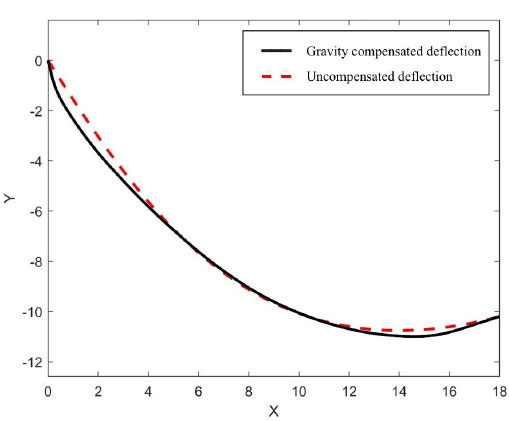
수치계산을 통해 x = L/2에서의 이도(sag)는 3.8 m로 계산되며, δ = 0.1847, ϵ = 0.3871가 계산된다. 식 (24)를 이용해 보상 정적 처짐을 계산한 결과가 Fig. 3과 같다. Fig. 3에서 빨간색 점선은 서로 다른 높이에서 양단이 지지되는 경사진 케이블을 나타내고, 검은색 실선은 중력에 의한 정적 처짐이 보상된 변위를 나타낸다.
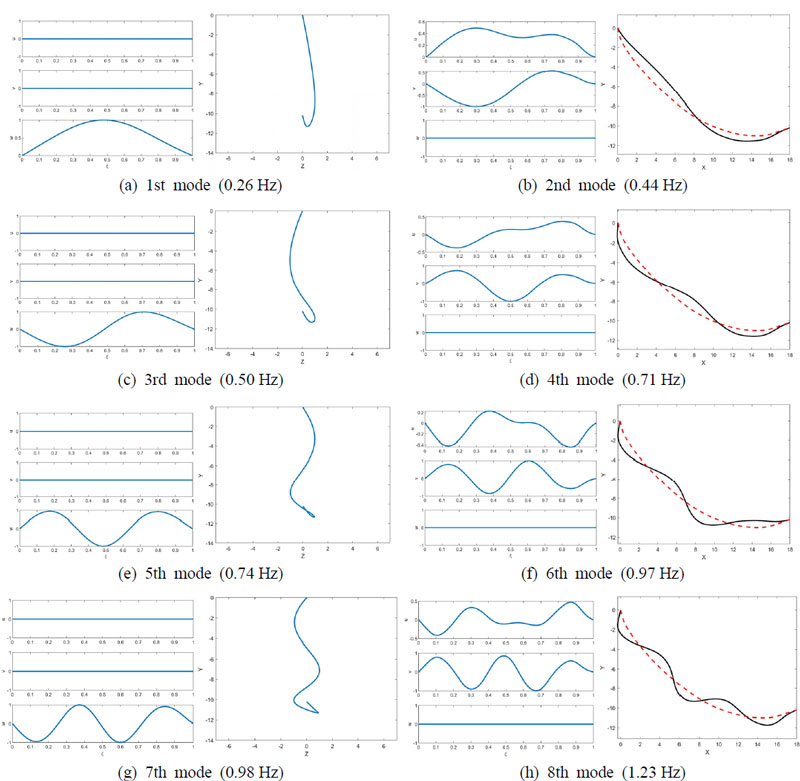
식 (26)을 이용해 비감쇠 고유진동수를 계산한 결과는 0.26 Hz, 0.44 Hz, 0.50 Hz, 0.71 Hz, 0.74 Hz, 0.97 Hz, 0.98 Hz, 1.23 Hz이고, 각 고유진동수에 대한 고유모드는 Fig. 4와 같다. Fig. 4(a), 4(c), 4(e), 4(g)는 평면 외 고유진동모드를 보여주고, Fig. 4(b), 4(d), 4(f), 4(h)는 평면 내 고유진동모드를 보여준다. 그래서 평면 외 진동과 평면 내 진동이 교차로 나타남을 알 수 있다.
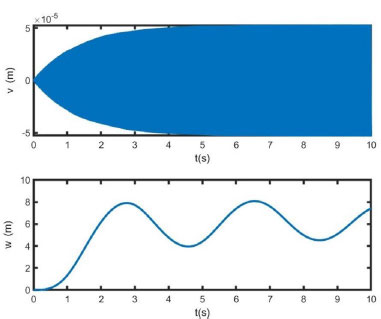
이론 계산 방법을 이용해 태풍이 불어올 때의 최대 변위를 계산해보면 Fig. 5와 같다. Fig. 5는 태풍의 속도를 50 m/s로 설정하여 시뮬레이션 프로그램을 실행했을 경우 발생하는 케이블 중간에서의 변위를 보여준다. 그림으로부터 와류에 의한 진동은 무시할 정도이나 태풍이 지속적으로 작용하는 경우 8 m가량의 큰 변위가 발생할 수 있음을 보여준다. 물론 풍하중에 의한 변위를 계산하고자 하는 경우 더 정확한 데이터가 필요하다. 이 연구에서는 최악의 시나리오를 가정하고 변위 계산을 수행했다.
4. 결 론
이 연구에서는 먼저 경사진 송배전선의 동적 모델을 유도하였다. 모델을 이용해 고유 진동특성을 파악하고 바람에 의한 진동응답을 예측하는 시뮬레이션을 수행하였다. 50 m/s의 강풍이 불 경우 평면 내(수직 방향) 진동은 거의 발생하지 않으나 평면 외(수평 방향) 방향으로는 약 8 m가량의 동적 변형이 일어날 수 있음을 알 수 있었다. 이 변형으로 인해 주위의 전선과 접촉할 수 있으며, 또한 과도한 정적 변형으로 인해 전선에 손상이 발생할 수 있다. 이 연구에서 개발한 경사진 송배전선의 동적 모델을 이용해 향후 송배전선의 안전성 예측을 수행할 수 있을 것으로 예상된다.
Acknowledgments
이 연구는 한국전력공사의 2022년 착수 사외공모 기초연구 사업에 의해 지원되었음(과제번호:R21XO01-42). 관계자 여러분께 감사드린다.
References
-
Irvine, H. M. and Caughey, T. K., 1974, The Linear Theory of Free Vibrations of a Suspended Cable, Proceedings of the Royal Society of London A: Mathematical and Physical Sciences, Vol. 341, No. 1626, pp. 299~315.
[https://doi.org/10.1098/rspa.1974.0189]

-
Irvine, H. and Griffin, J., 1976, On the Dynamic Response of a Suspended Cable, Earthquake Engineering & Structural Dynamics, Vol. 4, No. 4, pp. 389~402.
[https://doi.org/10.1002/eqe.4290040406]

-
Henohold, W. and Russell, J., 1976, Equilibrium and Natural Frequencies of Cable Structures (a Nonlinear Finite Element Approach), Computers & Structures, Vol. 6, No. 4~5, pp. 267~271.
[https://doi.org/10.1016/0045-7949(76)90001-8]

-
Henghold, W. M., Russell, J. J. and Morgan, J. D., 1977, Free Vibrations of Cable in Three Dimensions, Journal of the Structural Division, Vol. 103, No. 5, pp. 1127~1136.
[https://doi.org/10.1061/JSDEAG.0004633]

-
Irvine, H. M., 1978, Free Vibrations of Inclined Cables, Journal of the Structural Division, Vol. 104, No. 2, pp. 343~347.
[https://doi.org/10.1061/JSDEAG.0004860]

-
Triantafyllou, M. and Grinfogel, L., 1986, Natural Frequencies and Modes of Inclined Cables, Journal of Structural Engineering, Vol. 112, No. 1, pp. 139~148.
[https://doi.org/10.1061/(ASCE)0733-9445(1986)112:1(139)]

- Chang, S. I., 1998, Bifurcation Analysis of Nonlinear Oscillations of Suspended Cables with 2-to-1 Internal Resonance, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 8, No. 6, pp. 1144~1149.
-
Desai, Y. and Punde, S., 2001, Simple Model for Dynamic Analysis of Cable Supported Structures, Engineering Structures, Vol. 23, No. 3, pp. 271~279.
[https://doi.org/10.1016/S0141-0296(00)00035-3]

-
Zhou, X., Yan, S. and Chu, F., 2011, In-plane Free Vibrations of an Inclined Taut Cable, Journal of Vibration and Acoustics, Vol. 133, No. 3, pp. 1~9.
[https://doi.org/10.1115/1.4003397]

-
Phanyasahachart, T., Athisakul, C. and Chucheepsakul, S., 2018, Natural Frequencies of a Very Large–sag Extensible Cable, Journal of Engineering Mechanics, Vol. 144, No. 2, pp. 1~7.
[https://doi.org/10.1061/(ASCE)EM.1943-7889.0001409]

- Klaycham, K., Nguantud, P., Athisakul, C. and Chucheepsakul, S., 2020, Free Vibration Analysis of Large Sag Catenary with Application to Catenary Jumper, Ocean Systems Engineering, Vol. 10, No. 1, pp. 67~86.
-
Impollonia, N., Ricciardi, G. and Saitta, F., 2011, Vibrations of Inclined Cables under Skew Wind, International Journal of Non-linear Mechanics, Vol. 46, No. 7, pp. 907~918.
[https://doi.org/10.1016/j.ijnonlinmec.2011.03.006]

-
Bearman, P. W., 1984, Vortex Shedding From Oscillating Bluff Bodies, Annual Review of Fluid Mechanics, Vol. 16, No. 1, pp. 195~222.
[https://doi.org/10.1146/annurev.fl.16.010184.001211]

-
Fujarra, A., Pesce, C., Flemming, F. and Williamson, C., 2001, Vortex-induced Vibration of a Flexible Cantilever, Journal of Fluids and Structures, Vol. 15, No. 3-4, pp. 651~658.
[https://doi.org/10.1006/jfls.2000.0368]

-
Gale, J. and Smith, C., 1983, Vibrations of Suspended Cables, Journal of Applied Mechanics, Vol. 50, No. 3, pp. 687~689.
[https://doi.org/10.1115/1.3167115]

-
Gupta, S. K., Malla, A. L. and Barry, O. R., 2021, Nonlinear Vibration Analysis of Vortex-induced Vibrations in Overhead Power Lines with Nonlinear Vibration Absorbers, Nonlinear Dynamics, Vol. 103, No. 1, pp. 27~47.
[https://doi.org/10.1007/s11071-020-06100-9]

-
Jafari, M., Hou, F. and Abdelkefi, A., 2020, Wind-induced Vibration of Structural Cables, Nonlinear Dynamics, Vol. 100, No. 1, pp. 351~421.
[https://doi.org/10.1007/s11071-020-05541-6]

-
Leblond, A. and Hardy, C., 2005, Unifying Calculation of Vortex-induced Vibrations of Overhead Conductors, Wind and Structures, Vol. 8, No. 2, pp. 79~88.
[https://doi.org/10.12989/was.2005.8.2.079]

-
Lepidi, M., Gattulli, V. and Vestroni, F., 2007, Static and Dynamic Response of Elastic Suspended Cables with Damage, International Journal of Solids and Structures, Vol. 44, No. 25~26, pp. 8194~8212.
[https://doi.org/10.1016/j.ijsolstr.2007.06.009]

-
Li, Z.-J., Li, P., He, Z. and Cao, P., 2013, Static and Free Vibration Analysis of Shallow Sagging Inclined Cables, Structural Engineering and Mechanics: An International Journal, Vol. 45, No. 2, pp. 145~157.
[https://doi.org/10.12989/sem.2013.45.2.145]

-
Rakočević, M. and Popović, S., 2018, Calculation Procedure for Determining Wind Action from Vortex-induced Vibration with Verification of Fatigue Strength of Steel Structures, Građevinar, Vol. 70, No. 9, pp. 793~809.
[https://doi.org/10.14256/JCE.2125.2017]

-
Zhao, M. and Cheng, L., 2014, Vortex-induced Vibration of a Circular Cylinder of Finite Length, Physics of Fluids, Vol. 26, No. 1, pp. 1~26.
[https://doi.org/10.1063/1.4862548]


Dae Woong Kim received B.S. in Mechanical Engineering from Dongguk University in 2022. He is currently a graduate student in the Dept. of Mechanical Engineering in Dongguk University.

Moon Kyu Kwak received B.S. and M.S. degrees in Naval Architecture from Seoul National University in 1981 and 1982. He then received his Ph.D. degree from the Dept. of Engineering Science and Mechanics of Virginia Tech in 1989. He is currently a Professor at the Department of Mechanical, Robotics and Energy Engineering of Dongguk University in Seoul, Korea. His research interests are dynamics and control of flexible multibody system and active vibration control of smart structure.