고각구동 프레임 구조물의 힌지 위치에 따른 최적설계 및 해석

1. 서 론

산업현장에서의 프레임 구조물은 전통적으로 고 중량의 물체를 지지하기 위해 고장력강으로 제작된다. 구체적으로 고 강도의 프레임 구조물은 건설현장에서의 크레인, 대형 수송기계의 구조장치, 방위산업 현장에서 무기체계 등의 구조장치에 널리 쓰인다. 일반적으로 이러한 대형 구조장치에 적용되는 고강도 프레임 구조는 필요 크기와 비용이 매우 크기 때문에 제작 사전의 설계 검토가 어떠한 기계장치 및 시스템 보다 더 중요하다. 이렇게 막대한 자원이 소모될 가능성이 있는 고 하중용 프레임 구조물의 설계 시에는 목표 시스템에 맞는 설계 변수를 확정 한 후 최적 성능을 발휘할 수 있게끔 하는 최적설계를 수행해야 한다. 이러한 목표 시스템에 맞는 최적 설계 법은 다양한 연구와 개발사례에 적용되어 왔다. 일반적으로 많이 사용되는 최적설계 프로그램은 Ansys, Nastran 등의 해석프로그램의 내부 최적화 모듈이다. Yim 등⁽¹⁾은 저진동 차체의 필라 설계를 위해 변형에너지 법을 적용하였고, Nastran을 이용하여 1차 고유진동수를 목표로 설계 민감도를 최적화하는 방법으로 최적 설계를 수행하였다. Park 등⁽²⁾은 함정 탑재장비의 진동저감을 위한 하부구조물의 최적 설계에 Nastran의 민감도 분석 및 최적화 기법을 적용하였다.

Chae 등⁽³⁾은 Nastran의 외부 호출형 최적화 기법을 적용한 Random-Tabu 탐색 법을 활용하여 구속조건에 따른 선박구조물의 종방향 및 횡방향의 전반적인 진동응답(변위, 속도, 가속도)을 평가하였다. Ha 등⁽⁴⁾은 MR 댐퍼의 댐핑력 성능을 최대로 발휘하기 위해서 필요한 설계 변수인 MR 유체의 항복응력을 목적함수로 설정하고 이론적인 MR 유체 자기장의 설계 변수 식을 기반으로 Ansys 내부 최적화 모듈을 활용하여 최적설계를 수행하였다. Nguyen 등⁽⁵⁾은 Ha 의 연구와 비슷한 방법으로 MR Brake의 최적 설계를 수행하였다.

여기에 추가적으로 설계 변수들의 변동 및 산포 등의 특징을 반영하기 위한 최적 설계 연구도 수행되었다. Song 등⁽⁶⁾은 차량 시스템을 구성하는 인자들의 산포들이 차량 승차감 변동에 미치는 영향을 분석하기 위해서 감도분석 및 산포해석을 이용한 강건 최적 설계를 수행하였다. Lim 등⁽⁷⁾은 설계변수의 이산적인 변동 불확실성을 예측하기 위해서 적절한 수학적 근사함수를 도입한 다음 Matlab 기반으로 입력된 이산 정보를 확률밀도함수로 정의하여 최적화된 목표 신뢰도를 예측하는 연구를 수행하였다.

그동안의 연구들을 확인해보면 최적 설계를 수행할 때 시스템의 수학적 모델과 설계변수를 확립한 뒤 프로그램의 내부 연산 모듈을 사용하여 반복적인 연산을 수행하고 난 다음, 해가 수렴 되면 채택 하는 방식으로 수행된다. 물론 이 방법은 이론적인 시스템 모델이 확립된 상황에서 다수의 설계 변수들이 존재할 때 매우 유용하다. 그러나 비교적 간단한 기하학적인 구조와 소수의 설계변수를 내제한 시스템에 대해서는 경제적으로 과도한 측면이 존재한다.

이 연구에서는 간단한 모델을 내제한 시스템에 대해서 해석프로그램의 내부 최적화 모듈을 사용하지 않고 직접적으로 최적 해를 도출하는 것을 시도하여 비교적으로 간단한 수학적 모델과 설계 변수를 내제한 시스템에 대해서 경제적인 최적 설계를 수행할 수 있는 방법을 찾고자 한다.

먼저 이 연구에서 최적 설계의 대상으로 채택한 시스템은 고각구동이 가능한 가변 힌지 위치 기반의 프레임 구조물이다. 이 구조물을 선택한 이유는 다음 2가지이다.

• (1) 산업현장에서 범용적으로 쓰인다.
• (2) 1-D와 3-D 모델간의 상사가 간단하다.

이 고각구동 프레임 구조물은 힌지 위치에 따라서 하중지지에 따른 끝단 처짐이 다르게 나타난다. 일반적으로 허용 공차가 요구되는 기계시스템에서 국부 처짐은 설계 시 고려돼야 하는 매우 중요한 변수이다. 이는 시스템 구동 시 구조간의 간섭에 영향을 주기 때문이다. 따라서 이 연구에서는 고각구동에 따른 프레임 구조의 최대 처짐을 최적 설계의 주 인자로 선정하였다. 그리고 프레임 구조의 무게는 제작비용을 선정하기 위한 중요한 변수이다. 그래서 이 시스템에서는 프레임의 무게와 힌지 위치에 따라 처짐이 다르게 발생되므로 프레임 무게와 힌지 위치를 독립 변수, 처짐을 종속 변수, 그리고 그 외 다른 변수들을 통제 변수로 설정한다. 다만, 사각 단면 구조를 가진 프레임의 무게는 길이에 정비례하기 때문에 이 연구에서는 무게 대신에 길이를 변수로 정한다. 그런 다음, 1-D의 기하학적 구조를 바탕으로 처짐 방정식 및 경계조건 식들을 도출하고 Matlab을 활용하여 기하학적인 최적 해(프레임 길이와 힌지 위치)를 찾고 3-D 기반의 유한요소해석(finite element analysis)을 통해 처짐 방정식과 해의 유효성을 검증하는 것을 목표로 한다.

2. 본 론

2.1 고각구동 프레임 구조 설계

(1) 설계 개요

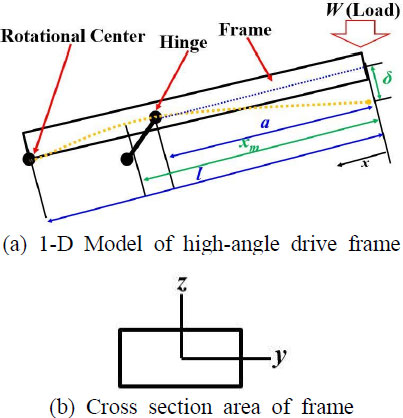
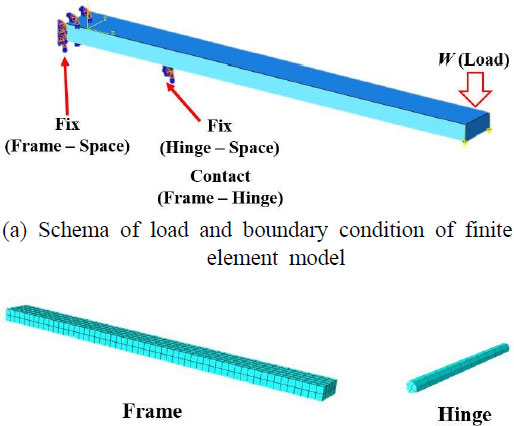
이 절에서는 이 연구의 설계 대상인 고각구동 프레임 구조를 설명한다. 고각구동 프레임 구조는 Fig. 1(a)에 보이는 바와 같이 1차원 구조의 외팔 보 형태에 힌지가 회전 중심에서 이격하여 프레임을 떠받드는 구조이다. 그리고 집중하중이 보의 끝단에 적용된다. 일반적으로 이러한 구조는 실제 현장에서는 분포하중 형태로 적용되지만 설계와 해석의 단순화를 위해 집중하중 형태로 가정하였다. 보의 단면 구조는 Fig. 1(b)에 보이는 바와 같이 사각 단면 구조로 정의하였다.

Fig. 1

Schema of high-angle drive frame

(2) 프레임 구조 처짐 수학적 모델

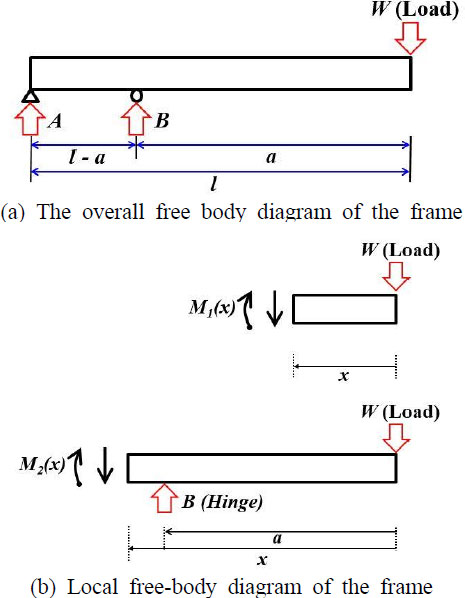
Fig. 1(a)은 도시된 프레임-힌지 구조를 기하학적으로 나타낸다. 여기서 W, l, a, δ, x_m은 각각 하중, 프레임의 길이, 하중과 힌지 사이의 거리, 처짐(deflection), 그리고 하중 적용 지점에서 최대 모멘트 사이의 거리이다. Fig. 2(a)은 프레임-힌지 구조의 자유물체도(free body diagram)이다. 여기서 A와 B는 각각 회전 중심에서의 연직방향 반력, 힌지에서의 연직방향 반력이다. 고각구동 프레임은 회전하기 직전에 최대 하중이 적용되므로 이 연구에서는 수평 상황에서 하중이 적용되는 것으로 가정하였다.

Fig. 2

The free body diagram of high-angle drive frame

이 연구에서 확인해야 하는 주 인자인 처짐은 Fig. 2에 도시된 자유물체도를 기반으로 도출 될 수 있다. 먼저 Fig. 2(a)에 따르면 다음과 같이 반력 A와 B를 나타낼 수 있다.

$\[ A=\frac{-W(l-a)}{a} \]$

(1)

$\[ B=\frac{Wl}{a} \]$

(2)

그리고 식 (1), (2), 그리고 Fig. 2(b)의 국부적인 프레임의 자유물체도를 이용하여 다음과 같이 적분법을 이용하여 프레임의 국부적인 모멘트-처짐 식을 도출할 수 있다⁽⁸⁾.

$\[ E{I\upsilon }^{\mathrm{\text{'}}\mathrm{\text{'}}}\left(x\right)=M\left(x\right)=\left(\frac{Wl}{a}-W\right)x-Wl \]$

(3)

$\[ E{I\upsilon }^{\mathrm{\text{'}}}\left(x\right)=\left(\frac{Wl}{a}-W\right)\frac{x^2}{2}-Wlx+C_1 \]$

(4)

$\[ \begin{array}{c}EI\upsilon \left(x\right)=\left(\frac{Wl}{a}-W\right)\frac{x^3}{6}-\frac{Wl}{2}{x}^2+C_{1}x+C_2\\ (0\le x\le l)\end{array} \]$

(5)

여기서 E, I, v(x), M(x), C₁, C₂는 각각 프레임의 탄성계수, 2차 단면모멘트, 국부 처짐, 국부 모멘트, 적분상수이다. 그리고 프레임의 처짐은 회전 중심과 힌지 고정점에서 0이고 끝단에서 최댓값을 가진다. 또한 힌지가 고정된 지점에서 프레임은 연속이므로 경계조건을 조합하면 다음과 같다.

$\[ \begin{array}{c}v\left(a\right)=0\\ v\left(l\right)=0\\ v\left(0\right)={\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}\end{array} \]$

(6)

경계조건 (6)을 식 (3)~(5)에 대입하면 프레임의 최대 처짐을 식 (7)과 같이 도출할 수 있다.

$\[ {\delta }_{\mathrm{m}\mathrm{a}\mathrm{x}}=\frac{W}{6EI}\left(a^2\left(2l+a\right)-\frac{4a{l}^3-l^4-2l{a}^3-a^4}{l-a}\right) \]$

(7)

(3) 경계 방정식 및 설계 변수 선정

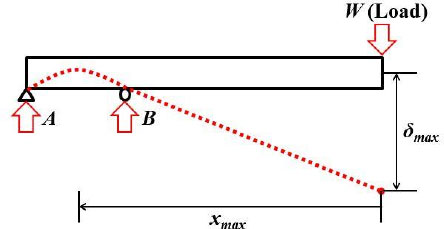
이 연구의 설계 대상인 프레임은 최대 모멘트 지점이 고각 회전 중심과 힌지 위치 사이에서 위치한다(Fig. 3). 이는 식 (4)와 (7), 그리고 2차 함수의 축의 방정식을 이용하면 다음과 같이 최대 모멘트의 지점을 도출할 수 있다.

(8)

$\[ x_{\mathrm{m}\mathrm{a}\mathrm{x}}=l-\sqrt{\frac{1}{3}{l}^2-\frac{2}{3}la+\frac{1}{3}{a}^2} \]$

(9)

Fig. 3

Location of maximum moment & deflection of the frame

그리고 이 연구에서는 힌지의 위치를 프레임의 길이의 절반 보다는 크고 이 길이 보다는 작다고 가정하였다. 이를 식으로 나타내면 다음과 같다.

(10)

프레임의 길이와 힌지 위치를 제외한 나머지 변수들은 Table 1에 정리된 바와 같다. 여기서 δ_o는 프레임의 최대 목표 처짐이다.

Table 1

Design variables of the frame

2.2 기하학적 해 도출

이 절에서는 수식 계산 도구(Matlab)와 2.1 절에서 도출된 처짐 및 경계 방정식, 그리고 설계 변수들을 이용하여 최적 해를 찾는 내용을 기술한다. 식 (7) ~ (10) 및 Table 1의 내용을 기반으로 처짐 및 경계방정식을 도출하면 Table 2의 내용과 같이 도출할 수 있다. 그리고 Matlab의 ezplot 기능을 이용하여 다음과 도출된 식들을 다음과 같이 기하학적인 해(geometric solution)를 도출할 수 있다.

$\[ \begin{array}{l}\mathrm{O}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}:F\left(x\right)\le 20;\\ \mathrm{S}\mathrm{u}\mathrm{b}\mathrm{j}\mathrm{e}\mathrm{c}\mathrm{t}\mathrm{ }\mathrm{t}\mathrm{o}:\begin{array}{l}{G}_3\left(x\right)\le 0;\\ G_4\left(x\right)\le 0;\end{array}\\ \mathrm{S}\mathrm{i}\mathrm{d}\mathrm{e}\mathrm{ }\mathrm{C}\mathrm{o}\mathrm{n}\mathrm{s}\mathrm{t}\mathrm{r}\mathrm{a}\mathrm{i}\mathrm{n}\mathrm{t}\mathrm{s}:x_2\ge x_1;x_2\le 2x_1;\end{array} \]$

(11)

Table 2

The boundary equation of the system

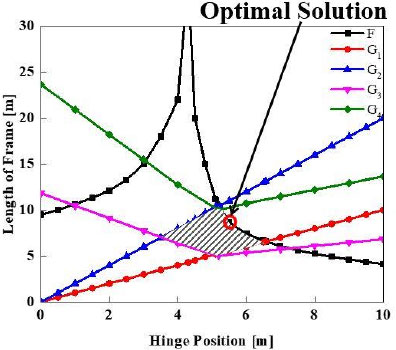
계산 결과 목표 처짐 20 mm로 가정하였을 때, 최적 해는 Fig. 4에 빗금 표시된 영역에 존재한다. 이 영역에서는 선택가능한 해가 매우 많기 때문에 실제 현장에서 설계 변수를 선택하기 위해서는 경계방정식의 영역을 줄여나가면서 해를 선택하면 된다. 이 연구에서는 적절한 해를 선택하였다. 선택한 해는 다음과 같다.

$\[ \begin{array}{c}a=x_1^{*}=\mathrm{5,550}\\ l=x_2^{*}=\mathrm{8,500}\end{array} \]$

(12)

Fig. 4

Result of selecting optimal solution for deflection equation via geometric solution

2.3 유한 요소 해석

(1) 개요

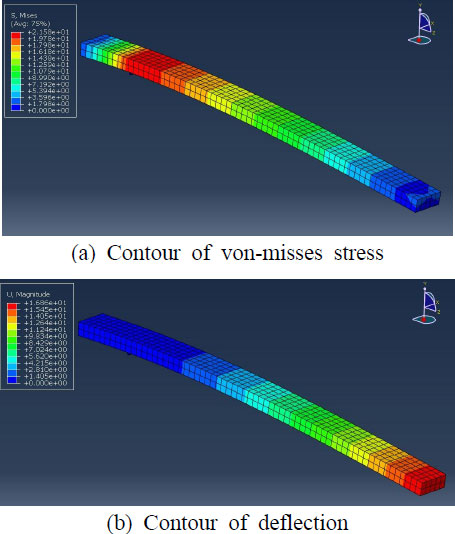
이 절에서는 유한요소해석을 이용하여 2.1절에서 도출된 프레임의 처짐 식 (7)과 2.2절에서 도출된 최적 해의 유효성을 검증한다. 해석에 사용된 프로그램은 Abaqus이고 정적해석 모듈을 이용하였다. 그리고 Fig. 5(a)에 도시된 바와 같이 프레임을 힌지에 걸쳐두고 접촉(contact)조건을 적용하였고 끝단과 공간(space), 힌지와 공간 사이에 fix 조건을 적용하였다. 유한요소의 형상은 Fig. 5(b)에 표시된 바와 같다. 그리고 유한요소의 종류와 물성 값과 크기, 개수 등의 정보는 Table 3에 정리되어있다. 해석을 수행하면 Fig. 6과 같이 결과가 도출된다. Fig. 6(a)는 von-mises stress, Fig. 6(b)는 처짐을 각각 표현한다. 프레임의 재질은 고장력강이고 최대 응력 해석 결과 값이 항복 응력의 약 3 % 수준이므로 이 연구에서는 강도에 대한 결과를 고려하지 않는다.

Fig. 5

Information of finite element analysis for high-angle drive frame

Table 3

Information of finite element

Fig. 6

Picture of finite element analysis

(2) 처짐 모델 검증 해석

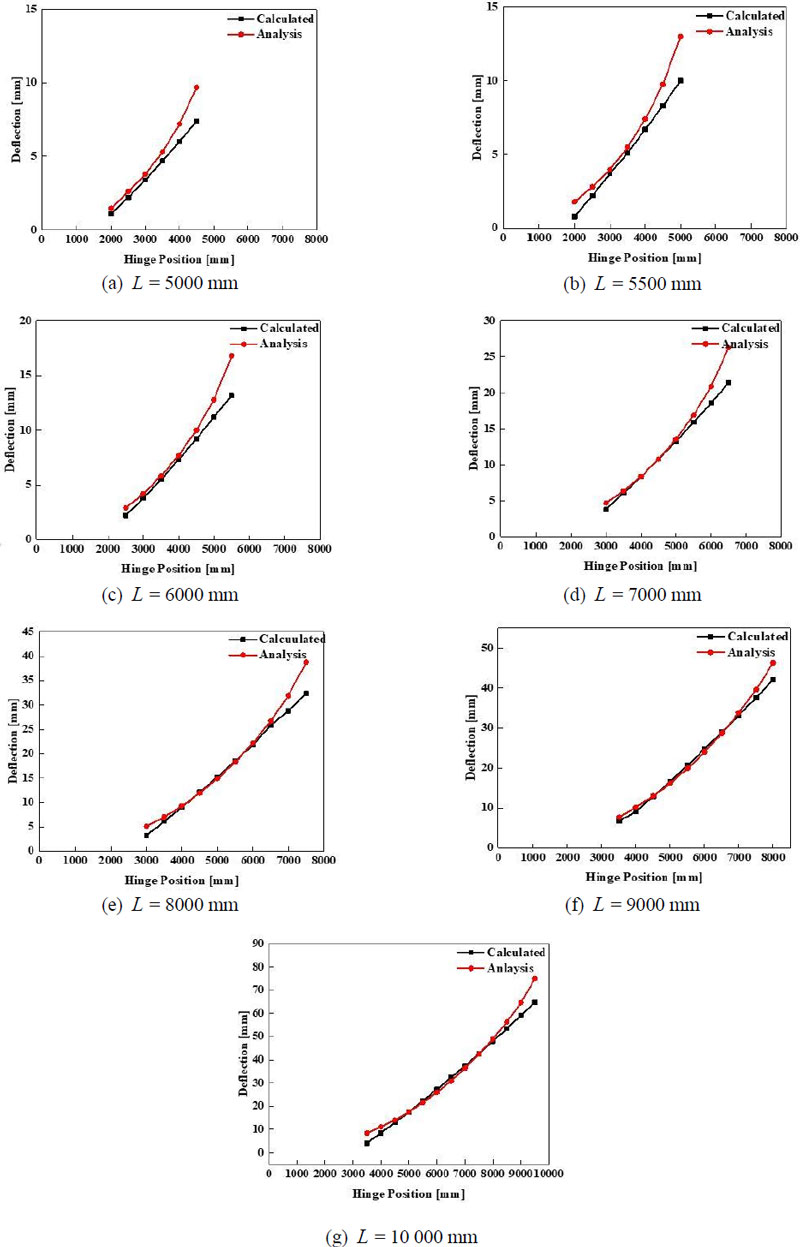
이 해석에서는 1-D 기반으로 도출되었던 프레임의 처짐 식 (7)을 검증하기 위해 동일한 크기에 너비만 추가된 3-D 기반 해석을 수행한다. 프레임 길이와 힌지의 2변수에 의한 결과를 도출해야 하므로 상당히 많은 수의 해석을 수행하였다. 해석 case는 프레임 길이 기준으로 7개, 힌지 위치 기준으로 8개 총 56개다. 처짐 모델 검증 해석 결과는 Fig. 7에 도시된 바와 같다. 그림에 표시된 선도는 힌지 위치에 따른 처짐 값이다. 검은색과 빨간색은 각각 식 (7)에 의해 계산된 값, 해석 결과 도출된 값이다.

Fig. 7

Analysis results of deflection equation model verification

해석 결과의 선도를 분석해보면 직선 형태의 계산식 선도와는 다르게 곡선형을 띈다. 그리고 프레임 길이가 작을 때는 계산 값과 해석 값의 오차가 비교적 크게 존재하다가 길이가 증가할수록 감소하는 경향을 보인다. 이를 상세하게 살펴보면 프레임 길이가 5000 mm ~ 6000 mm일 때 힌지 위치가 약 40 % ~ 66 % 구간에서 오차가 감소하는 경향이 있고 그 최댓값은 24.4 %, 최솟값은 6.6 %이다. 반면에 프레임 길이가 7000 mm 이상인 구간에서는 힌지 위치가 약 50 % ~ 75 % 구간에서 오차의 최댓값이 3.4 %이고 최솟값은 0.1 % 수준으로 나타난다. 이는 프레임 길이 7000 mm 이상의 구간에서 계산식이 해석 값 기준으로만 보았을 때 비교적 정확하다는 것을 알 수 있다.

(3) 최적 해 검증 해석

이 해석에서는 2.2절에서 도출한 기하학적 최적 해의 유효성을 검증한다. 검증 방법은 다음과 같다.

• 1) 처짐 계산식에 최적 프레임 길이일 때 힌지 위치에 따른 처짐 값 확인
• 2) 처짐 계산식에 최적 힌지 위치일 때 프레임 길이에 따른 처짐 값 확인
• 3) 해석 결과와 비교 후 일정 오차 범위(5 % 이내)에 존재 여부 확인

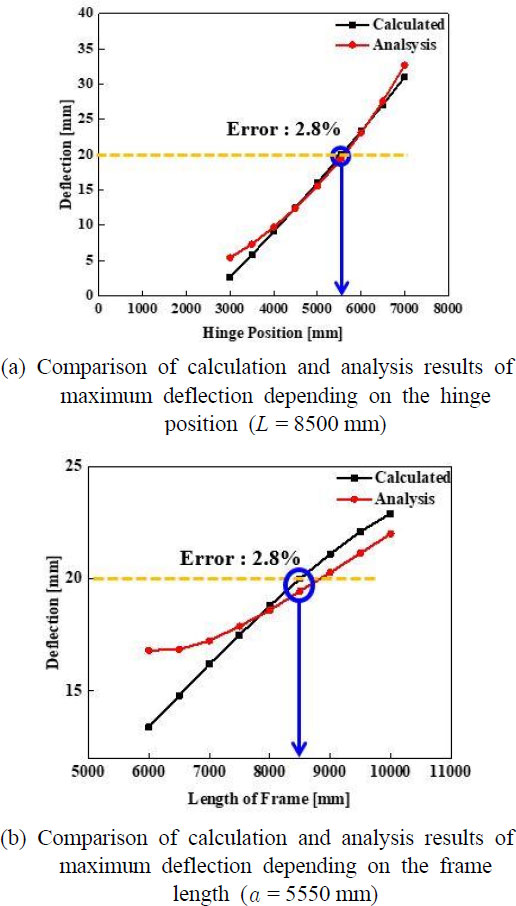
해석 결과는 Fig. 8에 도시된 바와 같다. Fig. 8(a)의 결과를 확인해 보면 프레임 길이가 8500 mm 일 때 힌지 위치 5550 mm에서 도출되는 처짐 값은 계산 값과 해석 값 각각 20 mm, 19.45 mm이다. 오차는 약 2.8 %이다. 그리고 Fig. 8(b)의 반대상황에서의 결과도 동일하다. 특히 프레임의 길이에 따른 처짐 값 계산 및 해석 결과를 주목해 보면 처짐 20 mm이고 힌지 위치 5550 mm일 때 프레임 길이 약 7800 mm 부근 이하의 구간과 9000 mm 이상 구간에서는 오차가 증가하는 것을 확인할 수 있다. 그러므로 프레임 길이가 8000 mm 이상 9000 mm 이하 구간에서 목표 처짐 오차 범위 안쪽의 해가 존재한다는 것을 확인할 수 있다. 따라서 도출된 최적 해는 적절하다는 것을 확인할 수 있다.

Fig. 8

Analysis results for optimal solution verification

3. 결 론

이 연구에서는 고 하중을 견디는 고각구동 프레임의 길이와 힌지 위치의 처짐 방정식에 따른 기하학적인 최적 해의 탐색을 통한 최적 설계를 다음의 절차로 수행하였다.

(1) 프레임 길이와 힌지 위치에 따른 최대 처짐 계산식 및 경계조건 방정식 도출

(2) 최대 처짐 계산식 및 경계조건 방정식을 Matlab ezplot 기능을 이용하여 목표 처짐 일 때, 기하학 적인 해(최적 프레임 길이, 최적 힌지 위치) 도출

(3) 유한요소 정적해석을 이용하여 도출된 처짐 계산식 및 최적 해 유효성 검증 완료

이 연구결과를 통하여 설계 상황이 비교적 단순한 고각구동 프레임 시스템(혹은 일반 프레임지지 시스템)에서는 최적 설계 기법중 기하학적인 해 도출 방법(geometric solution)을 통하여 1-D 기반의 수식 계산을 통해서도 3-D 해석 결과와 유사한 설계 결과를 도출할 수 있다는 것을 알 수 있다. 따라서 이 연구에서 제안한 최적 설계법을 이용하면 비용과 시간적인 측면에서 매우 경제적인 설계를 할 수 있을 것으로 기대된다.

References

• Yim, H. J. and Lee, S. B., 1995, Technology for Initial Design and Analysis of Vehicle Pillar Structure for Vibration, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 5, No. 3, pp. 395~402.
• Park, S. H., Han, H. S., Lee, K. H. and Jeon, S. H., 2016, Optimization of Vibration for Shipboard Equipment, Proceedings of the KSNVE Annual Spring Conference, pp. 312~313.
• Chae, S. I., Song, J. D., Kim, Y. H., Yang, B. S., Kong, Y. M. and Choi, S. H., 2003, Vibration Optimization Design of Ship Structure Using NASTRAN-based R-Tabu Search Method, Proceedings of the KSNVE Annual Autumn Conference, pp. 672~676.
• Ha, S. H., Seong, M. S., Nguyen, Q. H. and Choi, S. B., 2009, Optimal Design of MR Damper: Analytical Method and Finite Element Method, Proceedings of the KSNVE Annual Spring Conference, pp. 581~586.
• Nguyen, Q. H., Han, C. H., Lee, T. H., An, J. H. and Choi, S. B., 2018, Optimal Design of MR Brake with Magnetic Coils Located on the Housings, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 29, No. 1, pp. 13~20. [https://doi.org/10.5050/KSNVE.2019.29.1.013]
• Song, P. G., Spiriyagin, M. and Yoo, H. H., 2008, Robust Design Optimization of the Vehicle Ride Comfort Considering Variation of the Design Parameters, Transactions of the Korean Society for Noise and Vibration Engineering. Vol. 18, No. 12, pp. 1217~1223. [https://doi.org/10.5050/KSNVN.2008.18.12.1217]
• Lim, W. C., Jang, J. Y,, Kim, J. H., Na, J. H., Lee, C. K., Kim, Y. S. and Lee, T. H., 2014, Reliability-based Design Optimization Considering Variable Uncertainty, Transactions of Mechanical Engineers A. Vol. 38, No. 6, pp. 649~653. [https://doi.org/10.3795/KSME-A.2014.38.6.649]
• Roy, R. C., 2009, Mechanics of Materials, John Wiley & Sons, Inc., New York.