실시간 상태-공간 식별 기반 제어기를 이용한 유한 국부공진 메타물질 평판의 적응형 진동 저감

1. 서 론

환경 규제로 이산화탄소 배출량 감소가 산업 전반에 걸쳐 요구됨에 따라, 전 세계적으로 기존의 내연기관 차량에서 전기 차량으로 빠른 교체가 진행되고 있다. 기존의 내연기관 차량과 달리, 전기 차량의 내부소음에서는 내연기관의 소음으로 인한 마스킹 효과가 존재하지 않는다. 결과적으로, 전기 차량의 내부음질 개선을 위해서는 내연기관 차량 대비 타이어 및 노면 소음과 같은 부차적인 소음의 효과적인 저감이 요구된다⁽¹⁾. 일반적으로 차량의 내부소음 저감을 위한 소음, 진동 및 불쾌감(noise, vibration, and harshness, NVH) 해결책은 구조-기인 소음의 전달 경로에 감쇠재료를 부착하는 것이다⁽²⁾. 하지만, 감쇠재료는 저주파수 대역의 진동 저감 및 경량화 설계에 불리하다⁽³⁾.

차량의 NVH에서 기존의 감쇠재료의 단점을 극복하기 위해, 음향메타물질의 사용이 고려된다. 음향메타물질은 자연상의 물질로부터 정지대역 특성을 갖도록 설계된 물질이다⁽⁴⁾. 정지대역은 호스트 구조에 음향메타물질을 부착하여 파동의 전파를 차단함으로써 형성된다. 일반적으로, 음향메타물질에서 정지대역을 형성하는 방법은 음향양자결정(phononic crystals, PC)과 국부공진 메타물질(locally resonant metamaterials, LRM)로 분류된다⁽⁵⁾. LRM은 PC와 달리 단위 구조들이 파장 이하 간격으로 배치될 필요가 없으므로, 진동 저감을 위한 NVH 해결책으로 적합하다^(6~8).

LRM을 차량의 NVH에 적용하기 위한 최신 연구들은 주로 LRM의 생산성 및 설치 편의성 향상을 중심으로 진행되었다. 일반적으로, 생산성 및 설치 편의성을 만족하는 LRM은 많은 수의 단위 구조들을 한 번에 생산 및 부착할 수 있도록 만들어져 있으며 곡면에 쉽게 부착할 수 있도록 유연한 구조를 갖는다. Kim 등⁽⁹⁾은 LRM의 단위 구조들이 서로 연결됐을 때 정지대역에 미치는 영향을 조사하였다. Yu 등⁽¹⁰⁾은 표면의 곡률이 LRM의 정지대역에 미치는 영향을 조사하였다. Kim 등⁽⁹⁾과 Yu 등⁽¹⁰⁾의 연구는 각각 LRM의 연결성 및 표면의 곡률이 LRM의 정지대역 형성에 유의한 영향을 미치지 않는 것을 보여줬다. 하지만, Sangiuliano 등⁽⁴⁾의 연구에 따르면 호스트 구조의 경계 조건은 LRM의 정지대역 형성에 부정적인 영향을 미친다. 일반적으로, LRM의 정지대역은 무한한 표면에 단위 구조들이 무한히 배열되는 경우에 대해 설계된다. 이 경우, LRM의 정지대역에 해당하는 주파수 대역에서는 진동모드가 존재하지 않는다⁽⁹⁾. 반면, 실제 호스트 구조는 유한하며 배치되는 단위 구조의 수 또한 제한된다. 결과적으로, 실제 호스트 구조에 적용된 LRM이 형성하는 정지대역에서는 진동모드가 발생한다. Sangiuliano 등⁽⁴⁾의 연구는 호스트 구조의 경계 조건 뿐 아니라 가진력과 LRM의 위치에 따라 정지대역 내 진동모드가 발생하는 주파수가 달라지는 것을 보여줬다. 결과적으로, 임의의 호스트 구조에 대해 완벽한 정지대역을 갖는 LRM의 설계는 어렵다.

LRM의 정지대역 내의 임의의 주파수에서 발생하는 진동모드를 효과적으로 저감하려면, 적응 필터에 기반한 능동진동제어(active vibration control, AVC)가 적합하다. AVC에서 적응 필터는 실시간 시스템 식별을 통해 얻은 정보를 바탕으로 변동하는 시스템에 대해 최적의 진동 저감 성능을 얻고자 사용된다. Rew 등⁽¹¹⁾의 연구에서, 구조물의 진동 저감을 위해 고유진동수 식별에 기반한 양변위 되먹임(positive position feedback, PPF) 제어기가 사용됐다. Zhang 등^(12,13)의 연구에서, 구조물의 진동 저감을 위해 이력 식별에 기반한 최소 분산 자기-동조 직접 레귤레이터(minimum variance self-tuning direct regulator, MVSTDR)를 갖는 제어기가 사용됐다. Rew 등⁽¹¹⁾과 Zhang 등^(12,13)의 연구에서 사용된 AVC 방법은 모두 시스템 전달함수에 기반한 고전 제어에 속한다. 만약 구조물의 고유진동수 뿐만 아니라 모드형상에 대한 정보를 알고 있으면, 제어되지 않는 배경 모드의 영향을 배제하여 최적의 진동모드 저감 달성이 가능하다⁽¹⁴⁾. 이는 상태-되먹임에 기반한 현대 제어가 고전 제어보다 진동모드 저감에 유리함을 의미한다. 그렇지만, 현대 제어가 사용된 기존의 AVC 연구들은 해석적 혹은 실험적 모델에 기반하여 상태-공간 식별이 수행되었다^(15,16). 해당 상태-공간 식별 방법들은 오프라인 상에서만 수행될 수 있다. 결과적으로, 현대 제어가 사용된 기존의 AVC 연구들은 변동하는 시스템에 적용하는 데 한계가 있다.

이 연구에서는 LRM의 정지대역 내의 임의의 주파수에서 발생하는 진동모드를 저감하기 위한 실시간 상태-공간 식별 기반 AVC 방법이 제안된다. 이전의 AVC 연구에선 오프라인 상에서 추정된 상태-공간 모델이 상태 관측기 및 최적 제어기를 위해 사용되었다. 제안되는 방법은 실시간 상태-공간 식별을 통해 상태-공간 모델을 실시간으로 추정함으로써 호스트 구조의 경계 조건, 가진력과 LRM의 위치에 따라 달라지는 시스템에 효과적으로 적응한다. 게다가, 제안되는 방법은 상태-되먹임에 기반한 현대 제어를 통해 최적의 진동모드 저감이 가능하다.

이 논문은 다음과 같이 구성된다. Section 2는 실시간 상태-공간 식별의 개념을 설명한다. Section 3은 유한 LRM 평판을 위한 AVC 시스템의 설계를 설명한다. Section 4는 유한요소 모델과 Simulink를 사용한 시뮬레이션을 통해 유한 LRM 평판의 정지대역 내 진동모드 저감을 검증한다. 마지막으로, Section 5는 이 논문의 결론을 제시한다.

2. 실시간 상태-공간 식별의 개념

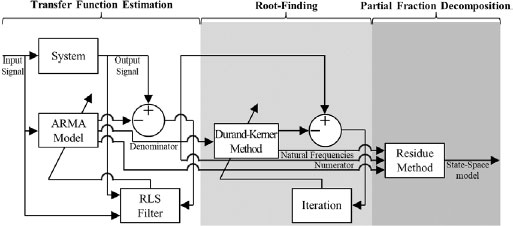
실시간 상태-공간 식별을 위한 식별기는 3단계로 구성된다. 첫 번째 단계는 전달함수 추정이다. 이 단계에서, 시스템의 전달함수는 재귀적 최소자승(recursive least squares, RLS) 필터를 통해 자기회귀 이동평균(autoregressive moving average, ARMA) 모델을 적응시킴으로써 추정된다. 두 번째 단계는 근찾기이다. 이 단계에서, 시스템의 고유진동수는 Durand-Kerner 방법을 통해 전달함수의 분모 다항식의 근을 반복적으로 구함으로써 추정된다. 세 번째 단계는 부분분수분해이다. 이 단계에서, 시스템의 상태-공간 모델은 유수 방법을 통해 전달함수의 부분분수분해를 수행함으로써 추정된다. 유수 방법을 사용하기 위해, 각각 첫 번째와 두 번째 단계로부터 얻어진 전달함수의 분자 다항식과 고유진동수가 요구된다. Fig. 1은 실시간 상태-공간 식별을 위한 식별기의 개념안을 보여준다.

Fig. 1

Outline of the identifier for real-time state-space identification

2.1 전달 함수의 추정

목표 주파수 대역에서 지배적인 진동모드의 수가 p라고 가정될 때, 이산-시간 선형 시스템의 전달함수는 다음과 같이 유리함수의 형태로 표현될 수 있다⁽¹¹⁾.

$\[ H\left(z^{-1}\right)\begin{array}{l}=\frac{N\left(z^{-1}\right)}{D\left(z^{-1}\right)}\\ =\frac{b_1{z}^{-1}+b_2{z}^{-2}+\cdots +b_{2p}{z}^{-2p}}{1+a_1{z}^{-1}+a_2{z}^{-2}+\cdots +a_{2p}{z}^{-2p}},\end{array} \]$

(1)

여기서 D(z^-1)와 N(z^-1)는 각각 AR과 MA 부분을 나타내는 분모 그리고 분자 다항식이다. Jeon 등⁽¹⁷⁾에 의하면, 식 (1)의 AR과 MA 부분은 각각 시스템의 고유진동수와 모드형상에 관한 항이다. Rew 등⁽¹¹⁾의 연구에서는, PPF 제어기를 사용하기 위해 시스템의 고유진동수에 대한 정보만 필요했다. 반면, 상태-되먹임 제어기를 사용하기 위해서는 시스템의 고유진동수와 모드형상에 대한 정보가 모두 필요하다. 따라서, 이 연구에서는 시스템의 전달함수 추정을 위해 AR과 MA 부분이 모두 적응된다.

AR과 MA 부분의 적응을 위한 적응 필터로, RLS 필터가 사용된다. RLS 필터의 사용을 위해, 우선적으로 다음과 같이 식 (1)을 시스템의 입력 u(k)와 출력 y(k)에 대한 ARMA 모델로 나타낼 필요가 있다⁽¹²⁾.

$\[ D\left(z^{-1}\right)y\left(k\right)=N\left(z^{-1}\right)u\left(k\right)+\xi \left(k\right) \]$

(2)

여기서 ξ(k)는 랜덤 외란이며 k는 샘플 포인트이다. 다음으로, 식 (2)는 다음과 같이 신호 벡터 ϕ(k)와 매개변수 벡터 θ에 대한 최소자승 형태로 표현된다:

$\[ y\left(k\right)={\mathit{\varphi }}^T\left(k\right)\mathit{\theta }+\xi \left(k\right) \]$

(3)

여기서

$\[ \left\{\begin{array}{c}\mathit{\varphi }\left(k\right)={\left[\begin{array}{l}-y(k-1),\cdots ,-y(k-2p),\\ u\left(k\right),\cdots ,u(k-2p)\end{array}\right]}^T\\ \mathit{\theta }={\left[a_1,\cdots ,a_{2p},b_1,\cdots ,b_{2p}\right]}^T\end{array}\right. \]$

(4)

식 (3)으로부터, 추정 출력 $$ \widehat{y}\left(k\right)$$는 다음과 같이 신호 벡터와 추정 매개변수 벡터 $$ \widehat{\mathit{\theta }}$$로부터 계산됨을 알 수 있다.

$\[ \widehat{y}\left(k\right)={\mathit{\varphi }}^T\left(k\right)\widehat{\mathit{\theta }} \]$

(5)

그러면, 실제 출력과 추정 출력 사이의 오차 ϵ(k)는 다음과 같이 주어진다:

$\[ ϵ\left(k\right)=y\left(k\right)-\widehat{y}\left(k\right)=y\left(k\right)-{\mathit{\varphi }}^T\left(k\right)\widehat{\mathit{\theta }} \]$

(6)

적응 필터 알고리즘들은 공통적으로 실제 출력과 추정 출력 사이의 오차를 최소화하도록 추정 매개변수 벡터를 업데이트한다. RLS 필터 알고리즘을 위한 공식은 다음과 같다⁽¹⁸⁾.

$\[ \left\{\begin{array}{c}\widehat{\mathit{\theta }}\left(k\right)=\widehat{\mathit{\theta }}\left(k-1\right)+K\left(k\right)\left[y\left(k\right)-{\mathit{\varphi }}^T\left(k\right)\widehat{\mathit{\theta }}\left(k-1\right)\right]\\ K\left(k\right)=\frac{{\lambda }^{-1}\mathbf{P}\left(k-1\right)\mathit{\varphi }\left(k\right)}{1+{\lambda }^{-1}{\mathit{\varphi }}^T\left(k\right)\mathbf{P}\left(k-1\right)\mathit{\varphi }\left(k\right)}\\ P\left(k\right)={\lambda }^{-1}\left[1-\mathbf{K}\left(k\right){\mathit{\varphi }}^T\left(k\right)\right]P\left(k-1\right)\end{array}\right. \]$

(7)

여기서 K(k), P(k), 그리고 λ는 각각 이득 행렬, 공분산 행렬, 그리고 망각계수이다. 식 (7)에서 보여졌듯이, RLS 필터는 추정된 변수의 보다 나은 수렴을 위해 초기값들 $$ \widehat{\mathit{\theta }}\left(0\right)$$, P(0)와 망각계수 λ의 값의 적절한 설정이 필요하다. Rew 등⁽¹¹⁾의 연구를 참고하여, 이 연구에서 사용된 RLS 필터의 매개변수는 Table 1과 같다. 또한, 계산비용과 진동저감 성능을 모두 고려하여 목표 주파수 대역에서 지배적인 모드의 수 p는 5로 선정되었다.

Table 1

Parameters of the RLS filter

3. 유한 LRM 평판을 위한 AVC 시스템의 설계

3.1 유한 LRM 평판

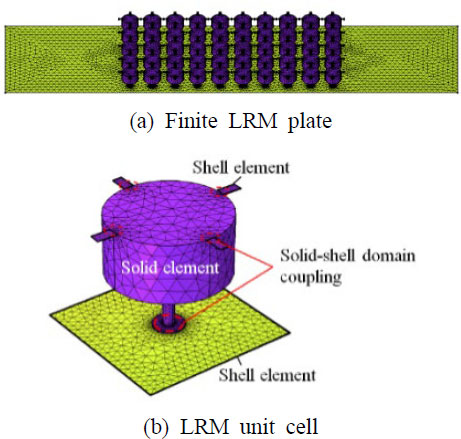
자유-지지되는 유한 평판에 LRM, 가속도계 및 액추에이터가 부착된 벤치마킹 모델이 Fig. 2에 나와 있다. 평판에 가해지는 진동은 평판의 맨 끝에 부착된 외란 액추에이터를 통해 생성되며, 평판의 중앙에 부착된 LRM을 통해 목표 주파수 대역에서 일차적으로 저감된다. LRM을 통해 저감되지 않는 진동은 평판의 양쪽에 부착된 가속도계와 제어 액추에이터 쌍을 통해 추가적으로 저감된다. 이때, 가속도계와 제어 액추에이터 쌍은 LRM에 의해 저감되지 않은 목표 주파수 대역 내 공진을 탐지하기 위해 LRM을 사이에 두고 설치되어야 한다. 벤치마킹 모델의 자세한 매개변수는 Table 2에 나와 있다. Table 2의 매개변수는 유한 LRM 평판과 LRM 단위 구조의 기하학적 매개변수와 물성으로 구성된다. Fig. 3는 Fig. 2의 벤치마킹 모델을 COMSOL에 기반한 유한요소 모델로 구현한 것을 보여준다. 이 연구에서 사용된 유한요소 모델은 Kim 등⁽⁹⁾이 수행한 유한 LRM 평판의 수치적 연구에서 사용된 유한요소 모델과 동일하다. 유한 평판에 적용된 LRM의 밴드구조(wave dispersion curve) 및 정지대역 설계 과정은 Kim 등⁽⁹⁾의 연구에 자세히 수록되었다. Kim 등⁽⁹⁾의 연구를 참고하여, LRM의 정지대역 내에서 진동모드가 발생하는 주파수 대역은 1000 Hz ~ 1600 Hz이다. 이 연구에서는 해당 주파수 대역을 AVC 시스템의 목표 주파수 대역으로 선정하였으며, 이에 따라 샘플링 주파수는 3200 Hz로 선정되었다.

Fig. 2

Benchmarking model of a finite LRM plate with AVC system

Table 2

Parameters of the benchmarking model in Fig. 2

Fig. 3

Finite element model of the benchmarking model in Fig. 2 using COMSOL

3.2 제어기 설계

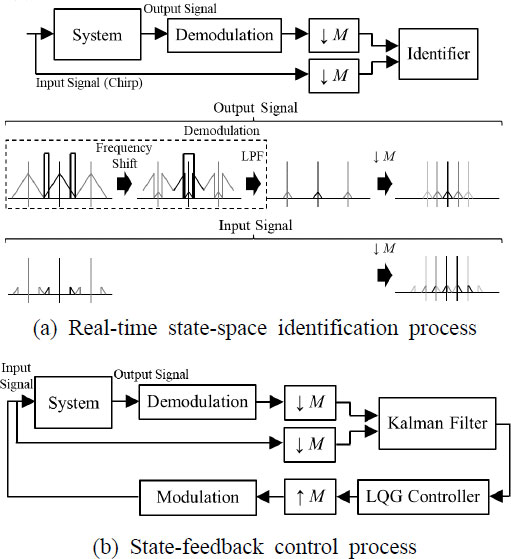
LRM의 정지대역에서 발생하는 진동모드를 저감하기 위한 AVC 시스템은 Fig. 4와 같이 실시간 상태-공간 식별 과정과 상태-되먹임 제어 과정으로 구성된다. Section 2에서 언급되었듯이, 실시간 상태-공간 식별기가 학습할 수 있는 최대 진동모드 수는 계산비용의 문제로 제한된다. 따라서, 목표 주파수 대역의 진동모드만을 학습하기 위해 시스템의 입력 및 출력 신호의 대역폭이 제한될 필요가 있다. Fig. 4(a)를 보면, 출력 신호의 대역폭은 주파수 이동과 저역통과 필터로 구성된 복조(demodulation) 과정과 다운샘플링을 통해 제한될 수 있다. 학습하고자 하는 목표 주파수 대역의 하한 및 상한 주파수가 각각 f_low와 f_high로 정의될 때, 복조를 위한 공식은 다음과 같다⁽²⁴⁾.

$\[ \left\{\begin{array}{c}\tilde{y}\left(k\right)=2y_{LPF}\left(k\right)*\left[y\left(k\right)e^{-i2\pi f_{\mathrm{l}\mathrm{o}\mathrm{w} }k{T}_s}\right]\\ Y_{LPF}\left(e^{i\omega }\right)=\left\{\begin{array}{cc}1& 0\le \left|\omega \right|\le 2\pi f_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h} }{T}_s\\ 0& 2\pi f_{\mathrm{h}\mathrm{i}\mathrm{g}\mathrm{h} }{T}_s⟨\left|\omega \right|\le \pi \end{array}\right.\end{array}\right. \]$

(22)

Fig. 4

Outline of the AVC system for a finite LRM plate

최종적으로, 복조 후 샘플링 주파수를 다운샘플링함으로써 출력 신호 대역의 하한 및 상한 주파수는 각각 0 Hz와 (f_high - f_low) Hz가 된다. 입력 신호의 경우, Fig. 4(a)에서 보여졌듯이 목표 주파수 대역만을 가진하는 chirp 신호를 사용함으로써 복조 과정 없이 다운샘플링만으로 대역폭 제한이 가능하다. 다운샘플링 계수가 M일 때, 주파수 왜곡 없이 대역폭 제한이 가능한 조건은 다음과 같다.

(23)

복조 과정을 거친 신호는 실수 신호보다 많은 계산비용이 요구되므로, chirp 신호의 사용이 가능한 입력 신호는 복조 과정을 거치지 않는 것이 계산비용 면에서 유리하다. 또한, 상태-되먹임 제어 과정을 위해서는 시스템의 상태를 관측하고 제어하기 위한 상태-관측기와 최적 제어기가 필요하다. Han 등⁽¹⁵⁾의 연구를 참고하여, 이 연구에서는 상태-관측기와 최적 제어기로 각각 칼만필터(Kalman filter)와 선형-이차-가우시안(linear-quadratic-gaussian, LQG) 레귤레이터가 사용되었다. 칼만필터와 LQG 레귤레이터는 모두 RLS 기반 적응 필터로서, 이득 행렬 K(k)를 실시간으로 계산하기 위해 식 (7)의 공식이 동일하게 적용될 수 있다. 이 연구에서 사용된 칼만필터와 LQG 레귤레이터의 매개변수는 각각 Table 3와 Table 4에 나와 있다. 또한, 상태-되먹임 제어 과정에서는 Fig. 4(b)와 같이 제어 입력 신호의 복조 과정과 제어 출력 신호의 변조(modulation) 과정이 동시에 수행된다. 변조를 위한 공식은 다음과 같다⁽²⁴⁾.

$\[ u\left(k\right)=Re\left[\tilde{u}\left(k\right)e^{i2\pi f_{\mathrm{l}\mathrm{o}\mathrm{w} }k{T}_s}\right] \]$

(24)

Table 3

Parameters of the Kalman filter for a single vibration mode

Table 4

Parameters of the LQG regulator for a single vibration mode

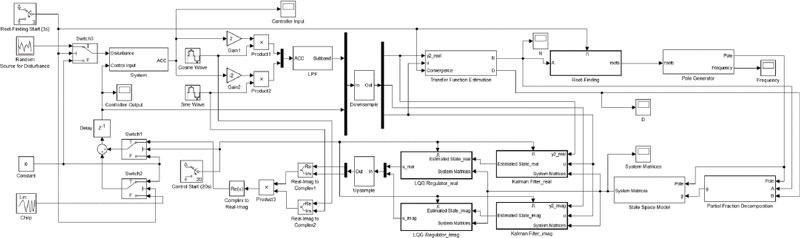
최종적으로, Fig. 5는 유한 LRM 평판을 위한 AVC 시스템을 Simulink로 구현한 것을 보여준다.

Fig. 5

Simulink block diagram of the AVC system for a finite LRM plate

4. 시뮬레이션 검증

1000 Hz ~ 1600 Hz의 목표 주파수 대역에서 유한 LRM 평판의 진동 저감을 위한 AVC 시뮬레이션이 Simulink에서 수행되었다. 시뮬레이션 시간은 총 40 s이며, 0 s ~ 3 s 동안의 전달함수 추정과 3 s ~ 3.01 s동안의 고유진동수 추정, 그리고 20 s ~ 40 s 동안의 제어 후 진동 저감 과정으로 구성된다. 시뮬레이션 결과는 실시간 상태-공간 식별과 제어 결과로 구분하여 검증이 진행되었다.

4.1 실시간 상태-공간 식별 결과

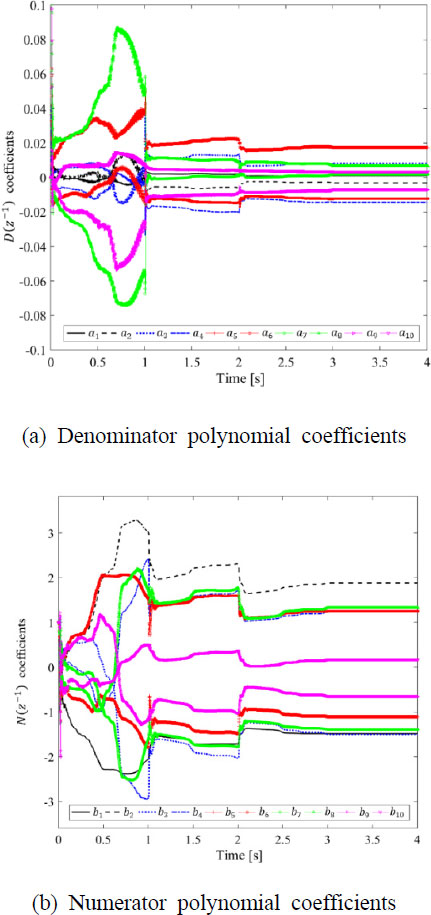
실시간 상태-공간 식별 과정에서 추정된 상태-공간 모델의 정확도는 추정된 전달 함수와 고유진동수의 정확도에 의해 결정된다. Fig. 6(a)와 Fig. 6(b)는 각각 실시간으로 추정된 전달함수의 분모 및 분자 다항식 계수들을 보여준다. Fig. 6(a)와 Fig. 6(b)를 통해, chirp 신호가 목표 주파수 대역을 sweep할 때마다 분모 및 분자 다항식의 계수들이 점차 일정한 값으로 수렴하는 것이 확인된다. Fig. 7은 1000 Hz ~ 1600 Hz에서 0 Hz ~ 600 Hz로 변조된 목표 주파수 대역에서 유한 LRM 평판의 원래 전달함수와 실시간으로 추정된 전달함수의 주파수 응답을 보여준다. Fig. 8은 Fig. 7의 추정된 전달함수로부터 실시간으로 추정된 근의 1, 2, 3, 4, 5번째 고유진동수 f₁, f₂, f₃, f₄, f₅를 보여준다. Table 5는 0 Hz ~ 600 Hz로 변조된 목표 주파수에서 원래 전달함수, 추정된 전달함수, 그리고 추정된 전달함수로부터 추정된 근의 고유진동수를 보여준다. Fig. 7과 Table 5로부터, 1000 Hz ~ 1600 Hz에서 0 Hz ~ 600 Hz로의 주파수 변조 과정에서 원래 전달함수의 4번째 고유진동수 522 Hz의 공진 피크가 작아지는 것이 확인된다. 또한, 주파수 변조 과정에서 100 Hz 미만의 공진 피크가 발생하는 것이 확인된다. 결과적으로, 0 Hz ~ 600 Hz로 변조된 주파수 대역에서 추정된 전달함수는 3, 4, 5번째 고유진동수 186 Hz, 283 Hz, 423 Hz만이 1 %의 상대 오차 범위 내에서 실제 시스템의 고유진동수와 일치하며 원래 전달함수 대비 평균 3.7 dB의 크기 오차 및 각각의 고유진동수에 대해 19도, 35도, 87도의 위상 오차를 갖는다. Fig. 8과 Table 5를 통해, 추정된 전달함수로부터 추정된 근의 1, 3, 4, 5번째 고유진동수 79 Hz, 186 Hz, 284 Hz, 423 Hz는 1 %의 상대 오차 범위 내에서 추정된 전달함수의 1, 3, 4, 5번째 고유진동수와 일치한다. 결과적으로, 추정된 전달함수로부터 추정된 근의 1, 2번째 고유진동수 79 Hz, 130 Hz는 실제 시스템의 고유진동수가 아니라 주파수 변조 및 근찾기 과정에서 발생하는 것으로 제어에 부정적인 영향을 미칠 것으로 예상된다. 추정된 전달함수와 고유진동수로부터 계산된 상태-공간 모델은 Table 6에 나와 있다. 최종적으로, 1000 Hz ~ 1600 Hz의 목표 주파수 대역에서 유한 LRM 평판의 실제 고유진동수 1184 Hz, 1283 Hz, 1417 Hz에 대해 실시간 상태-공간 식별이 잘 수행되었음을 확인했다.

Fig. 6

Real-time estimated transfer function of the finite LRM plate based on RLS filter

Fig. 7

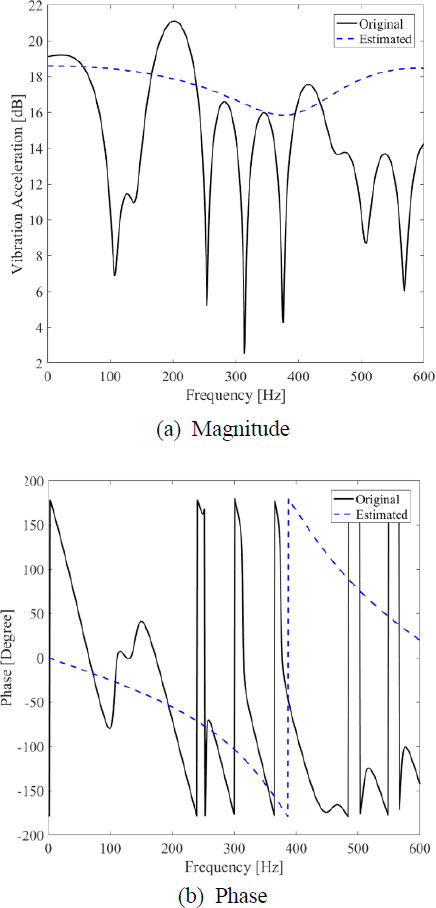
Frequency response of the original and real-time estimated transfer functions of the finite LRM plate

Fig. 8

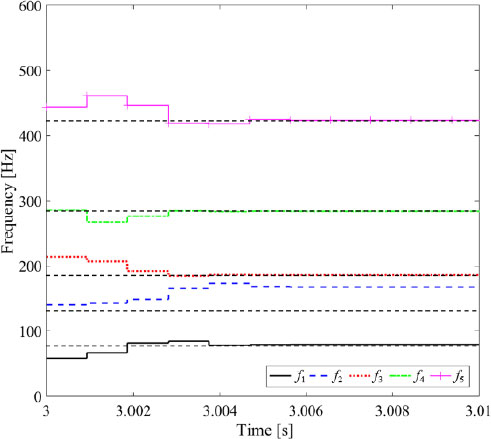
Real-time estimated natural frequencies of the finite LRM plate based on Durand-Kerner method. The horizontal dashed lines indicate the natural frequencies 73 Hz, 130 Hz, 186 Hz, 283 Hz, and 423 Hz from the real-time estimated transfer function in the demodulated target frequency band of 0 Hz ~ 600 Hz

Table 5

Demodulated natural frequencies for the original and estimated transfer functions and estimated roots

Table 6

Real-time estimated state-space model of the finite LRM plate based on partial fraction decomposition

4.2 제어 결과

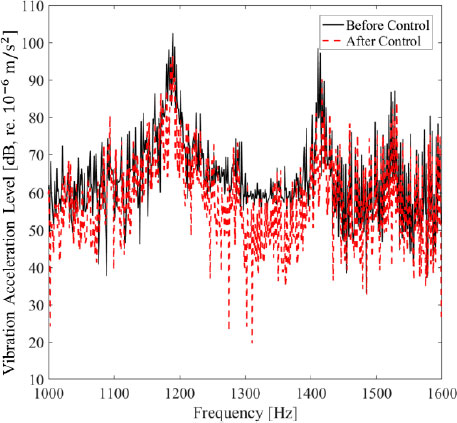
Fig. 9는 외란 액추에이터에 랜덤 신호가 인가됐을 때 제어 전후 가속도 신호의 시간 응답을 보여준다. Fig. 9를 통해, 제어가 시작되는 20 s 이후 가속도 응답이 감소되는 것이 확인된다. Table 7에서 보여졌듯이, 제어 후 가속도 응답은 1000 Hz ~ 1600 Hz의 주파수 대역에서 총 6.7 dB 감소한다. Kim 등⁽⁹⁾의 연구에서, LRM을 단독으로 사용할 경우 763 Hz ~ 1614 Hz의 목표 주파수 대역에서 가속도 응답은 총 22.9 dB 감소한다. 따라서, LRM과 AVC를 동시에 사용할 경우 763 Hz ~ 1614 Hz의 목표 주파수 대역에서 총 29.6 dB의 가속도 응답 감소가 기대된다. Fig. 10은 제어 전후 가속도 신호의 주파수 응답을 보여준다. Fig. 10을 통해, 가장 큰 피크 값과 대역폭을 갖는 공진 주파수 1184 Hz와 1417 Hz에서 각각 6.1 dB와 8.5 dB의 가속도 응답 감소가 확인된다. 반면, 제어 후 1100 Hz 근방에서의 가속도 응답 증가는 Section 4.1에서 언급되었듯이 근찾기 과정에서 발생하는 1130 Hz의 가상 고유진동수로 인한 것이다. 또한, 제어 후 1500 Hz ~ 1600 Hz에서 가속도 응답 감소가 관측되지 않는 것은 Section 4.1에서 언급되었듯이 주파수 변조 과정에서 발생하는 전달함수 추정 오차로 인해 1522 Hz의 고유진동수가 추정되지 못했기 때문이다. Fig. 9, Fig. 10과 Table 7로부터, 실시간 상태-공간 식별 기반 AVC를 통해 유한 LRM 평판의 목표 주파수 대역에서 발생하는 임의의 진동모드 저감이 가능함을 확인했다.

Fig. 9

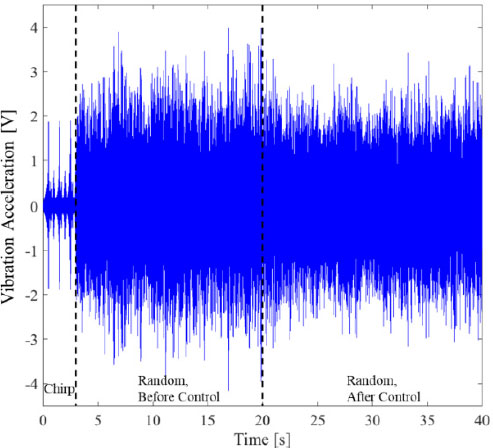
Time response of vibration acceleration during AVC when a random disturbance is applied to the finite LRM plate

Table 7

Comparison of vibration acceleration levels in 1000 Hz ~ 1600 Hz before and after control

Fig. 10

Frequency response of vibration acceleration during AVC when a random disturbance is applied to the finite LRM plate

5. 결 론

이 연구에서는, 유한 LRM 평판의 목표 주파수 대역에서 발생하는 임의의 진동모드를 저감하기 위한 실시간 상태-공간 식별 기반 AVC 방법이 제안되었다. 제안된 방법이 적용된 AVC 시스템은 상태-되먹임 제어를 위한 상태-공간 모델의 추정을 위해 실시간 상태-공간 식별 과정이 수행된다. 실시간 상태-공간 식별 과정은 RLS 필터에 기반한 전달함수의 추정, Durand-Kerner 방법에 기반한 고유진동수의 추정과 부분분수분해에 기반한 상태-공간 모델 계산으로 구성된다. 이 연구에서 제안된 AVC 방법은 COMSOL에 기반한 유한요소 모델과 Simulink에 기반한 시뮬레이션을 통해 검증이 수행되었다. 유한 LRM 평판의 실시간 상태-공간 식별 결과는 목표 주파수 대역에서 발생하는 진동모드의 전달함수, 고유진동수와 상태-공간 모델이 잘 추정되었음을 보여줬다. 실시간으로 추정된 상태-공간 모델에 기반한 상태-되먹임 제어 결과는 랜덤 외란에 대해 1000 Hz ~ 1600 Hz의 주파수 대역에서 총 6.7 dB, 공진 주파수 1184 Hz와 1417 Hz에서 각각 6.1 dB와 8.5 dB의 가속도 응답 감소를 보여줬다. 이 연구에서 제안된 AVC 방법은 기존의 수동적 진동 저감 방법과 결합하여 변동하는 시스템의 랜덤 외란에 대한 진동을 효과적으로 감소시키는 데 활용될 수 있다.

Acknowledgments

이 연구는 한화시스템의 지원을 받아 작성되었습니다.

References

• Huang, H. B., Wu, J. H., Huang, X. R., Yang, M. L. and Ding, W. P., 2019, The Development of a Deep Neural Network and Its Application to Evaluating the Interior Sound Quality of Pure Electric Vehicles, Mechanical Systems and Signal Processing, Vol. 120, pp. 98~116. [https://doi.org/10.1016/j.ymssp.2018.09.035]
• Jung, B. C., Lee, D., Youn, B. D. and Lee, S., 2011, A Statistical Characterization Method for Damping Material Properties and Its Application to Structural-acoustic System Design, Journal of Mechanical Science and Technology, Vol. 25, No. 8, pp. 1893~1904. [https://doi.org/10.1007/s12206-011-0517-6]
• Kim, H. G., Nerse, C. and Wang, S., 2019, Topography Optimization of an Enclosure Panel for Low-frequency Noise and Vibration Reduction using the Equivalent Radiated Power Approach, Materials and Design, Vol. 183, p. 108125. [https://doi.org/10.1016/j.matdes.2019.108125]
• Sangiuliano, L., Claeys, C., Deckers, E. and Desmet, W., 2020, Influence of Boundary Conditions on the Stop Band Effect in Finite Locally Resonant Metamaterial Beams, Journal of Sound and Vibration, Vol. 473, p. 115225. [https://doi.org/10.1016/j.jsv.2020.115225]
• Lu, M. H., Feng, L. and Chen, Y. F., 2009, Phononic Crystals and Acoustic Metamaterials, Materials Today, Vol. 12, No. 12, pp. 34~42. [https://doi.org/10.1016/S1369-7021(09)70315-3]
• Sánchez-Pérez, J. V., Caballero, D., Mártinez-Sala, R., Rubio, C., Sánchez-Dehesa, J., Meseguer, F., Llinares, J. and Gálvez, F., 1998, Sound Attenuation by a Two-dimensional Array of Rigid Cylinders, Physical Review Letters, Vol. 80, No. 24, p. 5325. [https://doi.org/10.1103/PhysRevLett.80.5325]
• Goffaux, C., Maseri, F., Vasseur, J. O., Djafari-Rouhani, B. and Lambin, P., 2003, Measurements and Calculations of the Sound Attenuation by a Phononic Band Gap Structure Suitable for an Insulating Partition Application, Applied Physics Letters, Vol. 83, No. 2, pp. 281~283. [https://doi.org/10.1063/1.1592016]
• Deymier, P. A. (Ed.), 2013, Acoustic Metamaterials and Phononic Crystals, Vol. 173, Springer Science and Business Media. [https://doi.org/10.1007/978-3-642-31232-8]
• Kim, H. G., Jeon, O. and Wang, S., 2021, A Numerical and Experimental Study on an Interconnected Metamaterial for Flexural Vibration Control Based on Modal Strain Energy, Applied Sciences, Vol. 11. No. 10, p. 4530. [https://doi.org/10.3390/app11104530]
• Yu, J., Nerse, C., Chang, K. J. and Wang, S., 2021, A Framework of Flexible Locally Resonant Metamaterials for Attachment to Curved Structures, International Journal of Mechanical Sciences, Vol. 204, p. 106533. [https://doi.org/10.1016/j.ijmecsci.2021.106533]
• Rew, K. H., Han, J. H. and Lee, I., 2002, Multi-modal Vibration Control using Adaptive Positive Position Feedback, Journal of Intelligent Material Systems and Structures, Vol. 13, No. 1, pp. 13~22. [https://doi.org/10.1177/1045389X02013001866]
• Zhang, T., Li, H. G. and Cai, G. P., 2013, Hysteresis Identification and Adaptive Vibration Control for a Smart Cantilever Beam by a Piezoelectric Actuator, Sensors and Actuators A: Physical, Vol. 203, pp. 168~175. [https://doi.org/10.1016/j.sna.2013.08.042]
• Zhang, T., Li, H. G., Zhong, Z. Y. and Cai, G. P., 2015, Hysteresis Model and Adaptive Vibration Suppression for a Smart Beam with Time Delay, Journal of Sound and Vibration, Vol. 358, pp. 35~47. [https://doi.org/10.1016/j.jsv.2015.08.017]
• Krenk, S. and Høgsberg, J., 2009, Optimal Resonant Control of Flexible Structures, Journal of Sound and Vibration, Vol. 323, No. 3-5, pp. 530~554. [https://doi.org/10.1016/j.jsv.2009.01.031]
• Han, J. H., Rew, K. H. and Lee, I., 1997, An Experimental Study of Active Vibration Control of Composite Structures with a Piezo-ceramic Actuator and a Piezo-film Sensor, Smart Materials and Structures, Vol. 6, No. 5, p. 549. [https://doi.org/10.1088/0964-1726/6/5/006]
• Nestorović, T., Durrani, N. and Trajkov, M., 2012, Experimental Model Identification and Vibration Control of a Smart Cantilever Beam using Piezoelectric Actuators and Sensors, Journal of Electroceramics, Vol. 29, No. 1, 42~55. [https://doi.org/10.1007/s10832-012-9736-1]
• Jeon, O., Ryu, H., Kim, H. G. and Wang, S., 2020, Vibration Localization Prediction and Optimal Exciter Placement for Improving the Sound Field Optimization Performance of Multi-channel Distributed Mode Loudspeakers, Journal of Sound and Vibration, Vol. 481, p. 115424. [https://doi.org/10.1016/j.jsv.2020.115424]
• Haykin, S. S., 2014, Adaptive Filter Theory (5th ed.), Pearson Education.
• Aberth, O., 1973, Iteration Methods for Finding All Zeros of a Polynomial Simultaneously, Mathematics of Computation, Vol. 27, No. 122, pp 339~344. [https://doi.org/10.1090/S0025-5718-1973-0329236-7]
• Ehrlich, L. W., 1967, Modified Newton Method for Polynomials, Communications of the ACM, Vol. 10, No. 2, pp. 107~108. [https://doi.org/10.1145/363067.363115]
• Jeon, O., Kim, H. G., Kook, J., Kim, S. and Wang, S., 2022, Active Structural Acoustic Control for Radiated Sound Power Reduction of Enclosure with Vent Holes based on Radiation Modes, Journal of Mechanical Science and Technology, Vol. 36, No. 7, pp. 3313~3327. [https://doi.org/10.1007/s12206-022-0611-y]
• MIQUEL, Thierry. State space modelling. Master, ENAC, France,⟨ hal-02987750v2, 2021.
• Mathews, J. and Howell, R., 2012, Complex Analysis for Mathematics and Engineering. Jones and Bartlett Publishers.
• Michau, M., Micheau, P., Boulandet, R., Berry, A. and Herzog, P., 2014, Decentralized Complex Envelope Controller for ASAC by Virtual Mechanical Impedances, IEEE/ASME International Conference on Advanced Intelligent Mechatronics, pp. 162~167. [https://doi.org/10.1109/AIM.2014.6878072]