앵커기초의 균열을 고려한 모형 전기 캐비닛의 지진거동특성 분석을 위한 진동대실험

1. 서 론

원자력 발전소의 안전성 확보를 위해 안전관련기기의 성능검증은 무엇보다 중요하다. 안전관련기기의 손상은 방사능의 유출과 관련된 중대사고의 원인이 될 수 있다. 그러므로 안전관련기기의 사용기간 동안 발생할 수 있는 다양한 하중조건에 대한 성능검증을 수행하여 주요기능의 정상작동을 확인할 필요가 있다⁽¹⁾. 이러한 안전관련기기에 작용하는 다양한 환경하중으로 자연노화, 방사선노화, 열적노화, 진동, 마모 등이 있다. 국내 원자력 발전소들은 다양한 환경하중을 고려한 안전관련기기들의 성능검증을 수행하여 현장에 적용한다. 특히 원자로 시설은 주기적으로 안전성평가를 실시해야 하며 설계수명기간이 만료되는 경우에는 가동정지 또는 기간 연장의 선택을 위한 안전성평가를 실시해야한다⁽²⁾. 따라서 기기의 성능에 대한 재평가가 요구될 수 있으므로 열화에 의한 성능저하 수준을 검토할 필요가 있다.

1980년대 미국에서는 원자력 발전소의 열화기기들의 내진성능 평가를 위한 실험적 연구들이 수행되었다^(3,4). 그러나 열화에 따른 성능저하 평가 내용은 많지 않으며 일반적인 설계수명보다 짧은 노화기간으로 연구가 수행되었으므로 직접적인 참고에는 한계가 있다. 최근 국내에서는 수력발전소 설비 중에서 설계수명이 종료된 열화기기들을 대상으로 내진성능 평가를 위한 진동대실험이 수행되기도 하였다^(5,6). 그러나 원전기기와 달리 초기 조건에 대한 내진성능평가 자료의 부재로 열화에 따른 성능저하 평가는 어려울 수 있다.

원자력 발전소의 안전관련기기들의 지진안전성 평가를 위한 연구는 지속적으로 수행되고 있으며 특히 전기 캐비닛의 거동특성 분석 및 내부응답을 예측하기 위한 연구들이 진행되고 있다^(7~10). EPRI(Electric Power Research Institute)는 캐비닛 내부응답스펙트럼(ICRS, in-cabinet response spectrum)을 계산하는 간편법과 정밀해석법을 제시하고 있다⁽¹¹⁾. 일반적으로 캐비닛모델 바닥의 경계조건은 모든 자유도에 대하여 구속된 것으로 가정하지만 실제 바닥의 경계조건은 가정된 구속 조건과 다르다. 캐비닛이 앵커볼트로 정착된 경우 앵커 주변 판재 변형에 의한 들림(uplifting)과 로킹(rocking)으로 인한 충격이 발생하게 된다. 발생된 충격은 캐비닛에 다양한 변수로 작용하게 되므로 로킹의 영향을 고려하기 위한 연구가 수행된 바 있다^(12~14). 그러나 수치해석으로 캐비닛에 발생하는 충격을 모사하는 것은 한계가 있어 전기 캐비닛의 앵커부 및 기초를 현장조건과 동일하게 구성한 진동대실험이 수행되기도 하였다⁽¹⁵⁾.

열화된 전기 캐비닛의 내진성능 분석을 위하여 방사선노화, 열적노화 등의 모사는 현실적으로 제한적일 수 있다. 또한 원자력 발전소 현장에서 사용 중인 전기 캐비닛의 내부 부품들의 상세한 조사에는 한계가 있다. 반면에 전기 캐비닛이 고정된 콘크리트 기초의 균열은 육안으로 현장조사가 가능하며 실험적으로 모사가 가능한 대표적인 열화이다.

이 연구에서는 콘크리트 기초의 균열을 열화 조건으로 고려하고 앵커볼트로 고정된 모형 전기 캐비닛의 지진거동특성을 분석하기 위하여 진동대실험을 수행하였다. 균열을 모사한 콘크리트 기초와 앵커볼트는 현장조사결과 및 앵커실험에 대한 규격을 참조하여 제작하였다. 모형 전기 캐비닛의 설계를 위하여 원자력 발전소에서 사용되는 캐비닛의 제원 및 현장조사로 계측된 공진주파수 결과를 참조하였다. 유한요소해석 결과를 바탕으로 모형 전기 캐비닛을 제작하였다. 진동대실험을 수행하고 모형 전기 캐비닛의 지진하중에 의한 파손 및 가속도 응답에 따른 지진거동특성을 확인하였다. 또한 균열을 열화 조건으로 고려하였으므로 균열 유·무에 따른 모형 전기 캐비닛의 거동을 분석 및 비교하였다.

2. 실험 시료 구성

2.1 앵커기초의 설계 및 제작

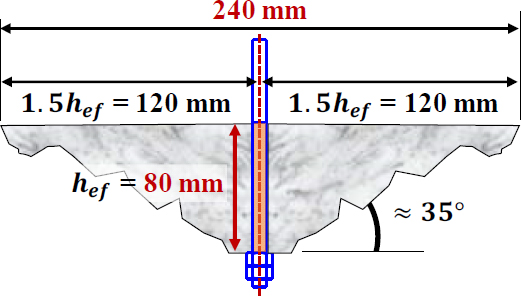
앵커볼트로 구성된 기초의 가장 대표적인 열화는 콘크리트의 균열이다. 이 연구에서는 원자력 발전소의 현장조사결과와 앵커기초에 대한 설계규격을 참조하여 균열이 포함된 콘크리트 기초 및 앵커볼트를 제작하였다. 콘크리트 기초는 원자력 발전소 구조물의 설계 및 실험 여건을 고려하여 27 MPa의 강도와 150 mm의 두께로 설정하였다. ACI 355.2⁽¹⁶⁾의 Table 4.2에서 균열 콘크리트에 사용할 앵커 시스템 평가 시 지진 인장 및 전단의 경우 0.5 mm의 균열폭으로 규정하고 있다. 따라서 열화 고려를 위한 균열은 ACI 355.2 및 현장조사결과에 따라 0.5 mm로 설정하였다. 앵커볼트의 매입 깊이는 콘크리트 기초 두께를 고려하여 80 mm로 설정하였다. 매립된 앵커볼트의 인발하중에 의한 콘크리트의 파괴단면은 Fig. 1에 나타내었다. Fig. 1에서 인발에 의한 파괴단면의 직경은 240 mm로 산정된다. 따라서 인발에 의한 파괴단면을 초과하도록 균열의 길이를 260 mm로 설정하였다. 균열의 모사는 그리스가 도포된 얇은 스테인리스 박판을 이용하여 모사하는 방법을 적용하였다⁽¹⁷⁾.

Fig. 1

Pullout failure cross-section of concrete

이 방법은 정의된 균열의 제원에 따라 스테인리스 박판을 적용하므로 균열 제작의 변수를 최소화할 수 있으며 실험 중 지진동에 의한 기초의 쪼개짐 등을 예방할 수 있다.

원자력 발전소의 현장조사결과 대부분 전기 캐비닛 1기에 대하여 4 ~ 8개의 M10 또는 M12 규격의 앵커볼트가 사용되고 있는 것을 확인하였다. 이 연구에서는 독립된 전기 캐비닛의 취약 조건의 구성을 위하여 M10 규격의 4개의 앵커볼트로 고정되는 것으로 가정하였다. 앵커볼트는 ASTM A36 규격으로 제작되었으며 Fig. 2에 나타내었다. 콘크리트 타설 전 기초에 미리 앵커볼트를 설치하여 콘크리트와 일체가 되도록 하는 선 설치 앵커방식으로 제작하였다.

Fig. 2

M10 anchor bolt

2.2 모형 전기 캐비닛의 설계 및 제작

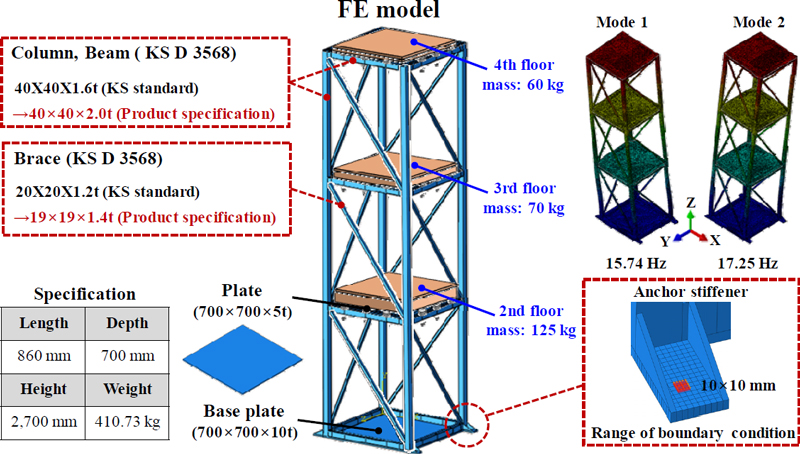
원자력 발전소에서 설치되어 있는 실제 기기의 반출은 현실적으로 많은 제한이 따른다. 이 연구에서는 현장조사결과를 참조하여 17 Hz의 목표 고유진동수로 하는 모형 전기 캐비닛을 설계하였다. 설계를 위하여 유한요소해석 프로그램(ABAQUS Ver.6.12)을 이용하여 모형 전기 캐비닛의 유한요소모델을 작성하였다. 실험의 변수를 최소화하기 위하여 캐비닛을 구성하는 프레임은 모두 솔리드(solid) 요소로 작성하였다. 실제 제작 시 모든 프레임을 용접 연결하기 위하여 해당 부재를 모두 병합(merge)하여 하나의 모델(part)로서 작성하였다. 기둥, 보, 사재로 구성되는 부재는 각관으로 구성하였으며 KS D 3568에 따라 적절한 제원을 결정하였다. 바닥 판재의 두께는 10 mm이며 앵커부의 경계조건은 제작된 앵커볼트의 직경을 고려하였다. 각 층을 구성하는 두께 5 mm의 판재에 비구조 질량을 정의하여 실험 시 사용될 모형 질량체를 모사하였다. 목표 고유진동수의 동특성을 가지는 모델을 선정하고자 모형 질량체의 높이 및 무게 등을 적절히 변경하며 고유치해석을 수행하였다. 선정된 유한요소모델을 Fig. 3에 나타내었다. 제작될 앵커기초의 형상과 보강재(stiffener) 활용 및 고정면적 등의 변수에 따라 약축(Y)과 강축(X)의 고유진동수를 다르게 설계하였다. 설계 모델에 대한 전체 하중은 410.73 kg이다. 1차 및 2차 모드의 고유진동수는 각각 15.74 Hz와 17.25 Hz이며 각 모드의 병진 및 회전에 대한 모드참여계수를 Table 1에 나타내었다. 설계 모델과 동일하게 진동대실험을 위한 모형 전기 캐비닛을 제작하였다.

Fig. 3

Finite element model of mock-up electrical cabinet and mode shapes

Table 1

Modal participation factor

3. 진동대실험 개요

3.1 실험 구성

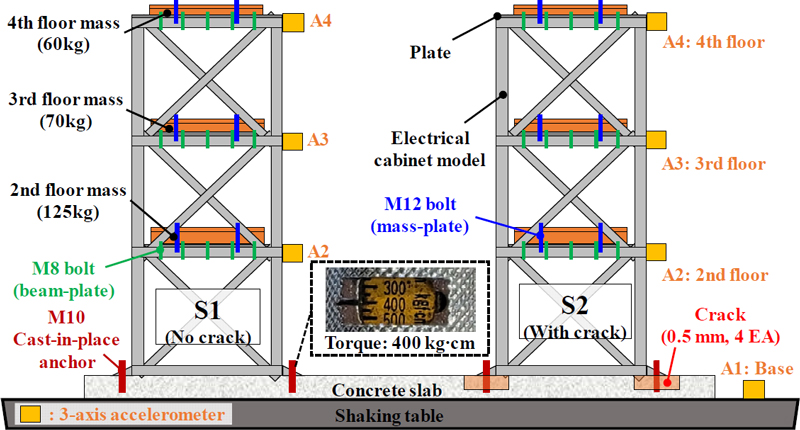
모형 전기 캐비닛의 진동대실험을 위한 구성을 Fig. 4에 나타내었다. 용접 연결된 프레임과 각 층을 구성하기 위한 판재는 16개의 M8 볼트로 고정하였다. 각 층의 하중 적용을 위해 판재와 모형 질량체는 6개의 M12 볼트로 고정하였다. 콘크리트 기초에 선 설치된 M10 앵커볼트와 모형 전기 캐비닛은 토크렌치를 이용하여 400 kgf·cm의 동일한 체결력으로 지지부를 구성하였다⁽¹⁸⁾. 이 연구에서 앵커기초에 균열이 없는 모형 전기 캐비닛을 S1, 0.5 mm의 균열이 고려된 모형 전기 캐비닛을 S2로 정의하였다. 동일한 입력지진동에 대한 S1과 S2의 응답을 확인하고자 콘크리트 기초에 함께 설치하였다. 모형 전기 캐비닛의 각 층에 3축 가속도 센서(PCB 356A16)를 부착하여 지진거동특성을 분석하기 위한 가속도 응답을 계측하였다. 또한 입력가속도 위치에 대한 각 층의 가속도 응답의 전달함수 산정을 위하여 진동대 바닥에 3축 가속도 센서를 부착하였다.

Fig. 4

Shake table test set-up

3.2 입력 지진동

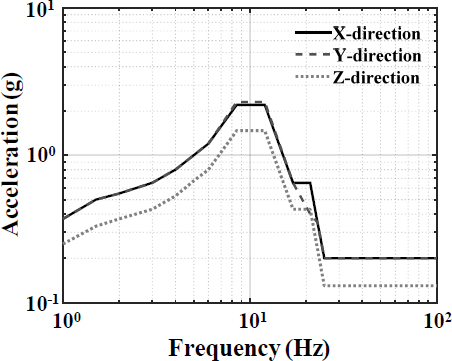
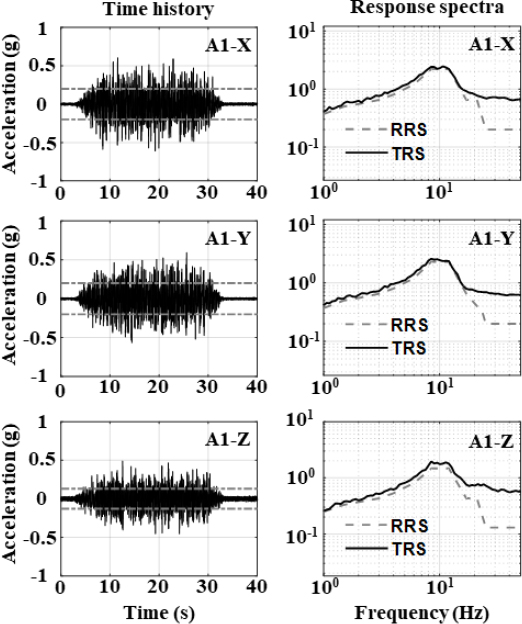
지진모사실험(seismic simulation test)을 위한 요구응답스펙트럼(RRS, required response spectrum)을 Fig. 5에 나타내었다. 고리1호기 최종 안전성평가 분석보고서에 제시된 보조건물 12.192 m와 21.336 m 층응답스펙트럼에 기반하여 생성하였으며 감쇠비는 5 %이다. 고리1호기 설계지진의 수평방향 설계응답스펙트럼은 1940년 El Centro 응답스펙트럼을 따르며 수직방향 성분은 모든 진동수에 대하여 수평방향 성분의 2/3이다. 요구응답스펙트럼의 수평 및 수직방향에 대한 최대 지반가속도는 각각 0.2 g 및 0.14 g이다. 이 연구에서 사용된 진동대는 부산대학교 지진방재연구센터에서 운용 중인 6 자유도 진동대를 사용하였다. 진동대의 성능을 고려하고 IEEE 344⁽¹⁹⁾를 참조하여 가속도시간이력을 작성하였다. 작성된 가속도시간이력은 1 Hz ~ 50 Hz의 주파수 범위로 진동지속시간 30초, 강진지속시간 20초, 상호상관함수는 0.3 이하이다. 작성된 가속도시간이력과 가속도시간이력에 대한 실험응답스펙트럼(TRS, test response spectrum)을 Fig. 6에 나타내었다. 가속도시간이력 그래프에서 회색 점선은 영주기가속도(ZPA, zero period acceleration)의 90 %를 나타낸 것이다. 응답스펙트럼 그래프에서 검은색 실선은 가속도시간이력에 대한 TRS로서 RRS의 포락 여부를 확인하며 실험을 진행하였다.

Fig. 5

Required response spectrum

Fig. 6

Acceleration times histories and TRS

3.3 실험 절차 및 방법

진동대실험의 절차 및 방법을 Table 2에 나타내었다. 지진모사실험 수행 전 모형 전기 캐비닛의 육안검사 및 공진탐색실험(resonance search test)을 수행하였다. 이후 지진모사실험을 수행한 후 모형 전기 캐비닛의 동특성 변화 및 건전성 확인을 위하여 공진탐색실험과 육안검사의 순서로 실험을 진행하였다. 여기서 공진탐색실험을 위한 실효값(RMS, root mean square)으로 0.1 g의 불규칙파(random wave)를 이용하여 수평(X, Y) 및 수직(Z) 방향 각각에 대하여 독립적으로 수행하였다. 0.5 Hz ~ 50 Hz의 주파수 범위로 진동지속시간은 60초 이상 가진하였다. 지진모사실험은 Fig. 5의 RRS를 이용하여 작성한 가속도 시간이력을 입력지진동으로 3축 동시 가진에 의한 진동대실험을 수행하였다. 앵커부 및 가속도 응답을 확인하며 요구응답스펙트럼의 100 %, 200 %, 250 %, 300 %의 크기로 가속도 배율을 증가시키며 진행하였다. Table 2의 절차를 반복 수행하였으며 캐비닛의 손상으로 실험을 종료하였다.

Table 2

Test procedure and method

4. 실험결과 분석

4.1 육안검사 및 공진탐색실험 결과

Table 3은 육안검사 및 공진탐색실험 결과를 나타내었다. 이 논문에서 실험명의 간소화를 위해 공진탐색실험을 RES, 지진모사실험은 EQ로 정의하였다. 육안검사 결과는 각 EQ 수행 후 시료의 상태를 나타낸 것이다.

Table 3

Resonance search test results

공진주파수는 식 (1)과 같이 입력된 가속도 위치에 대한 각 계측위치에서 가속도 응답의 전달함수(T_ab)를 산정함으로써 결정하였다.

$\[ T_{ab}\left(f\right)= \]$

(1)

여기서 P_aa는 입력된 신호의 파워 스펙트럼 밀도(PSD, power spectral density)이고 P_ba는 입력신호와 출력신호의 상호 파워 스펙트럼 밀도(CSD, cross power spectral density)이다. 수직 방향에 대한 공진주파수는 모두 40.50 Hz로 표에서 생략하였다.

S1의 공진주파수 변화는 0.25 Hz, S2의 공진주파수의 변화는 0.25 Hz ~ 0.50 Hz로 나타났으며 이는 실험 오차 수준으로 판단하였다. Fig. 7과 같이 EQ5 수행 중 S1의 앵커볼트 파손으로 실험의 절차는 종료되었다. 공진탐색실험 결과 시료에 파손이 발생할 때까지 구조적인 변화는 크지 않으며 지지부의 강성 변화에는 큰 차이가 없는 것으로 판단하였다. 실험결과 지진하중에 의한 모형 전기 캐비닛의 파손은 앵커볼트의 파손으로 확인하였으며 S1의 앵커볼트가 더 낮은 가진력에서 파손되는 것을 확인하였다.

Fig. 7

Failure mode of electrical cabinet model

4.2 지진모사실험 결과

지진하중이 발생하면 캐비닛의 앵커볼트 주변에서 국부변형이 발생할 수 있으며 앵커볼트 주변을 제외한 캐비닛 하부에서 들림 현상이 발생할 수 있다. 이러한 들림 현상은 캐비닛 하부 모서리의 강체회전(rigid body rotation)으로 인한 로킹 현상이 발생하며 캐비닛의 하부 및 앵커부는 바닥과 충돌하여 캐비닛의 가속도 응답을 증폭시킬 수 있다⁽¹²⁾. 따라서 가속도 응답의 최대값으로 캐비닛의 지진거동을 비교하는 것은 부적절할 수 있다. IEEE std 693⁽²⁰⁾에서 ZPA는 RRS 범위 이상의 고주파영역의 가속도 값으로써 최대 가속도 값을 나타낸다. 이 연구에서는 RRS에서 가장 높은 주파수 및 진동대의 성능을 고려한 ZPA를 정의함으로써 지진거동특성을 분석하고자 하였다. 따라서 진동대의 성능과 TRS의 octave 등을 고려하여 TRS에서 45.25 Hz의 스펙트럼 가속도 값을 ZPA로 정의하였다.

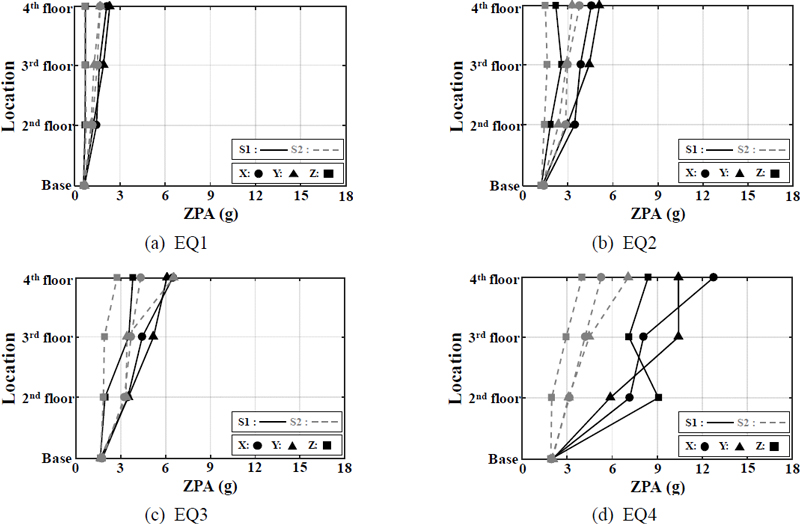
Fig. 8 및 Table 4에 시료의 각 층의 위치에 따른 TRS에 대한 ZPA 값을 정리하였다. EQ1에서 2층의 수직 방향을 제외하고 모두 S1의 ZPA의 값이 크게 나타났다.

Fig. 8

ZPA by the location of electrical cabinet model

Table 4

ZPA (spectral acceleration at 45.25 Hz in TRS)

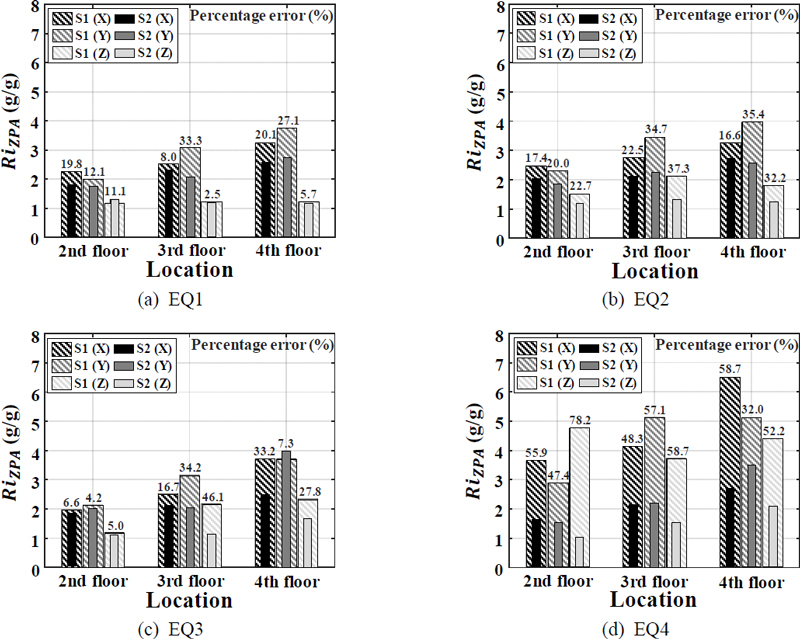
Fig. 8의 검은색 실선은 균열이 없는 S1이며 회색 점선은 균열을 고려한 S2이다. EQ의 가진력이 커질수록 ZPA의 편차가 증가한다. Fig. 8(d)와 같이 EQ4에서 S1의 ZPA 값이 크게 증가하며 더 큰 편차를 나타내었다. S2보다 S1에서 앞서 언급한 로킹 현상 및 충격 등이 더 크게 발생하며 가속도 응답이 증폭된 것으로 판단하였다. 따라서 실험이 진행됨에 따라 S2보다 S1의 앵커볼트에서 더 큰 충격 및 손상이 지속적으로 누적됨에 따라 가속도 응답의 편차는 더 크게 나타났으며 그 결과 앵커볼트가 파손된 것으로 판단하였다. 진동대 바닥에서 계측된 가속도 응답에 대한 시료의 해당 위치에서 계측된 가속도 응답의 비를 이용하여 가속도 증폭을 검토할 수도 있다. Fig. 9 및 Table 5는 식 (2)에 의해 계산된 진동대 바닥(A1)에 대한 각 층(Ai)에서의 ZPA 값의 비를 나타내었다. 대부분의 EQ에서 두 시료에 대한 ZPA 비의 최대값은 최상층인 4층에서 나타난다. 각 EQ에서 S1의 ZPA 비의 최대값은 S2에 비해 대부분 크다.

Fig. 9

ZPA ratio by the location of electrical cabinet model

Table 5

ZPA ratio to base

$\[ R{i}_{ZPA}=\frac{A{i}_{ZPA}\left(\mathrm{C}\mathrm{o}\mathrm{m}\mathrm{p}\mathrm{o}\mathrm{n}\mathrm{e}\mathrm{n}\mathrm{t}\right)}{A{1}_{ZPA}\left(\mathrm{G}\mathrm{r}\mathrm{o}\mathrm{u}\mathrm{n}\mathrm{d}\right)} \]$

(2)

Fig. 9(a)에서 2층의 수직 방향(Z)과 Fig. 9(c)에서 4층의 수평 방향(Y)을 제외하고 모두 S1이 크다. Fig. 9(d)와 같이 ZPA 비의 편차는 최소 32.0 %에서 최대 78.2 %로 EQ4에서 더 큰 것을 확인할 수 있다. 이 연구에서 모형 전기 캐비닛의 앵커볼트 파손 및 가속도 응답에 대한 실험결과는 결과적으로 균열이 없는 앵커기초 조건에서 내진성능 저하가 발생한 것과 유사한 결과를 나타내었다. 최근 기존 앵커 시스템에 탄성 중합체의 링(elastomeric ring)을 적용하여 저손상 앵커 시스템을 제안한 연구가 수행된 바 있다⁽²¹⁾. 이 연구에서 제안된 저손상 앵커 시스템의 성능을 실험적으로 평가하기 위하여 균열이 없는 콘크리트 기초와 가진방향과 평행하게 0.5 mm의 균열폭이 적용된 콘크리트 기초를 대상으로 진동대실험을 수행하였다. 가속도 응답 및 앵커 하중을 기존 앵커 시스템과 비교한 결과 저손상 앵커 시스템의 성능은 균열이 없는 조건보다 균열을 고려한 조건일 때 더 우수하였으며 응답의 감소량이 더 크게 증가하였다. 연구의 결과로 균열 조건에서 연결(connection)의 유연성(flexibility)과 이력(hysteresis) 현상에 따라 면진(isolation) 및 소산(dissipation) 작용을 하며 추가적으로 이력 감쇠(hysteretic damping)를 통하여 가속도 응답 및 앵커 고정력의 감소를 확인하였다. 따라서 이 연구에서 고려한 0.5 mm의 균열폭은 이와 유사하게 작용하여 S2의 가속도 응답을 감소시켰으며 균열이 없는 S1의 앵커볼트가 더 낮은 가진력에서 파손된 것으로 판단하였다.

5. 결 론

이 연구에서는 원자력 발전소의 안전관련기기들 중 전기 캐비닛을 대상으로 열화를 고려한 지진성능을 확인 및 비교하고자 하였다. 고리 1호기의 현장조사결과를 바탕으로 모형 전기 캐비닛과 앵커기초를 설계 및 제작하고 균열을 열화 조건으로 고려하여 진동대실험을 수행하였다. 실험결과로부터 균열 유·무에 따른 모형 전기 캐비닛의 지진거동특성을 분석하였다.

지진하중 하에서 모형 전기 캐비닛의 파손은 앵커볼트의 파손으로 확인하였다. 앵커볼트의 파손은 앵커기초에 균열이 없는 S1이 균열을 고려한 S2보다 더 낮은 가진력에서 발생하였다. EQ 수행에 따라 가속도 응답으로부터 정의된 ZPA의 값은 대부분 S1에서 크게 나타났다. 또한 EQ의 가진력이 커질수록 S2에 비해 S1의 ZPA의 값은 더 커지며 편차가 증가하였다. 진동대 바닥에 대한 각 층에서의 ZPA 비는 두 시료 모두 최상층에서 최대값이 나타났으며 대부분 S1이 S2보다 큰 값을 나타내었다. 균열이 없는 S1 시료에서 내진성능 저하가 발생한 것과 유사한 결과를 나타내었다. 더 큰 충격의 발생과 함께 가속도 증폭의 경향이 더 클 수 있어 더 낮은 지진하중에서도 앵커볼트가 파손될 가능성이 있는 것으로 판단하였다. 따라서 이 연구에서 열화 조건으로 고려한 앵커기초의 0.5 mm 폭의 균열은 모형 전기 캐비닛의 내진성능 저하의 영향이 작은 것으로 판단된다. 그러나 이 연구에서 고려한 열화 조건은 균열에 대한 하나의 매개변수로서 제한적이다. 균열 폭, 콘크리트 강도 등과 같은 앵커기초의 다양한 매개변수를 고려하고 신뢰성있는 실험 결과 확보를 위하여 추가적인 실험적 연구가 필요할 것으로 판단된다.

Acknowledgments

이 연구는 산업통상자원부와(MOTIE)와 한국에너지기술평가원(KETEP)의 지원을 받아 수행한 연구과제입니다(과제번호 20217910100150).

References

• The Institute of Electrical and Electronics Engineers (IEEE), 2004, IEEE Standard for Qualifying Class 1E Equipment for Nuclear Power Generating Stations, IEEE Std 323-2003.
• Nuclear Safety and Security Commission (NSSC), 2021, Article 36(Timing for Periodic Safety Reviews), The Enforcement Decree of the Nuclear Safety Act.
• Bonzon, L. L., Hente D. B., Kukreti, B. M., Schendel, J. S., Tulk, J. D., Janis, W. J., Black, D. A., Paulsen, G. D. and Aucoin, B. D., 1984, Test Series 1: Seismic-fragility Tests of Naturally-aged Class 1E Gould NCX-2250 Battery Cells, Technical Report No. NUREG/CR-3923, SAND-84-1737. [https://doi.org/10.2172/6060342]
• Bonzon, L. L., Janis, W. J., Black, D. A. and Paulsen, G. A., 1987, Seismic-fragility Tests of New and Accelerated-aged Class 1E Battery Cells, Technical Report No. NUREG/CR-4098, SAND-84-2631. [https://doi.org/10.2172/6518144]
• Jeon, B.-G., Yun, D.-W., Shin, Y.-J. and Jung, W.-Y., 2019, Seismic Performance Evaluation for Hydroelectric Power Plants RTU Panel by Shaking Table Tests, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 6, pp. 770~779. [https://doi.org/10.5050/KSNVE.2019.29.6.770]
• Lee, S.-M., Jeon, B.-G., Yun, D.-W., Kim, S.-W. and Jung, W.-Y., 2020, Seismic Response Characteristics of Used Molded Transformer Anchored on Concrete Slab, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 30, No. 6, pp. 624~633. [https://doi.org/10.5050/KSNVE.2020.30.6.624]
• Merz, K. L. and Ibanez, P., 1990, Guidelines for Estimation of Cabinet Dynamic Amplification, Nuclear Engineering and Design, Vol. 123, No. 2-3, pp. 247~255. [https://doi.org/10.1016/0029-5493(90)90244-R]
• Ko, S., Cho, S. G., Kim, D. and Cui, J., 2009, Modal Identification of Cabinets of Nuclear Power Plant Based on Experimental Study, Proceedings of the 35th KSCE Annual Conference, pp. 826~829.
• Tran, T.-T., Cao, A.-T., Nguyen, T.-H.-X. and Kim, D., 2019, Fragility Assessment for Electric Cabinet in Nuclear Power Plant using Response Surface Methodology, Nuclear Engineering and Technology, Vol. 51, No. 3, pp. 894~903. [https://doi.org/10.1016/j.net.2018.12.025]
• Eem, S., Lee, S., Choi, I.-K. and Chang S.-J., 2019, Experimental Study on the In-cabinet Response Spectrum Amplification Factor of Electrical Cabinets due to the High Frequency Earthquake, Proceedings of the 25th International Conference on Structural Mechanics in Reactor Technology.
• Electric Power Research Institute (EPRI), 2008, Guidelines for Development of In-cabinet Amplified Response Spectra for Electrical Benchboards and Panels, Technical Report No. EPRI-NP-7146-M.
• Yang, J., Rustogi, S. K. and Gupta, A., 2003, Rocking Stiffness of Mounting Arrangements in Electrical Cabinets and Control Panels, Nuclear Engineering and Design, Vol. 219, No. 2, pp. 127~141. [https://doi.org/10.1016/S0029-5493(02)00279-0]
• Rustogi, S. and Gupta, A., 2004, Modeling the Dynamic Behavior of Electrical Cabinets and Control Panels: Experimental and Analytical Results, Journal of Structural Engineering, Vol. 130, No. 3, pp. 511~519. [https://doi.org/10.1061/(ASCE)0733-9445(2004)130:3(511)]
• Han, M., Cho, S.-G., Hong, K.-J. and Gupta, A., 2018, Rocking Stiffness of Electric Cabinet Considering the Local Deformation at the Base, Transactions of the Korean Nuclear Society Spring Meeting.
• Yun, D.-W., Jeon, B.-G., Jung, W.-Y., Chang, S.-J. and Shin, Y.-J., 2019, Analysis of Anchorage Behavior Characteristics of the Electrical Cabinet using Shaking Table Tests, Transactions of the Korean Society for Noise and Vibration Engineering, Vol. 29, No. 1, pp. 43~50. [https://doi.org/10.5050/KSNVE.2019.29.1.043]
• American Concrete Institute (ACI), 2007, Qualification of Post-installed Mechanical Anchors in Concrete and Commentary, ACI 355.2-07.
• Lee, S. and Jung, W., 2021, Evaluation of Structural Performance of Post-Installed Anchors Embedded in Cracked Concrete in Power Plant Facilities, Applied Sciences, Vol. 11, No. 8, p. 3488. [https://doi.org/10.3390/app11083488]
• Rivera-Rosarino, H. T. and Powell, J. S., 2017, Installation Torque Tables for Noncritical Applications, NASA Technical Reports Server (NTRS) GRC-E-DAA-TN37585, NASA/TM-2017-219475, E-19347.
• The Institute of Electrical and Electronics Engineers (IEEE), 2013, IEEE Standard for Seismic Qualification of Equipment for Nuclear Power Generating Stations, IEEE Std 344-2013.
• The Institute of Electrical and Electronics Engineers (IEEE), 2018, IEEE Recommended Practice for Seismic Design of Substations, IEEE Std 693-2018.
• Ciurlanti, J., Bianchi, S., Pürgstaller, A., Gallo, P. Q., Bergmeister, K. and Pampanin, S., 2022, Shake Table Tests of Concrete Anchors for Non-structural Components Including Innovative and Alternative Anchorage Detailing, Bulletin of Earthquake Engineering, Vol. 20, No. 8, pp. 3971~3993. [https://doi.org/10.1007/s10518-022-01359-2]